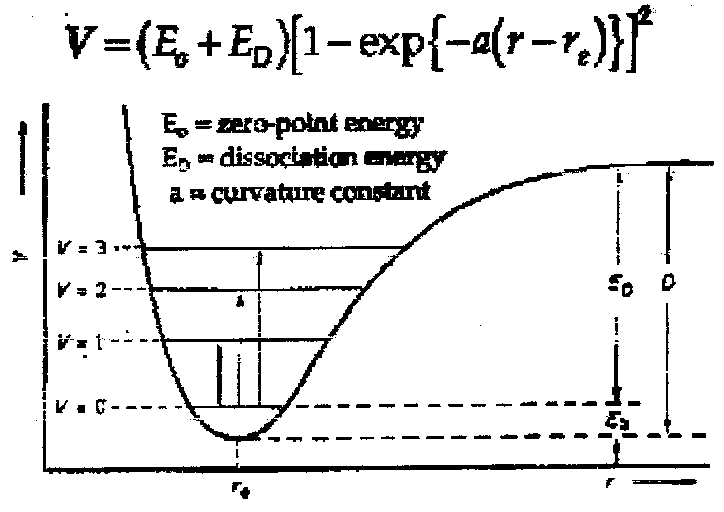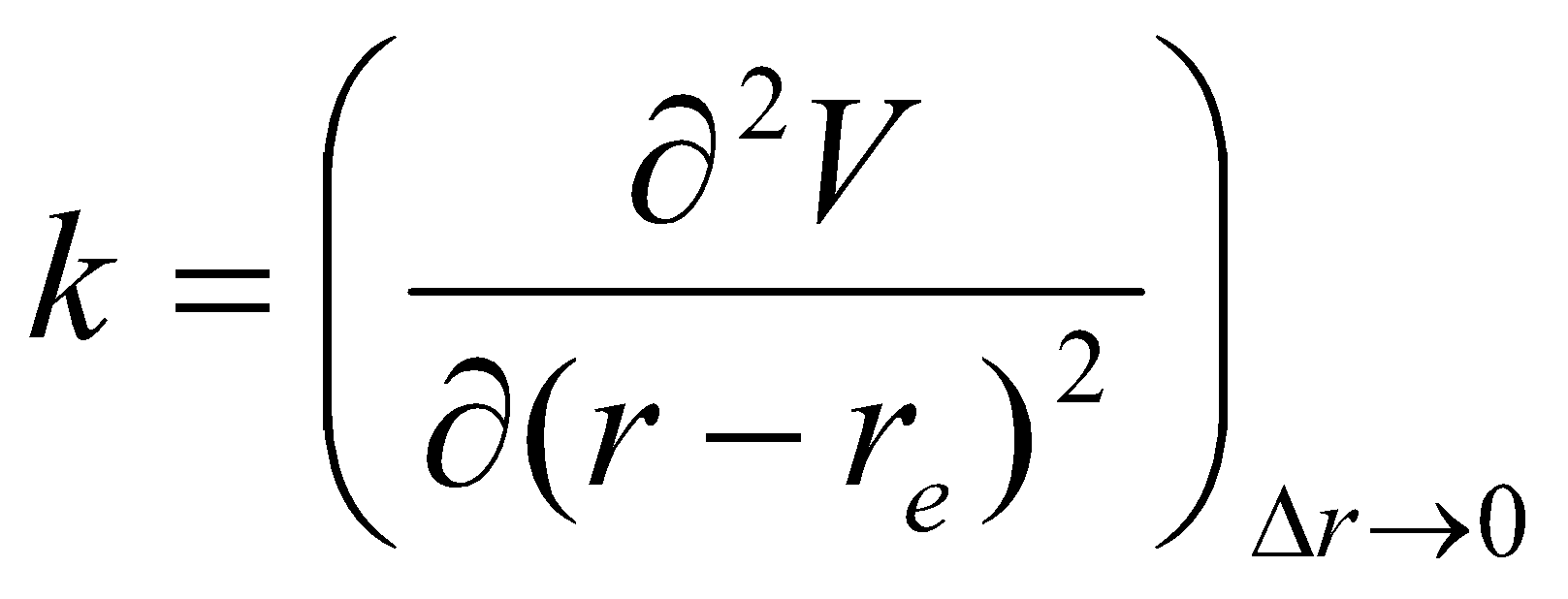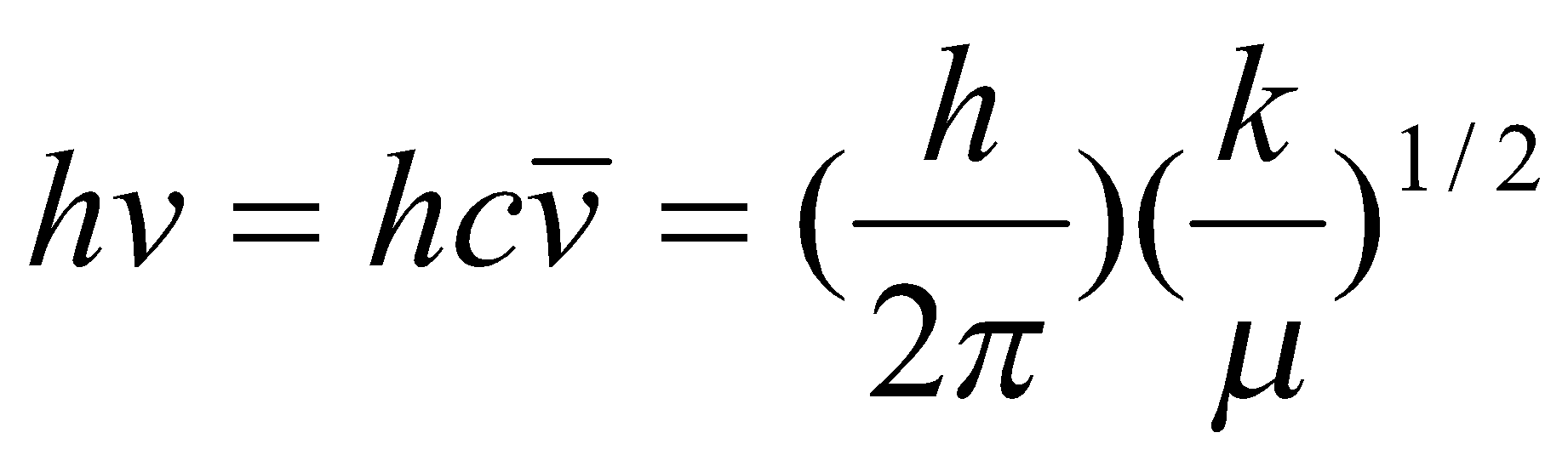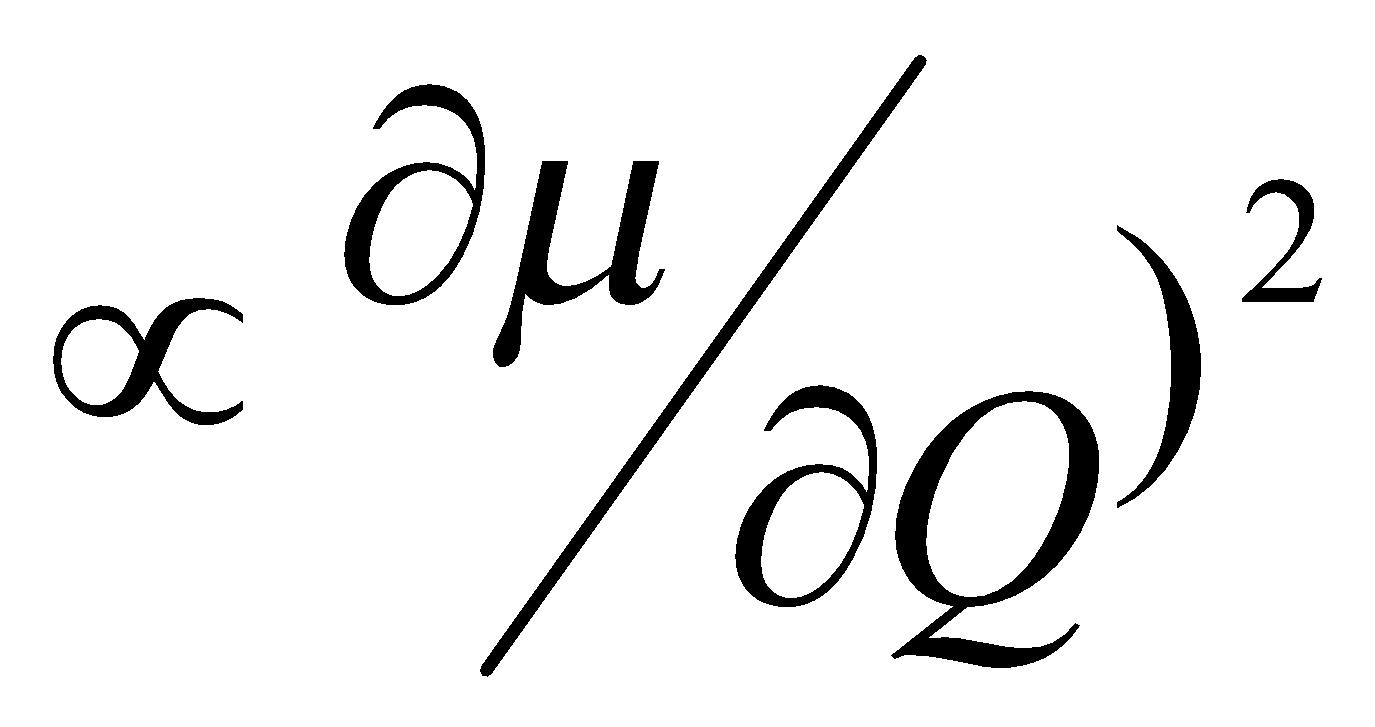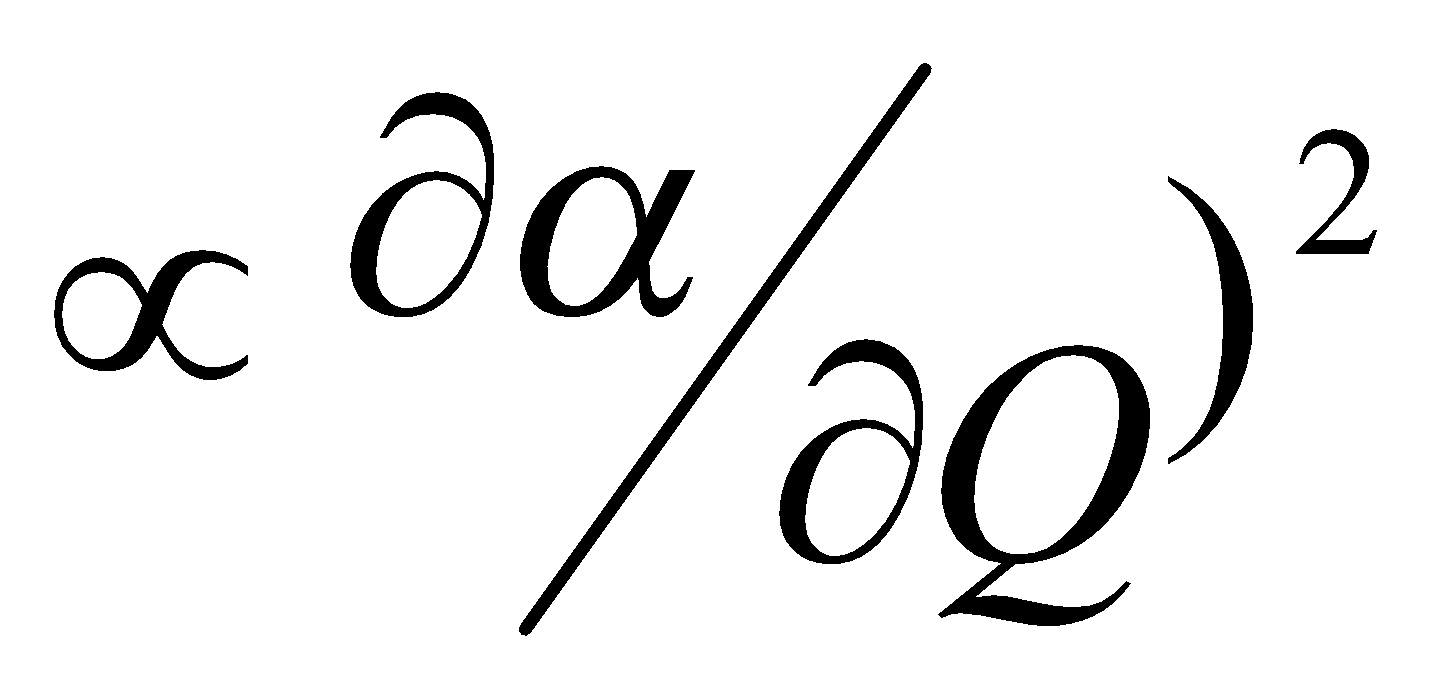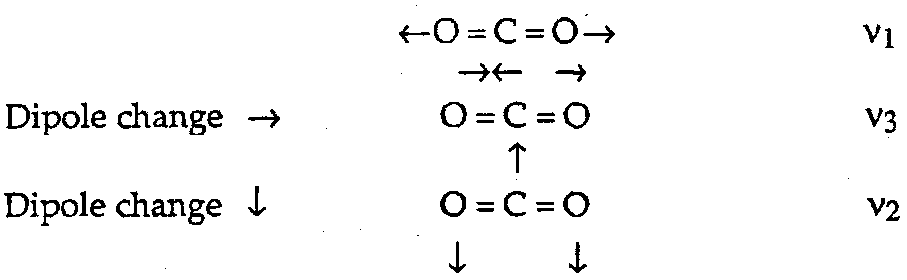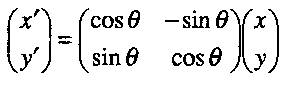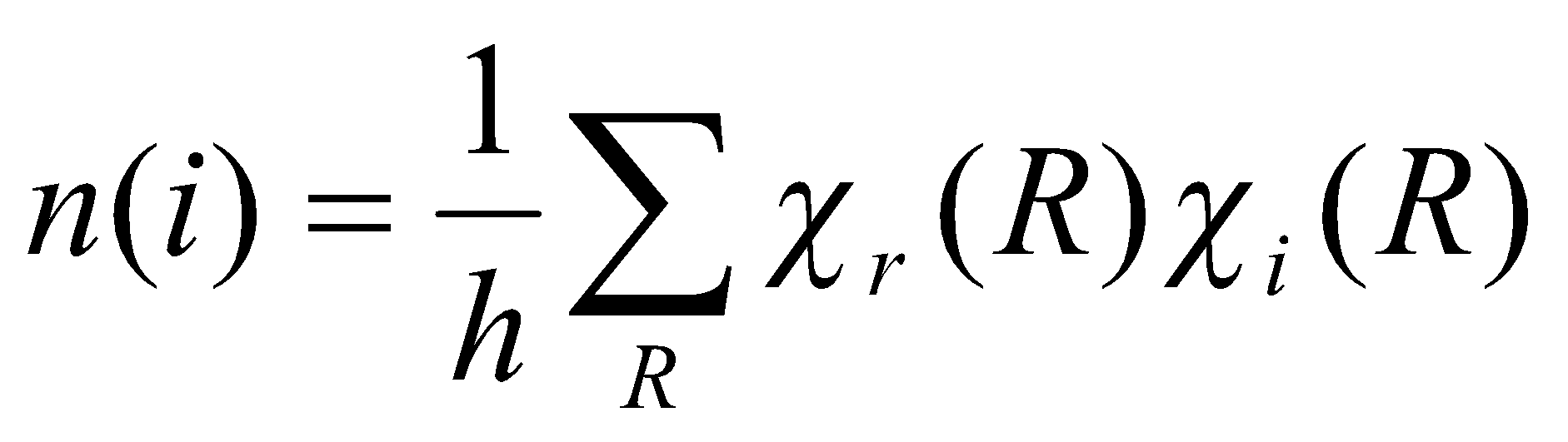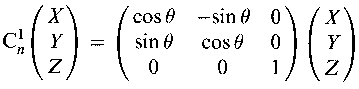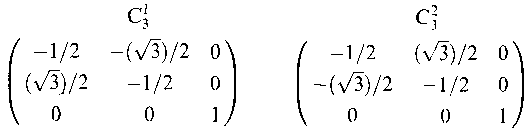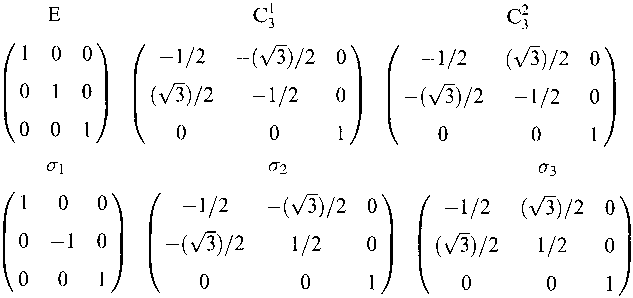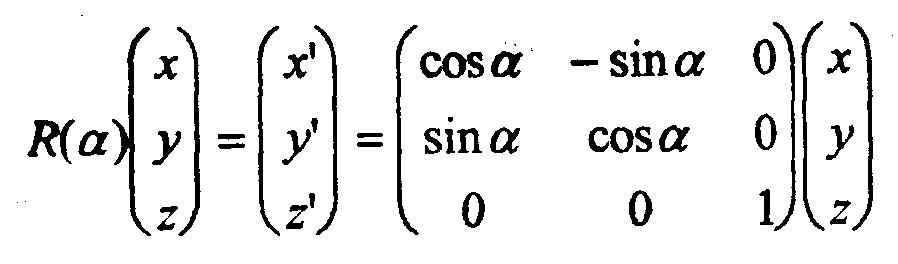Vibrational Spectroscopy Notes

(GROUP THEORY APPLICATIONS AT THE END)

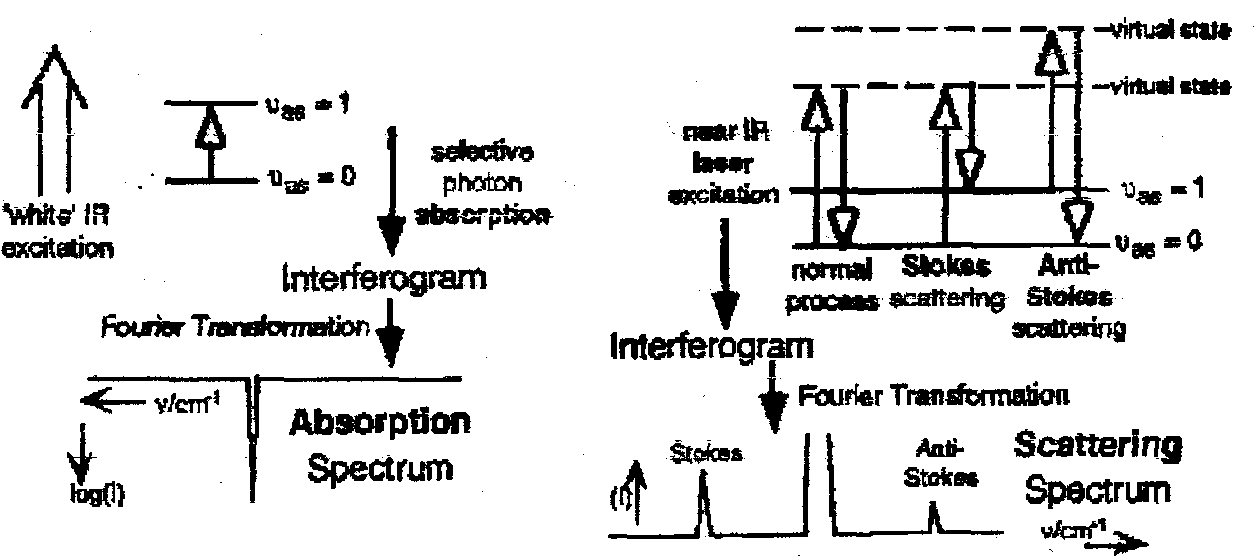
By the methods of vibrational spectroscopy we normally mean Infrared Absorption and Raman Scattering studies.

These involve quite different mechanisms of engineering vibrational transitions. Taken together, they are one of the three principal methods now used to characterise chemical compounds, along with X-ray crystallography and NMR Spectroscopy.

What Are Molecular Vibrations?

Consider atoms as masses connected by springs, so the restoring force, F = -kΔr, where k is the force constant of the spring (bond).

The motion is modelled by an Anharmonic Potential (modification of SHO):

The Morse Potential –

From a quantum mechanical treatment, this gives rise to energy levels, Ev = hv(ν+½), v = 0,1,2 …

Or more precisely Ev = hv [ (ν+½) - x(ν+½)2] to correct for anharmonicity, where:

v = characteristic fundamental vibrational frequency.

ν = vibrational quantum number which distinguishes vibrational levels.

x = characteristic anharmonicity constant (for real molecules, x > 0).

The force constant is:

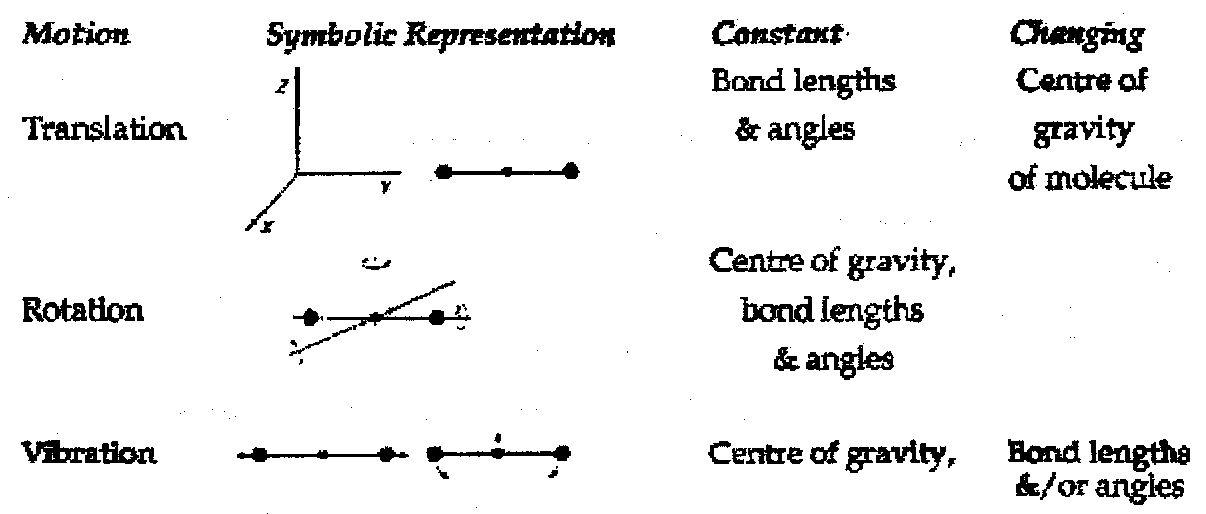
Fundamental (Normal) Modes of Vibration

All vibrations may be described as a linear combination of fundamental modes.

Fundamental Modes of vibration are defined by the following conditions –

1. All atoms of the molecule move with the same frequency and usually in-phase i.e. all pass zero crossings and turning points at the same time. Amplitudes, however, depend on masses.
2. Fundamental vibrational modes do not cause translation or rotation of the molecule as a whole.
3. Each fundamental mode can be excited independently.
4. Modes are not usually localised at a single bond, but include several atoms. The vibrational Normal Coordination, Q, derived from masses and relative atom movements involved, replaces the simple coordinate (r-re).

Classification of Fundamental (Normal) Modes

Ease of Vibration:

Typically Force Constants (and so Vibrational Frequency) ν > δ > γ > τ.

Symmetric (s) – symmetry of molecule is retained throughout vibration.

Asymmetric (as) – one or more symmetry elements vanishes during vibration.

The vibrational spectrum will not necessarily contain the same number of bands as there are fundamental modes, for several reasons:

• Combination bands (i.e. v1 + v2)
• Overtone bands (2v1)
• Vibrations may be degenerate
• Vibrations may be inactive
• Intensities may be too low
• Vibration might be outside the range of the machine

Typical Energies / Frequencies / Wavenumbers / Wavelengths

Fall in the mid-IR region of the electromagnetic spectrum. This is due to the typical values of the force constants and atomic masses, as:

ΔE =

The force constants relate to bond order and bond polarity.

• A larger force constant is often interpreted as indicating a stronger bond, but there is no direct relationship between bond dissociation energy and force constant.
• Clearly force constants are a better measure of bond strength than are vibrational frequencies, because latter are influenced by atomic mass.
• For complex molecules, force constants for a bond cannot be simply related to the frequency of a given fundamental band. They must be obtained by normal coordinate analysis.

IR Spectroscopy                               cf.                         Raman Spectroscopy

• Polychromatic excitation
• Absorption
• Absolute Frequencies (high v resolution)
• Resonant Technique
• Strong effect → sensitive

• Monochromatic excitation
• Scattering
• Frequency difference (low resolution)
• Non-resonant technique
• Weak effect → insensitive

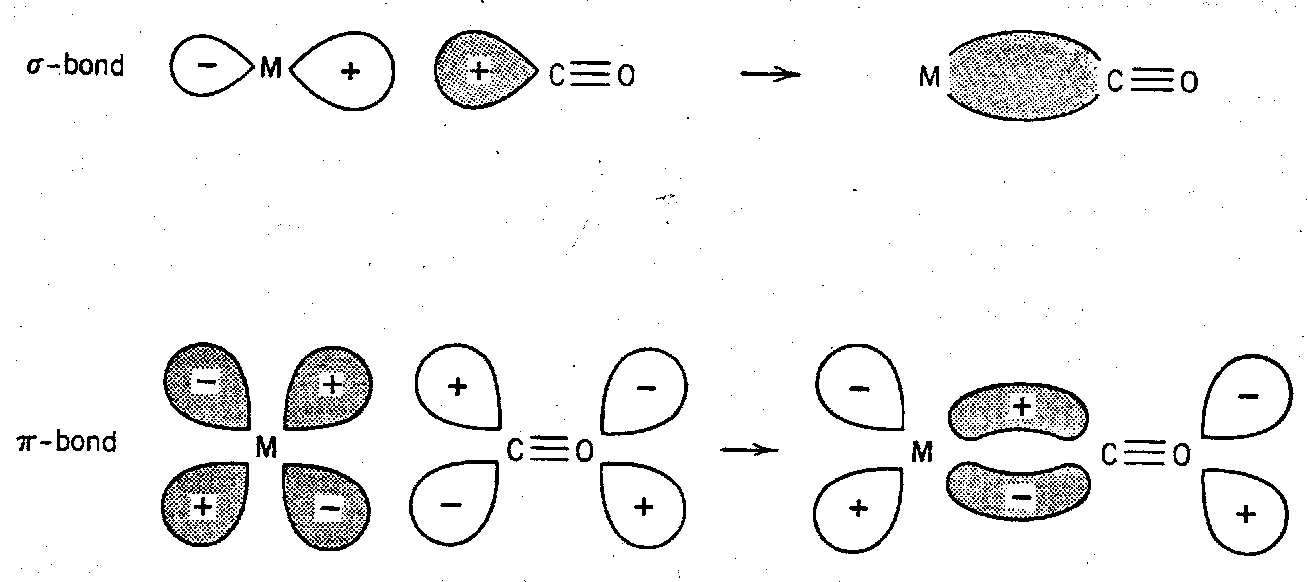
Interaction of Vibration and Photon through interaction of the oscillating electric dipole vector of the electromagnetic radiation with:

Oscillating Molecular Dipole

dμ/dQ ≠ 0

Polarisation of Electron Cloud

dα/dQ ≠ 0

Fundamental vibrational mode must belong to one of the irreducible representations corresponding to:

Electric Dipole Operator

(x,y,z – vector components)

Polarisability Operator

(x2, y2, z2, xy, xz, yz and combinations – tensor components)

Hence they are both complementary techniques, and can measure different vibrations (e.g. centrosymmetric molecules show Mutual Exclusion)

	Intensity
Water absorbs strongly	Solvents	Water scatters weakly
Alkali halide needed	Windows	Glass OK

Other Sources of Vibrational Spectroscopy –

• Inelastic Neutron Scattering         –         no selection rules
• Electronic Spectroscopy                 –         vibrational fine structure of excited states.
• UV Photoelectron Spectroscopy         –         vibrational fine structure of ions.

Use of Symmetry Considerations to assign IR/Raman Spectra

(SEE END FOR MORE ON SYMMETRY)

The fundamental infrared and Raman bands of XeOF4 were determined from measurements on the gas and liquid respectively. Show that the molecule is square pyramidal, by assigning the fundamentals.

Two Raman bands, one at 230cm-1, the other near 608cm-1, were expected but not observed. Infrared measurements were not made below 200cm-1.

Assignment Aids:

• IR / Raman Activity
• Raman Bands of totally symmetric modes are Polarised (P).
• Typical frequencies: Stretches > In-plane bending > out-of-plane bending.
• Look for the symmetry elements that are conserved in a vibrational mode.

Functional Group Identification – “Fingerprinting”

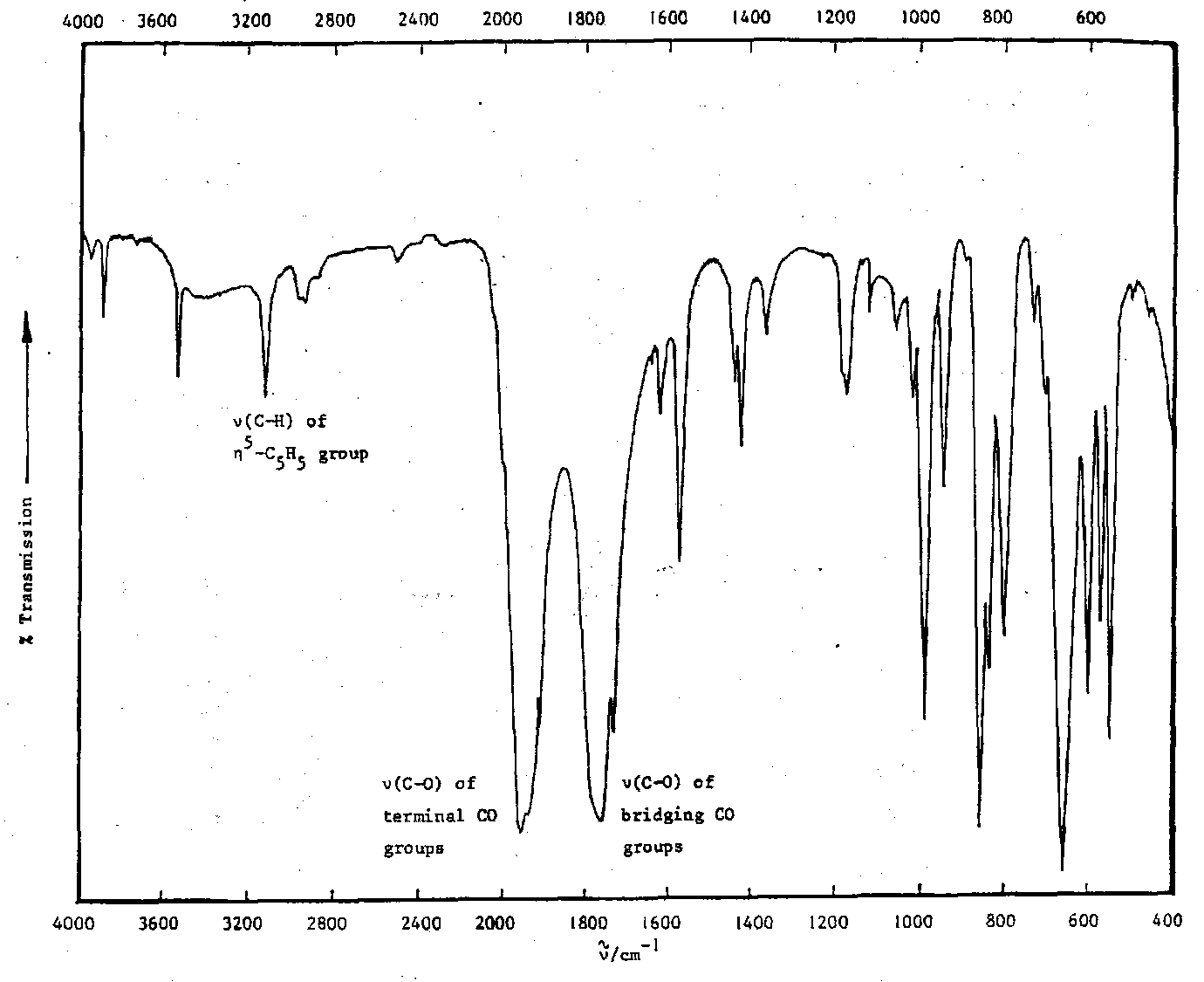
• Some groups give rise to distinctive frequencies no matter what molecule they are incorporated into, e.g. C=O stretch in metal carbonyls.

Terminal = 1850-2125cm-1

Bridging = 1700-1860cm-1 (weaker due to backbonding)

• Fundamental associated with a specific group may be identified by their characteristic solvent variations.
• When the group vibration approach fails the most likely reason is Coupling and then the full vibrational analysis approach must be performed.
• Successful Group Vibrational analysis is typically with v > 1200cm-1. Vibrations with v < 1200cm-1 typically involve large parts of the molecule.
• Comparison with standard spectra allows identification of substances. Especially useful for more complex molecules with overlapping group vibrations.
• Identifies impurities (especially IR which is very sensitive).

Structure and Geometry Determination

Analysis of IR / Raman activity may elucidate the geometry of a molecule.

Metal-Metal bonds are often detected from low frequency M-M stretches in Raman Spectra, e.g. Hg22+ from Raman band at 169cm-1.

Reaction Analysis

Both IR and Raman may be quantified using modern instruments. Absorbance is indicated from the Beer-Lambert Law:

Absorbance, A = εcl = log10(Io/I)

Determine Equilibrium Constants:

Raman spectrum quantifies amounts of each species.

Determine Rates:

IR spectrum detects changes in stretches – monitor isomerisation.

Isotopic Substitution

Isotopic substitution alters vibrational frequencies. The force constant k remains constant, but mass has changed.

Isotopic substitution can dramatically indicate structure:

e.g. A1 NSi3 stretch in N(SiH3)3 invariant to 14/15N exchange → trigonal planar.

A1 NC3 stretch in N(CH3)3 changes with 14/15N exchange → pyramidal.

e.g. (NH3)3Ru(N2)2+ with 15N14N shows doublet form in N-N stretch. Indicates end-on binding of N2.

(Ph3P)2Pt(O2) with 16O18O shows only a single O-O stretch – indicates side-on binding of O2.

Isotope perturbation is usually essential to generate enough data to avoid normal coordinate analysis of molecules being an under-determined problem. This works because isotope perturbation changes frequencies, but, to a good approximation, not the force constants.

Fast Timescale

≈ 1014s → usually a rigid picture of molecules.

Different Environments

Gases

Low pressure / diatomics and triatomics – rotational fine structure.

Liquids / Solutions

Broadening due to random differences in local environment – no fine structure.

Crystals

Sharp lines due to regular environments – no rotation.

Polarised light directed at single crystals – dichroic effects.

Matrix Isolation

Dilute dispersion in an inert matrix at low temperature.

Excellent resolution spectra due to quenching of rotation, especially good for discerning small isotope effects.

Preparation and characterisation of unfamiliar and/or unstable molecules.

Extreme Conditions

Catalytic cycles can be studied under extreme pressure / temperature etc.

Sensitivity of IR detects small equilibrium quantities of intermediates.

Applications and Examples

With reference to the vibrational spectrum of a compound we can typically achieve the following:

1. Detection and identification of a known compound (“fingerprinting”; tests of purity).
2. Working out the constitution of an unknown compound (presence of functional groups, e.g. Cp and CO).
3. Monitoring of chemical changes.
4. Determining the concentration of a compound (Quantitative analysis, e.g. kinetic studies involving metal carbonyls).
5. Likely structure of a molecule (use of Selection Rules and isotopic effects).
6. Normal coordinate analysis to determine the force constants of a molecule. Problems of bonding (e.g. B2H6).
7. Polarisation measurements to determine supplementary information about molecular symmetry (e.g. in Raman) and also to study single crystals (e.g. CaCO3).

Four Examples

1) Fe(CO)5 + [C5H6]2 → ‘(C5H5)Fe(CO)2’                yellow-brown solid

The IR spectrum of the solid shows the presence:

1. of an ~n5-C5H5 group (band near  3100cm-1) and
2. two types of CO group. Molecule is a dimer. Possibility of isomerism?

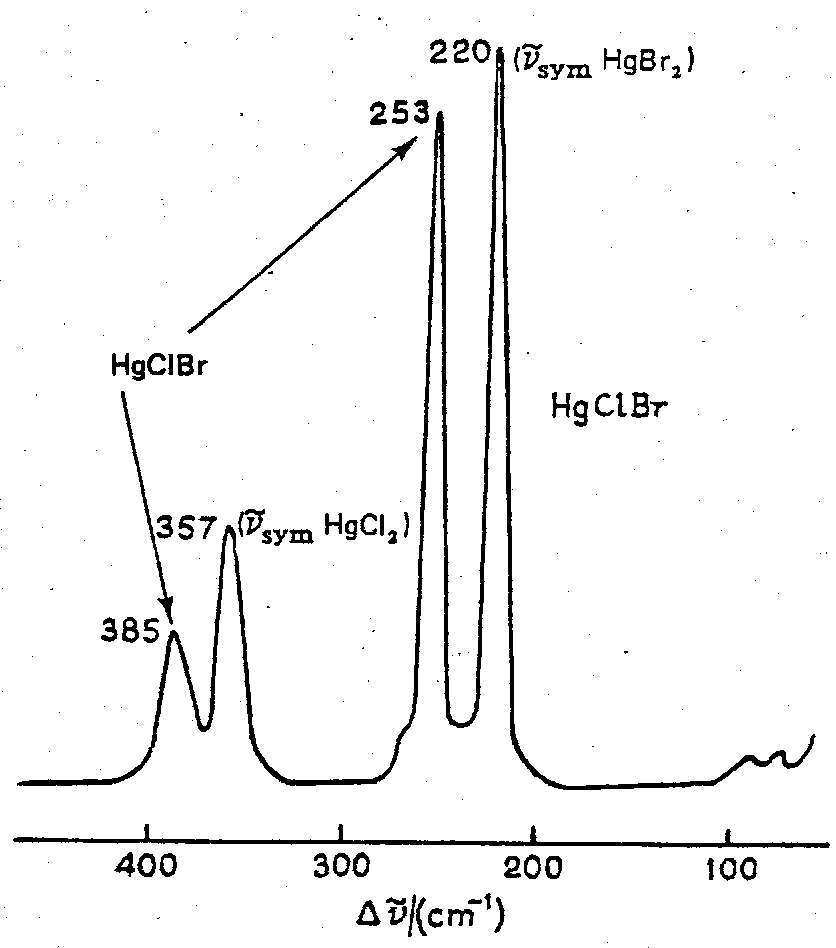
2) Cl-Hg-Cl + Br-Hg-Br ⇌ 2Cl-Hg-Br                Raman spectrum of the vapour.

The spectrum of the mixed vapour shows two new bands due to the formation of the mixed halide Cl-Hg-Br. The results can be used to determine the equilibrium constant, K, for the reaction and, by exploring how K varies with temperature, the enthalpy change of the reaction can also be determined.

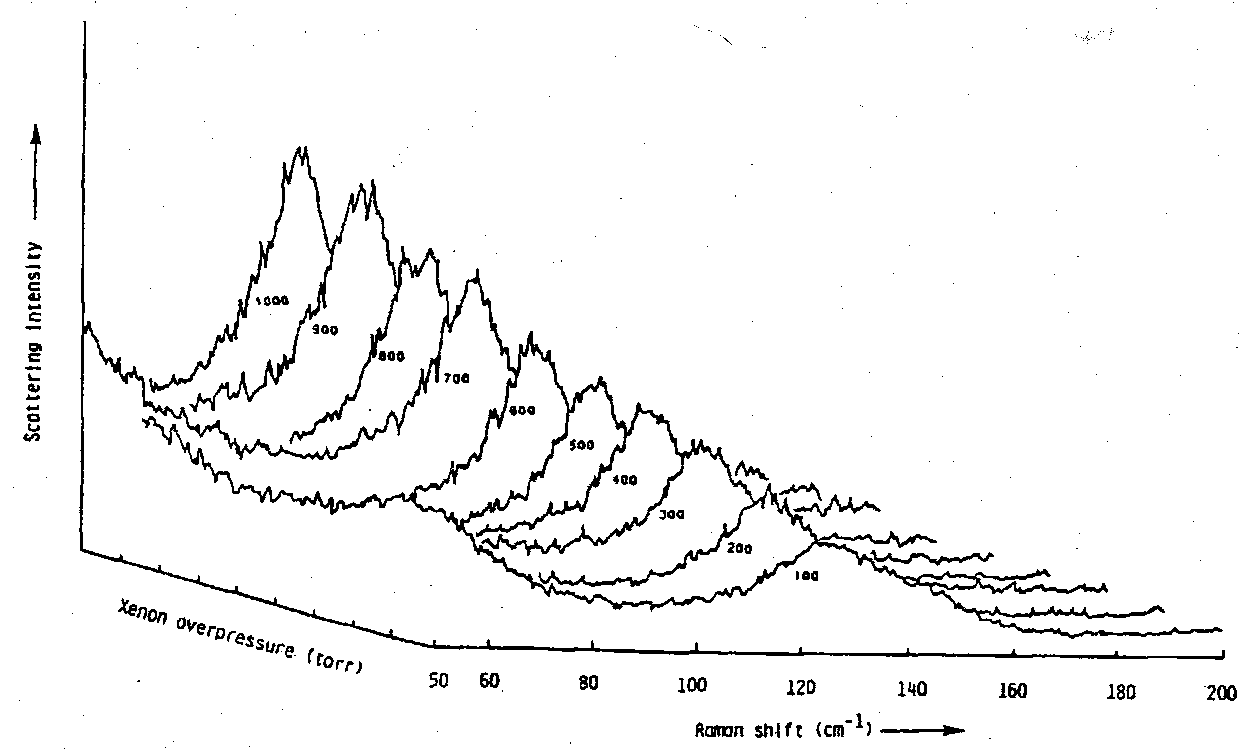
3) XeF+Sb2F11- ⇌ Xe2+        SbF5 solution

The Raman Spectrum of the solution shows a new band at 123cm-1 which grows when the over-pressure of xenon increases. This is due to the formation of Xe2+. Note the extent of formation of Xe2+ and the dependence of the intensity of the band on the xenon pressure.

4) Al atoms co-condense with CO to form Al(CO)x

The IR spectrum of the deposit indicates the formation of an aluminium carbonyl, Al(CO)x. By the use of a mixture of C16O and C18O, we can show that x=2 [giving a bent molecule].

Study of Vibrational Transitions

Vibrational transitions are characterised typically by the following parameters:

Frequency = 1013-1014Hz

Wavenumber = 102-103cm-1

Energy = 1-10kJ

cf. RT = 208cm-1 at 298K

The transitions may be studied by the following methods:

• Infrared Absorption
• Raman Scattering
• Electronic Spectra

1. Absorption – vibrations of electronic excited state.
2. Emission – vibrations of electronic ground state.

• Inelastic Neutron / Electron Scattering

• Photoelectron Spectra – molecular ions.

Characteristics of Vibrational Spectrum

For each band in a given vibrational spectrum we should be concerned with three properties:

1. Position – frequency – wavenumber – energy.

Wavenumber = function of force constants, masses of atoms, geometry of molecule.

2. Intensity – depends on rate of change of dipole moment, μ, or induced dipole moment, π, with respect to the normal coordinate, q, i.e. dX/dq may be zero.

Depends on molecule symmetry. Selection Rules.

3. Shape – effects of molecular rotation, intermolecular forces, and isotopic changes.

Born-Oppenheimer Approximation

The factorisation implied by this is based on very different magnitudes of the energy changes, where electronic >> vibrational >> rotational, normally.

However, there are some significant exceptions, for example:

1. d-d electronic transitions of an octahedral transition-metal complex – antisymmetric vibrations relax the strict electronic selection rules forbidding transitions between g states.
2. Jahn-Teller phenomena.
3. Coupling rotational and vibrational motions – Coriolis and Centrifugal effects.

Rotational Spectra

Pure rotational transitions in a molecule can be induced by radiation in the far infrared and microwave regions of the spectrum. They can also be induced in the Raman effect. Extremely high precision for frequency determination is possible in the microwave region. Compared with the infrared region of the spectrum, where measurements are routinely made to about 1 cm-1, a resolution of the order of 10-8 cm-1 may be achieved in the microwave region. A wide spectral range plus resolution and accuracy offers impressive opportunities for fingerprinting, particularly of molecules in space.

There are four requirements that limit microwave studies:

• The material must be in the gaseous state. For conventional instrumentation a vapour pressure of > 10-3 Torr is needed.
• The molecule must have a permanent electric dipole moment in the ground state in order to absorb microwave radiation.
• Transitions are subject to the selection rule ΔJ = ±1.
• For useful structural studies, the molecule needs to be comparatively simple one.

Some of the most accurate molecular dimensions come from microwave and related studies.

The moments of inertia (the number of which varies depending on the shape of the molecule – spherical top – IA = IB = IC, oblate symmetric top = IA = IB ≠ IC etc.) are related to the bond lengths and angles of the molecule, and a whole series of simultaneous equations has to be solved to determine all the structural parameters. Note that for a given molecules no more than three independent items of structural information (IA, IB and IC) can be determined. It is often necessary to carry out the microwave spectrum measurements of isotopically different version of the molecule to generate enough information to solve.

• Intensities – because the general rotational level with quantum number J has a degeneracy of (2J+1), the populations of the levels increase as 2J+1, and so do the intensities of the transitions. Counteracting this increase, however, is the Boltzmann Factor for populations. In addition, the various levels may have different statistical weights because of the interaction of the nuclear spins of the atoms making up the molecule with the overall angular momentum.
• The Stark Effect – accurate dipole moment measurements can be made in microwave experiments by examining the Stark Effect. When an electric field is applied to the sample, the rotational lines are split to an extent depending on the dipole moment of the molecule which can thus evaluated.
• Rotational Raman Spectra. Rotational transitions of some simple gaseous molecules without a permanent dipole moment can be observed through the Raman Effect. This is the case, for example, with H2, N2, F2 etc. For a diatomic molecule the selection rule ΔJ = ± 2 now applies and the frequency separation between the lines is 4B (cf. 2B in microwave studies).

Rovibrational Spectra

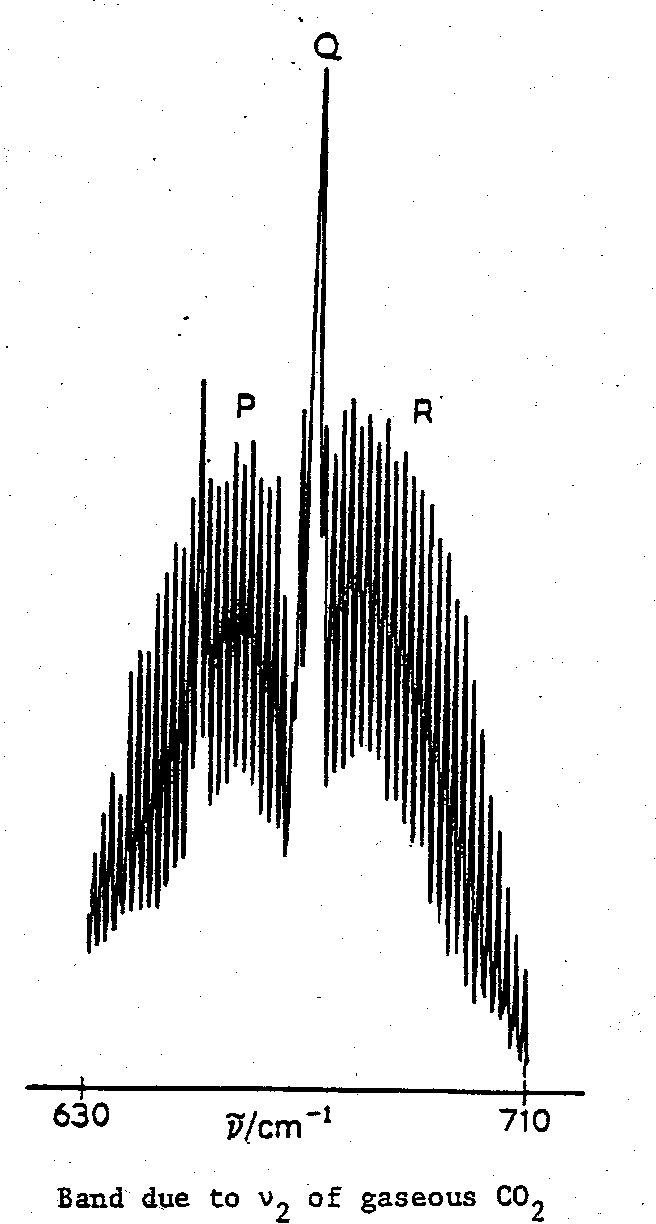
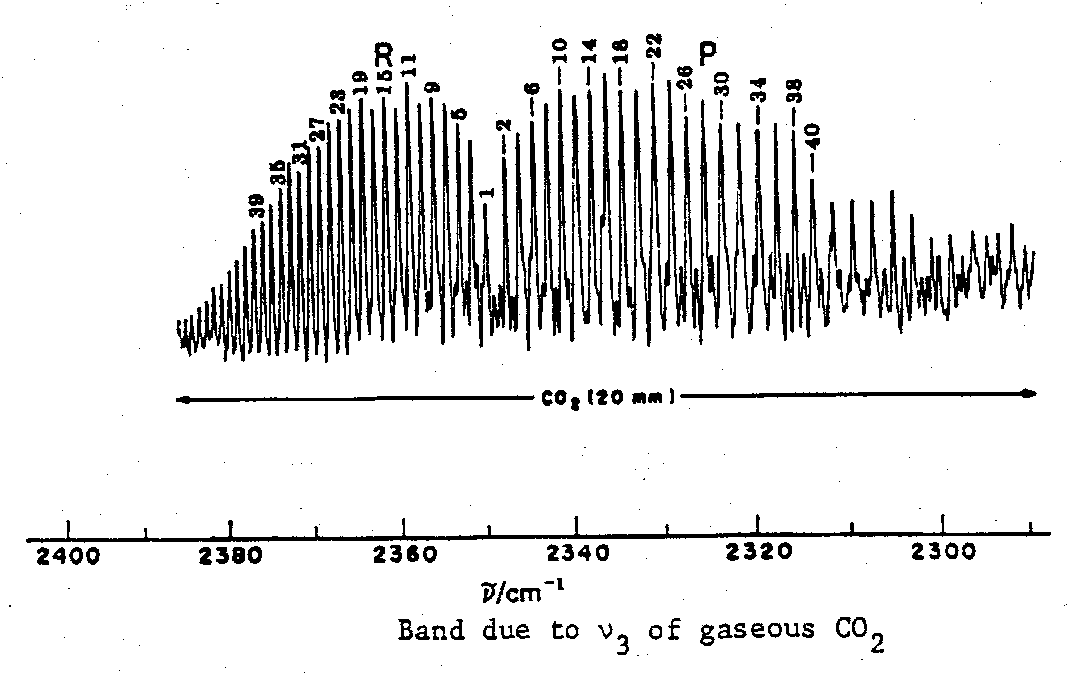
Here we consider a simple gaseous molecule like CO2 and the infrared absorption associated with a particular vibrational transition.

Then the band will be expected to exhibit fine structure corresponding to rotational transitions, typically grouped in so-called P, Q and R branches, as follows:

Note that what we observe depends on:

1. the type of vibrational transition – in relation to the symmetry of the molecule.
2. The type of rotor (e.g. spherical top, symmetric top, etc)
3. The magnitudes of the moments of inertia.

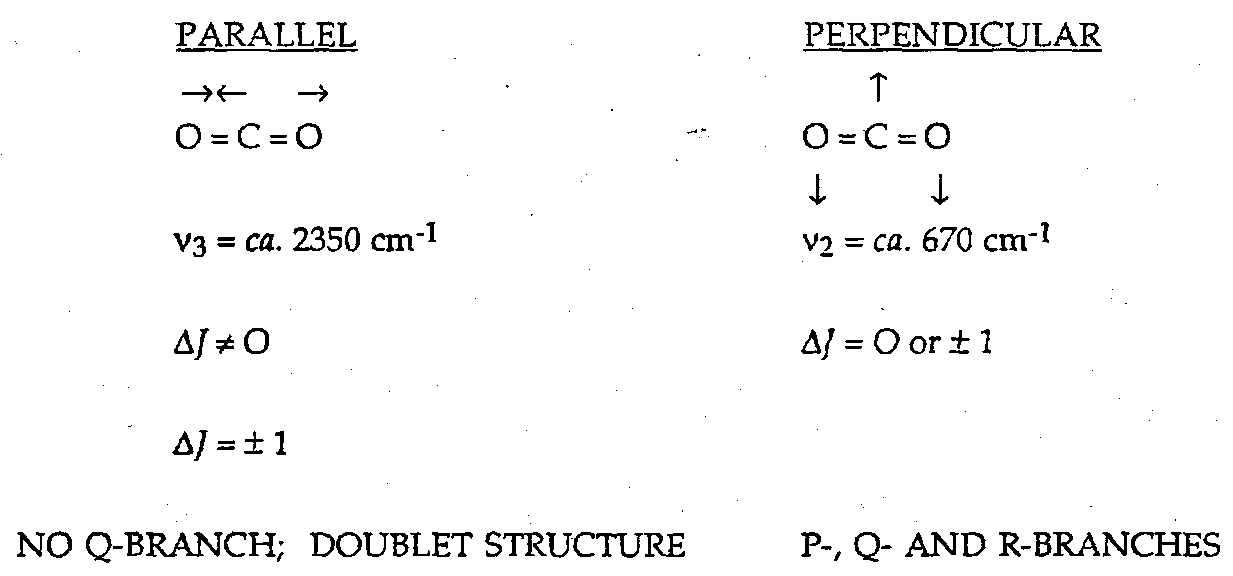
For a linear molecule like CO2 we can distinguish between vibrations with a dipole change which is parallel and those with a dipole change which is perpendicular to the principal axis of the molecule.

The separation between the individual rotational lines tells us about:

1. the moments of inertia of the molecule (but these differ slightly with the vibrational state of the molecule)
2. coupling between the vibrational and rotational motion of the molecule – Coriolis and Centrifugal effects.

The envelope of the band reflects the population of the rotational levels, and the separation between the maxima of the P and R branches is a function of (i) the moments of inertia of the molecule, and (ii) the temperature.

As the moment or moments of inertia of the molecule increase, the rotational lines crowd closer and closer together, and ultimately cannot be resolved. Nevertheless, the envelope may still show a distinctive shape.

Such observations indicate a molecule with small-to-medium moments of inertia (one of which may be estimated roughly from P-R branch separation in favourable cases).

What is also important to the spectroscopist is that the shape of the band gives a clue to direction of the dipole change associated with a vibration, e.g. O=C=S. Hence we may be able to identify which vibrational transition is which. However, as the moments of inertia become larger and larger, even this evidence of the rotational transitions is finally lost, and the vibrational band assumes a featureless contour.

Condensed Phases

In the solid or liquid phases, compounds show vibrational spectra reflecting the following properties:

1. Rotation of molecules is usually wholly or partially quenched, and we see only features attributable to vibrational transitions.
2. Intermolecular forces broaden the vibrational levels of the molecules and so may result in quite broad infrared and Raman bands.

Matrix Isolation seeks to avoid the problems of broadening due to intermolecular forces by trapping the molecules in a solid, inert support such as a solid noble gas or nitrogen. Hence very sharp vibrational bands may be observed.

Energy of Vibrational Transitions

Here we are concerned with a fundamental transition between the v = 0 and v = 1 vibrational states.

We need to define a normal coordinate q in terms of which we can express the kinetic and potential energies of the vibrating molecule. Initially we consider the case of a diatomic molecule and take stock of the magnitude of anharmonicity terms. We then move on to the more general secular equation for a polyatomic molecule vibrating with SHM and find that we have a polynomial in the vibrational frequencies of the order 3N-6. Hence we seek to determine the force constants of the molecule.

Meaning of the Stretching Force Constants

A force constant measures d2V/dr2, i.e. the curvature at the foot of the potential well.

The values of the force constant reflect:

• Bond Polarity
• Bond Order

Consider two examples:

1) Metal Carbonyls

Take the case of three isoelectronic metal tetracarbonyls (all with Td symmetry):

Force Constant	Ni(CO)4	Co(CO)4-	Fe(CO)42-
fCO /Nm-1	1628	1322	1140
fMC /Nm-1	249	355	406

For free CO fCO = 1860cm-1. These figures display more convincingly than almost any other piece of evidence the two-way action we believe to be essential to the bonding of transition metal carbonyls. Note that, as the negative charge builds up on the metal, so the degree of π-backbonding increases, reducing the bond order of the CO group, while enhancing that of the M-C group. But what about the effects of σ-donation on the CO groups? What is the significance of the finding that fCO = 1860cm-1 and 1940cm-1 for CO and CO+ respectively?

2) PF5

Bond	Force Constant /Nm-1	Length /pm
P-Fax	440	158.0
P-Feq	620	153.2

The different characters of the axial and equatorial bonds are strongly in evidence in the force constants, whereas the bonds differ only slightly in length.

Intensities and Selection Rules

Here we are concerned with:

1. the symmetry classification of the 3N-6 normal coordinates (normal modes or vibrational eigenfunctions), to be exemplified by the case of a tetrahedral MX4 molecule.
2. The activity of the relevant modes in infrared absorption or Raman scattering (Selection Rules)
3. Polarisation experiments in which specific components of the dipole moment derivative or induced dipole moment derivative are excited by the use of plane polarised radiation in the infrared or Raman experiments.

Nature of the Problem

The probability of a spectroscopic transition is given by the Transition Moment:

This relates to a transition between an initial state defined by the time-independent vibrational eigenfunction ψk and a final state defined by the time-independent vibrational eigenfunction ψl. X is the dipole moment operator for infrared absorption or the polarisability operator for Raman scattering, and dτ is a volume element. In classical terms there must be a change of dipole moment for a vibrational transition to be active in infrared absorption, and a change of polarisability for a vibrational transition to be active in Raman scattering. In quantum mechanical terms we have to ensure that the Transition Moment is non-zero.

This in turn requires that the integrand contains the totally symmetric representation of the relevant molecular point group, a condition which can be meet only if X and ψk and ψl separately contain the same irreducible representation.

Symmetry And Group Theory

Symmetry Operations

Cn – rotation by 360o/n about an axis. It is a proper symmetry operations (can be realised).

σ – reflect in a plane. It is an improper symmetry operations (cannot be physically realised).

i – invert through a centre. It is improper.

Sn – rotate by 360o/n, then reflect in a plane perpendicular to the rotation axis. Improper, due to σ component.

E – the identity. Do nothing.

Symmetry Elements –

These are the axes, planes and centres for the above operations.

For Cn and Sn operations, n > 2  means there are addition symmetry operations, e.g. C32 (the combined effects of 2 C3 operations).

Note that:

σ2 = i2 = C22 = C33 = Cnn = E.

C42 = S42 = C2.

Chirality –

A molecule is chiral if it cannot be superimposed on its mirror image. Any improper symmetry operation generates a mirror image, and so:

A molecule is chiral if, and only if, it has no improper symmetry elements.

e.g. CH2ClBr has a reflection plane and is therefore not chiral. CHFClBr has no reflection plane, centre of inversion or Sn axis, and is chiral.

Point Groups

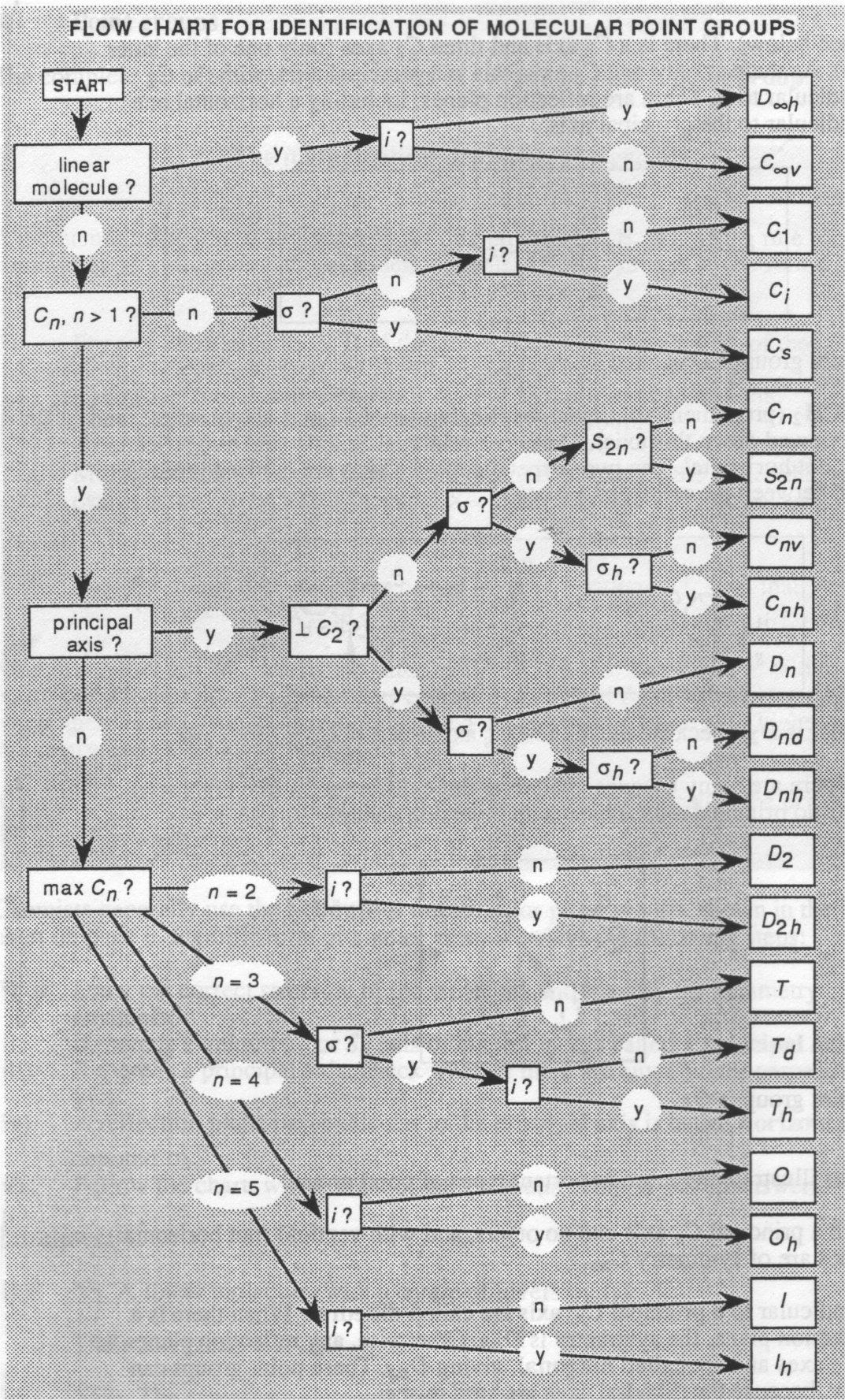
Chemists generally use the Schonflies Notation for point groups. The identification of these point groups can be ascertain by following the flow chart below.

This involves the following steps:

1. Draw the correct structure of the molecule, and identify the symmetry elements.
2. If there is a unique Cn or Sn axis of highest n, it is called the principal axis.
3. If there is a principal axis, check whether there are any C2axes perpendicular to it.
4. A reflection plane perpendicular to the principal axis is called the horizontal, and denoted σh.
5. Follow the chart, answering yes/no!

In order to correctly assign the point group, the correct structure is needed (1). VSEPR Rules are useful to predicting unknown structures of simple molecules:

1. Electron pairs tend to minimise repulsions. Ideal geometries are:

1. Coordination Number 2 is linear.
2. Coordination Number 3 is trigonal.
3. Coordination Number 4 is tetrahedral.
4. Coordination Number 5 is trigonal bipyramidal.
5. Coordination Number 6 is octahedral.

2. Repulsions are of the order LP-LP > LP-BP > BP-BP.

1. When lone pairs are present, the bond angles are smaller than predicted by rule 1.
2. Lone pairs choose the largest site, e.g. equatorial in TBP.
3. If all sites are equal, lone pairs will be trans to each other.

3. Double bonds occupy more space than single bonds.
4. Bonding pairs to electronegative substituents occupy less space than those to more electropositive substituents.
5. If the central atom is in the third row or below in the periodic table, there are two possibilities:

1. If the substituents are oxygen atoms or halogens, the above rules apply.
2. If the substituents are less electronegative than halogens, the lone pair will occupy a non-bonding s orbital and the bonding will be through p orbitals and near 90o bond angles.

Note the similarity of the Point Groups –

All those molecules which have a perpendicular C2 to the principal axis are D (this stands for Dihedral).

If there is a subscript v, there is only a vertical reflection plane. If there is a subscript h, there is a horizontal reflection plane. If there is a subscript d, there is a reflection plane along the diagonal.

High symmetry molecules with no principal axes generate the T, O and I Point Groups. These are called cubic.

Consequences of Symmetry

Any physical property of a molecule cannot be altered by a symmetry operation. One such consequence is that any molecule with a non-zero dipole moment can have at most the following symmetry elements:

Single Cn axis.

Reflection planes containing that axis.

This fits only for the point groups C1, CS, Cn, Cnv, Cv

Any molecules with an inversion centre, a perpendicular plane or more than one axis do not have a dipole.

Classes

Two or more symmetry operations of a point group are placed in the same Class if they are related by other symmetry operations of the same group.

Two elements A & B of a group fall in the same class if there is some element C, such that:

C-1AC = B

This can be tested using Similarity Transformations. Some examples:

C31C31C3-1 = C31C31C32 = C31E = C31

AND

C32C31C3-2 = C32C31C31 = EC31 = C31

Therefore same class.

Similarly,

σ‘C31σ‘  = σ‘σ‘‘‘ = C32

σ‘‘C31σ‘‘ = σ‘‘σ‘ = C32

σ‘‘‘C31σ‘‘‘ = σ‘‘‘σ‘‘ = C32

Matrix Representations of Operations and Groups

Consider a rotation in the x,y plane.

The coordinates (x’,y’) after rotation can be expressed in terms of the original ones (x,y) as follows:

x’ = x cos θ – y sin θ

y’ = y sin θ + y sin θ

In matrix form:

In a similar way, for reflection in the y axis:

Thus, the above matrices represent the effects of the rotation and reflection, with the x,y coordinates as a basis.

Note that, as should be the case, σ 2 = E and σ = σ -1 .

A matrix representation of a group is a set of matrices with the same “multiplication table” as the group. That is, if symmetry operations A, B and C are represented by matrices M(A), M(B) and M(C) then if:

C= AB

We must have M(C) = M(A) M(B).

Consider the point group C2v with multiplication table:

	E	C2	σx	σy
E	E	C2	σx	σy
C2	C2	E	σy	σx
σx	σx	σy	E	C2
σy	σy	σx	C2	E

The first row of number below form a representation generated by the unchanged z coordinates as a basis, but the second is not a representation, as it does not conform to the multiplication table.

E	C2	σx	σy
1	1	1	1
2	0	1	1

It turns out that the only one dimensional representations possible are those shown below:

	E	C2	σx	σy
Γ1	1	1	1	1
Γ2	1	1	-1	-1
Γ3	1	-1	-1	1
Γ4	1	-1	1	-1

For C2v these are irreducible representations.

Character Tables

Group characters are the traces of the irreducible representation matrices. As they are the same for every symmetry operation in the same class, it is only necessary to list classes, not in general every individual operation.

From the above, we have Character Table below for C2v:

C2v	E	C2	σv	σ’v
A1	1	1	1	1	z,z2,x2,y2
A2	1	1	-1	-1	Rz,xy
B1	1	-1	1	-1	x,zx,Rx
B2	1	-1	-1	1	y,zy,Ry

• Along the top are the classes of operations listed.
• Along the left are the labels of the irreducible representations.
• The data shows the traces of the representation matrices.
• The right hand column lists the functions forming a basis for each representation.

The number and the dimensions of the irreducible representations of a group are governed by two rules:

1. The number of irreducible representations is the same as the number of symmetry classes.
2. The sum of the squares of the dimensions of the irreducible representations is the order of the group (i.e. the total number of symmetry operations).

Thus, C2v has 4 classes so the order is 4. There must be 4 irreducible representations, all one-dimensional.

Labelling of Irreducible Representations:

1. One dimensional representations are labelled A or B, according to their behaviour (+1 or -1) under rotation about the principal axis.
2. Two and Three Dimensional representations are labelled E and T respectively. Occasionally F is used instead of T in older books on vib spec.
3. When there is an inversion centre, representations are given subscripts g and u (gerade – even, and u – odd), according to their behaviour under inversion.
4. When there is a horizontal reflection plane but no inversion, representations are given primes ‘ or double primes “ according to their behaviour under reflection in this plane.

Every point group has an irreducible representation called “totally symmetric”, for which all characters are +1.

The Reduction Formula

Reduces the representation spanned by a set of basis functions.

Where:

• n(i) = Number of times the ith irreducible representation occurs in the representation r that we are aiming to reduce.
• h = Order of the group, i.e. the number of operations in the group (not always the same as number of classes!)
• χr(R) = character of the reducible representation r under the symmetry operation R.
• χi(R) = character of the irreducible representation I under the symmetry operation R.

Consider for example the problem of finding the irreducible representations spanned by the set of 4H 1s basis functions in the methane molecule. Each operation is represented by a (4x4) matrix, but we are only interested in the diagonal sum of the transformation matrix.

Remembering that it is only when an atom is unshifted that it can contribute to this sum it is easily seen that the characters χr(R) are given simply by the number of H atoms that are unshifted under each symmetry operation. Moreover, it is always the case that the character is the same for each symmetry operation of a given class so we need inspect the effects of only one operation within each class.

Td	E	8C3	3C2	6S4	6σd
A1	1	1	1	1	1	x2+y2+z2
A2	1	1	1	-1	-1
E	2	-1	2	0	0	(2z2-x2-y2, x2-y2)
T1	3	0	-1	1	-1	(Rx, Ry, Rz)
T2	3	0	-1	-1	1	(x,y,z) (xy, xz, yz)
Γ(H1s)	4	1	0	0	2

n(A1)         =         (1/24)(4x1x1 + 1x1x8 + 0x1x3 + 0x1x6 + 2x1x6)                 =         1

n(A2)         =         (1/24)(4x1x1 + 1x1x8 + 0x1x3 + 0x1x6 + 2x-1x6)         =         0

n(E)         =         (1/24)(4x2x1 + 1x-1x8 + 0x2x3 + 0x0x6 + 2x0x6)         =         0

n(T1)         =         (1/24)(4x3x1 + 1x0x8 + 0x-1x3 + 0x1x6 + 2x-1x6)         =         0

n(T2)         =         (1/24)(4x3x1 + 1x0x8 + 0x1x3 + 0x1x6 + 2x1x6)                 =         1

Γ(1Hs) =         A1 + T2

Some notes about application of the reduction formula

• in evaluating the summation given in the equation we deal with each class of symmetry operation in turn. We multiply the character for Γ(1Hs) (appearing underneath the character table on the previous page) by the character for the relevant irreducible representation and then multiply by the numbers of operations in a given class. Thus each term is a product of three numbers, and will be zero if any of the three is zero.
• We can check that we have obtained the correct answer by verifying that the characters for the irreducible representations we have derived add up to the set of characters for the representation we are trying to reduce.
• The n(i) must always be zero or integral. If they are not something has gone wrong somewhere!
• The number of symmetry adapted functions must always be the same as the number of basis functions. In the present case we start with 4 basis functions and end up with A1 + T2 irreducible representations. The latter is 3-fold degenerate so there are 4 symmetry adapted combinations.

Matrices and Representations in Higher Order Point Groups

More complicated for C4 compared to C2 because values of X and Y are inextricably scrambled by this operation.

General Expression for the character of Cn1:

Rotation in a plane generates the matrix:

This has the character:

χCn = 2 cos θ + 1

The character of the matrix for the Cn1 operation will be identical to the character of the matrix for Cn-1 (i.e. Cnn-1).

Note that the matrices for C31 and C32 (as an example) will be different, even though the characters are the same. These particular matrices are:

Matrices for the reflection operations:

In the plane of an axis:

This is reflection so that Y→-Y.

For planes at an angle φ to the x-axis, the general matrix is:

The trace of thee are always = 1, however.

All these operations together form a set of 2x2 matrices linked to X and Y, and a 1x1 matrix of Z. The 2x2 matrix is an example of the scrambling of X and Y together, as for the C41 operation earlier.

Now, the characters can be used to describe the operations as follows:

C3v	E	C31	C32	σ1	σ2	σ3
ΓXYZ	3	0	0	1	1	1

This reduces to: A1 + E.

We know from the above matrices that ΓZ = A1 and ΓXY = E. This also explains where the (x,y) for E and z for A1 come from in the character table.

Tables of Descent in Symmetry

These tables summarise results of the sort we have been discussing. They show how functions corresponding to a given irreducible representation in a group of high symmetry behave in sub-groups of lower symmetry.

R3 (the group of a sphere)	O	D4	D3
S	A1	A1	A1
P	T1	A2 + E	A2 + E
D	E + T2	A1 + B1 + B2 + E	A1 + 2E
F	A2 + T1 + T2	A1 + B1 + B2 + 2E	A1 + 2A2 + 2E
G	A2 + E + T1 + T2	2A1 + A2 + B1 + B2 + 2E	2A1 + 2A2 + 3E
H	E + 2T1 + T2	A1 + 2A2 + B1 + B2 + 3E	A1 + 2A2 + 4E

Jahn-Teller Theorem

A system with an orbitally degenerate ground state must distort so as to relieve the degeneracy.

Tables of descent in symmetry are useful in decided which sort of distortion will lift the symmetry as required by this theorem. Consider for example an octahedral system.

Squashing or elongation along one of the C4 axes takes us into the D4h point group.

Squashing or elongation along one of the C3 axes takes up into the D3d point group.

If we have a d1 configuration with one electron in a t2g orbital we have a T2g state. The degeneracy of such a state is lifted by either distortion. By contrast in a d9 state with a t2g6eg3 configuration and an Eg ground state only the distortion to D4h will lift the degeneracy.

2nd Order Jahn-Teller Effects

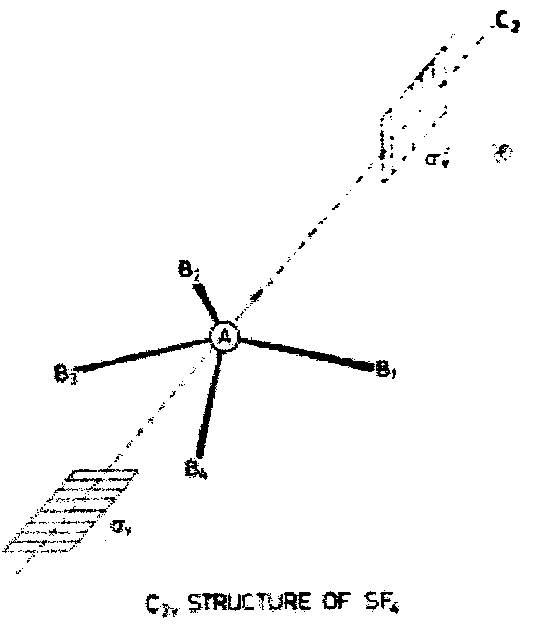
Group theoretical arguments provide an alternative approach to the VSEPR model for rationalising the structures of simple polyatomic molecules. Consider for example the σ-bonding in SF4. An MO diagram constructed in a hypothetical tetrahedral geometry has occupied bonding t2 and a1 levels as in CF4, but in addition the antibonding a1 level must be also occupied by two electrons. The empty t2 antibonding level lies at higher energy and is unoccupied. Consider now a distortion to a lower symmetry.

Descent of symmetry tables tells us that the a1 wavefunction must remain totally symmetric. The threefold degeneracy of the t2 level will be lifted. Provided that one component of t2 is also totally symmetric, the occupied antibonding (the HOMO) can mix with one of the t2 components (the LUMO). This will stabilise the lower electronic level.

On this basis distortions to C2v or C3v symmetry would lower the electronic energy, but distortion to D2d or D4h would not. The former two structure are exactly those introduced in simple VSEPR arguments.

Molecular Vibrations

Linear molecules have 3N-5 vibrational degrees of freedom, while non-linear molecules have 3N-6. These correspond to 3 translational degrees of freedom and either 2 or 3 rotational degrees of freedom.

In order to determine the symmetries of the various translations, vibrations and rotations, it is necessary to determine the irreducible representations of using x, y and z coordinates for all the atoms present.

Deriving Γmol:

Considering the shifting of atoms. Contributions to the character from unshifted atoms can be generalised.

Character as a result of a Cn operation:

χCn = 2 cos θ + 1

Thus for C2, θ = 180o so cos(180o) = -1 and the character is -1.

Character as a result of a Sn operation:

χSn = 2 cos θ - 1 (due to reversal along z)

Thus, can derive anything, since E = C1, i = S2 and σ = S1.

General Procedure for determining symmetries of molecular vibrations

Use the relationship:

Γvib = Γmol – Γtrans - Γrot

Γtrans and Γrot can be identified from the character table by those elements with Rx,y,z for rotation and x,y,z for translation.

Thus all the steps are:

1. Identify the positions of the symmetry elements and establish the molecular point group.
2. Work out the characters of the matrices which make up Γmol. This is achieved using the unshifted atom approach, taking account of the contributions made to the character by those symmetry operations which leave atoms unshifted.
3. Use the Reduction Formula to obtain the irreducible representations present in Γmol.
4. Use the character table to identify the irreducible representations for translation and rotation, and subtract these representations from Γmol.

From here we now have an representation Γvib for all the vibrations. However, these can be further be distinguished by stretches (along bonds) and bends (everything else).

Consider now the unshifted bond approach. Analyse each operation in turn and see how many bonds of the molecule are unshifted, and then reduce this. This gives Γstretch.

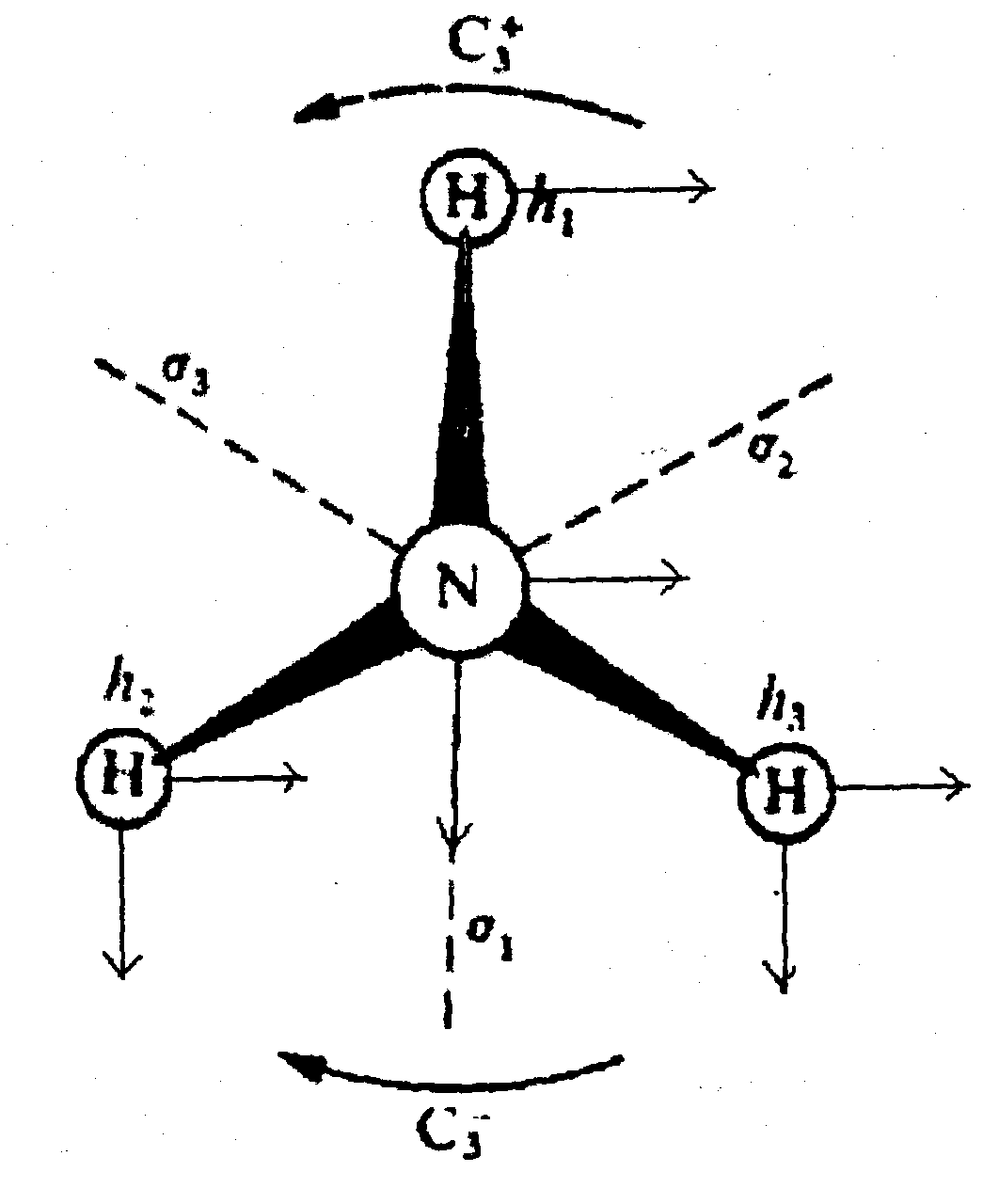
For example, in H2O:

E	C2	σv	σv’
2	0	2	0

This reduces to A1 + B1.

For H2O Γvib = 2A1+B1, therefore Γbend must be A1.

Note that each vibrational mode in a molecule has a unique frequency. Thus for H2O there are two at 3756 cm-1 and 3657 cm-1 and a third at 1595cm-1. The latter corresponds to the bend. It is also usually found that the number of stretching modes is equal to the number of bonds.

Also of note, it is always possible to stretch a set of equivalent bonds such that the full symmetry of the molecule is preserved. What this means is that for a set of equivalent bonds there will always be a totally symmetric representation.

Vibrational Spectroscopy

IR Spectroscopy –

Absorption of EM radiation at a vibrational transition energy. Only those vibrations with particular symmetries can absorb it.

Symmetry Selection Rule for IR Spectroscopy:

A vibration will be active in the infrared if it has the same symmetry as one of the functions x,y or z.

What this corresponds to is a change in dipole moment of the molecule.

Raman Spectroscopy –

Emission of light in which the energies associated with vibrational transitions appear as shifts in frequency from a higher energy exciting line.

Symmetry Selection Rule for Raman Spectroscopy:

A vibration will be active in the Raman if it belongs to the same representations as one of the functions x2, y2, z2, xz, yz, or xy.

This corresponds to a change in the polarisability of the molecule.

These functions may appear as linear combinations (e.g. x2-y2) when considering a point group with degenerate representations.

Mutual Exclusion

In centrosymmetric molecules, any vibration which is active in the IR will be inactive in the Raman, and vice versa. This comes about because in a centrosymmetric molecule, x,y,z are always u-type representations, whilst squared and crossed terms are always the g-type.

This can be useful for distinguishing cis and trans isomers, or tetrahedral and square planar configurations.

Molecular Vibrations

In general the vibration of a polyatomic molecule does not involve deformation of an individual bond or bond angle.

Instead molecular vibration involves excitation of normal modes of vibration of a molecule. A normal mode of vibration involves a synchronous deformation of the molecule in which the displacement vectors describing the motion of individual atoms combine so as to belong to one of the irreducible representations of the molecule. The atoms all undergo their displacements at the same frequency and all pass through the equilibrium configuration at the same time.

Basis Sets for Molecular Vibrations

A set of 3N displacement vectors with 3 vectors attached to each of the N atoms in a polyatomic molecule will form the basis for construction of 3N symmetry adapted functions. However, 3 of these must correspond to translation of the molecule as a whole in three orthogonal directions. In non-linear molecules a further 3 correspond to molecular rotation about three mutually perpendicular axes. For non-linear molecules there are only 2 rotational degree of freedom. Thus we find 3N-6 modes of normal modes of vibration for non-linear molecules and 3N-5 for linear molecules. In high symmetry molecules some of the modes may be grouped together in degenerate sets.

For polyatomic molecules of the sort ABn or ABnCm with a unique central atom (e.g. XeF4, XeO3F2 but not B2Cl4) it may often be advantageous to work with a basis set of 3N-3 vectors, omitting the 3 vectors on the central atom: these will always correspond simply to the translation of the molecule, so that with this basis set we generate vibrations plus rotations.

Finally in many situations, a problem will focus only on stretching vibrations. In particular we often want to know about stretching vibrations in ABn polyatomics or about carbonyl stretches or cyanide stretching vibrations in complexes. In these cases we can use a much simpler basis set which consists simply of a set of n vectors along the bond directions. This basis set will generate the n stretching vibrations without any redundancy.

Using Bond Stretching Basis Sets

In general we need to write down the characters of the transformation matrices which describe the effects of each symmetry operation in the group on the chosen basis set. Vectors on a given atom only contribute to the diagonal sum if the atom is unshifted. When we are dealing with the set of n bond stretching vectors in an ABn molecule this gives us the simple rule:

Character under operation R = χ(R) = number of B atoms unshifted under the operation.

We can now apply these ideas to deduce the irreducible representations for bond stretching vectors in SF4, CF4 and XeF4.

SF4 (Point Group C2v)

C2v	E	C2	σv	σ’v
A1	1	1	1	1	z	z2, x2, y2
A2	1	1	-1	-1	Rz	xy
B1	1	-1	1	-1	x, Rx	zx
B2	1	-1	-1	1	y, Ry	Zy
Γstretch	4	0	2	2

Applying the Reduction Formula:

n(A1) = ¼ (4+0+2+2)         = 2

n(A2) = ¼ (4+0-2-2)         = 0

n(B1) = ¼ (4+0+2-2)         = 1

n(B2) = ¼ (4+0-2+2)         = 1

Hence Γstretch = 2A1 + B1 + B2

All 4 modes are both IR and Raman active. We can derive the same result by recognising that there are two different sorts of F atom. For each pair an in phase combination of stretches gives an A1 mode, whilst the out of phase combinations generate the B1 and B2 modes. This simple consideration allows us to sketch out the displacement vectors in the stretching modes.

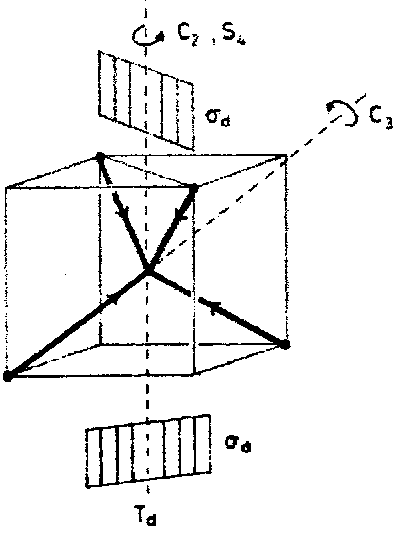
CF4 (Point Group Td)

Td	E	8C3	3C2	6S4	6σd
A1	1	1	1	1	1	x2+y2+z2
A2	1	1	1	-1	-1
E	2	-1	2	0	0	(2z2-x2-y2, x2-y2)
T1	3	0	-1	1	-1	(Rx,Ry,Rz)
T2	3	0	-1	-1	1	(x,y,z) (zy,xz,yz)
Γ(H 1s)	4	1	0	0	2

The character table is provided, and the Γ representation is found by the unshifted atoms approach.

From this, the Reduction Formula can be applied as:

n(A1) = 1/24 (4x1x1 + 1x1x8 + 0x1x3 + 0x1x6 + 2x1x6)                 = 1

n(A2) = 1/24 (4x1x1 + 1x1x8 + 0x1x3 + 0x1x6 + 2x-1x6)                 = 0

n(E) = 1/24 (4x2x1 + 1x1x8 + 0 + 0 + 0)                                 = 0

n(T1) = 1/24 (4x3x1 + 0 + 0 + 0 + 2x-1x6)                        = 0

n(T2) = 1/24 (4x3x1 + 0 + 0 + 0 + 2x1x6)                         = 1

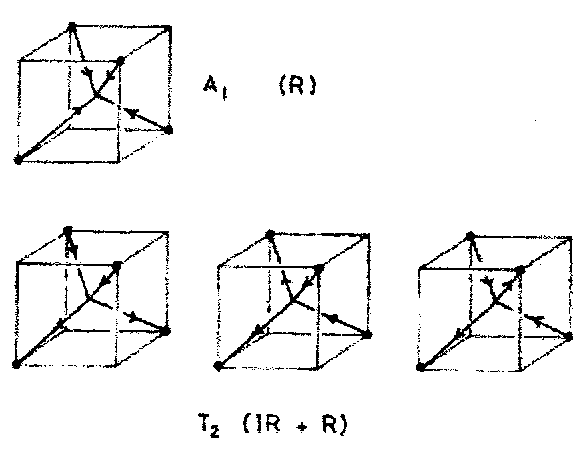
It is thus found that Γ(H 1s) reduces to A1 + T2.

Notes:

n(i) is ALWAYS an integer or zero.

The value can be checked by applying the character table values for the reduced representation (A1+T2) and checking that it gives the irreducible representation (bottom row of the table above).

The number of functions obtained always matches the number of basis functions. Thus, we started with 4 basis functions (4 H’s) and have obtained A1+T2 (1 + 3 representations).

A1 is only Raman active; T2 is both IR and Raman active. The form of the A1 mode is trivially obvious. We can sketch the form of the T2 modes by noting that they are of the same symmetry as p orbitals on the central atom. We use a convention that the displacement vector points towards a + sign on the orbital and away from a – sign.

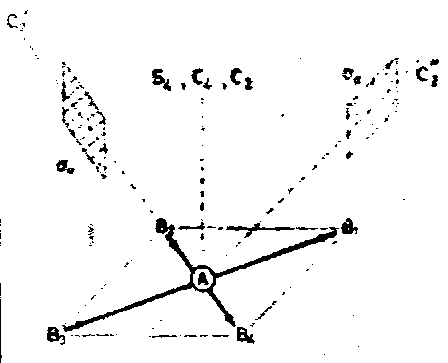
XeF4 (Point Group D4h)

Application of the reduction formula is tedious in this case but we can simplify the calculation somewhat by recognising that the in-plane stretch vector can not possible generate any irreducible representations that change sign under the σh operation. Hence we ignore Eg and the ungerade A and B representations.

This means Γstretch reduces to A1g + B1g + Eu.

Of these modes, A1g and B1g are Raman active and Eu is IR active. A mutual exclusion rule applies, as in all centrosymmetric systems. Because the dipole moment operator is u and the components of the polarisability tensor are g, no mode can be both Raman and IR active in a molecule with a centre of symmetry.

A Full Vibrational Analysis (not just stretches) can also be carried out, although it is more lengthy. The same result is reached:

Draw up a table:

	E	2C4	C2	2C2’	2C2’’	i	2S4	σh	2σv	2σd
# unshifted atoms	5	1	1	3	1	1	1	5	3	1
Contribution per atom	3	1	-1	-1	-1	-3	-1	1	1	1
Γmol	15	1	-1	-3	-1	-3	-1	5	3	1

From this, the Reduction Formula gives:

Γmol = A1g + A2g + 2A2u + B2g + B1g + B2u + Eg + 3Eu

Subtracting Γtrans and Γrot gives:

Γvib = A1g + A2u + B1g + B2g + B2u + 2Eu

Analyse stretching modes by the unshifted bonds approach:

	E	2C4	C2	2C2’	2C2’’	i	2S4	σh	2σv	2σd
Γstretch	4	0	0	2	0	0	0	4	2	0

This reduces to A1g + B1g + Eu, as above.

A1g is the totally symmetric stretch (all 4 bonds outwards).

B1g is also centrosymmetric, with two opposite bonds stretching while the other two bonds at 90o compressing.

Eu is doubly degenerate, and there is no centre of symmetry (u-type). They take the form of two mutually perpendicular vibrations taking place along the x and y axes. They correspond to one distinct absorption as a whole.

The bending modes can be obtained from Γvib - Γstretch, which gives A2u + B2g + B2u + Eu.

Mutual exclusion of IR and Raman spectra due to the centrosymmetric nature of the molecule implies that the IR corresponds to A2u and Eu, while the Raman active are A1g, B1g and B2g.

Vibrations in NH3

NH3 belongs to the point group C3v and we can tackle the problem of deriving the symmetry of its normal modes of vibration using a “complete” basis set with 3 vectors on each of the 4 atoms.

The major new problem encountered with this basis set is the effect of the 3-fold rotation on the vectors (x,y,z) on the N atom. In general if we use R(α) to indicate rotation by an angle α:

Thus the character for a trio of vectors (x,y,z) under rotation by α is 1+2 cos α.

For C3+, α = 120o so that cos α = -½ and the trace of the transformation matrix for C3+ is χ(120o) = 0. Similarly for C3- α = 240o and again cos α = - ½ and χ(240)o = 0. This illustrates the general point that the character is always the same for two operation of the same class. Thus when dealing with reflections we can choose for convenience that σ1 mirror plane where two vectors on H1 and the N atom are unshifted under σ and one changes sign so that the contribution from each atom to χ(σ) is +1. Thus we derive the set of characters shown below:

C3v	E	2C3	3σv
A1	1	1	1	z	x2+y2, z2
A2	1	1	-1	Rz
E	-2	-1	0	(x,y) (Rx,Ry)	(x2-y2, xy) (xz, yz)
Unshifted atoms	3	1	2
χ(3N)	12	0	2

Application of the reduction formula gives:

Γ3N = 3A1 + A2 + 4E

Γtrans = A1 + E

Γrot = A2 + E

Γvib = 2A1 + 2E

using a set of 3 stretching vectors it can be quickly shown that:

Γstretch = A1 + E

So that:

Γbend = A1 + E

Where stretching and bending modes are of the same symmetry, mixing between them is allowed.

The Vibrations of C60

Group Theory played an important part in its discovery by making the simple prediction that the molecule should have only 4 infrared active vibrations.

C60 is a rare example of a molecule belonging to the icosahedral point group Ih. the 3N-6 rule tells us that there are no less than 174 modes of vibration and on the face of it the problem of deriving the symmetry of these modes is formidable. The character table also looks very unfriendly! The group order h=120 and there are 10 irreducible representations including 4-fold degenerate G representations and 5-fold H representations not encountered in other molecular point groups.

Nonetheless it turns out to be very easy to derive the normal modes of vibration. This is because none of the rotational symmetry axes passes through an atomic position and the character of the basis set of 180 displacement vectors under the rotational operations is zero. The character under inversion i is also zero. The 15 mirrow planes each contains 4 atoms so that character under σ is (4x2-4x1) = 4. The only other operation where a non-zero character appears is under the identity operation, where χ(E) = 180. Application of the reduction formula is therefore much less problematic than expected. It transpires that there are only 4 IR active T1u modes and 8 Raman active Hg modes.