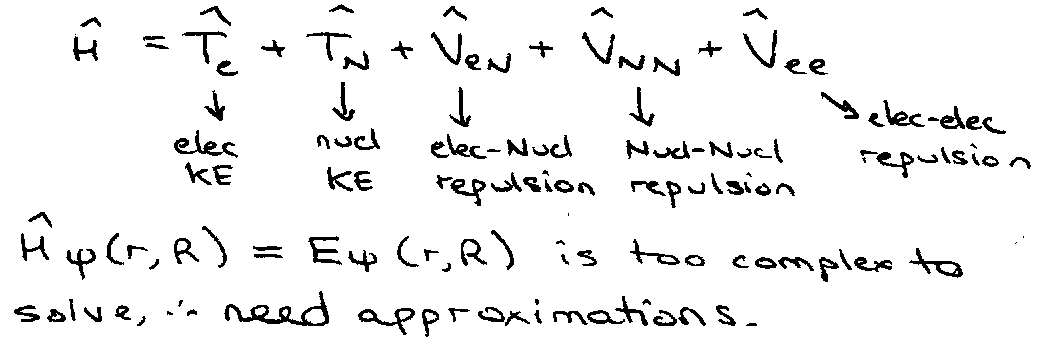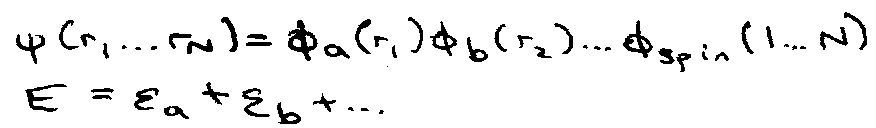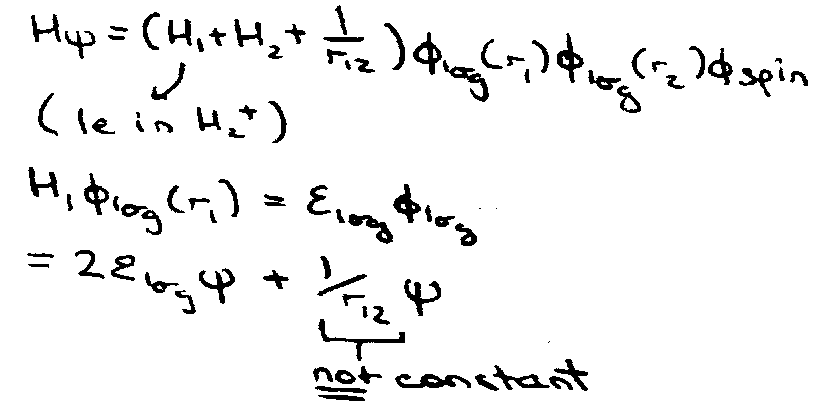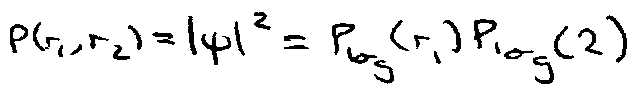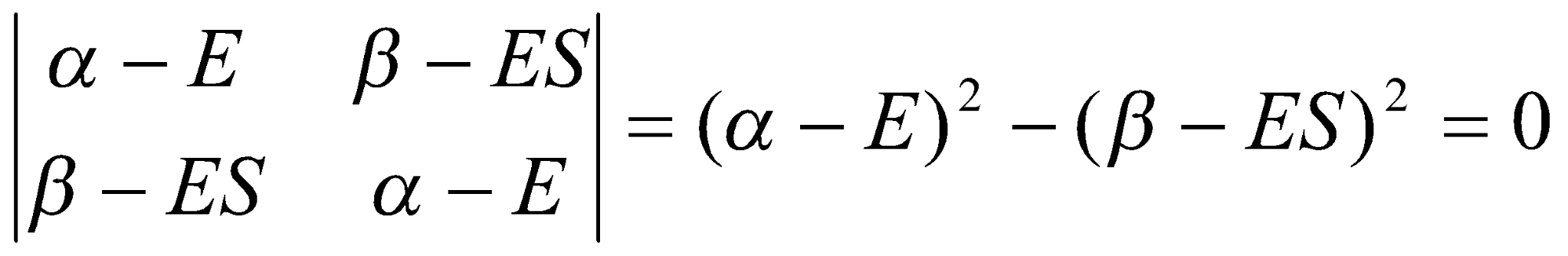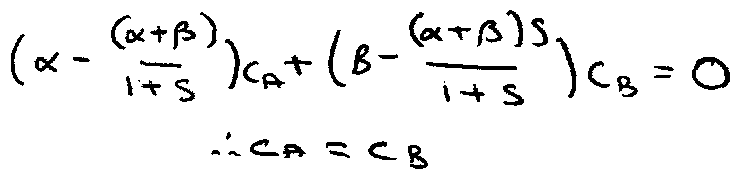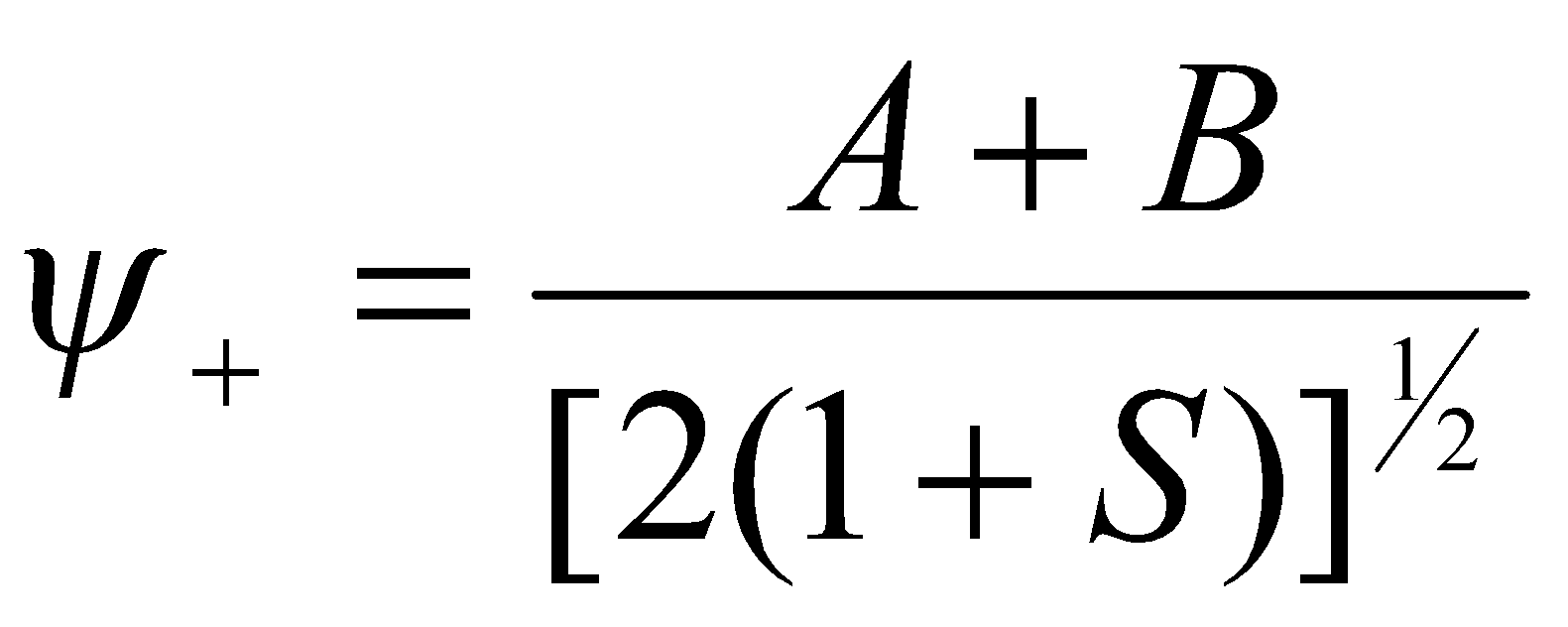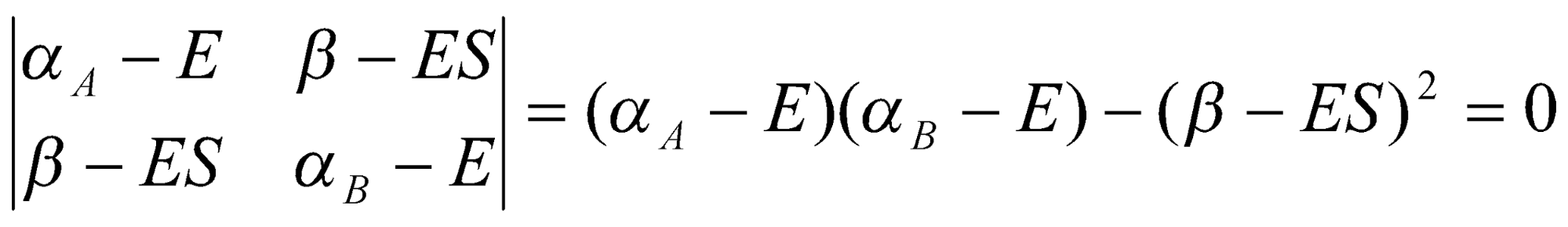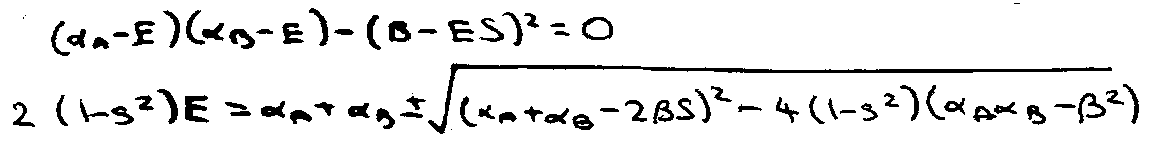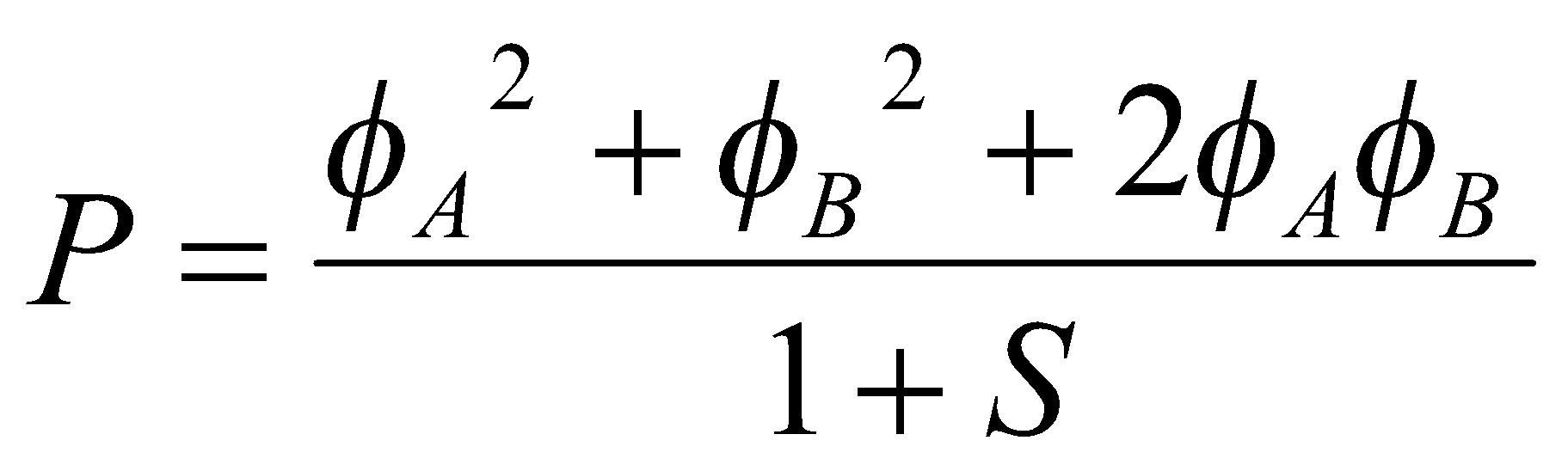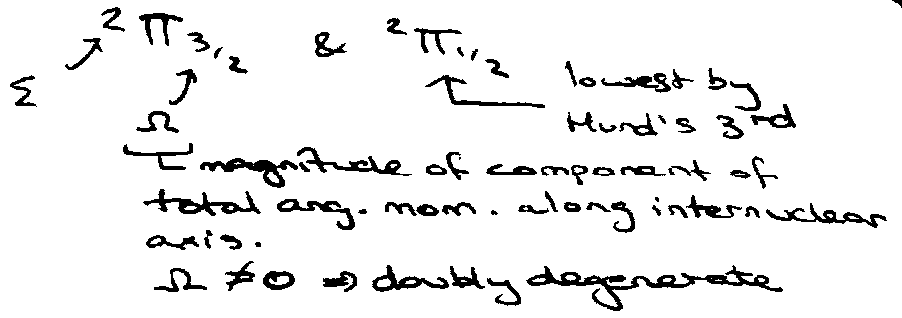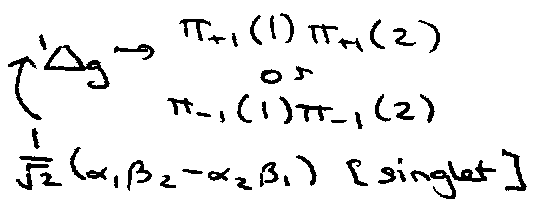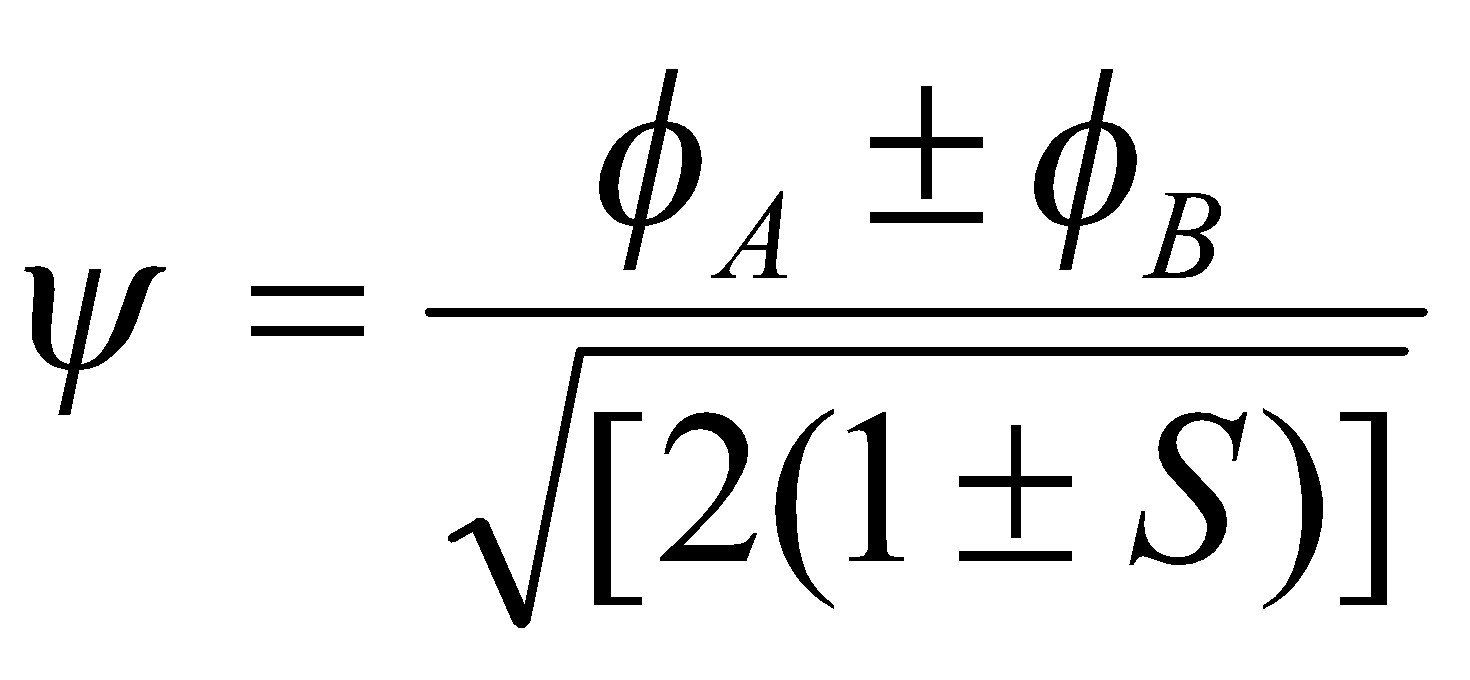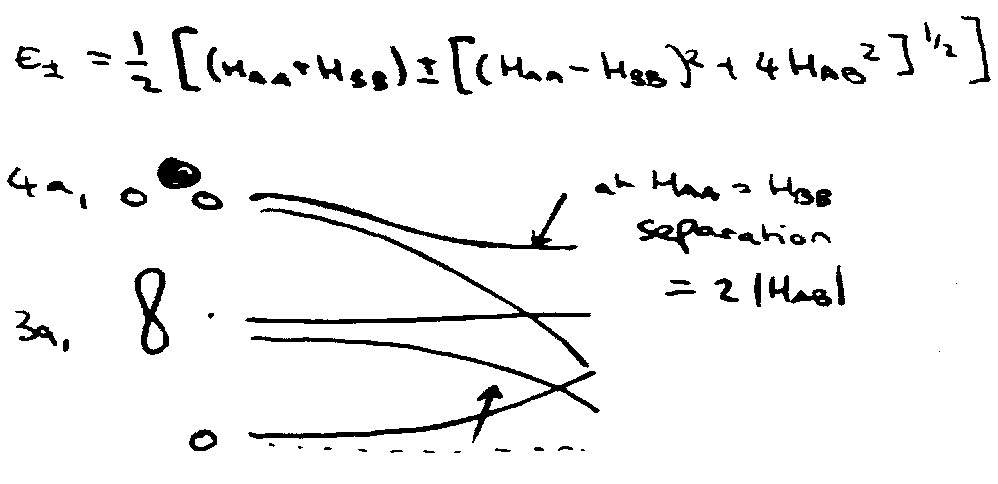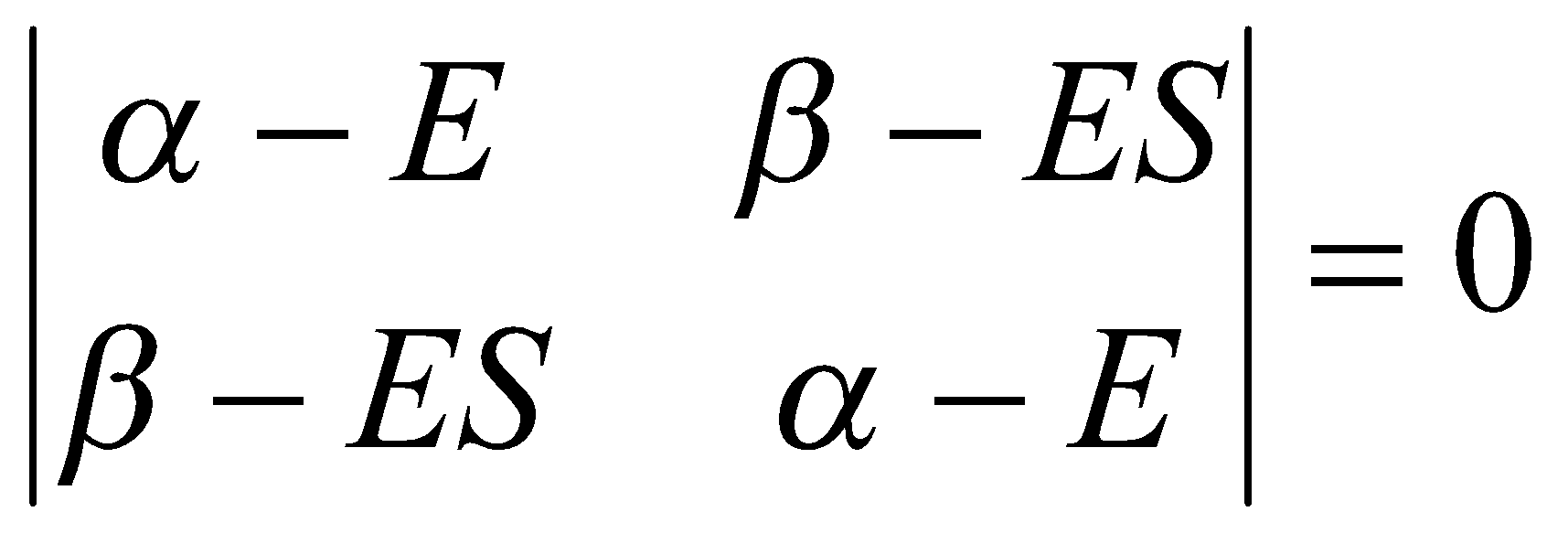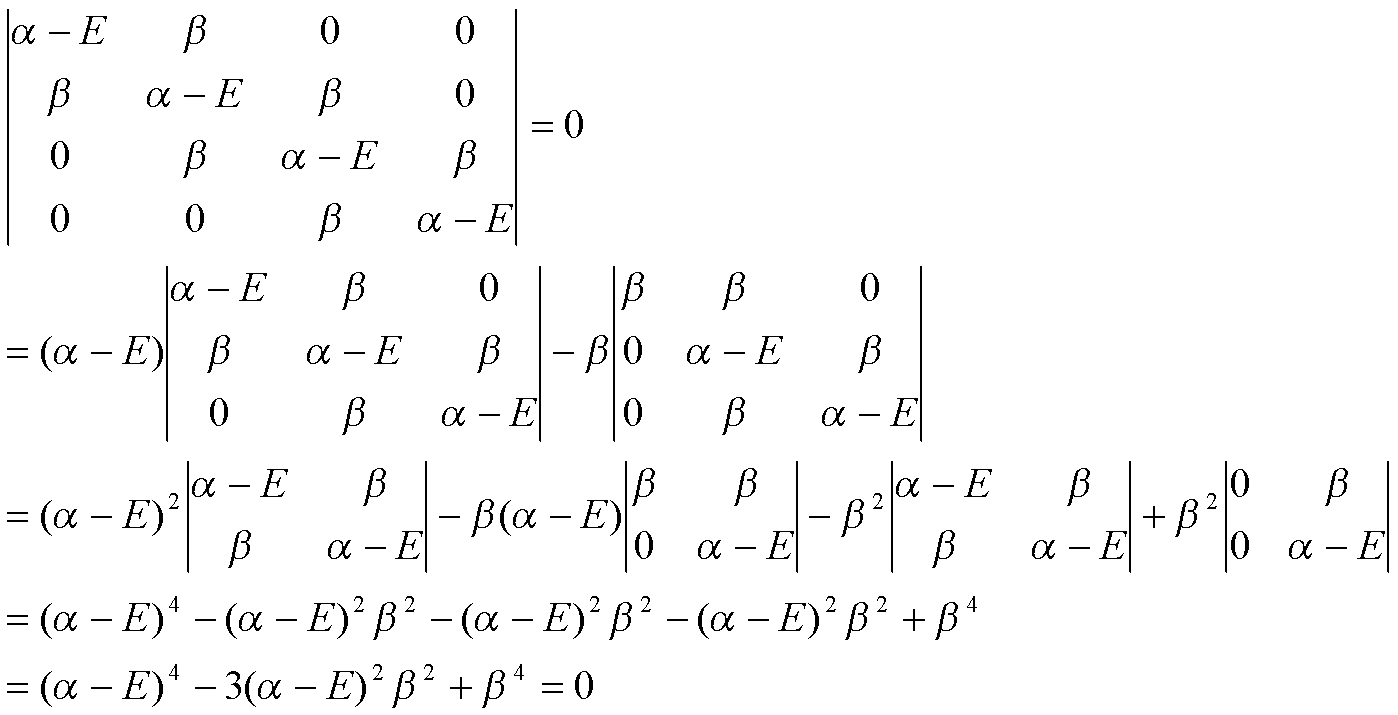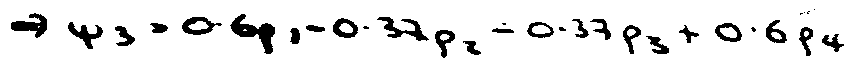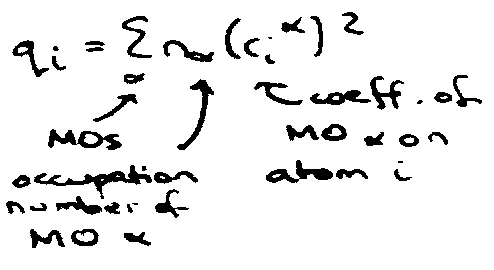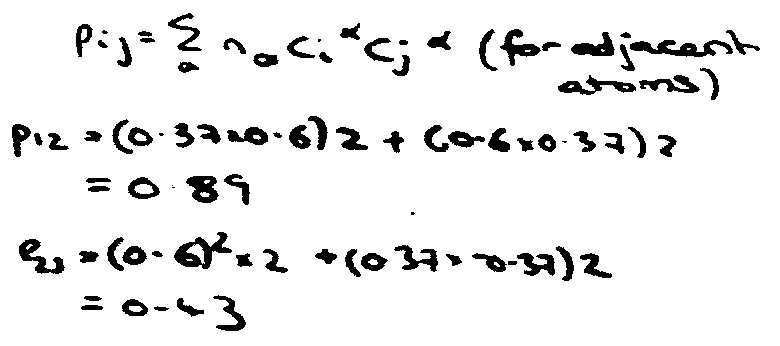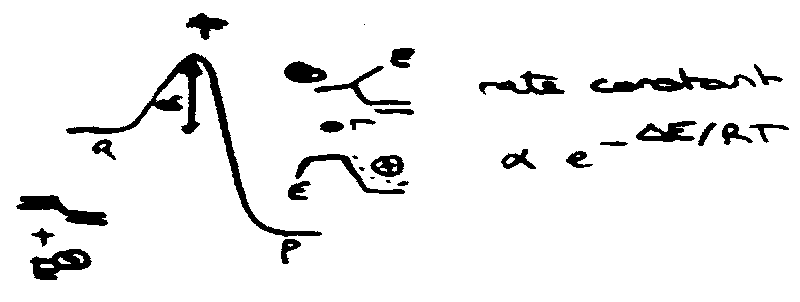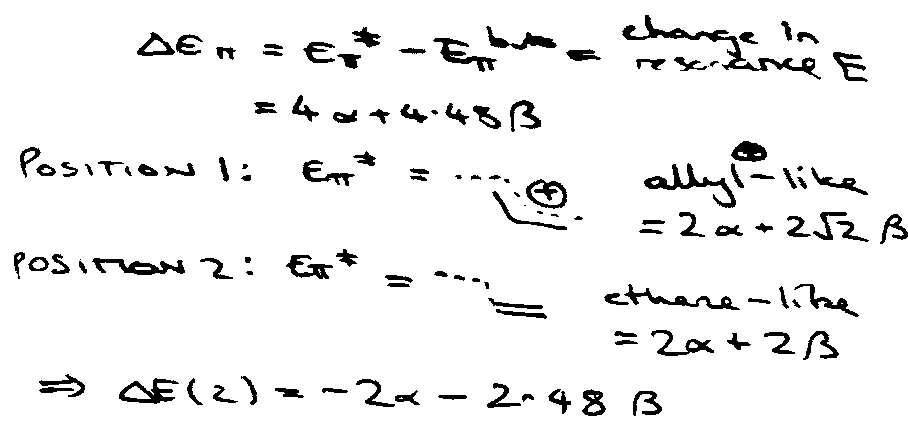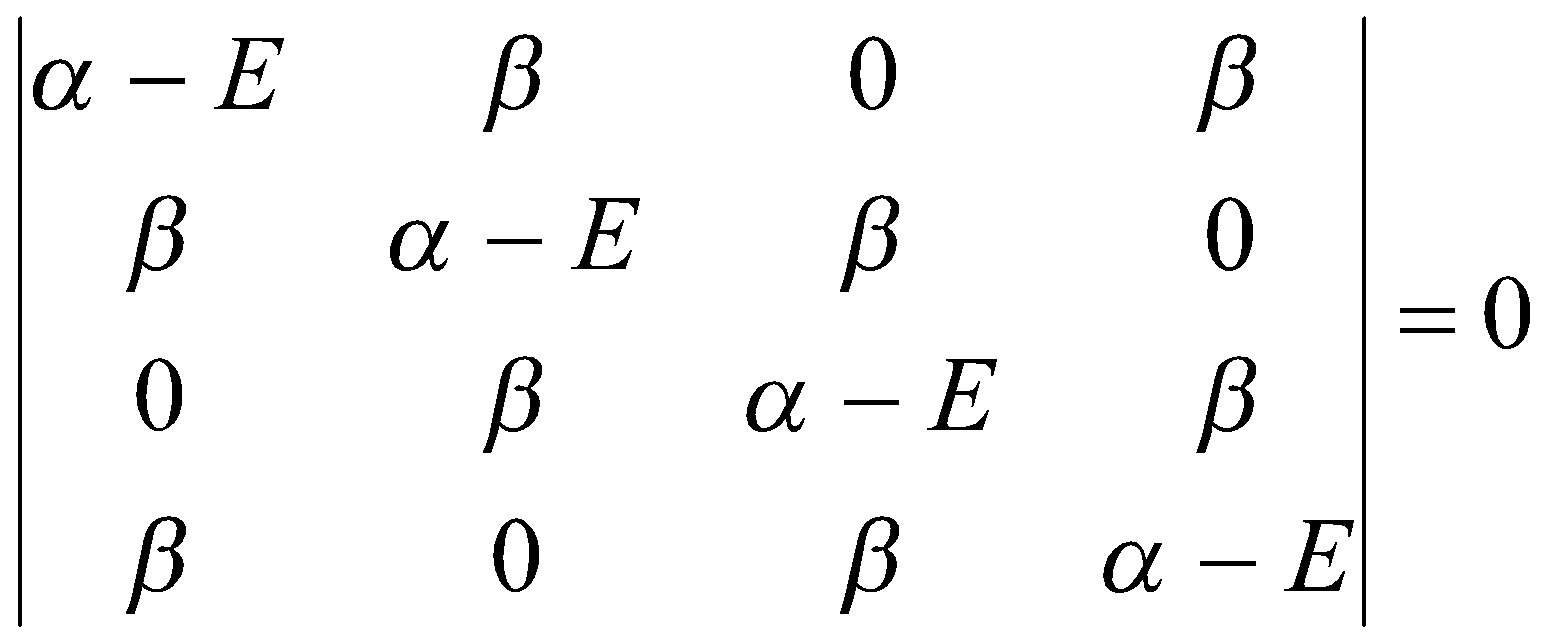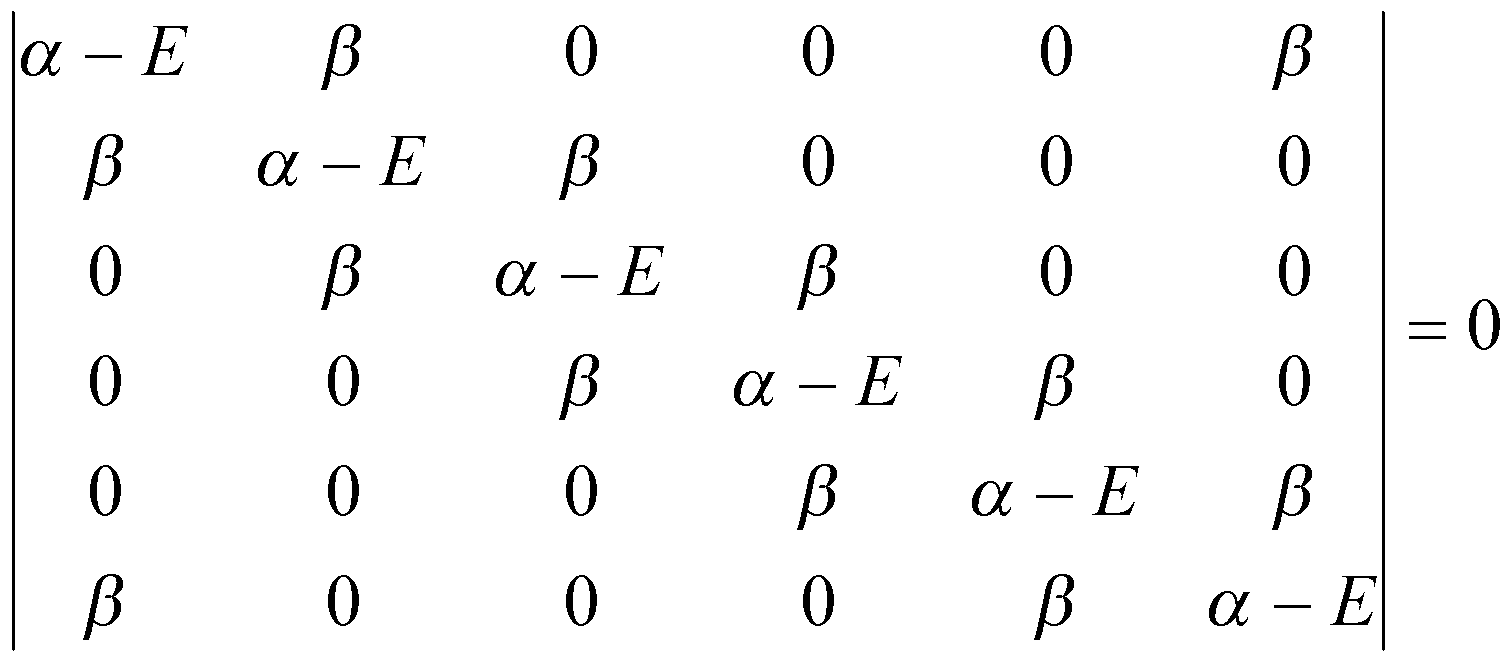Valence & Electronic Spectroscopy Notes

Born-Oppenheimer Approximation

For a molecular system, Hamiltonian:

H2+ -

Define He = H – TN         [ Electronic Hamiltonian ]

For stationary nuclei, suppose we’ve solved the electronic problem:

B-O Approx:

Assume ψ(r|R) is a slowly varying function of nuclear positions.

When not applicable –

1. 2 states have same energy.
2. “curve crossing” – fast nuclear motion, e.g. in ionic system.

Molecular Orbitals & the LCAO Approach

MO Theory starts by supposing that the main ideas of the self-consistent-field method for atoms may be applied equally well to molecules, based on the following fundamental principle – each electron in a molecule is described by a certain wavefunction ψ, where the electron is spread over the whole molecule as opposed to being centred on any particular atom(s). Otherwise it can be treated like an atomic orbital in terms of electron-density, quantum numbers, etc.

The most obvious characteristic for an MO of a diatomic molecule is that it is bicentric. It is this which distinguishes it from an AO. The most appropriate physical description is that the electron moves in an orbital which encloses the neighbourhood of both nuclei.

When the electron is in the region of one of the nuclei, the forces on it are those due chiefly to that nucleus and to the other electrons near that nucleus. Disregarding the electron interactions, the wavefunction will be similar to that for H2+. We notice that when the electron is near nucleus A, the most significant parts of the Hamiltonian are precisely those terms which would comprise the Hamiltonian of an electron in the field of A alone. This means that in the neighbourhood of nucleus A, the MO resembles an AO φA. Since the complete MO has characteristics separately possessed by φA and φB, it is a natural step to adopt the method of a linear combination:

Solving the Electronic Problem for H2+

Symmetry constraints on e-density, ρ(r):

Equal at all points related by symmetry, therefore cA = ± cB ≡ c.

Normalisation:

Therefore 2 possible wavefunctions:

With densities:

= sum of atomic densities.

φAφB is large where orbitals overlap.

ψo – extra density between nuclei (reduces elsewhere by (1+SAB)

ψ1 – reduces density between nuclei and increases it elsewhere.

Evaluation of energy,

HAA = HBB; HAB = HBA (identical 1s orbitals).

Resulting Energy expressions have (J+K) = bonding, (J-K) = antibonding.

The integrals –

NOTES:

Exponential.

J(R) cancels 1/R.

k(R) dominant and antibonding orbitals more antibonding than bonding is bonding.

LCAO – solves H2+ exactly, but really only a guide – non-quantitative.

Some Terminology

Down symmetry axis:

g,u → parity (behaviour under inversion). g = even, u = odd.

Orbital Approximation

For Many Electron Molecules

• total wavefunction associated with a “configuration”.
• Construct according to exclusion principle.

Orbitals –

1 electron wavefunction used in construction of many electron wavefunction.

Nature of Orbital Approximation –

H2 ground state:

Labelling –

Doubly occupied orbital → totally symmetric representation.

For O2, Π x Π from electronic configuration:

Predictions of Orbital Approximation –

Molecule	Configuration	Term Symbol	# Bonding e’s	R
H2+	1σg1	2Σg+	1	1.06
H2	1σg2	1Σg+	2	0.74
He2+	1σg21σu1	2Σu+	1	1.08
He2	1σg11σu2	1Σg+	0	-

→ Qualitative correspondence with observation.

Does it satisfy Hψ = Eψ:

No dependence on spin in H →

Therefore ψ must depend explicitly on r12, i.e. wavefunction must be correlated (e1 knows where e2 is).

IMPROVEMENTS:

• allow orbitals to vary so as to minimise average inter-electron repulsion (by Variation Principle).
• Self-consistent field or Hartree-Fock orbitals (later).

But does NOT eliminate neglect of correlation.

Consequences of Orbital Approximation

1. He2 predicted to be unbound (antibonding more antibonding than bonding is bonding). In reality, electron positions are correlated → van der Waals (dispersion) attraction.

In orbital approximation:

= product of probabilities → electron positions intrinsically independent.

2. Incorrect description of dissociation. Examine large R behaviour of e-density in MO for H2.

Cross terms vanish as R → ∞, i.e. dissociation products = 2H• + H++H- → De’s very bad.

The Variation Principle

Simple way of finding coefficients in the LCAO approach to build Molecular Orbitals. Vary the coefficients of a trial wavefunction until the lowest energy is achieved (by evaluating the expectation value of the Hamiltonian for each wavefunction).

Hence let ψ contain some variable parameters and minimise energy wrt them.

For a two orbital problem (A and B), must find the coefficients for which:

, and

First step is to express the two integral in terms of the coefficients.

The denominator is:

This equals cA2+cB2+2cAcBS, because the individual AOs are normalised and the third integral is the overlap integral, S.

The numerator is:

These integrals are often expressed as shown. Hence:

The completed expression for E is thus:

Its minimum is found by differentiation with respect to the two coefficients and setting the result equal to 0. The result is:

(αA - E)cA + (β - ES)cB = 0

(β - ES)cA + (αB - E)cB = 0

These are the two secular equations.

The parameter α is called a Coulomb integral. It is the energy of the electron when it occupies A or B respectively, and is negative. In a homonuclear diatomic, αA = αB = α.

The parameter β is called a resonance integral. It vanishes when the orbitals do not overlap, and at equilibrium bond lengths it is normally negative.

To solve the secular equations for the coefficients we need to know the energy E of the orbital. As for any set of simultaneous equations, the secular equations have a solution if the secular determinant is zero, that is, if:

This expands to a quadratic equation in E. Its two roots give the energies of the bonding and antibonding MOs as follows:

Let this be a homonuclear diatomic (αA = αB = α).

The solutions to this equation are:

The values of the linear combination are obtained by solving the secular equations using the two energies obtained from the secular determinant. The lower energy gives the coefficients for the bonding MO, the upper energy the coefficients for the antibonding MO.

The secular equations gives expressions for the ratio of the coefficients in each case, so we need a further equation in order to find their individual values. This equation is obtained by demanding that the best wavefunction should also be normalised. This conditions means that, at this final stage, we must ensure that:

Examples

Homonuclear Diatomic

Have shown above that

The solutions are thus (subbing back into Secular Equations):

And similarly for the other solution:

In this case, the bonding orbital has the form:

And the corresponding antibonding orbital:

Heteronuclear Diatomic

Common procedure to simplify is to set S = 0 (usually a good guide).

The solutions can be expressed in terms of the parameter ξ:

And are:

E- = αA - β cot ξ                ψ− = −A sin ξ + B cos ξ

E+ = αA + β cot ξ         ψ+ = A cos ξ + B sin ξ

An important feature revealed by these solutions is that as the difference |αA - αB| increases, the value of ξ decreases. When the energy difference is large the energies of the MOs differ only slightly from those of the AOs, which implies in turn that the bonding and antibonding effects are small. That is, the strongest bonding and antibonding effects are obtained when the two contributing orbitals have closely similar energies. The difference in energy between core and valence orbitals is the justification for neglecting the contribution of core orbitals to bonding. The core orbitals of one atom have a similar energy to the core orbitals of the other atom; but core-core interaction is largely negligible because the overlap integral between them (and hence the value of β) is so small.

If | αA - αB | = 2 | β |:

If β/|αA-αB| is small → binomial expansion.

Covalency maximised when αA - αB = 0.

Wavefunctions:

General Observations

Orbitals of different symmetry do not mix, since Hij = φi H φj = β and Sij = φi φj vanish.

Orbitals of very different energies do not mix, since β/(Hii-Hij) is small.

Non-crossing rule – energies of 2 states of same symmetry can never be equal (as β ≠ 0).

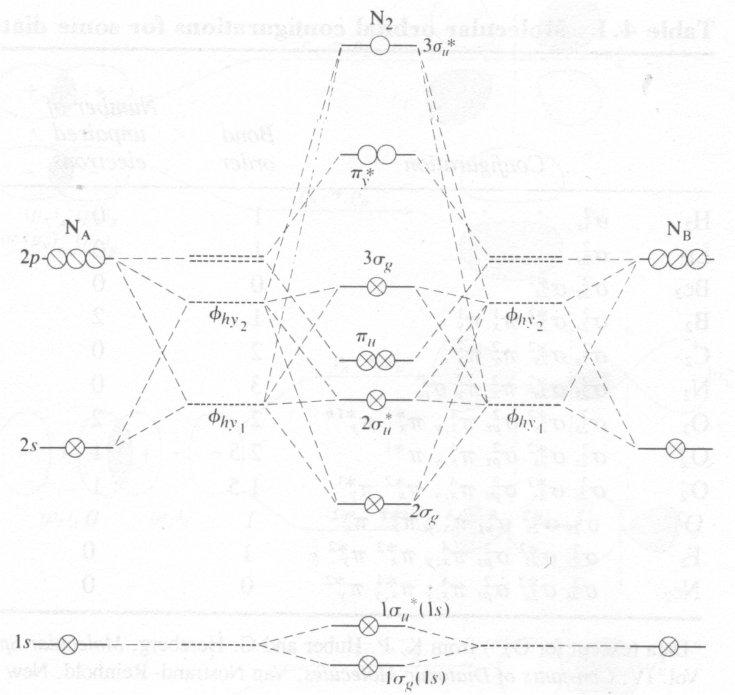
1st Row Homonuclear Diatomics

Expect MO’s of 1s,2s,2px …

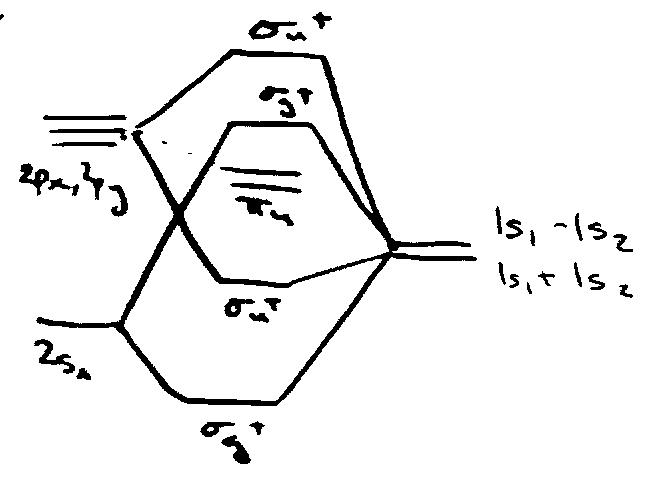
The Hydrogen Molecule

This follows on easily from the H2+ case, with an extra electron in the ground state orbital formed for that. Considering the electron density of the MO by evaluating P = 2ψ2, we find that:

P = 2N+2(φA2 + φB2 + 2φAφB)

The normalising factor may be evaluated as usual, which gives N+2 = 1/2(1+S). Hence,

Integrating over all space we obtain the total charge, namely two electrons, but the contributions to P come from three regions: the first (φA2) term is the electron density in a single H atom (A) multiplied by 1/(1+S), so the corresponding charge contribution is 1/(1+S) as φA2 is normalised. Similarly, the second terms gives the same contribution from the B atom. The final term gives a contribution 2S/(1+S) arising from the overlap region where φA and φB both have substantial values. This gives us a graphic way of describing the bond.

Other Homonuclear Diatomics

We can extend the ideas above in general for 1st row diatomics quite easily. When two identical atoms are brought together, the AOs φA and φB are replaced by MOs of the form N±(φA±φB). One of these will be bonding and the other antibonding, and the difference in energy between the two being determined by the appropriate bond integral β. At large distances the energies of both MOs tend to the energy of the AOs. This gives rise to the pictorial representations and terminology earlier.

Rule 1 – 2 AO’s only make large contribution to an MO if Atomic Energies are similar.

Rule 2 – orbitals on different atoms with zero overlap do not contribute to the same MO.

Hence, ignore mixing of 1s with 2s,2p. 2s mixes with 2p.

Heavy and Light Atoms

If 2s and 2p interaction negligible, E2p – E2s >> bonding interaction → limit of large “penetration” = heavy atoms (O2 upwards). No mixing.

Heavy:

But lighter → mixing.

→ “light” atoms (H2 → N2).

Different spatial arrangements of electrons → different inter-electron repulsion Energies.

Order of energies is 3Σg- < 1Δg < 1Σg+

(cf. Hund’s Rules).

Splitting of Ground State Configuration

(NO, O2+).

O2+ & NO: [Be2] 3σg21πu41πg1 → 2Π.

Split due to Spin-Orbit Coupling (diagram right) –

Different energies due to magnetic interaction ~ 0.02eV.

Hence,

MΩ = MΣ + MΛ.

Splitting of Ground State in O2 and C2 (excited) is due to inter-electron repulsion.

O2 = [Be2] 3σg21πu41πg2 → 2 1Πg, which from direct product tables gives: 3Σg- + 1Δg + 1Σg+

2 orbitals are associated with the 2 orientations of the components of the orbital angular momentum (λ) along the internuclear axis:

Heteronuclear Diatomic Molecules

The same principles that apply to homonuclear diatomics can be extended to here, except for the fact that the coefficients cA and cB are no longer necessarily equal. Thus, contrasting the homonuclear and heteronuclear cases:

Homonuclear, αA = αB

We have already shown that in this case, αA = αB = α, and hence:

, and

The correlation between the bonding and antibonding levels and those in unbonded atoms is shown.

When S << 1, the splitting of the AO levels is 2β, and since the magnitude of β (assumed negative) is larger the larger the overlap, we obtain a basis for the principle of maximum overlap. The forms of ψ1 and ψ2 are independent of β, being determined by symmetry, and in each MO the two AOs occur with equal weight at all internuclear distances.

Heteronuclear, αA ≠ αB

Instead of solving the quadratic equation directly, we may obtain the general character of the result by a simple approximation. The effect of interaction arises from the term (β-ES)2, whose neglect leads to the solutions E = αA or E = αB, corresponding to the uncombined AOs. Let us suppose that αA is the lower of the two AO energies (i.e. atom A is more electronegative than atom B) and suppose the bonding MO has an energy close to αA. We can then substitute E ≈ αA everywhere except in the factor αA – E to estimate how much E is changed by the interaction. This yields:

(αA-E)(αB-αΑ) − (β−αAS)2 = 0

 Which gives, on rearranging, the bonding MO energy:

The lower of the AO energies is thus pushed down by approximately β2/(αB-αA) (for S = 0) to give the energy of the bonding MO. A similar argument shows that the upper level is pushed up by the same amount (for S = 0), i.e.

This can be summarised pictorially:

In a heteronuclear molecule, a bonding MO leans towards the more electronegative atom (A in our case), while its antibonding partner leans towards the less electronegative atom (B).

Shape of AH2 Molecules

For 1st row A, valence MOs involve 2sA, 2pxA, 2pyA, 2pzA and 2 x 1s on H.

In linear (D∞h) geometry:

2sA                 →                 σg+                [ 1s1 + 1s2 = σg+ ]

2pzA                 →                 σu+                [ 1s1 – 1s2 = σu+ ]

2pxA, 2pyA         →                 πu

Expect:

But now consider change as molecule bends: D∞h → C2v (descent in symmetry).

Walsh Diagram:

Non-crossing Rule

Consider mixing of 3a1 and 4a1:

”mixing” of orbitals -         ψ =         cAφA + cBφB

                                     3a1      4a1

Secular Equations:

Curves can only cross if A and B are of different symmetry at crossing point, (HAA = HBB), since HAB will then vanish.

Huckel Theory

In this approach, the π orbitals are treated separately from the σ orbitals, which is useful for conjugated molecules (i.e. those with a σ-framework with double bonds alternating). All the carbon atoms are treated identically, so all the Coulomb integrals α for the atomic orbitals that contribute to the π orbitals are set equal.

The Secular Determinant

LCAO approach for C 2p orbitals that lie perpendicular to the molecular plane. In ethene we would write ψ = cAA + cBB, and in butadiene ψ = cAA + cBB + cCC + cDD.

For π electron systems of organic molecules.

The optimum coefficients and energies are found by the variation principle as above. That is, we have to solve the secular determinant. Examples:

Ethene –

Butadiene –

The roots of ethene determinant can be found easily, but we can see that the butadiene in one is far more complex. The following addition Huckel Approximations are useful:

1. All overlap integrals are set equal to zero.
2. All resonance integrals between non-neighbours are set to zero.
3. All remaining resonance integrals are set equal (to β).

More concisely:

• Hii = < pi | H | pi > = α (same for all atoms).
• Hij = < pi | H | pj > = β (i bonded to j – negative).
• Sij = δij ( = 1 if i = j, =0 otherwise).

These approximations are obviously very severe, but they let us calculate at least a general picture of the molecular orbital energy levels with very little work. There are no distinctions between cis, trans, linear in Huckel Theory. The assumptions result in the following structure for the secular determinant:

1. All diagonal elements are α - E
2. Off-diagonal elements between neighbouring atoms are β.
3. All other elements are 0.

Ethene

Allyl

Secular Determinant is:

Need to find the roots to this. Clearly Eo = α is a root. Also, (α-E)2 = 2β2 → E± = α ± β√2

Thus, 3 roots, as expected from a 3x3 determinant:

Eo = α

E+ = α + β√2

E- = α - β√2

For Eo, can see from the determinant that a = -c, therefore ψo = (1/√2)(φA-φB)

For E±, (α-E)a + βb = 0, hence a = ±(b/√2), so ψ± = (φA/2) ± (φB/√2) + (φC/2)

Physically,

Butadiene

With x = (α-E)2/β2, the expanded determinant has the form of a quadratic equation x2 – 3x + 1 = 0. The roots are x = 2.62 and 0.38. Therefore, the energies of the four LCAO-MOs are:

E = α±1.62β, α±0.62β.

2-fold symmetry, therefore symmetry-adapted AOs:

MO corresponding to E1(ψ1) – sub into Secular Equations.

-1.62βc1 + βc2 = 0, therefore

c1 = c2/1.62

Similarly MO for ψ3 –

The lower 2x2 → E2 = α + 0.62β; E4 = α - 1.62β.

Gives:

This can be shown as:

An important point emerges when we calculate the total π-electron binding energy, Eπ, the sum of the energies of each π-electron, and compare it with what we find in ethene. In ethene the total energy is:

Eπ = 2(α+β) = 2α+2β.

In butadiene it is:

Eπ = 2(α+1.62β) + 2(α+0.62β) = 4α+4.48β.

Therefore the energy of the butadiene molecule lies lower by 0.48β (about -36 kJ mol-1) than the sum of two individual π-bonds. This extra stabilisation of a conjugated system is the delocalisation energy, or resonance stabilisation energy.

Charge Density on Atoms

Equal charge on all atoms is a general property of alternant hydrocarbons.

Bond Order

i.e. only partial π-bond between central atoms.

Bond length in excited state:

p12 = 2x(0.37x0.6) + (0.6x0.37) + (0.6x-0.37) = 0.45

p23 = 2x(0.6)2 + (-0.37x0.37) + (-0.37)2 = 0.72

Expect expansion of outer bond, contraction of central on excitation → vibrational excitation in electronic spectrum (Franck-Condon).

Electron Paramagnetic Resonance

Signal for Radical Cation.

Hyperfine Coupling to protons is proportional to unpaired e-density on adjacent carbon.

Susceptibility to Electrophilic Attack

ΔE = ΔEσ + ΔEπ

i.e. change in energy of σ/π electrons. Imagine that ΔEσ insensitive to position of attack.

Hence, attack at position 1 is preferred.

Rings & Aromaticity

Estimating the delocalisation energy in these requires first finding the energies of the π-orbitals by Huckel Theory.

For example, with cyclobutadiene, the secular determinant is set up using the same basis as for butadiene, but note that atoms A and D are also now neighbours. Then solve for the roots of the secular equation and assess the total π-bond energy. For the delocalisation energy, subtract from the total π-bond energy of two π-bonds.

Secular Determinant:

(Note that the top right and bottom left corners are now β instead of 0).

This determinant expands t:

x(x-4) = 0, x = [(α-E)/β]2

The solutions are x = 0 and x = 4, so the energies of the orbitals are:

E = α+2β, α, α, α-2β

Four electrons must be accommodated. Two occupy the lowest orbital (energy α+2β) and two occupy the doubly degenerate orbitals (energy α). The total energy is therefore 4α+4β. Two isolated π-bonds would have the same energy, therefore cyclobutadiene has no stabilising delocalisation energy.

Benzene, on the other hand, is known to be stabilised. The Huckel Approximation as above gives rise to the following Secular Determinant:

The roots of this are:

E = α±2β, α±β, α±β

These have symmetry labels associated with them (a2u, e1g, e2u, b2g). It is noted that the lowest energy orbital is bonding between all neighbouring atoms, the highest energy orbital is antibonding between each pair of neighbours, and the intermediate orbitals are a mixture of bonding, non-bonding and antibonding character between adjacent atoms.

We find that the π-electron energy of benzene is:

Eπ = 2(α+2β) + 4(α+β) = 6α + 8β.

The delocalisation energy is thus 2β (~150 kJ mol-1).

Cyclic Polyenes –

E = α + 2β cos iπ/k

For Even Membered Rings:

N = 4:

N = 6:

N = 8:

For Odd Membered Rings, modify as N = 2k-1.

E = α + 2β cos [2πi/(2k-1)]

Results give rise to Huckel’s 4n+2 Rule. The rule refers to the properties of cyclic conjugated molecules in which there are N π-electrons; these depend on the nature of the integer N. If N is expressed in terms of a smaller integer n the rule may be stated as follows:

• N = 4n+2 → the molecule is highly stable.
• N = 4n+1 → the molecule is a free radical.
• N = 4n → the molecule has a triplet ground state and is highly unstable.

The reason for this is clear from the following diagram, which shows the distribution of energy levels about the reference level E = α for conjugated rings with N atoms:

Because there is a single lowest orbital, while the others occur in degenerate pairs, the number of filled or partly filled levels must be of the form 1+2n (with n degenerate pairs); they will be exactly filled, to give a closed-shell ground state, by twice this number of electrons, i.e. N = 4n+2. If N is reduced by one the highest degenerate pair will contain only three electrons, the single occupied MO giving radical behaviour. If N is reduced by 2 the remaining two electrons will occupy the degenerate MO’s singly with spins parallel (Hund’s Rules), giving a triplet state.

The 4n+2 rule is illustrated by benzene, cyclopentadienyl, and cyclobutadiene. Benzene is highly stabilised (N=4n+2 with n=1), cyclopentadienyl has radical properties (N=4n+1 with n=1), while cyclobutadiene (N=4n with n=1) should be highly unstable. Note that the cyclopentadienyl anion is stabilised (N=4n+2 with n=2), as is the cyclpropenium cation (N=4n+2 with n=0).