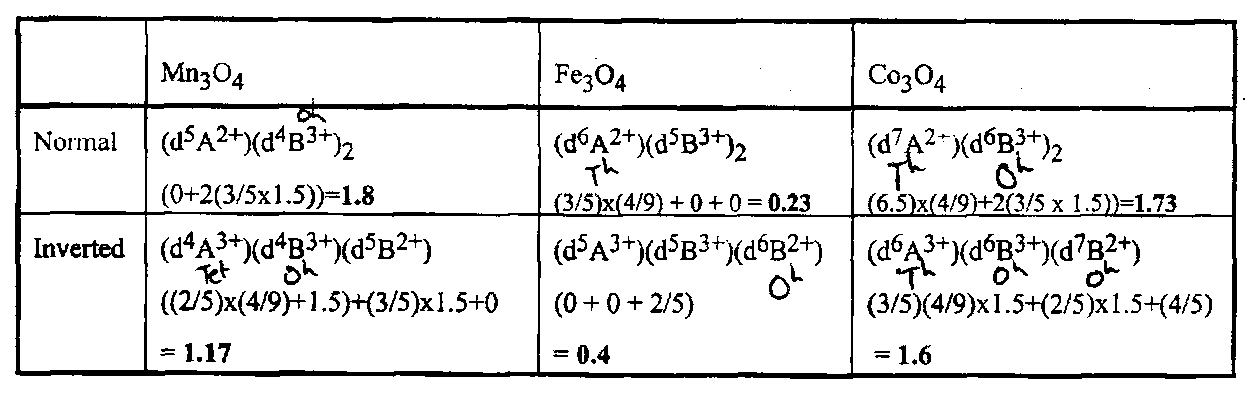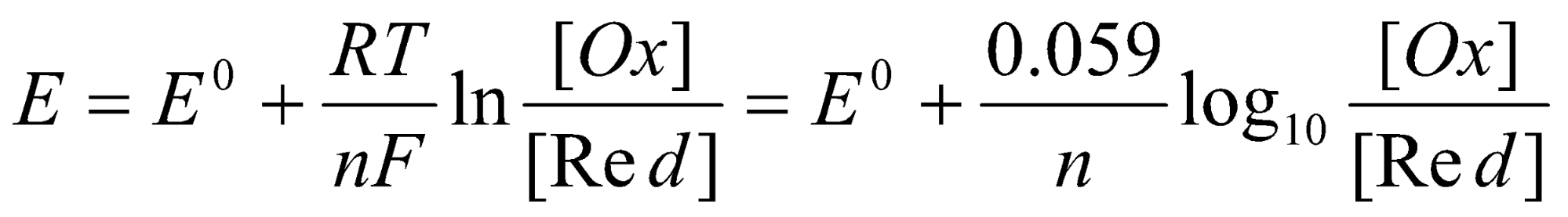Transition Metals Notes

Characteristics of Transition Metals

They are typically electropositive, and always have a partially filled d-subshell. This often leads to paramagnetism. They form coloured complexes in solution and have a variable set of oxidation states (often conferring catalytic activity). Sc and Zn do not exhibit transition metal chemistry because their d-subshell is empty / full respectively, and all this chemistry is brought about by this being partially filled.

Energies and Trends

Atomic Configurations

Atomic spectrum of neutral atom gives ground state electron configuration. The results are scattered for the transition metals.

Ionisation always results in the loss of an s electron. Relative energies of 4s and 3d change drastically with the charge on the atom.

Obtain the effective nuclear charge, Zeff, from the orbital energy: εorb = -Iorb = -Zeff2RH/norb2. The trend shows the rapid stabilisation of 3d vs. 4s

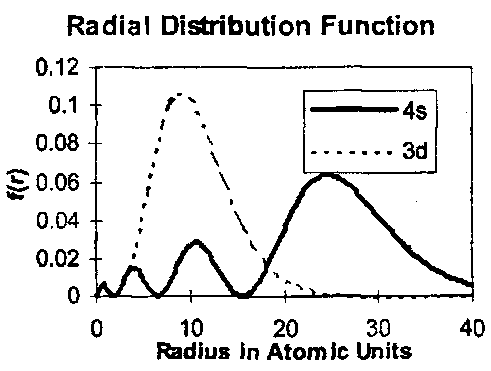
The changeover is due to the different penetration properties of the two types of orbital. The probability that an electron is at a distance r is given by the Radial Distribution Function. Its potential energy is proportional to 1/r but must be weighted by this probability. These functions are plotted for the H atom.

Although the innermost lobe of 4s is very small, it is significant for the energy, whose value is obtained by integrating from r=0 to infinity, because of the 1/r dependence. In the H atom the integrals for 3d and 4s are in the ratio 16:9 as expected, and 3d is much more stable than 4s. In heavier atoms, the presence of the inner lobe of 4s allows relatively unscreened access to the full nuclear charge, compared to 3d, and at potassium 4s is more stable than 3d.

Trends in Orbital Energies

In a sequence of transition metal atoms, both nuclear charge and 3d electrons are added. The 4s orbital energy is subject to two competing influences:

1. The small and penetrating innermost lobe of 4s experiences a steady increase in nuclear charge, about 1 in 25 for each element.
2. The large outermost lobe of 4s is effectively screened from this increase by the interposition of 3d electron density of smaller average radius.

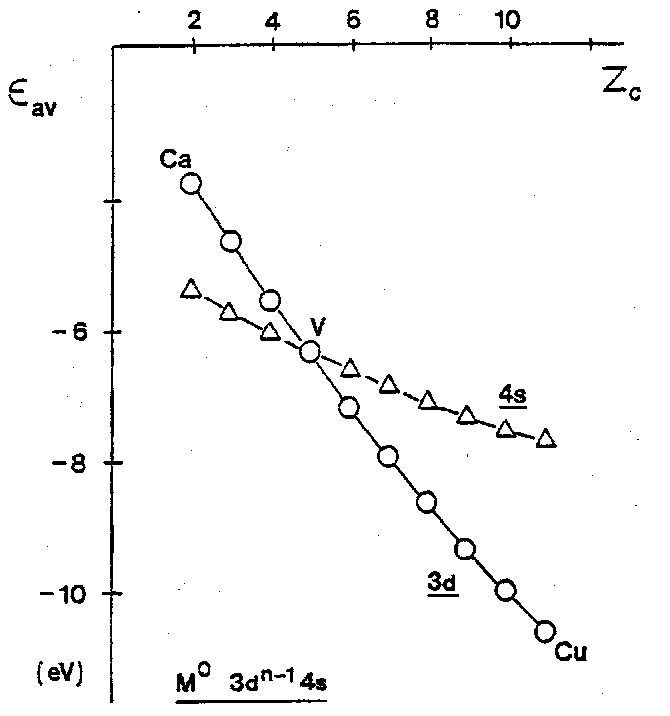
The result is a rather slow increase in the stability of the 4s orbital across the series of neutral transition metal atoms. By contrast, the 3d electrons, being all of the same average radius, are not effective at screening one another from the increase in nuclear charge, and their energy therefore drops more sharply than the 4s. This can be seen in the average of configuration orbital energies for the 3dn-14s configurations.

Effect of Ionisation

The ionisation of valence electrons does not much change the screening of the nuclear charge in the inner regions of penetrating orbitals (e.g. 4s), but has a larger influence on Zeff in non-penetrating orbitals, by reducing their screening. So ionisation stabilises the non-penetrating 3d orbitals relative to the penetrating 4s orbitals. In the limit, the removal of enough screening electrons must return the relative orbital energies to the H atom sequence, with 3d << 4s.

The vital point is that in all TM ions, all the valence electrons are d electrons. We can ignore the s shell. Even in compounds in low oxidation states, the larger average radius of the 4s orbital ensures that it overlaps well with orbitals on other atoms, and becomes part of a strongly antibonding molecular orbital which is unoccupied. For all practical purposes the occupied valence shell is well described in terms of d orbitals alone.

The relative 3d-4s orbital energies shown do not explain the neutral atom ground state configurations. One might expect all atoms after Vanadium to have only 3d electrons. Instead we find either 3dn-24s2 or 3dn-14s1. This happens because the electrons in the ground state arrange themselves to minimise electron-electron repulsion, which is proportional to 1/r12. the distance r12 between electrons depends on the diffuseness of the orbitals, and is on average larger in 4s than 3d. Ground states therefore gain stability in configurations containing s electrons. Exceptions occur with d5 and d10 configurations, which for special reasons (see later) have unusually low mutual repulsion between d electrons.

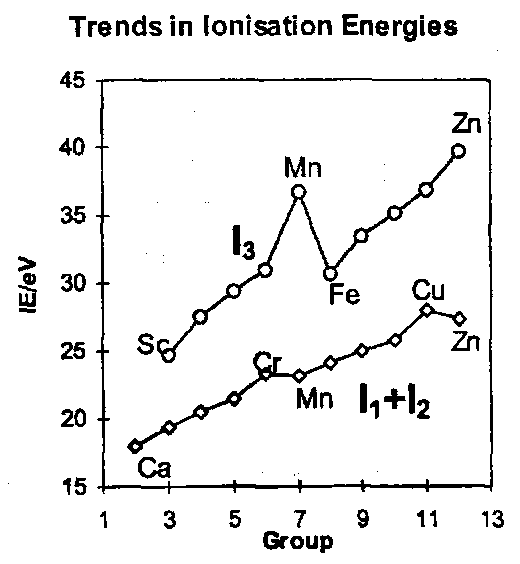
To summarise, the important TM valence orbitals are d orbitals, and their energy becomes lower, both with increasing positive charge on the ion (oxidation state) and with the increasing Zeff across a TM series of elements. The effect is obvious in the ionisation energies. It is this trend that dominates the chemistry of these elements, drastically reducing the electropositivity of the elements as their atomic number increases.

Notice the high values of I1+I2 at Cr and Cu. Both are due to exceptionally large values of I2, which involves the ionisation of a d electron from d5 and d10 ions respectively. Notice this happens again for I3 with Mn, which corresponds to ionisation from d5 as well.

The Role of Electron Spin

Quantum mechanics predicts that the repulsion between electrons depends not only on the distance between electrons but on their relative spin. The antisymmetrisation of the electronic wavefunction with respect to the interchange of a pair of electrons means that the probability that two electrons of parallel spin are located at the same point in space must be zero, but this is not true of electrons of opposed spin. This means that the mean Coulomb repulsion energy is smaller for a pair of electrons of parallel spin because on average they are further apart than a pair of opposed spin. The energy difference is called the Spin-Correlation Energy or alternatively the Exchange Energy, and is the origin of Hund’s First Rule. The electron-electron repulsion energy is a composite of a Coulomb contribution for a pair of electrons plus an Exchange contribution (always negative) for each pair with parallel spins. Exchange Energy is thus a stabilising influence.

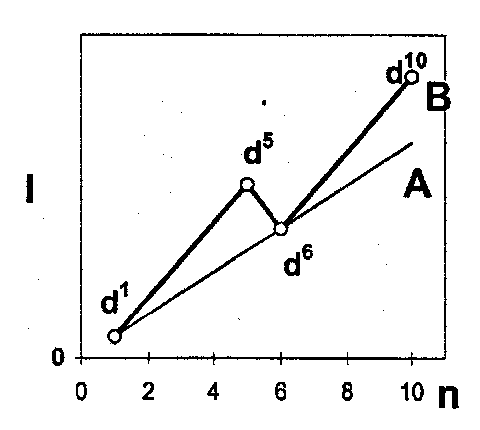
The maximum loss of stabilisation is found at n=5 and n=10, which correlates with the ionisation energies. A plot of ionisation energy against n has a pattern shown on the right.

The line A is just the linear variation of the change in the core and Coulomb energy, and line B shows the effect of adding the Exchange Energy. This ends up resembling the 3rd ionisation energy plot above.

This trend has major implications for the stability of the III oxidation state compared to the II. The easiest way to see this is to list the stable trihalides, and notice the instability of MnX3 (X = Cl, Br, I). The high I3 for Mn means that Mn3+ can oxidise the halide ions to halogens.

Also, early elements in the M2+ state will be strongly reducing. The stable dihalides therefore have an understandable pattern. Cu(II) is too oxidising to coexist with iodide, while ScX2 and TiF2 disproportionate to metals and trihalides.

Thermodynamic Features and Trends

The Stability of the ½ Filled Shell

The special properties of the d5 configuration are usually attributed to the “special stability of the half-filled shell”. This is an inadequate statement. “Stability” is always relative and indicates the sign and magnitude of ΔGo for some change.

d5 is usually stable with respect to d4 because of the large positive enthalpy associated with the ionisation (e.g. I3), so that ΔGo is likely to be positive, e.g.

MnCl2 + ½Cl2            MnCl3

However, d5 is also stable wrt d6 because of the much smaller enthalpy of ionisation of the d6 ion (no exchange stabilisation of the sixth electron), that can be offset by other exothermic components of the reaction, such as increased lattice enthalpy, e.g.

FeCl2 + ½Cl2 → FeCl3.

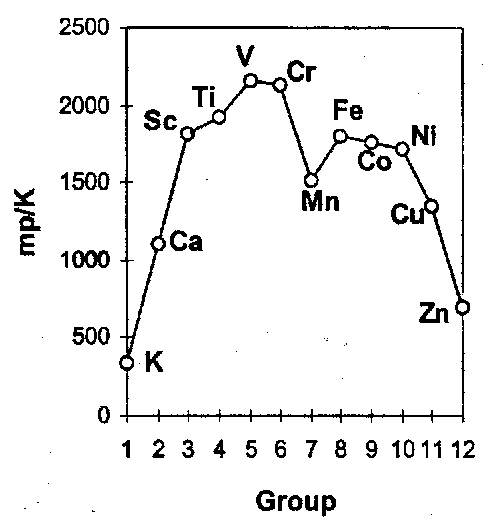
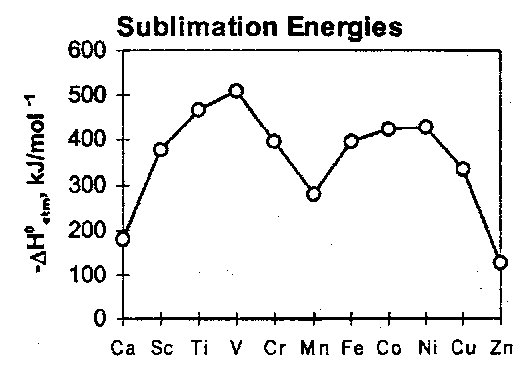
Atomic Sublimation Energies

The heats of formation of TM compounds depends on these. The melting points of the elements follow a distinctive pattern.

They are a measure of the metallic binding and mirror the atomic sublimation energies. The “double-hump” shape is a composite of:

1. the maximisation of the number of bonding electrons in the s and d bands at the centre of the series, and
2. the gain in exchange energy when e.g. the d5 atom is freed from the lattice.

The participation of the valence electrons in the metallic binding randomises their relative spin and so increases the electron-electron repulsion relative to the exchange stabilisation energy available in the free atom. The second factor is largest for atoms with the largest numbers of unpaired spins, i.e. at the centre of the series, and leads to a dip in the sublimation energy at that point.

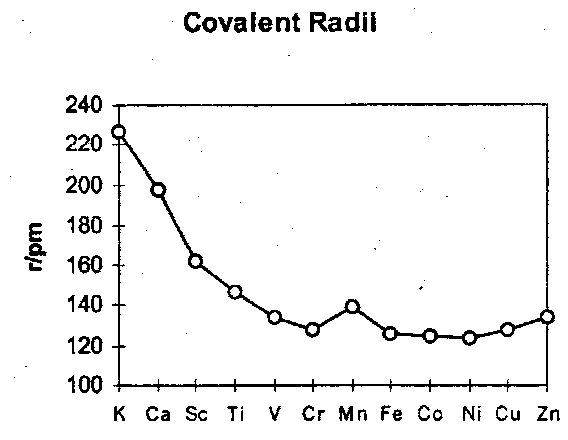
Changes in bond energy are accompanied by bond-shortening, superimposed on general contraction in atomic size.

Since density depends on r-3 and the atomic mass increase by ~30% across the series, the density rises sharply.

Stability of the +2 Oxidation State relative to the Metal

The dichlorides and oxides of the early TM’s are formed more exothermically than those of the later elements. The dominant difference is in the ionisation energies which more than offset those in the heat of formation of the gaseous atoms. This difference is only partially offset by the larger lattice enthalpies at the end of the series due to the smaller size of the cations.

The same factors apply to the redox potentials, except that we now need the hydration energies of the cations and to remember that the potential is a measure of the free energy change per electron transferred, relative to the hydrogen electrode process, i.e. a positive E0 indicates a reduction by H2 could proceed spontaneously.

The Frost Diagram plots nE0 versus the change in oxidation number, and so gives a line with a slope which is a visual indication of E0. A positive slope indicates a process in which the redox couple is much more oxidising than the H2/H+ couple, and a negative slope indicates a couple that could lead to the reduction of H+ to H2.

We see that Ti2+ (aq) is a strong reducing agent and cannot be reduced by H2; nor can Ti3+(aq), but the latter can be made by H2 reduction of TiO2+(aq). By contrast Cu+ and Cu2+ are easily reduced. The reason is the much larger heats of formation of the cations at the end of the series. The increased stability of the bulk metallic elements is referred to as nobility, and is shared by Ni, Pd, Pt, Ag and Au, as well as Rh and Ir (all late TM’s) for the same reason.

Heats of Formation of Halides and Oxides

M(II) oxides, chlorides and fluorides all show decreasing stability across the series. The contributing factors are ΔHf of the M2+ ions and the lattice enthalpies of the compounds. The difference in the lattice enthalpies at the beginning and end of the series can be got from the Kapustinskii Equation. The smaller radius of Cu2+ compared to Ti2+ predicts a lattice enthalpy that is ~130kJ mol-1 more exothermic for the Cu2+ dihalides, so the fact that the experimental values are ~300kJ mol-1 more endothermic is entirely attributable to the difference in ΔHf of the M2+ ions, and that is dominated by ionisation energies.

Heats of formation rise sharply with oxidation state, the increase in ionisation energy being more than compensated for by the increased lattice enthalpy of a compound containing a more highly charged and smaller cation (Kapustinskii).

This reaches a limit in the very high oxidation states, and the stability starts to fall off. For example CrO3 is unstable wrt CrO2 + O2, and Mn2O7 is an explosive green oil, mp 5.9oC, which detonates at 95oC, losing its oxygen in a hurry. It is claimed that FeO4 can be made in CCl4 solution, but it has never been isolated. Extrapolating from the properties of Mn, the conversion to Fe2O3 and O2 is likely to be highly exothermic, and an attempt at isolation would be unwise. Notice the decrease in stability across the TM series extends to all oxidation states.

The higher oxidation state compounds are of course highly covalent, so their instability is related to the strength/weakness of the covalent bonds. The ‘d’ orbital radii contract relative to the core as the formal charge on an ion increases, and inhibiting the overlap that stabilises covalently bound species. These factors underlie the pattern of stable oxidation states of the 1st TM series.

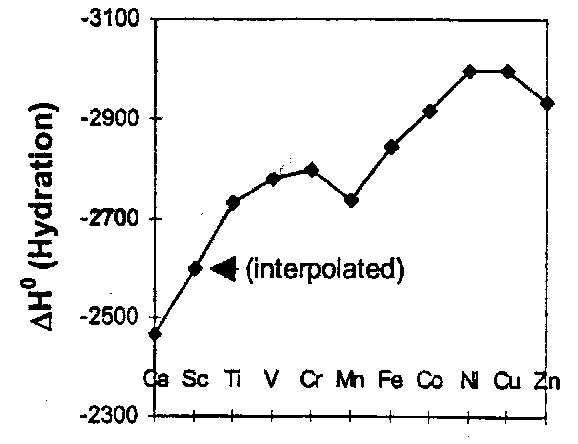
Heats of Hydration

Electrode Potentials depends on the sublimation energies, the ionisation energies, and the heats of hydration. Naively these should scale as 1/r, and because r contracts a Zeff increases, we predict an approximately linear increase across the series. This is not found.

Ca2+, Mn2+ and Zn2+ show an approximately linear relationship. All the other aquated ions have a larger heat of hydration than expected, and these differences are attributed to the occupation of the d orbitals and their angular properties. Notice that they are of the order of 100kJ mol-1, and are very small compared to the absolute magnitude of the hydration enthalpy, or even the difference between the hydration enthalpy at the beginning and end of the series (~500kJ mol-1).

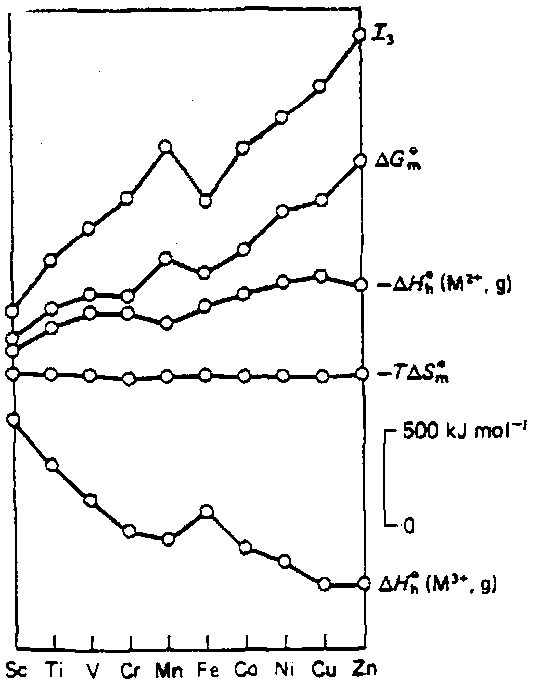
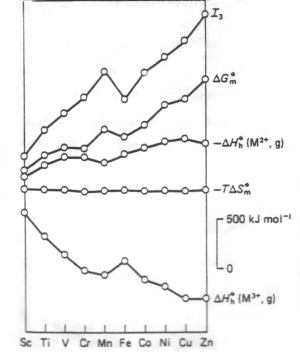
The combination of the heats of hydration of M2+ and M3+ with third ionisation energy, together with the entropy changes, gives the free energy change for the oxidation M2+ → M3+ + e-. The diagram on the right shows the relative contributions. Notice how the 3rd ionisation energy dominates the outcome. The ligand field effects have a relatively minor influence.

Now compare ΔG0 for the M2+ → M3+ oxidation from Ti to Co with the measured magnitude of the reduction potential E0, which is the proportional to the negative of the free energy of reduction. Agreement is excellent. Notice that all negative couples indicate M2+ unstable wrt H2 and all couples > 1.23V indicate M3+ will oxidise water. So Fe3+/Fe2+ is the only couple where both oxidation states coexist as a stable mixture in water at pH 0.

Ligand (or Crystal) Field Effects

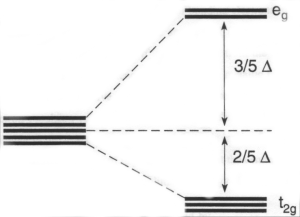
When a TM ion is surrounded octahedrally by 6 negative charges, the potential energy of electrons in the d-orbitals rises. This potential is given by 1/4πεor, where r is the distance between the electron and the ligand charge. On average this distance is smaller for an electron in the dx2-y2 and dz2 orbitals than in the dxz, dyz and dxy orbitals, so the degeneracy of the orbitals is removed. Relative to a spherically uniform distribution of the 6 negative charges, the energy of an electron in the former pair of orbitals is raised, but the energy of an electron in the other three orbitals is lowered. The two sets are usually described by Group Theory labels.

This Crystal Field splitting of the d-orbitals is responsible for subtle variations in the thermodynamic and kinetic properties of the TM ions, as well as physical properties.

The repulsive electron-ligand potential energy is just one contribution to the Born-Repulsion energy term in the Born-Lande expression for the lattice energy of a solid. When electrons occupy the t2g orbitals but not the eg orbitals, the equilibrium bond distance is shorter and the lattice energy is larger. The extent of this depends on the number of d electrons. The energy gained by this deviation is called the Ligand Field Stabilisation Energy.

Assuming fully High Spin configurations are adopted to minimise electron pairing, the trend in LFSE fits the hydration energy data, and the lattice energy of MCl2.

The ionic radii follow the expected pattern, but in some cases however, the ligand field is strong enough to overwhelm the e-e repulsion. This is the low spin case, which generates more CFSE and shorter metal-ligand distances.

Molecular Orbital Model

Many ligands are uncharged, but still have large ligand field effects, so the electrostatic model must be inadequate. Instead consider the eg orbitals whose lobes are axially symmetric about the metal-ligand bonds. They can form σ-bonds, and are sometimes called dσ orbitals. The t2g orbitals have an angular node along the metal-ligand direction, so can only form π-bonds to ligands with orbitals of π-symmetry relative to the M-L bond. Since metals are electropositive, the atomic d-orbital energies always lie above the ligand orbital energies, and thus in the MOs formed by their overlap, metal d character predominates in the antibonding MOs, and ligand p-character in the bonding MOs. σ-overlap always exceeds π-overlap, so the antibonding eg MOs are raised in energy more than the antibonding t2g MOs. The result is the same splitting pattern as from the electrostatic repulsion of negative charges at the ligands positions.

More Detail on this theory, as well as MO Diagrams, can be found in the notes on MO Theory and Bonding.

Tetrahedral Fields

In the tetrahedron the ligand field splitting is inverted, and the LFSE follows a different pattern. The table summarises these.

Configuration	Octahedral LFSE	Tetrahedral LFSe
d1	2/5 Δ	3/5 Δ
d2	4/5 Δ	6/5 Δ
d3	6/5 Δ	4/5 Δ
d4	3/5 Δ	2/5 Δ
d5	0	0
d6	2/5 Δ	3/5 Δ
d7	4/5 Δ	6/5 Δ
d8	6/5 Δ	4/5 Δ
d9	4/5 Δ	2/5 Δ
d10	0	0

Δ is smaller in tetrahedral sites. Electrostatic theory say Δtet ≈ 4/9Δoct. This appears to be quite a good approximation to the experimental ratio.

Spinels

These are closed packed oxides with formula AIIBIII2O4. Normal spinels have B in half the octahedral holes and A in 1/8 of the tetrahedral holes. In an inverted spinel, half of the B’s swap their site with the A ions. The origin of this is the difference in the ligand field stabilisation of different configurations in different symmetry sites. Assuming Δtet ≈ 4/9Δoct and Δ(M3+) ≈ 1.5Δ(M2+), which is often about right, we can calculate which spinels will be normal and which inverted from which has the largest LFSE. The table shows this calculation for Mn3O4, Fe3O4 and Co3O4. Experiment shows that Fe3O4 (magnetite) is the only one that is inverted, which is just what the calculations predict.

Factors Determining Δ 

When looking at experimental values of Δ, we notice:

1. The dependence on oxidation state.

This can be understood by the dependence of MO bonding on the energy difference between atomic orbitals. Since the ligand valence orbitals usually lie below the metal orbitals, an increase in metal oxidation state brings the d-orbital energy closer to that of the ligand, and increases the interaction.

 

2. A factor of about 1.5 between the 1st row and 2nd row, and a further 1.5 between 2nd and 3rd rows.

This can be explained in terms of the increased overlap of the d-orbitals that follows from the larger average radius of the 4d and 5d shells in relation to their cores.

3. The strong dependence on ligand type.

There is no correlation with ligand charge. The analysis depends on the σ and π bonding properties of the ligands.

Ligands which bind via σ bonds alone (e.g. NH3) have intermediate values of Δ cause by the antibonding character of the eg orbitals.

Ligands with filled π-orbitals (F-) also give the t2g orbitals antibonding character and reduce Δ.

Ligands like CN- have empty π* orbitals due to their internal double bonding, and lie somewhat above the metal d orbitals. The result is that the t2g orbitals take on a bonding character and are lowered in energy, thereby increasing Δ.

Stereochemical Preferences

The common geometries for mainstream coordination compounds of the TM’s are octahedral, tetrahedral and square planar. The first two minimise repulsion between ligands, but the latter indicates directional bonding. It is a common mistake to assume that the coordination depends on differences in LFSE. Most tetrahedral coordination occurs with ligands that are very bulky, or carry negative charge. Octahedral complexes of the type MIIX64- (X = halide) are unknown, due to the prohibitively large electrostatic repulsion energy between halide anions. Instead tetrahedral complexes MIIX42- are preferred.

This happens for many metals including Mn and Zn, neither of which have any LFSE. In water the halide complexes have low formation constants, but the exception is CoX42-; the d7 configuration is that which has the most favourable change in LFSE in passing from the octahedron to the tetrahedron. LFSE is most likely to influence stereochemistry when the ligands are high in the Spectrochemical series, e.g. CN-, so Ni2+ forms square planar complexes with this ligand and others like it.

Geometries

Low coordination number, e.g. CN = 2 are linear, e.g. [AgCl2]-. These are often metals such as Cu(I), Ag(I), Au(I), because they favour low oxidation states (due to high ionisation energies as they are small) and they have strong covalent tendencies due to class-b character. These later Group metals favour the lower oxidation states because the d orbitals decrease in energy across the period, so they are essential core-like electrons by the time you reach Group 11. CN = 3 is rare, but several examples are known.

Tetrahedral – CN=4. This is favoured when the central atom is small and ligands are large, because of ligand-ligand repulsions, e.g. [CrO4]2-.

Square Planar – CN=4. Typically d8 metal, e.g. [Ni(CN)4]2-. It is also commonly formed by 2nd /3rd row metals which are 4-coordinate. This is because the bonding orbitals are lower in energy and give a better energy match and overlap, which allows for strong directional bonding. For 1st row metals, this directional bonding requires large LFSE, so a good ligand capable of making up the energy loss. d8 favours this because of orbital occupation.

Five Coordinate – less common square pyramidal and trigonal bipyramidal. The latter gives less steric repulsions, but polydentate ligands often adopt the former. The energy difference is minimal though, e.g. [Ni(CN)5]3- switches between. This fluxionality also occurs for 8 coordination.

Octahedral – very common, e.g. [Fe(CN)6]3-. It is favoured because the more M-L bonds formed the better energetically (stabilising orbital energies), but 6-coordination does not usually lead to strong steric crowding, and the subsequent repulsions that would destabilise it.

Higher Coordination – 2nd and 3rd row metals are large enough to fit more ligands around them without adverse steric factors.

To determine the coordination and geometry, it is useful to consider:

Sterics – electrostatic repulsion between large ligands.

Electronic – more M-L bonds confers Energy gain. MO Theory – strength of ligand.

Crystal Field – splitting of d-orbitals by (charged) ligands capable of reducing or increasing repulsion due to location of electrons.

Of these, the first two factors dominate in deciding, while Ligand Field Stabilisation is a small effect.

For example, large metal ions will have high coordination because sterics are reduced while M-L bonds are maximised. Conversely, large ligands and/or small ions reduce coordination number.

LFSE will cause changes in geometry though, e.g. tetrahedral to square planar. This is where strong ligands e.g. CN- split the d-orbitals further to maximise stability.

The Jahn-Teller Effect

The Jahn-Teller Theorem states that “a non-linear molecule with a degenerate ground state is unstable with respect to a distortion that removes that degeneracy”. 

To a good approximation the spatial displacement of atoms does not affect spin degeneracy, so only the orbital degeneracy associated with electrons in degenerate orbitals matters. In the octahedron such degeneracy is found in the configurations: t2g1, t2g3, t2g4, t2g5, eg1, and eg3. Equivalent degeneracies exist in the tetrahedron.

Not all the configurations lead to observable distortions. The theorem does not say anything about the magnitude of the favourable energy change that occurs in the course of the distortion. If this is much smaller than kT, i.e. typical thermal energies, then the molecule will not be trapped in a potential energy-well centred on the distorted geometry, and most experiments will report it as undistorted. If the change in potential energy of the d electrons as the distortion progresses is large compared to bond stretching energies, then the molecule may indeed end up with a static distortion.

The sensitivity of the eg orbital energies, which are σ-antibonding, to ligand displacements is much larger than that of the t2g orbitals, which are weakly π-antibonding, so in practice the only configurations which give rise to static Jahn-Teller distortions are eg1 and eg3. the main examples come from the d4 high-spin and d9 configurations, corresponding to Cr2+ and Cu2+. Almost all known examples of supposedly six-coordinate copper(II) (d9) compounds are tetragonally distorted, whether they be simple species like CuO or the Cu2+ ion coordinated by H2O or NH3 in solution. The same is true of CrCl2, and many Cr2+ d4 complexes.

The distortion is always an elongation along a 4-fold axis, despite the fact that the eg degeneracy is also removed by a compression along this axis. The displacement in the d-orbital energies does not explain this. However, in the presence of the either distortion, the dz2 can be mixed with the 4s orbital, just as s and pz are mixed in linear diatomic molecules. The result is an sdz2 hybrid with a much extended amplitude in the z-direction. As a result more potential energy is gained by elongation along z than in the xy plane.

Tetrahedral Copper(II) complexes are also distorted, being flattened towards square-planar in species like CuCl42-.

Stability of Oxidation States

The situation in aqueous solution can be summarised in a Frost Diagram.

There are many points to notice:

• Most data are at pH = 0, but the triangular data points are at pH = 14.
• The trend across the transition series is for all redox couples to become more oxidising, this is primarily due to increasing ionisation energies.
• Slopes more positive than O2/H2O mean that the higher oxidation state oxidises water, so Mn3+ and Co3+ are not stable in water at pH 0. Attempts to prepare higher oxidation states of say Co, Ni and Cu, not shown in the diagram, fail for the same reason. Conversely all M2+ from Ti to Fe (other than Mn2+) are unstable wrt air oxidation to the M3+ ions.
• All the metals will generate H2 at pH 0, except copper. Note the odd position of Zn, which is due to the low ionisation energies of the 4s electrons compared to the 3d.
• The data points shown in alkaline solution indicate that the couples are less oxidising in this environment. Indeed it is only for this reason that FeO42- can be prepared in aqueous solution.
• All the high oxidation state species are either oxycations, or oxyanions.

Redox Equilibria

ΔG = F Eo(M3+/M2+)

ΔG = ΔH – TΔS

This gives:

ΔG = I3 + ΔHL(M3+,g) – ΔHL(M2+,g) – TΔS + ΔHH

Now look at trends for these quantities:

• Variation of TΔS is negligible.
• ΔHh(M3+)–ΔHh(M2+) is very small compared to I3. They both depend on r, which decreases across the period. Resulting changes more dramatic for M3+ because this also depends on Z2.
• LFSE – too small an effect except V→Cr, where decrease is due to t2g3 → t2g3eg1 (antibonding).

Key factor that this dominates is I3, the 3rd ionisation energy. It follows from its variation that ΔG increases across the period (in general).

This is because I3 is linked to radii, which decrease (so I3 increases) across the period as d-electrons do not adequately shield for increasing Z.

There is a drop from Mn to Fe because I3 also depends on the Exchange Energy values. This normally follows a regular pattern as electrons add and pair up, but for d6→d5 there is little change in this value, so I3 drops (as does ΔG).

Thus, E(M3+/M2+) increases across first row.

This links directly to the halides, since the ΔH values convert to lattice enthalpies, UL.

MX2 + ½ X2 → MX3

ScCl3 stable. TiCl2, VCl2, CrCl2 are stable. MnCl2 is stable but never MnCl3.

FeCl3 very stable (corresponds to drop in I3).

Subsequent rise in I3 again increases ΔG, so MX3 unstable for Co to Zn.

As the halide gets larger, MX3 tends to be more unstable.

X=F → more stable due to easier F-(g) formation and increased UL.

The Effect of pH

In aqueous solution an important factor is pH. In the Nernst Equation:

[Ox] and [Red] are a shorthand for the product of all the activities raised to the appropriate power, on the oxidised and reduced side of the equation for the half-reaction, and may well include the H+ concentration. Take as an example the V(V) / V(IV) reduction couple VO2+ + 2H+ + e- → VO2+ + 2H2O, for which E0 = +1.0V at pH 0. At pH 14 the factor [H+]2 on the oxidised side changes by 10-28, so the Nernst equation gives E = E0 + (0.059 x -28) = -0.652, and we find that V(IV) is a strong reducing agent. Indeed in alkaline solution air easily oxidises vanadium to VO43- which is the stable species at pH 14.

There are numerous examples of this pH sensitivity. MnO4- is a very strong oxidising agent in acid solution but only a mild one in alkaline solution. Fe3+ oxidises I- to I2 in acid solution. In alkaline solution the main species present are Fe(OH)2 and Fe(OH)3 both of which are insoluble. However because Fe(OH)3 is much more insoluble than Fe(OH)2, the activity of Fe3+(aq) in equilibrium with the solid hydroxide is very much smaller than the activity of Fe2+(aq). The change in the Fe(III) / Fe(II) couple is sufficient to allow I2 to oxidise Fe(II) to Fe(III); exactly the opposite of what happens in acid solution.

Broadly speaking, the higher oxidation states of the transition metals have a stronger association with oxide or hydroxide ions, due to more extensive hydrolysis reactions associated with more highly charged cations. This means that reduction is usually accompanied by the protonation of oxide or hydroxide to give water, and it is the free energy of this process which determines the pH dependence. Note the general feature that high oxidation states are stabilised in alkali, and low oxidation states are stabilised in acid.

A map of redox stability conditions in water is called a Pourbaix Diagram (right).

The common oxidation states of iron give a good example. Lines in this diagram indicate regions where the activities of the species on either side of the line are equal, and the areas regions where one species is dominant. Horizontal lines indicate half-reactions with no pH dependence. Vertical lines separated aquated ions from the insoluble hydroxides at a point determined by the solubility product of the hydroxide. Notice that Fe(OH)3 is precipitated at pH 3 but Fe(OH)2 is precipitated at pH 6.5. The slope of the boundary from the Nernst Equation applicable to the process:

Fe(OH)3 + 3H+ + 3e- → Fe2+ + 3H2O

Accordingly E should increase by (3x0.059/1) = 0.18V for each unit decrease in pH. This is confirmed by the diagram. Notice how the area of stability of Fe(III) extends progressively to more negative potentials as the pH increases, i.e. progressively weaker oxidising agents are needed to oxidise Fe(II) to Fe(III). The I2/I- couple has E0 = 0.536V, so we see that it can perform this oxidation at any pH > -3, but that in more acidic solutions Fe3+ oxidises I- to iodine.

Effect of Ligands on Redox Couples

Couples can change drastically with the nature of the coordinated ligands. Ligands that are good π-acceptors stabilise low oxidation states, because back-donation is more significant, due to a closer energy match of the metal orbital and ligand π* orbitals. This makes the higher oxidation state more oxidising and the potential more positive.

Conversely ligands which are good σ (and possible π) donors stabilise high oxidation states, because of the closer energy match of the donor orbitals and the empty orbitals on the metal. EDTA is an example of this.

These are all enthalpy arguments. However, redox potentials are proportional to free energy changes, which include entropy terms. An important part of the entropy change in the redox process from the change in the degree of ordered water around the complex. Thus a reduction of Fe(phen)33+ to Fe(phen)32+ leads to an positive entropy change as more solvent ordering occurs around the former ion. This makes the redox potential more positive. On the other hand the reduction of Fe(CN)63- to Fe(CN)64- generates a species of higher charges so that the entropy change is negative, which in turn makes the redox potential more negative. Thus a compromise develops between the enthalpic effect of the π-acceptor CN- ligand stabilising the low oxidation state and the salvation entropic factor that operates in the opposite direction.

Even more dramatic effects are found in cobalt chemistry. An important example is the contrast between Co(H2O)63+ / Co(H2O)62+ where E0 = +1.84V but Co(NH3)63+ / Co(NH3)62+ has E0 = -0.10V. in both cases the Co(III) species are low spin d6 (t2g)6, while the Co(II) species are high spin. The difference is best attributed to the degree of donor and acceptor character of the d orbitals and the ligand σ orbitals. The energy mismatch is least between the relatively high energy donor orbitals of the ammonia and the relatively low energy acceptor orbitals of Co(III), leading to the stabilisation of this species by the ammonia. The results are far-reaching. In aqueous media and the absence of strong donor ligands, Co(III) is a virtually unknown oxidation state, but in the presence of ammonia or similar ligands Co(II) is easily oxidised to Co(III) for which a prolific series of compounds is known. The enormous number of coordination compounds of Co(III) is also due to their slow kinetics of the substitution reactions of this oxidation state, which is attributable to the t2g6 configuration.

Comparison of the 1st with the 2nd and 3rd Transition Series

Atomic Radii and Ionic Radii

The contraction of all radii across all the series are noted, and also the very similar radii of the second and third series elements. This is a result of the lanthanide contraction. The lanthanide elements occur before the 3rd transition series. They correspond to the filling of the 4f shell which has no radial node. The 5s, 5p and 5d have respectively 4, 3 and 2 radial nodes, showing them to penetrate the 4f shell, so the incomplete shielding of these electrons by the 4f shell leads to a contraction of atomic and ionic radii. The result is a strong similarity between the 2nd and 3rd transition series elements.

4f and 5d Valence Orbitals

These are simultaneously more penetrating (one and two radial nodes respectively) and more diffuse (larger average r) than the 3d. The greater diffuseness leads to a much reduced mutual repulsion between electrons, since they are on average further apart than in the 3d. so spin-pairing occurs more readily, because spin-correlation (exchange) energies are smaller. The increased amplitude of these orbitals outside the core results in more overlap with ligand orbitals, leading to more covalency in the bonding.

Heats of Atomisation

One result of the stronger covalent bonding is stronger bonds in the metallic elements. This can be seen in the heats of atomisation, which are much larger for the second transition series than for the first, and larger again for the third. It is also striking that the dip in the binding energy at Mn, which is explained by exchange stabilisation of the free atom containing a half-filled shell of d electrons, is more of less absent in the other two series. This comes from the reduced importance of the electron-electron repulsion in the more diffuse 4d and 5d. the result is a set of metals in the centre of the series that are very high melting, with W at 3382oC being the largest. That is why it is used for filaments that must run at high temperature.

Features of the 2nd and 3rd Transition Series

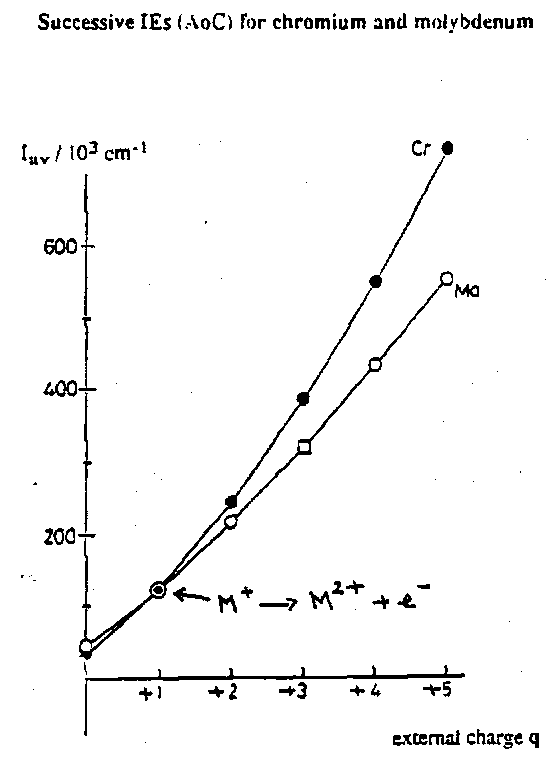
Ionisation Energies in Series 2 and 3

The main difference from the 1st Transition Series is the slower rise in successive ionisation energies. The data for Cr and Mo illustrate this. The first two ionisation energies are very similar, but thereafter the difference becomes large. Exactly the same behaviour is found in other groups. It may be rationalised by considering penetration. Recall that the ionisation of valence electrons has a much smaller impact on the binding energy of penetrating electrons, for which a sizeable contribution comes from the near nuclear region, than on the ionisation energy of non-penetrating electrons. So the 4d and 5d orbital energies are not as sensitive to the formal charge on the ion as the 3d. The outcome is a much increased stability for higher oxidation states, relative to the 1st Transition Series. High oxidation states are significantly more stable and common in the 2nd and 3rd transition series compared with the 1st.

The combination of high heats of atomisation and the stability of high oxidation states means that low oxidation states in compounds with ionic character are susceptible to either disproportionation or oxidation by water. This is particularly clear in the occurrence of ordinary aquated cations, such as M2+(aq) and M3+(aq) that we take for granted in the 1st transition series. Remember that all M2+(aq) exist for V2+→Zn2+, and also Ti3+→Co3+. The known stable aquo-cations in the other two series, makes a very brief list.

Increased Stability of High Oxidation States

This follows directly from the lower ionisation energies shown above. A good example is the heats of formation of halides of Cr and W. It is noticed that:

• Fluorides are formed more exothermically than chlorides, as expected from the ionic model.
• CrF2 is formed more exothermically than MoF2 (ionic radius of M2+), but WF6 and WCl6 are stable whereas the Cr compounds are unknown.
• WF6 and WCl6 are very covalent, and their formation is stabilised by the large overlap of the 5d orbitals compared to the 3d in Cr.

The results are the same for the oxides and are also apparent in the redox couples in water. Whereas CrO42- is a well-known oxidising agent, MoO42- and WO42- have no significant oxidising properties. This pattern is repeated in all the groups of the transition series. For example there is no aqueous chemistry of Zr other than in the IV state and none of Nb other than in the Nb(V) state. Whereas MnO4- is well-known for its oxidising properties, ReO4- is not an oxidising agent. FeO4 is unknown, but OsO4 is a stable solid, etc. etc. The redox couples for the Mn group are seen to follow those in the Cr Group.

A summary of the redox stability in water in the 2nd and 3rd transition series shows the change from the 1st transition series. Notice:

• The much flatter slopes of the couples involving high oxidation states
• The fact that most electrode potentials for the process M(s) → M2+(aq) are positive in the latter half of both series. This is largely due to the large heat of sublimation of the metals together with the large ionisation energies of the elements in this position, and explains why all the elements, Rh, Ir, Pd, Pt, Cu, Ag, Au are described as noble.

Finally, we consider the common oxidation states of the 1st Transition Series and compare them with the 3rd Transition Series. It is noted that:

• There are now very low formal oxidation states.
• Higher oxidation states are much more common in the 3rd transition series.
• In any of the groups except the first few, there are more accessible oxidation states in the 3rd transition series than in the first.

All this follows because oxidation states are an increasingly poor description of the absolute charge on the metal (which according to Pauling’s electroneutrality rule is never greater than ±1) as covalency increases. Because of the larger 5d radius, covalency is much larger in the 3rd transition series and it is therefore increasingly possible to tolerate anomalous formal charges on the metal.

Metal-Metal Bonding

Remember that the larger radius of the 4d and 5d orbitals led to higher heats of sublimation of the metal. There are also many examples of compounds, nearly always in low oxidation states in the 2nd and 3rd transition series where M-M covalent bonding is important. For example the apparently triangular molecule Fe3(CO)12 has bonds between its iron atoms, but on one side of the triangle this is supplemented by two bridging CO molecules. In Ru3(CO)12 and Os3(CO)12 the M-M bonds are stronger and these bridges are absent. The apparently innocent looking species with the empirical formula ReCl4- is not a tetrahedral unit. Instead it exists in two forms, either as Re2Cl82- or as Re3Cl123-. Both of these contain M-M bonds, the former being remarkable in containing a quadruple bond. Often metal atoms cluster together in octahedra. This happens in NbO, and in MoCl2 and in many other species.

High Coordination Numbers

Coordination numbers greater than 6 are unusual. To sustain larger coordination requires:

• A large central atom
• A high formal charge to act as an acceptor to a large number of ligands.

These are therefore normally found at the beginning of the 2nd and 3rd transition series, where high oxidation states are stable and the cations are large. Examples are species like ZrF83-, Mo(CN)83- and so on.

Low-Spin Configurations

The large radii of 4d and 5d give large ligand field splittings Δ. However the large orbitals also reduces the mutual repulsion of electrons, which opposes spin-pairing in the t2g orbitals of the octahedron. The result is that almost all 2nd and 3rd row compounds exhibit low spin configuration.

The 18 Electron Rule

π-acceptors stabilise low oxidation states. These are usually ligands with π-unsaturation associated with their own internal multiple bonds. Other examples are phosphines, etc, which have low energy acceptor orbitals, usually attributed to the d orbitals on P, etc, but which may also involve the σ-antibonding orbitals on the P-R bonds of PR3, etc. the best example are the carbonyls. The important ones in the 1st transition series all have a valence electron count of 18. This simple rule is the best general guide to the formulation of organometallic compounds and other species in low oxidation states.

The MO basis is addressed in the Organometallics Notes. The key point is the energy differentiation between the antibonding orbitals and the rest, and it is strengthened when the ligands are π-acceptors, because the non-bonding orbitals on the metal become π-bonding and are lowered in energy. The result is a large HOMO-LUMO gap.

The large HOMO-LUMO gap is vital. If the HOMO is not full the complex must be a strong oxidising agent because of the presence of a low energy empty orbital and is unstable to a reduction which fills this set of orbitals. Conversely, if the LUMO contains an electron the compound would be a strong reducing agent, and readily oxidised so that the LUMO remains empty. Both factors ensure that the total of 18 electrons is maintained.

A further important feature is the slowness of ligand replacement reactions, i.e. kinetic stability. This comes about because the high energy of the LUMO makes the complex a poor partner for attack by a nucleophilic ligand, and the low energy of the HOMO inhibits attack by an electrophilic ligand. Most reactions proceed by a bond dissociation mechanism, but the large HOMO-LUMO gap implies a large contribution to the activation energy from the rearrangement of valence electrons in the transition state, which then has a high energy. The 18-electron Rule is primarily a statement about kinetic stability.