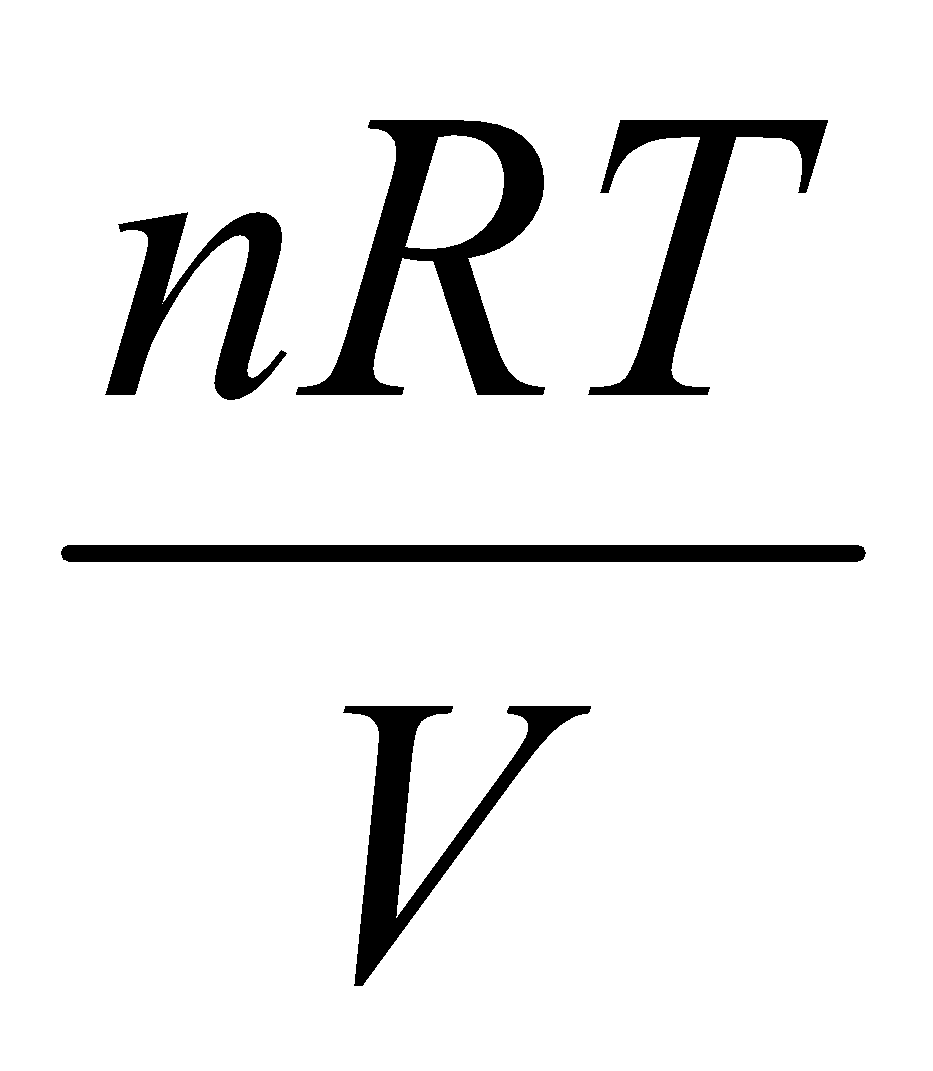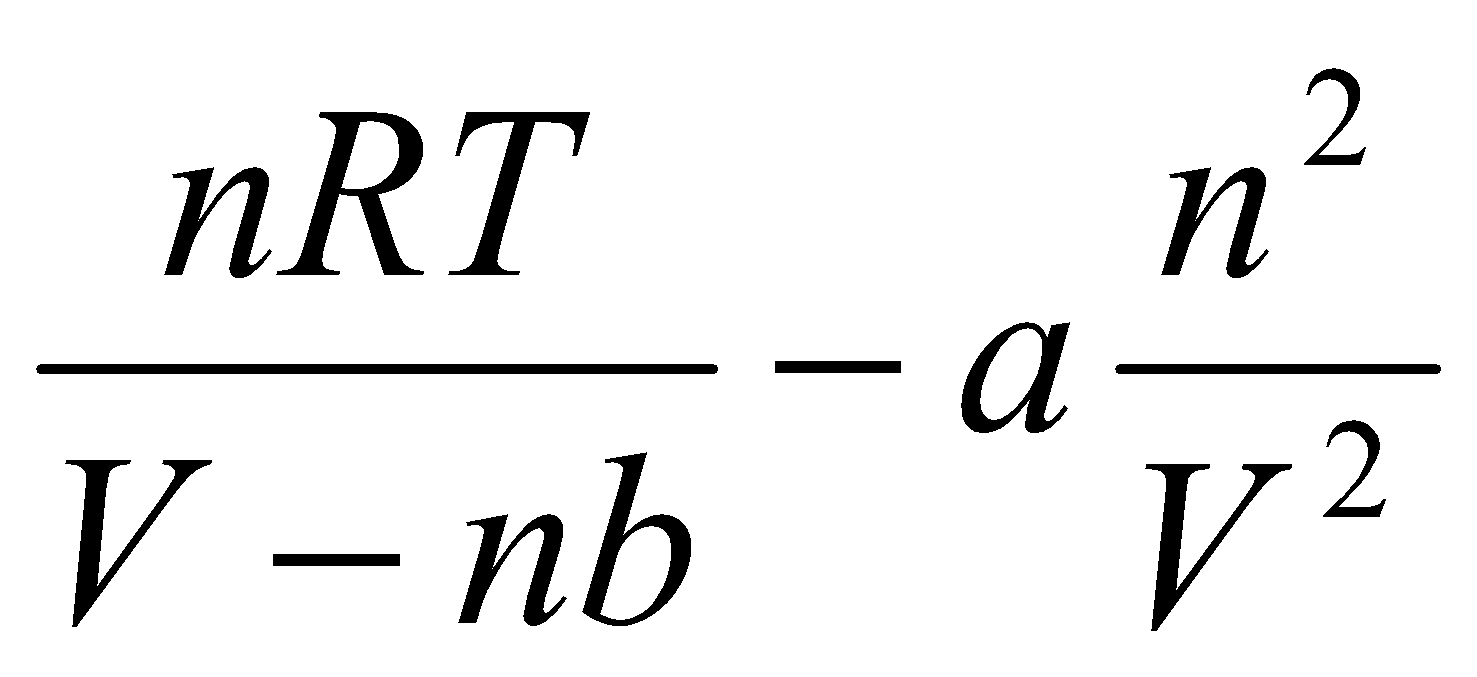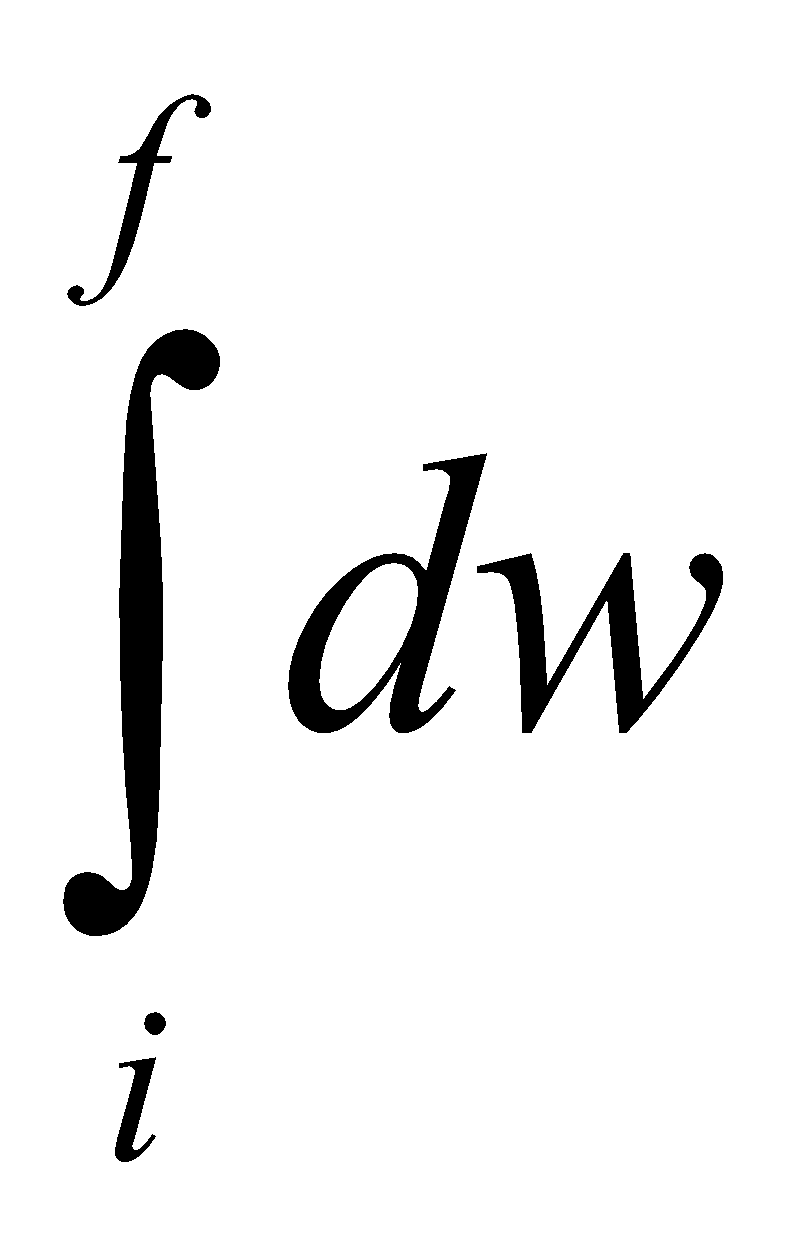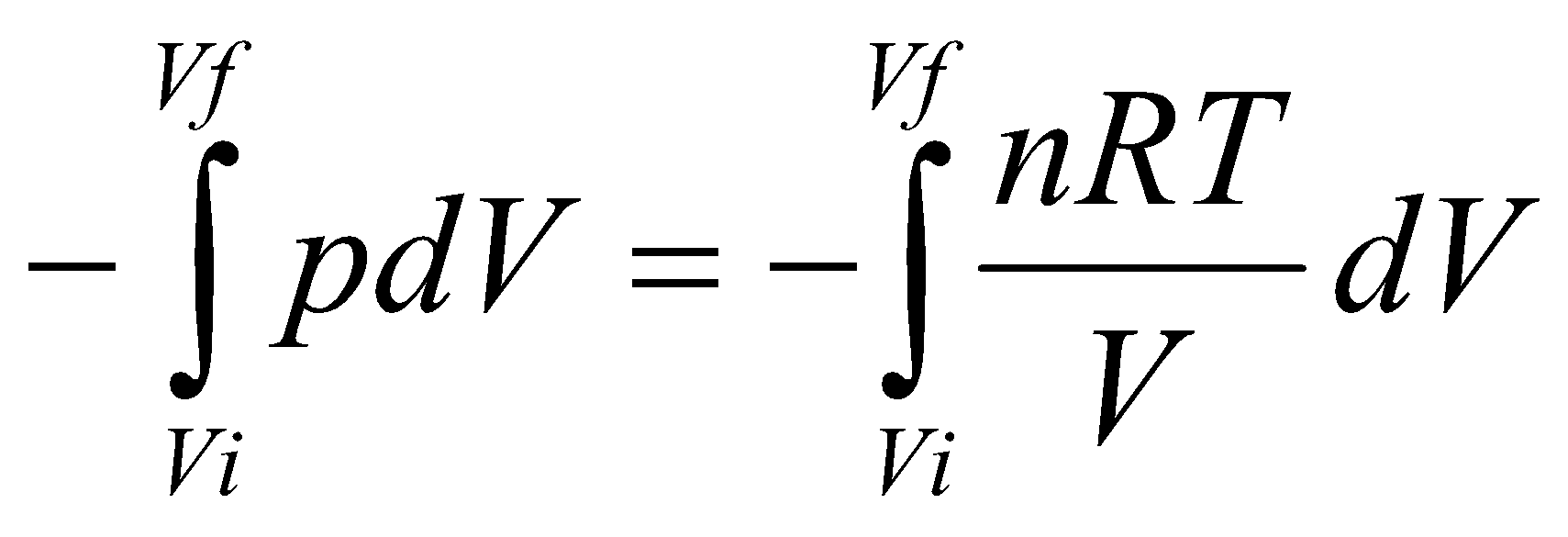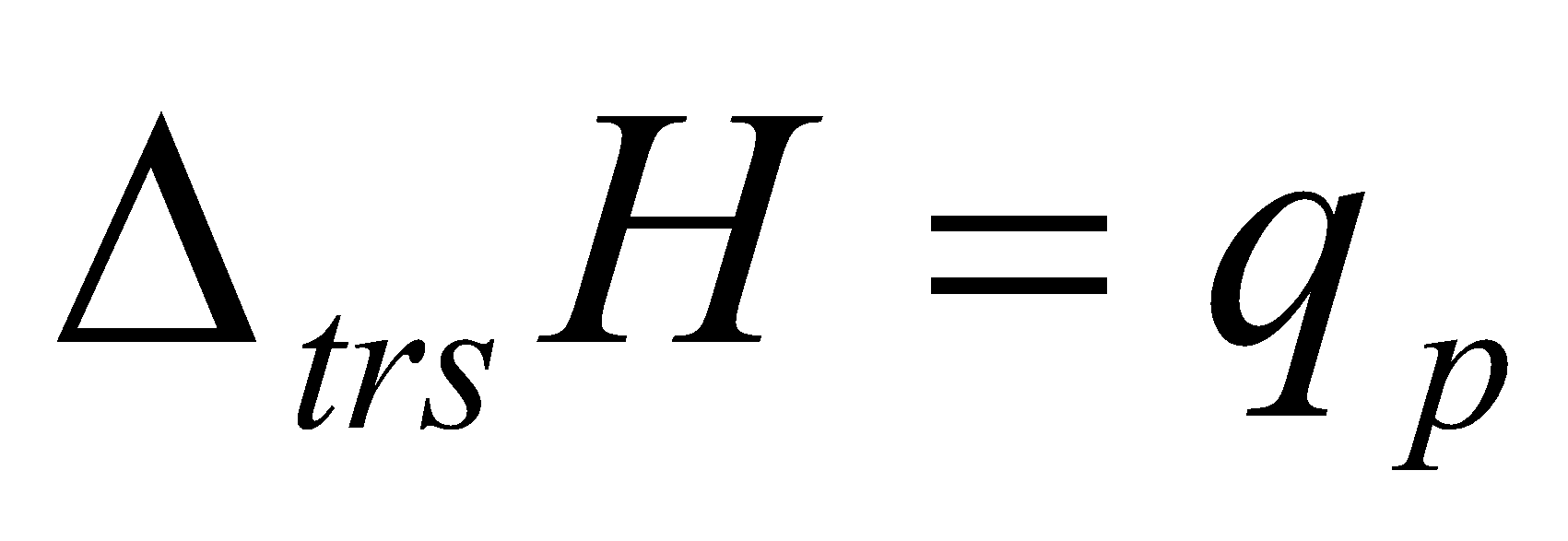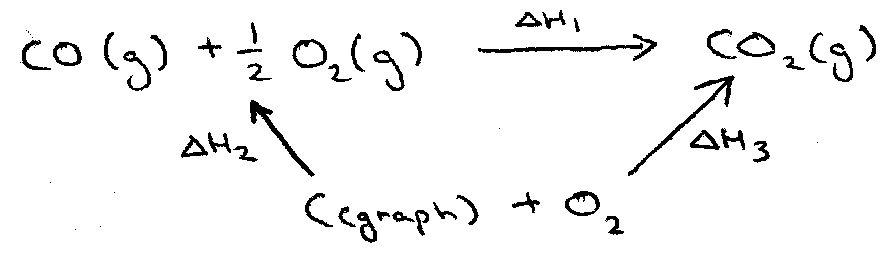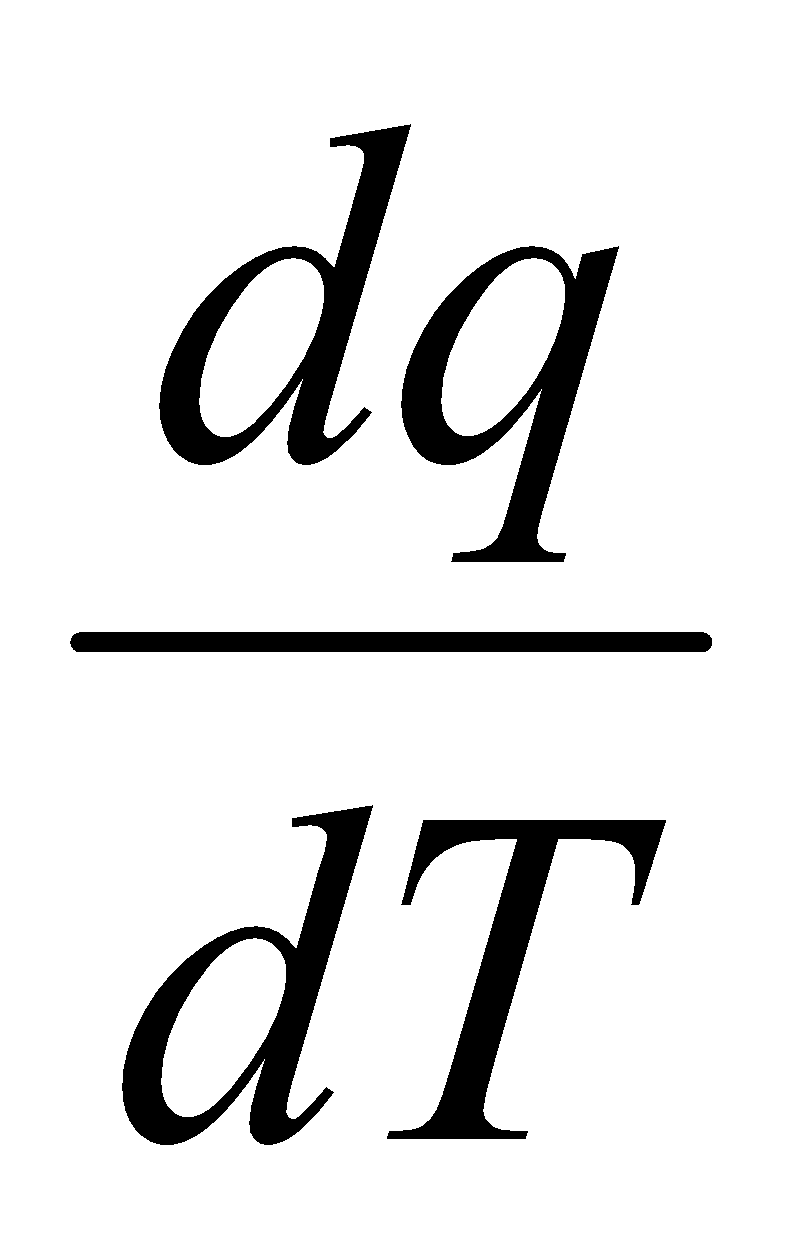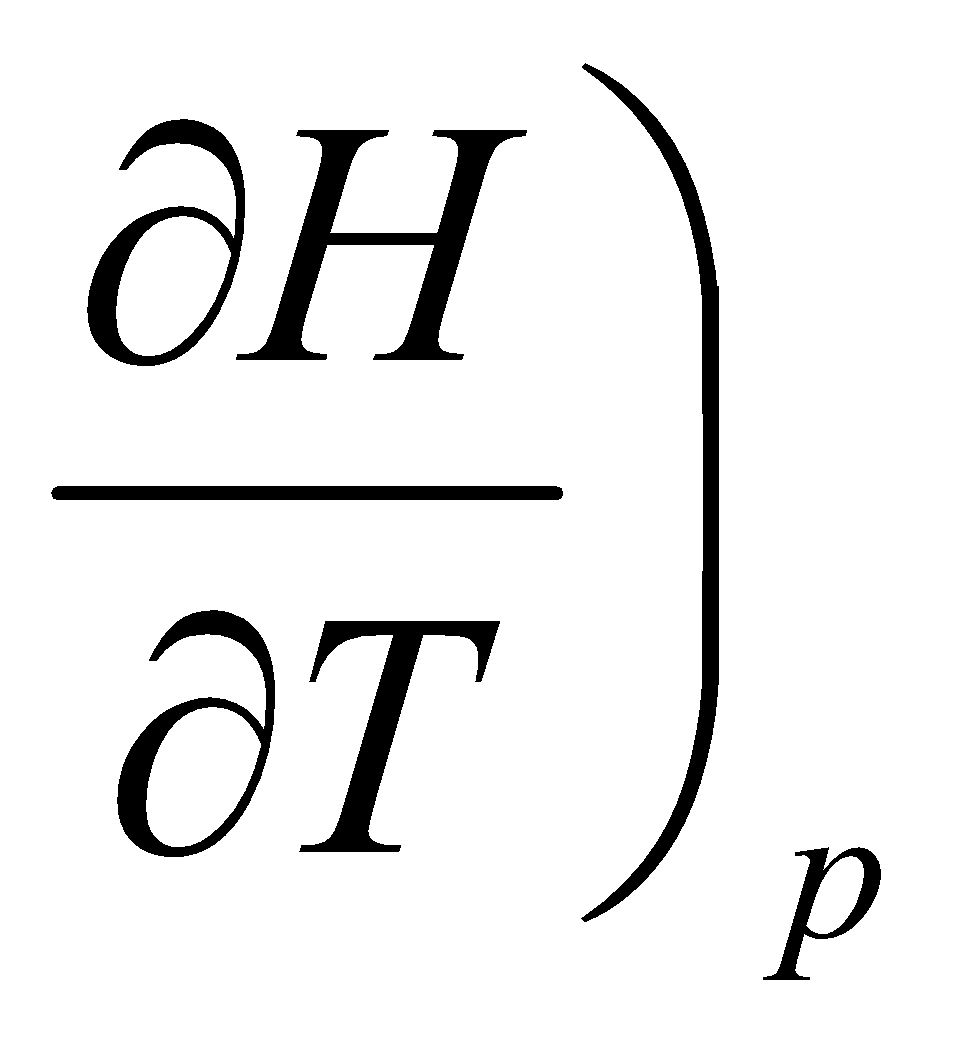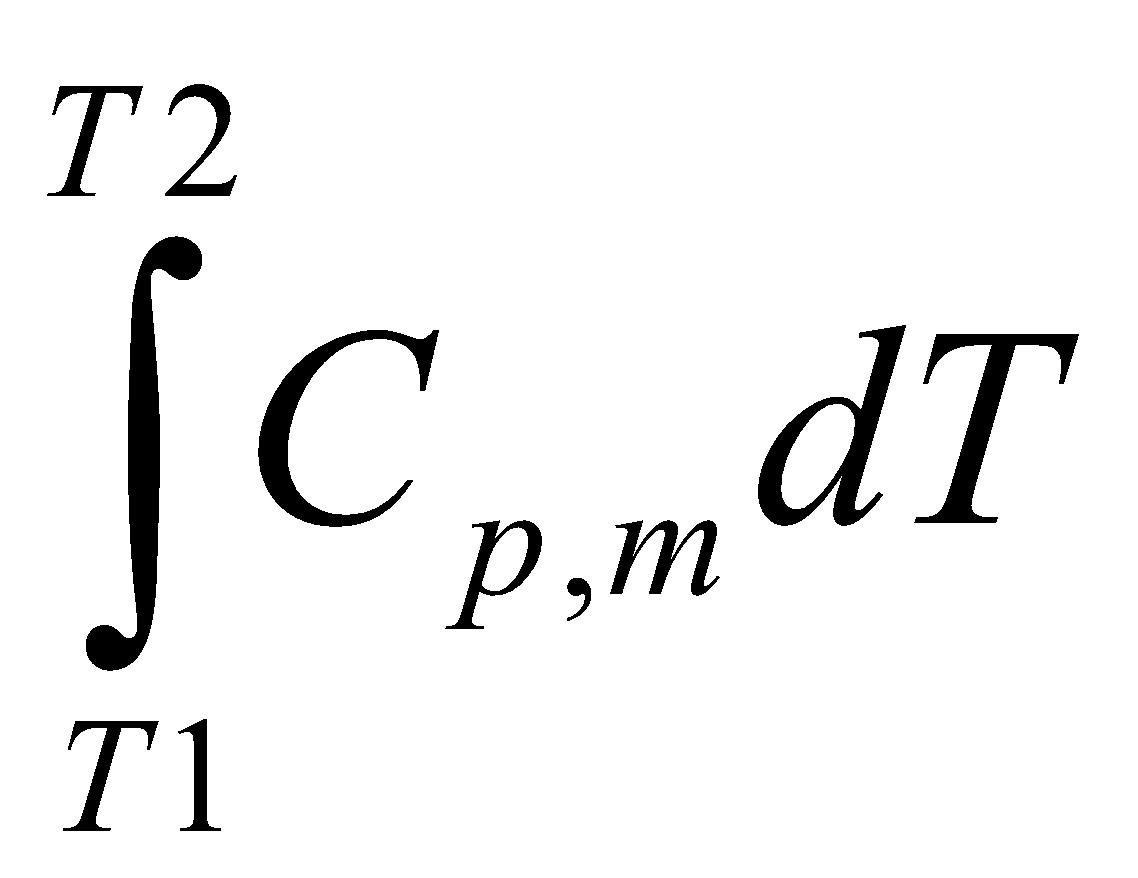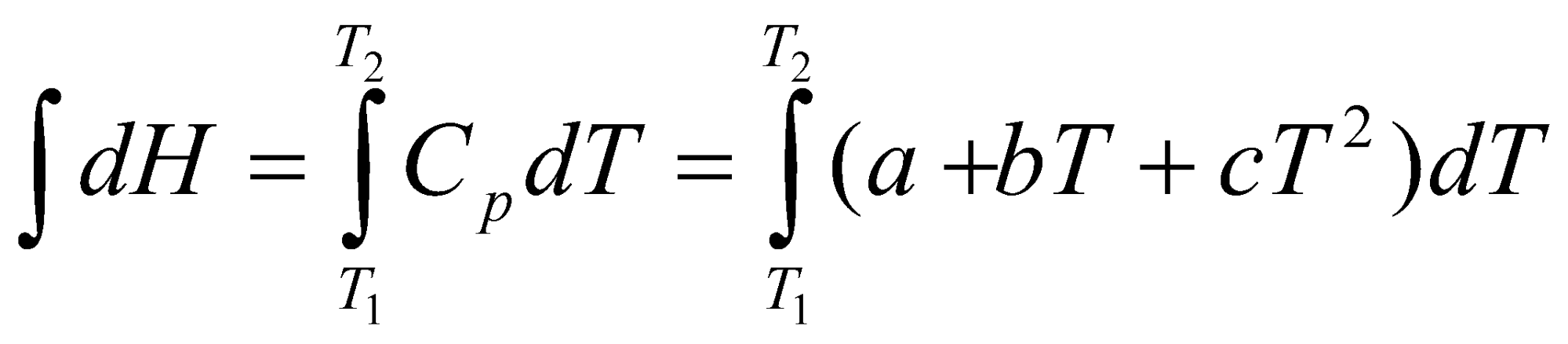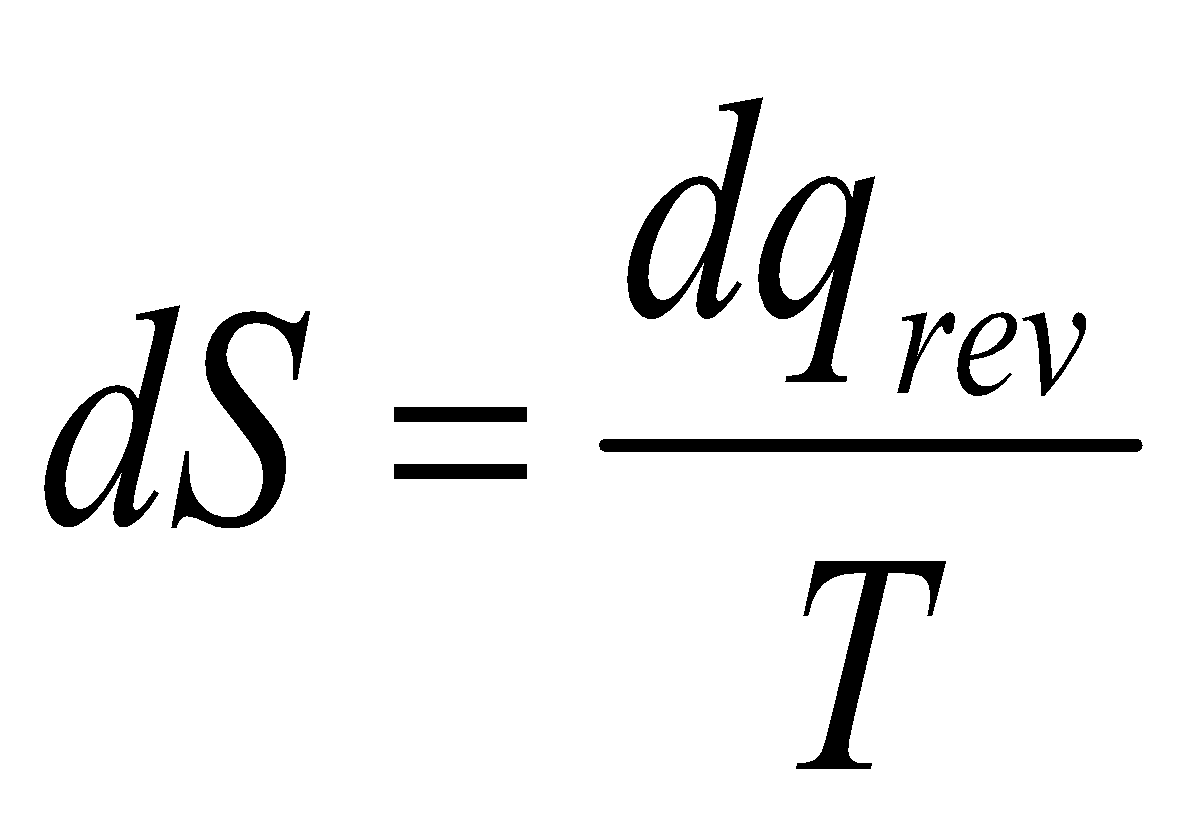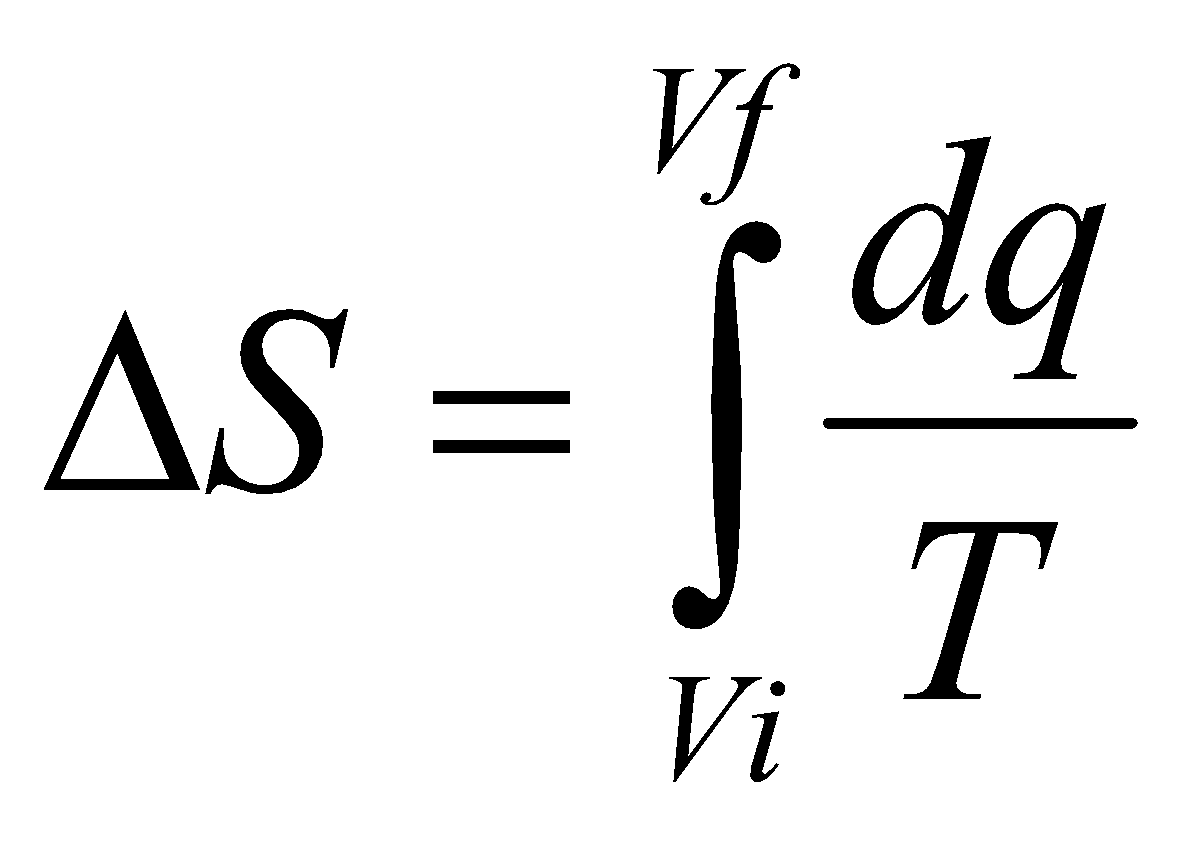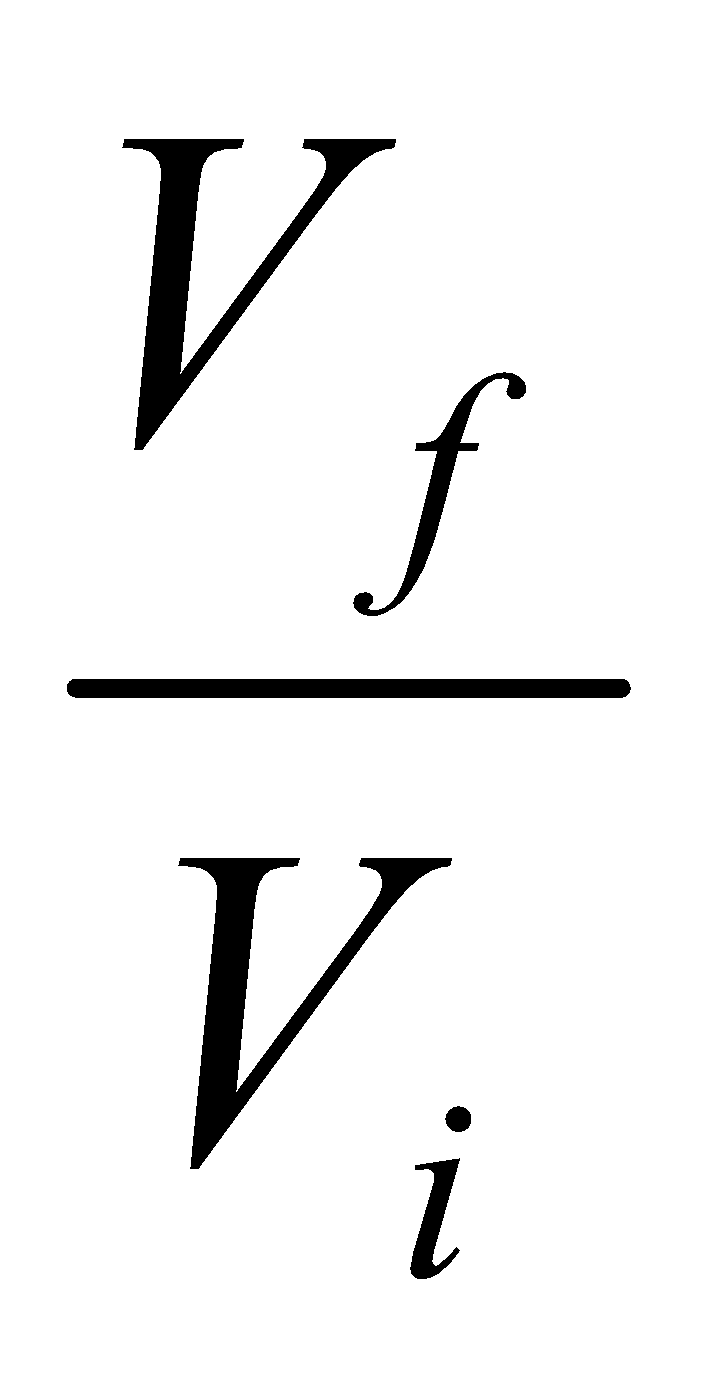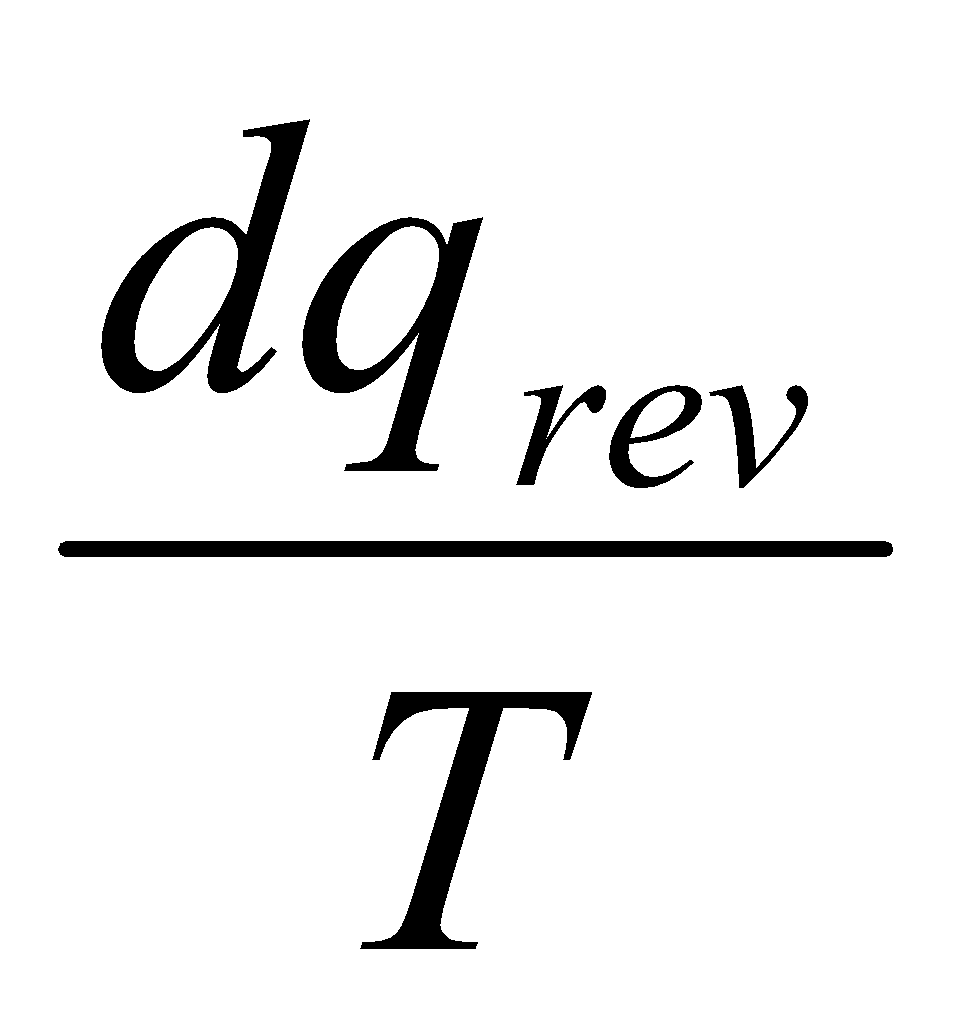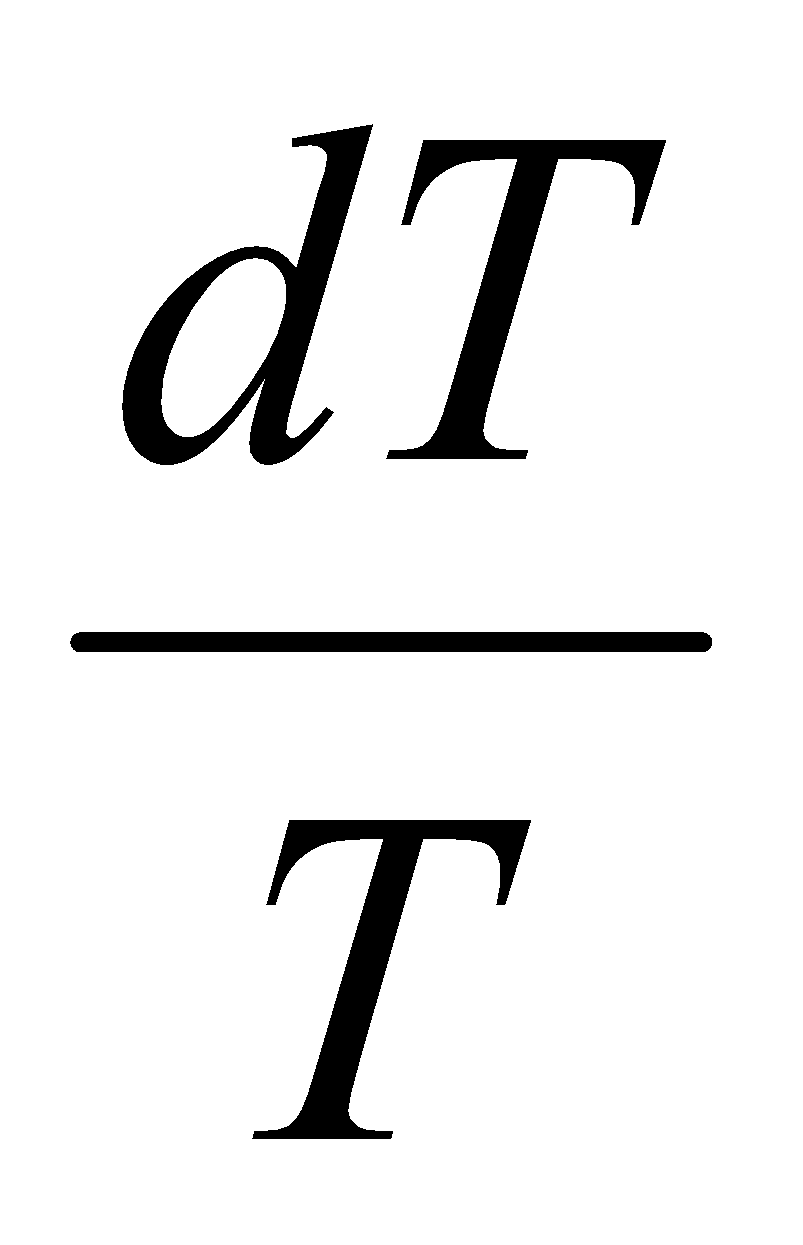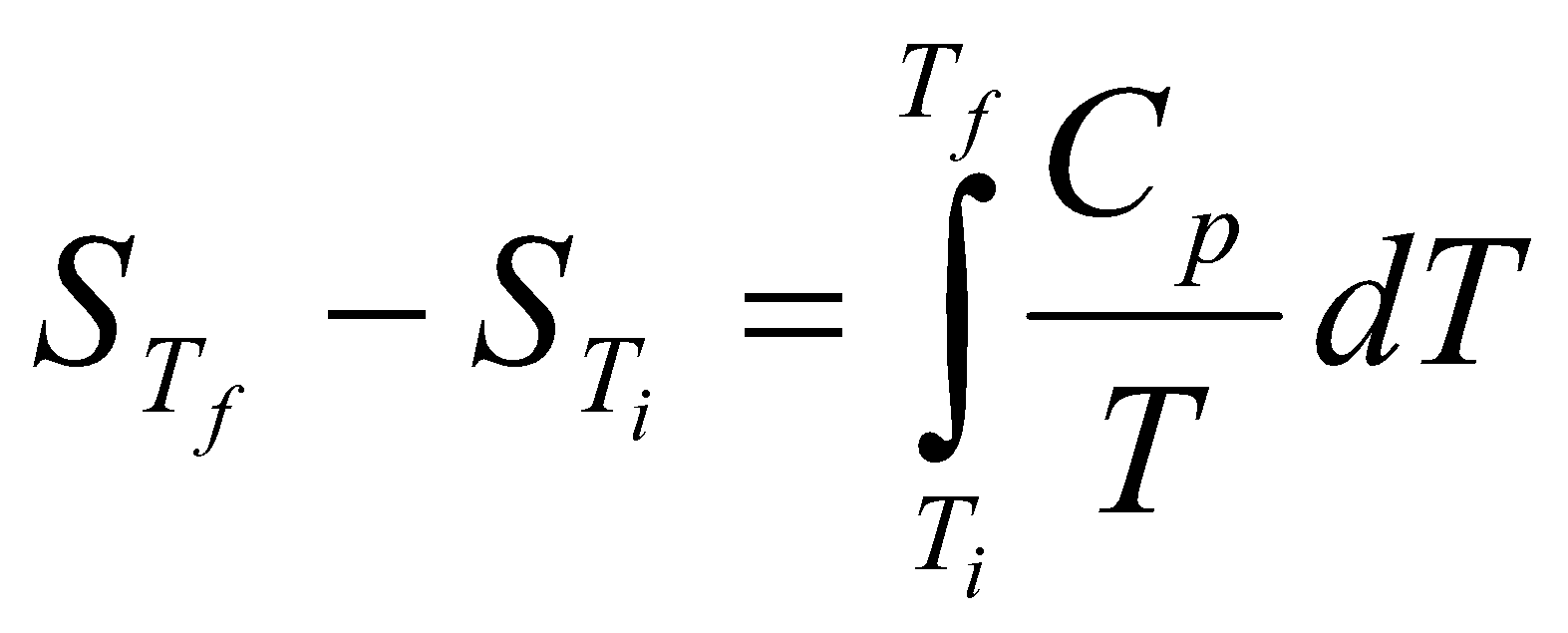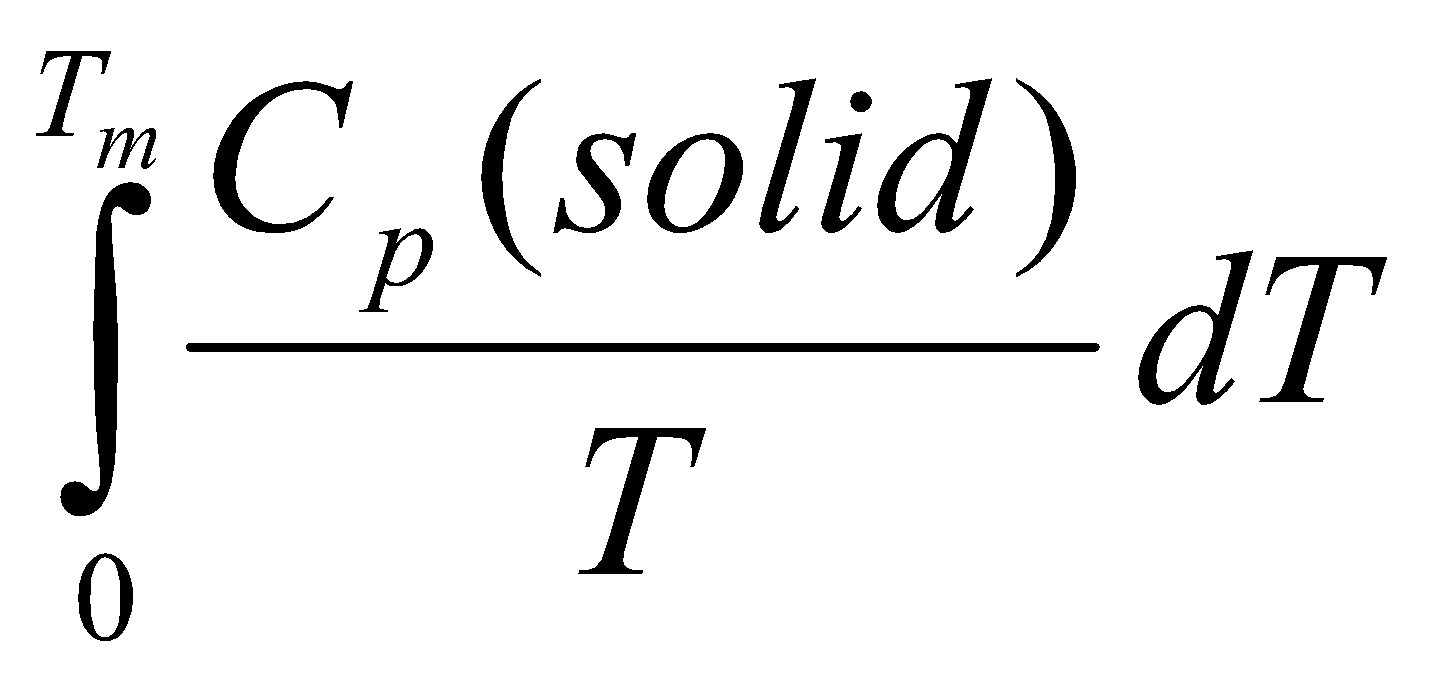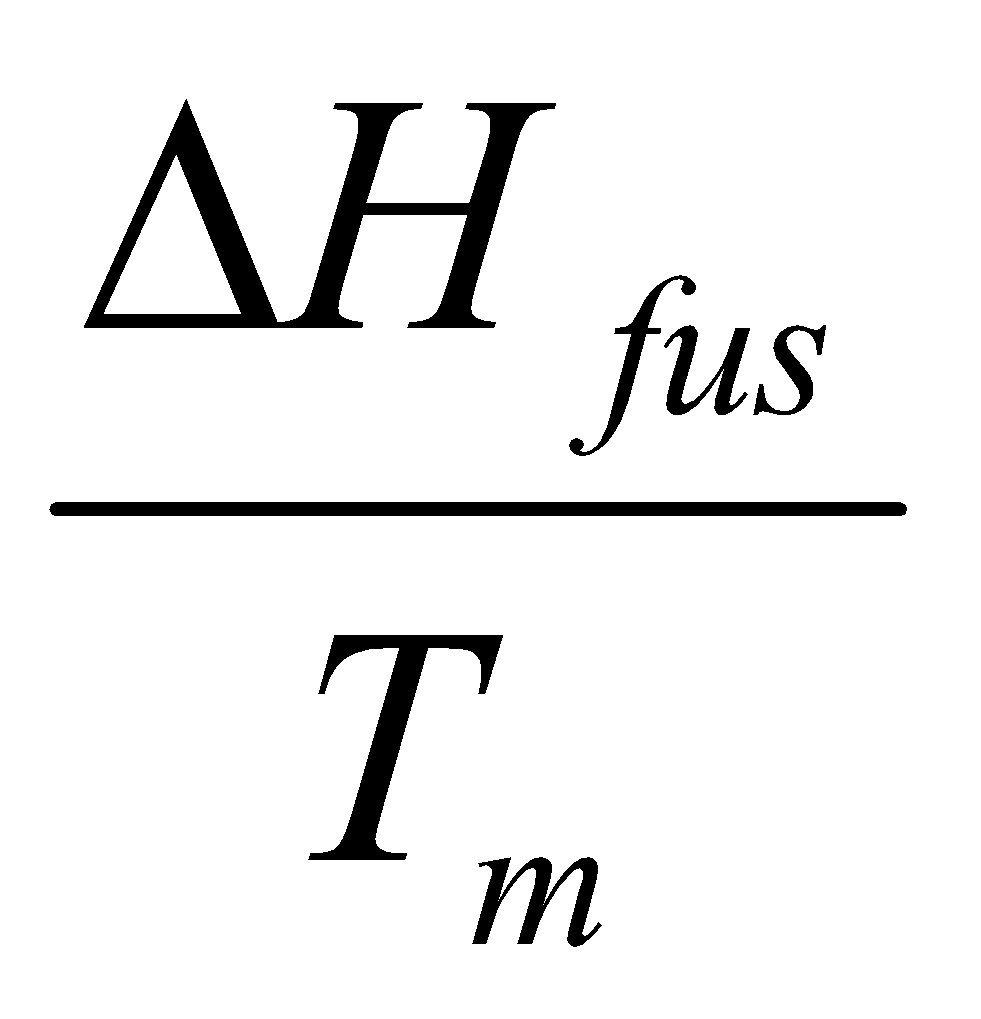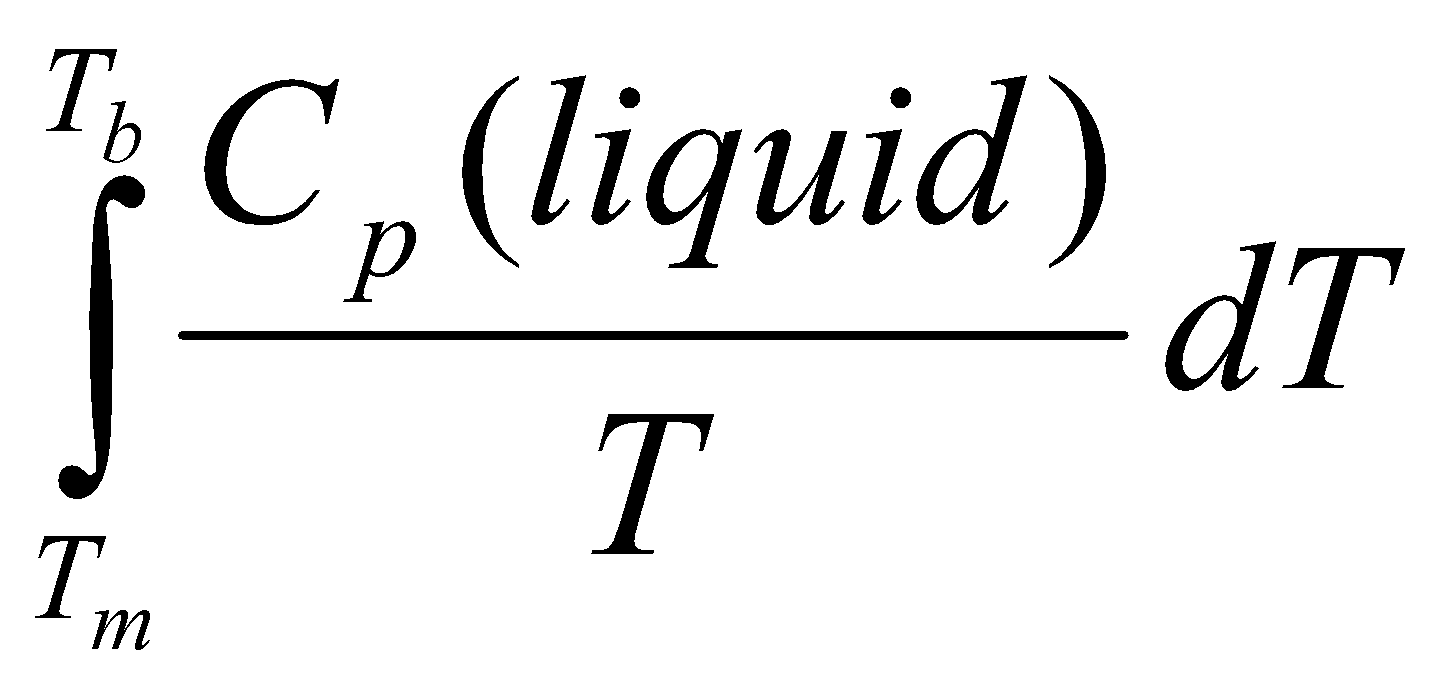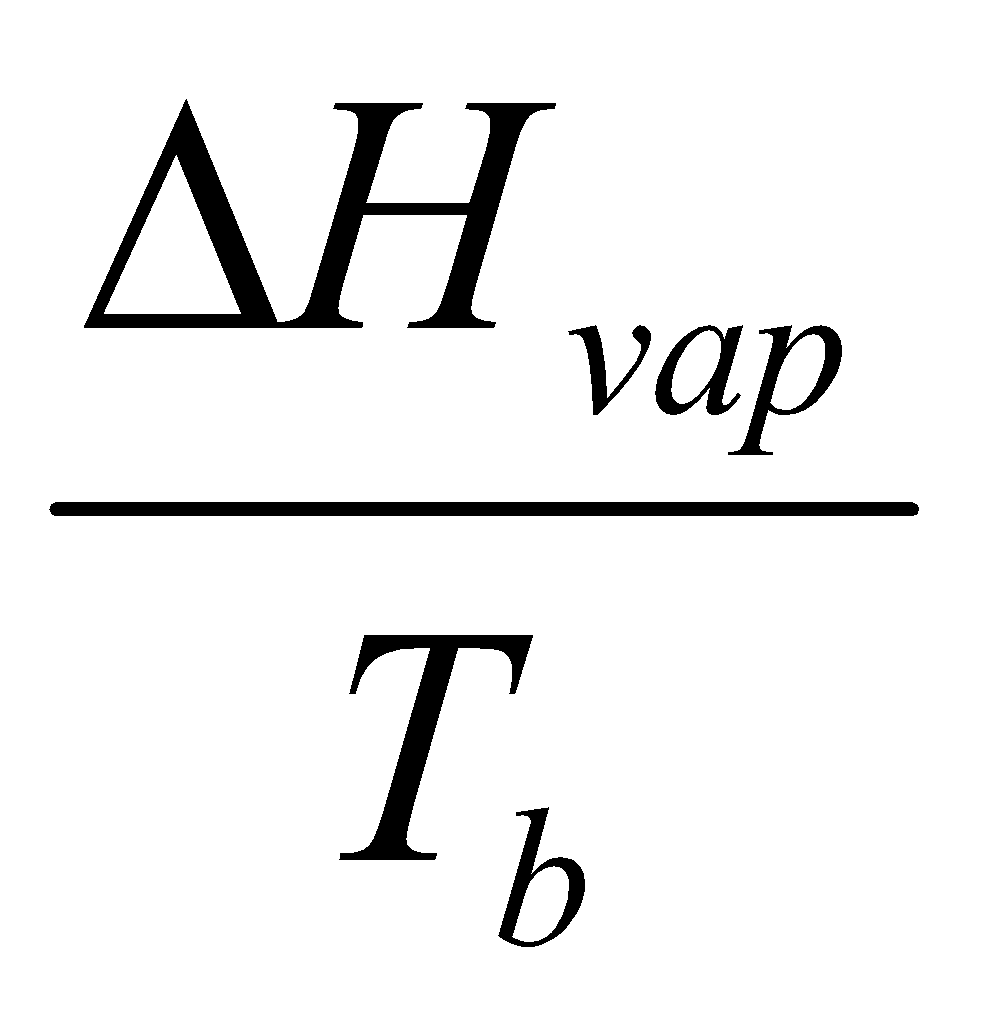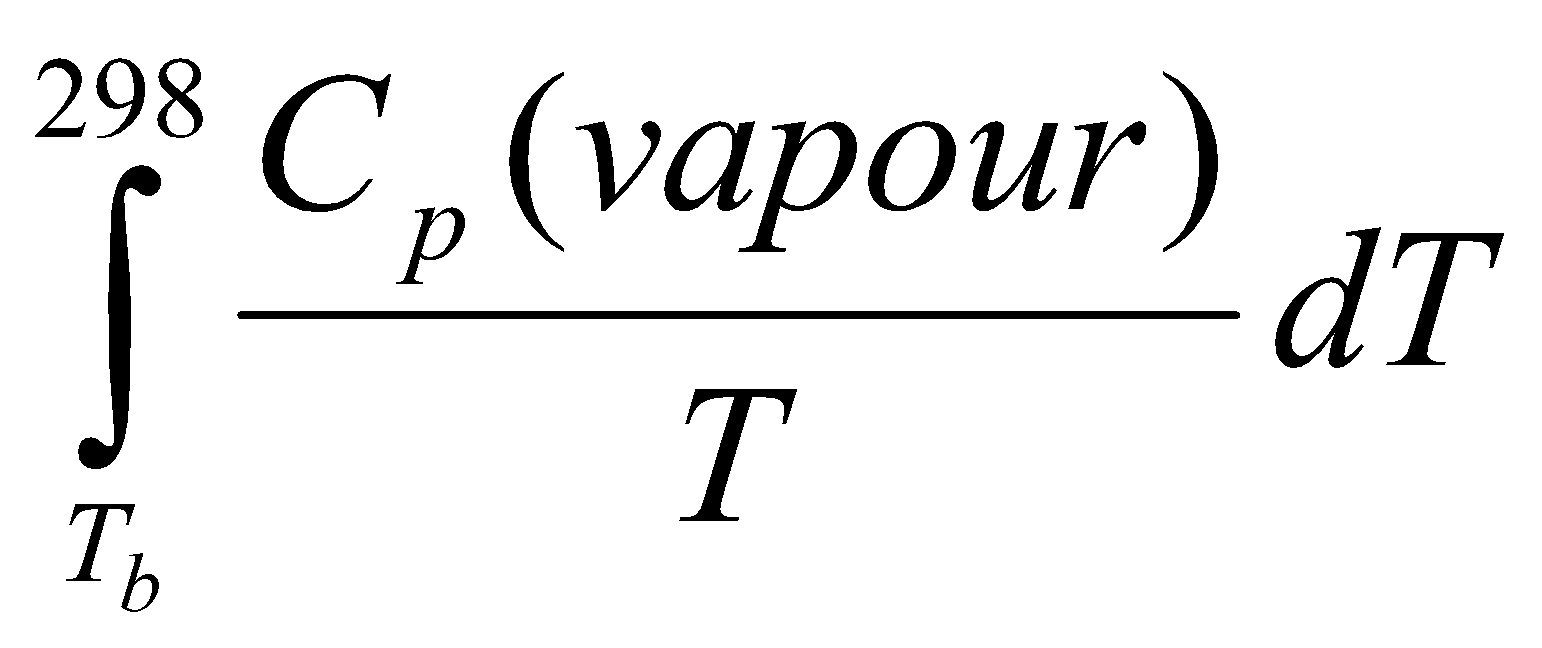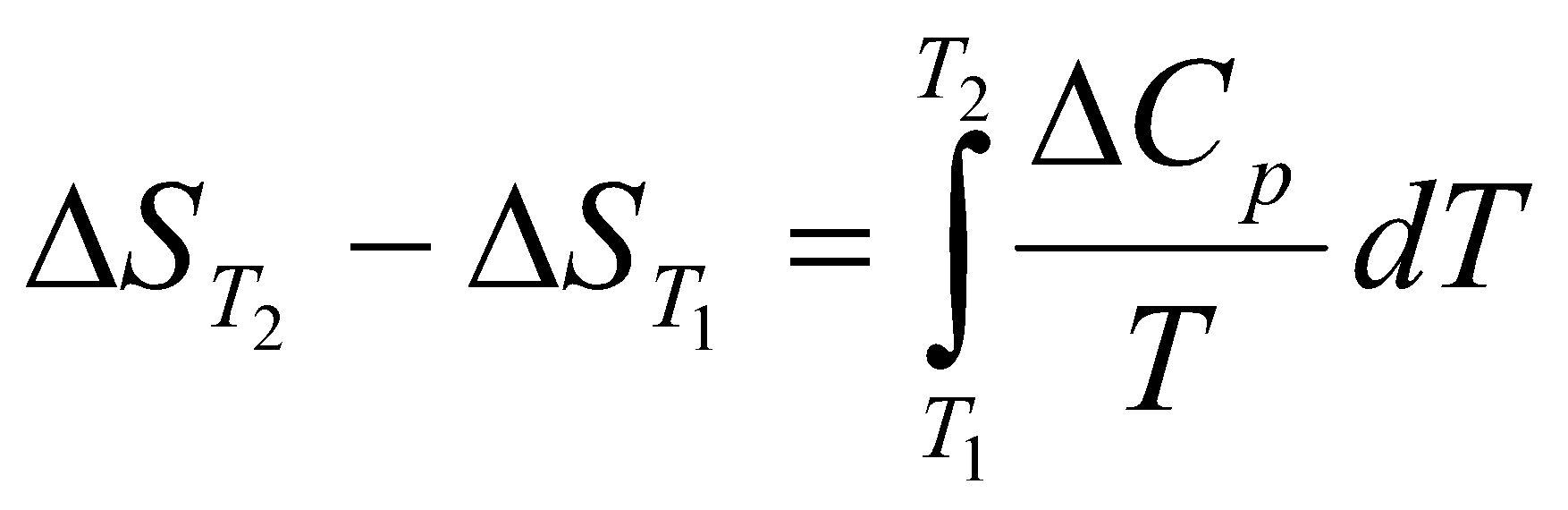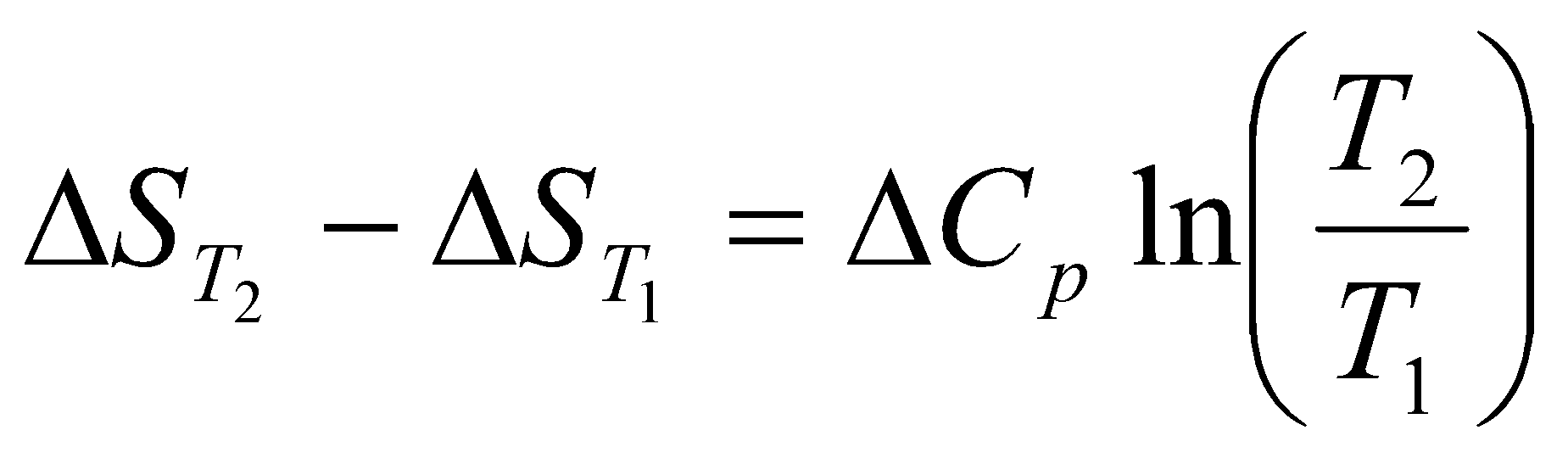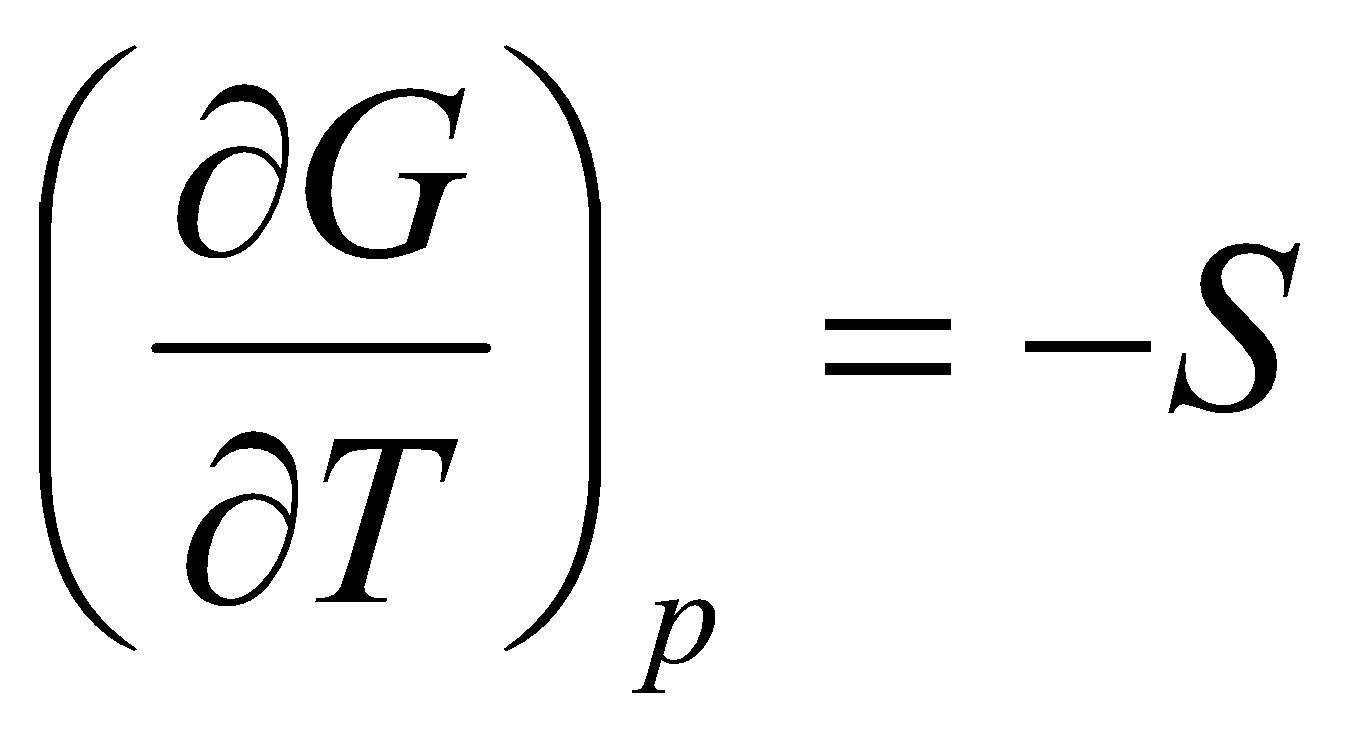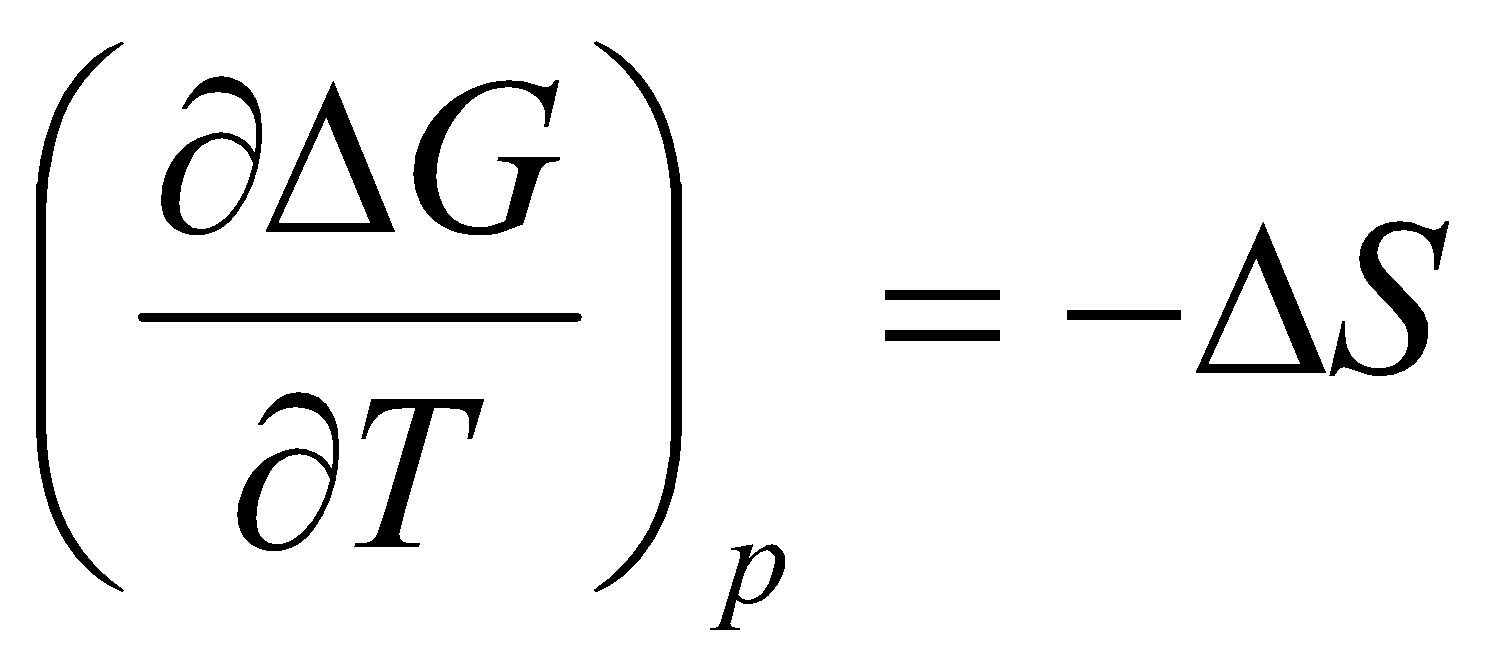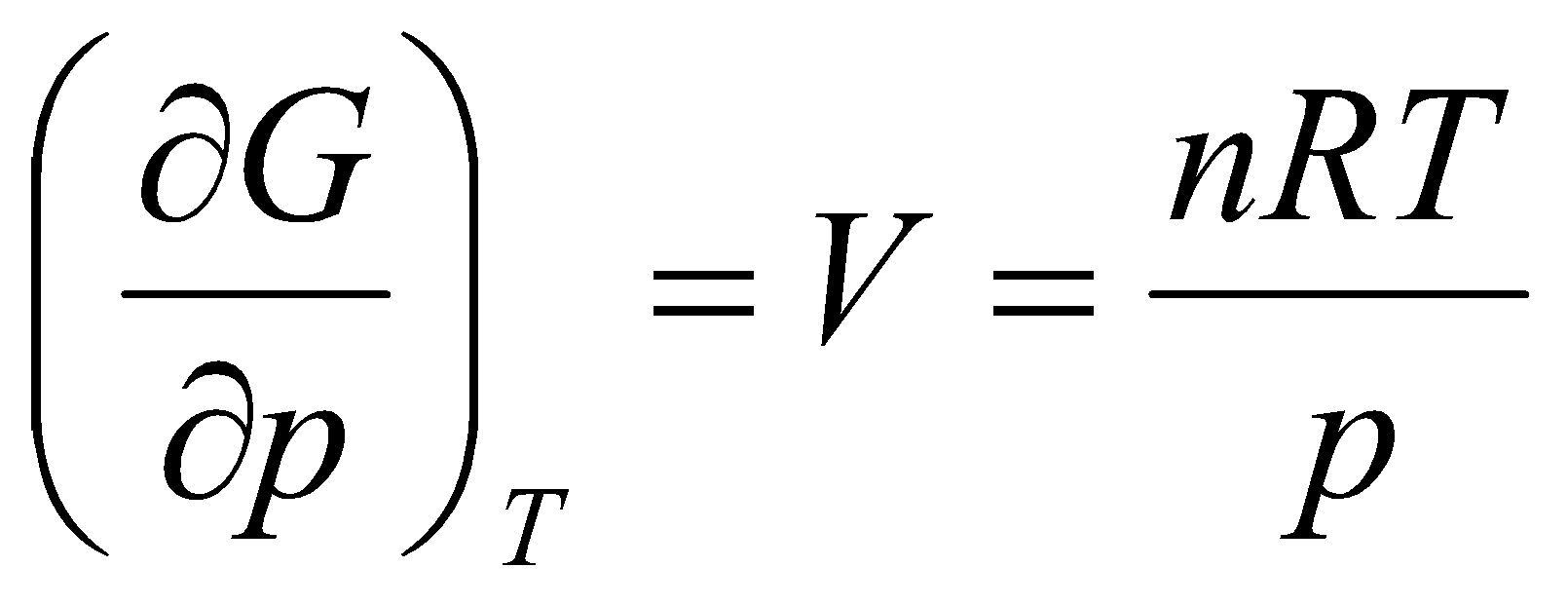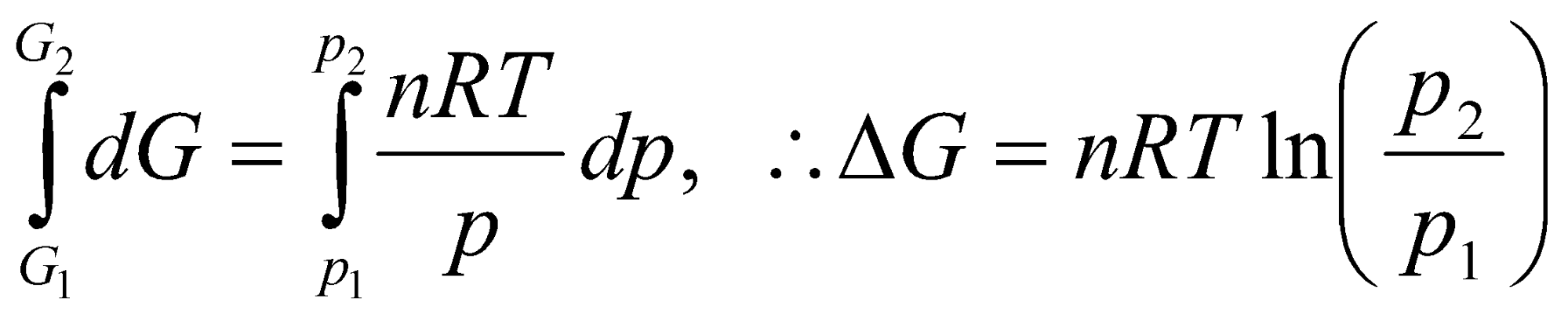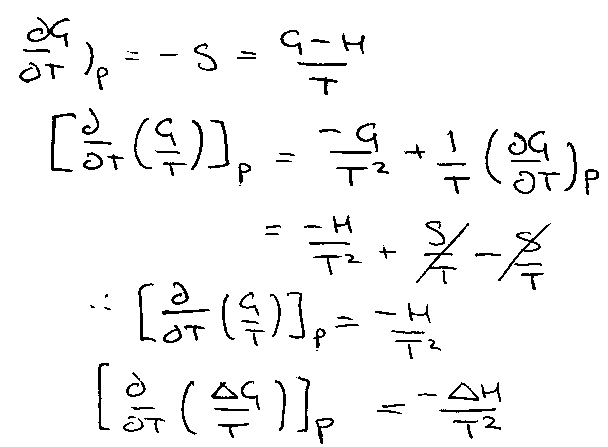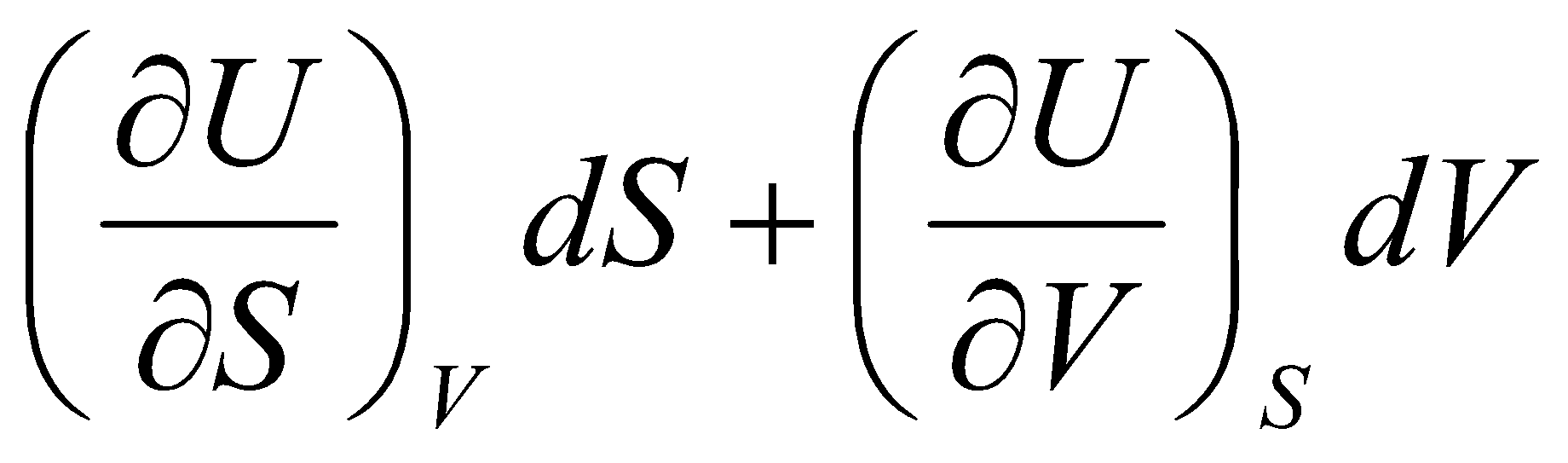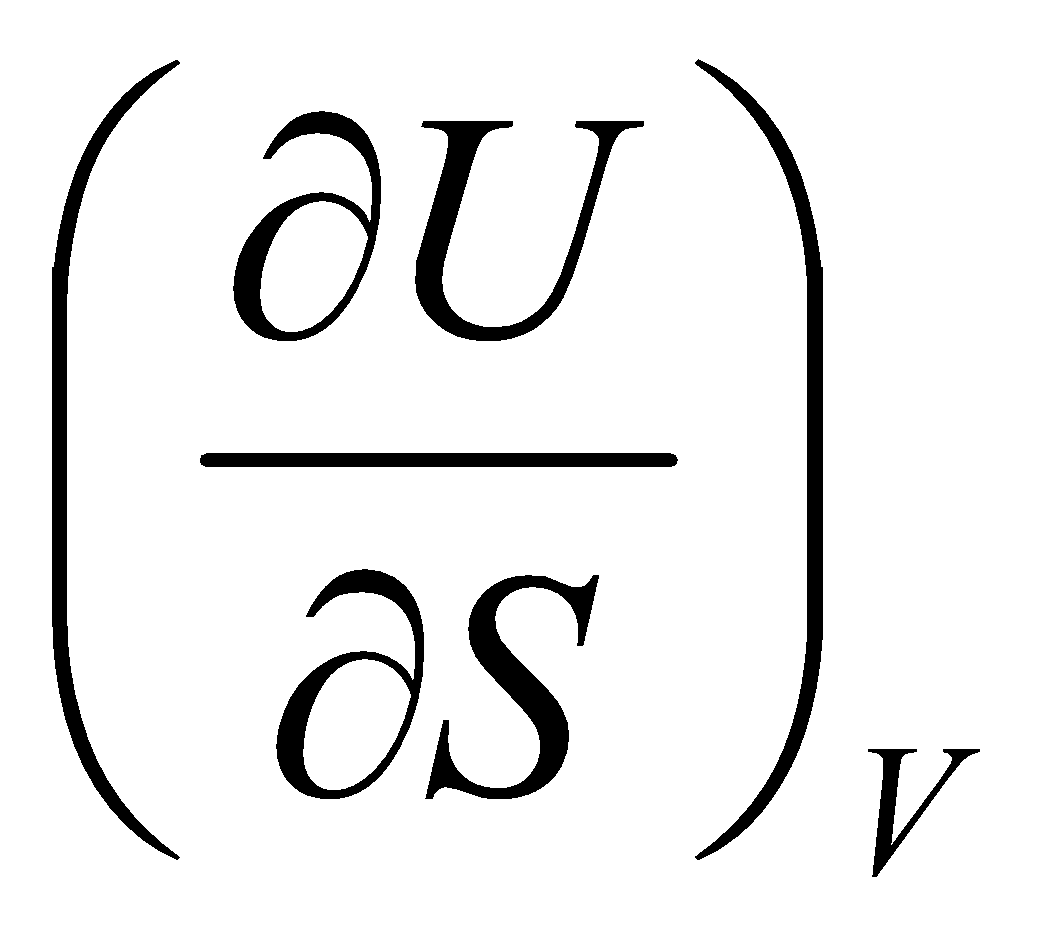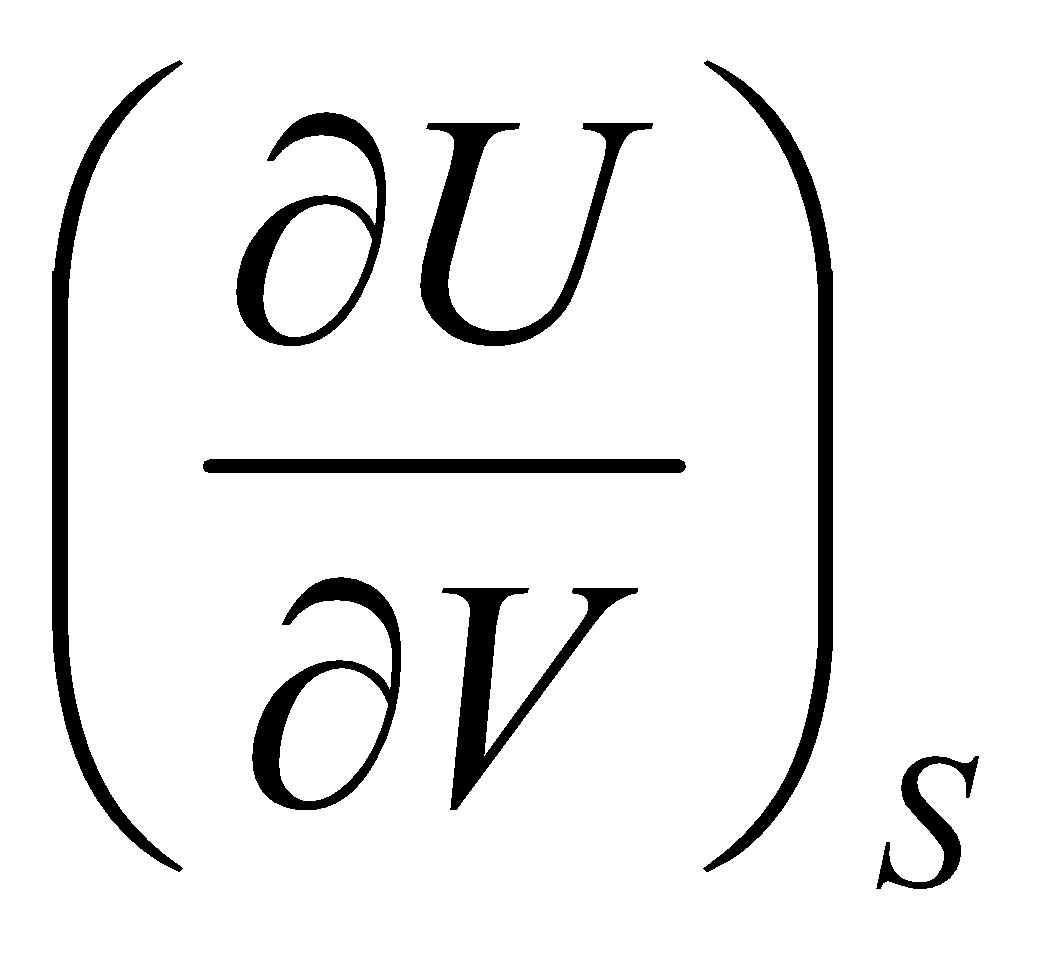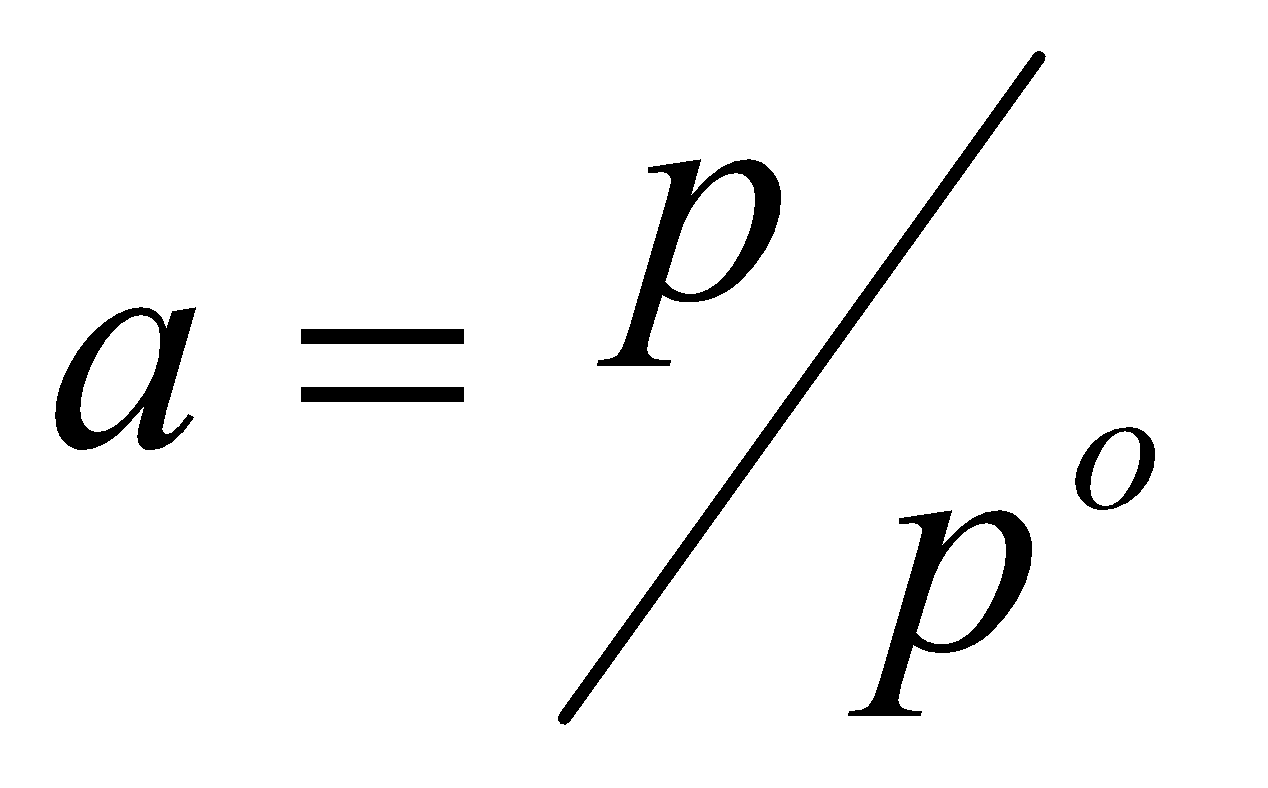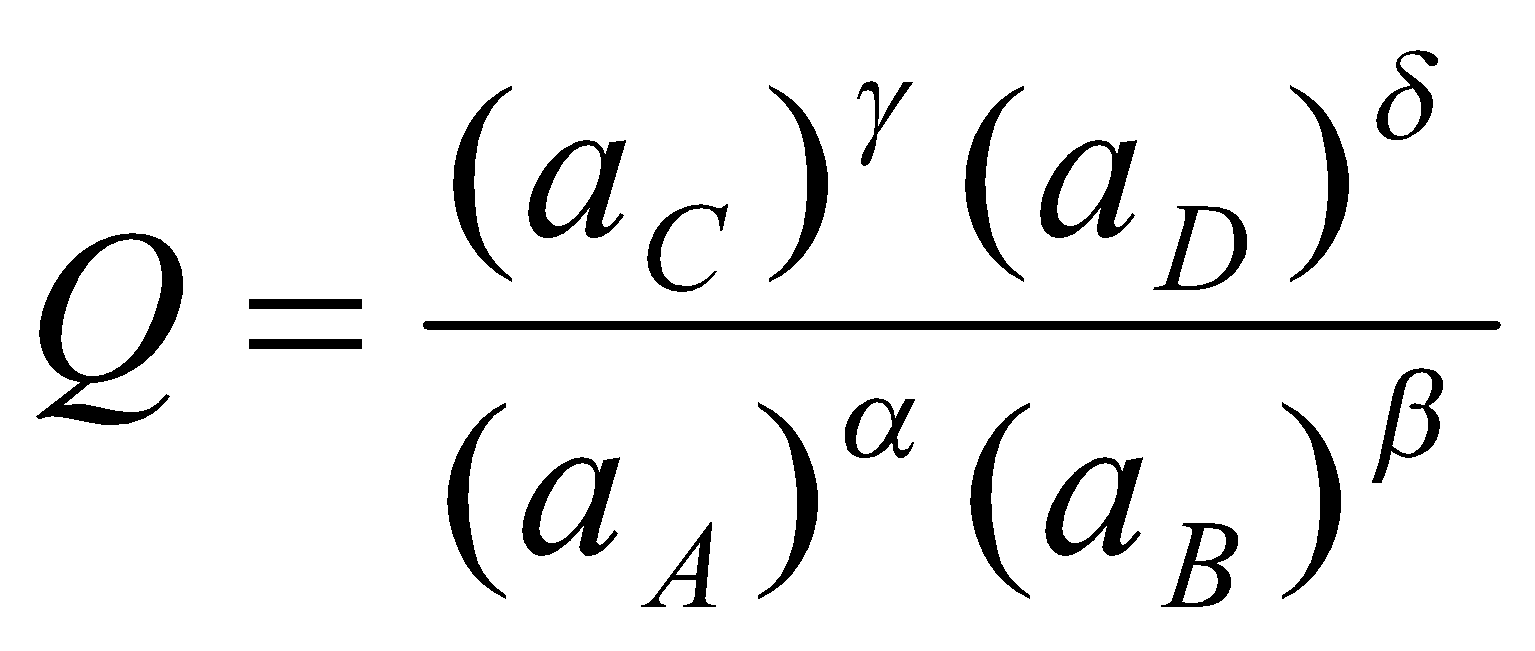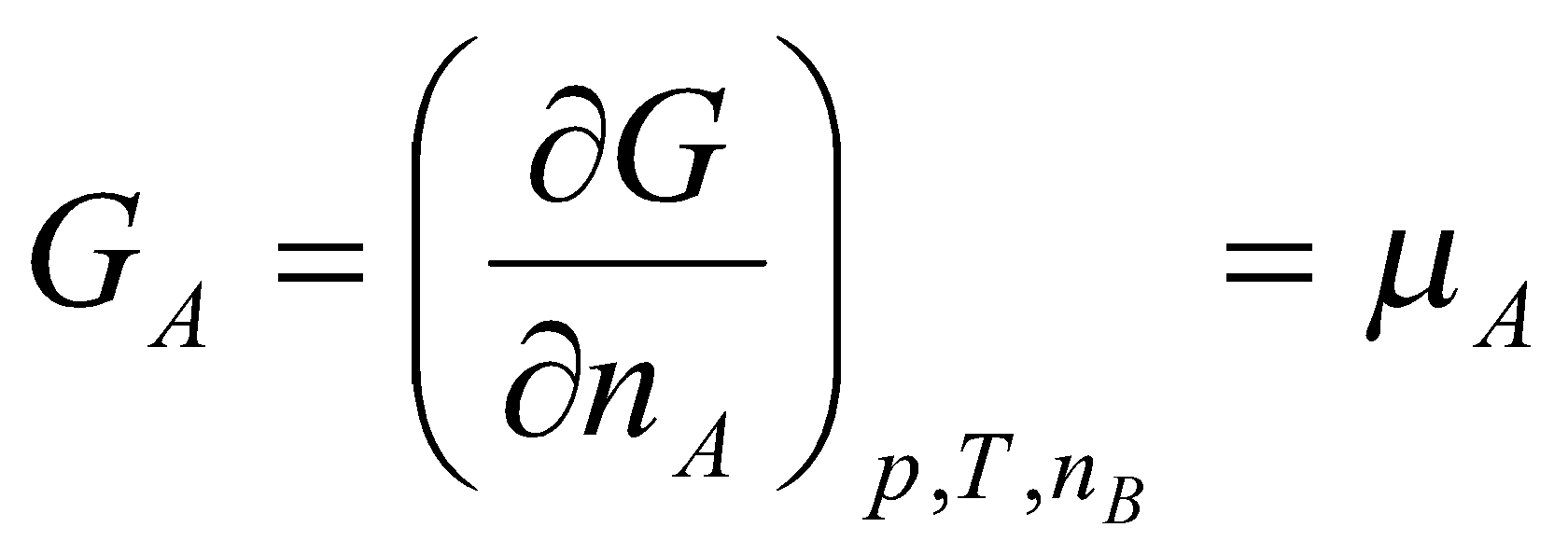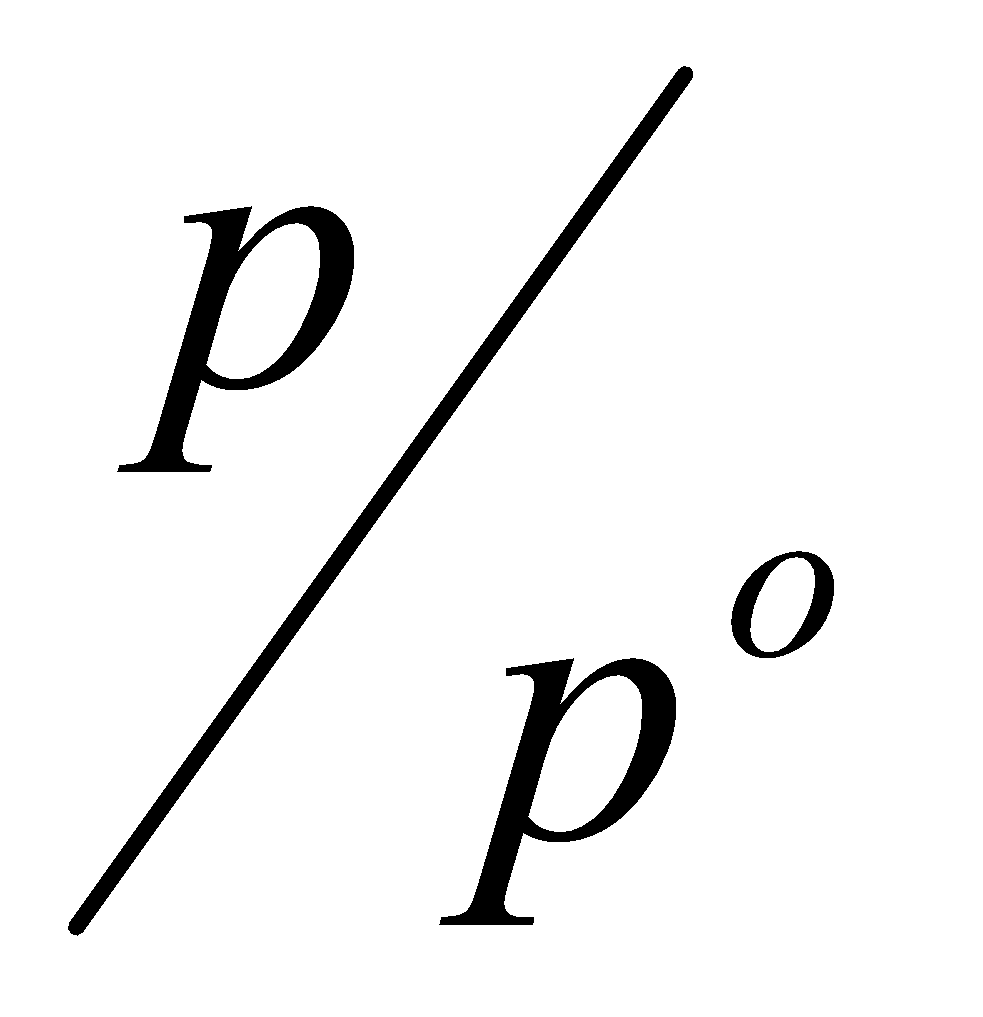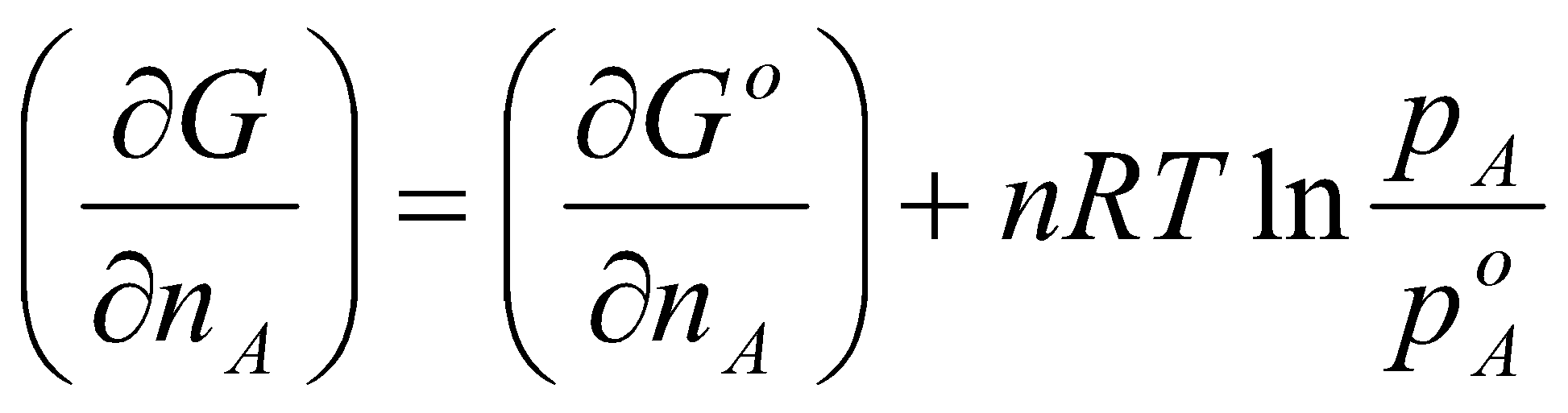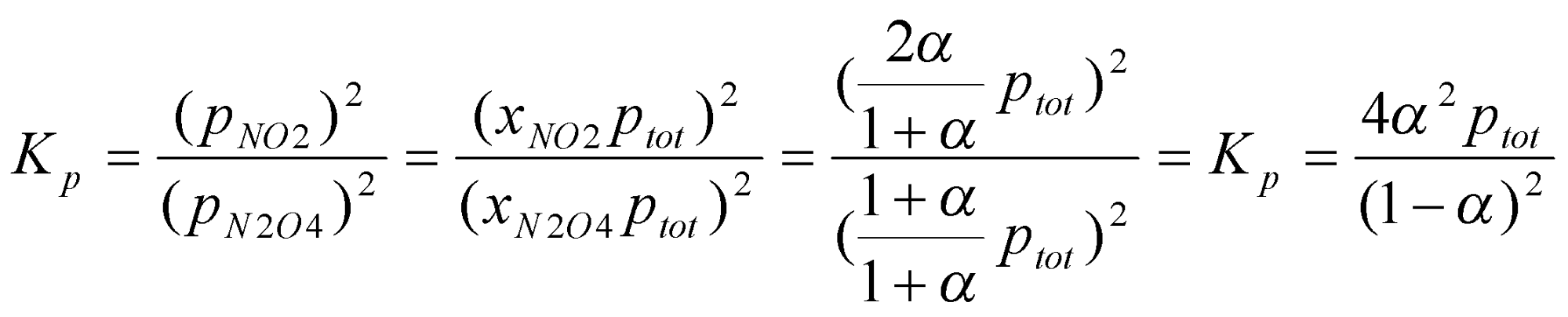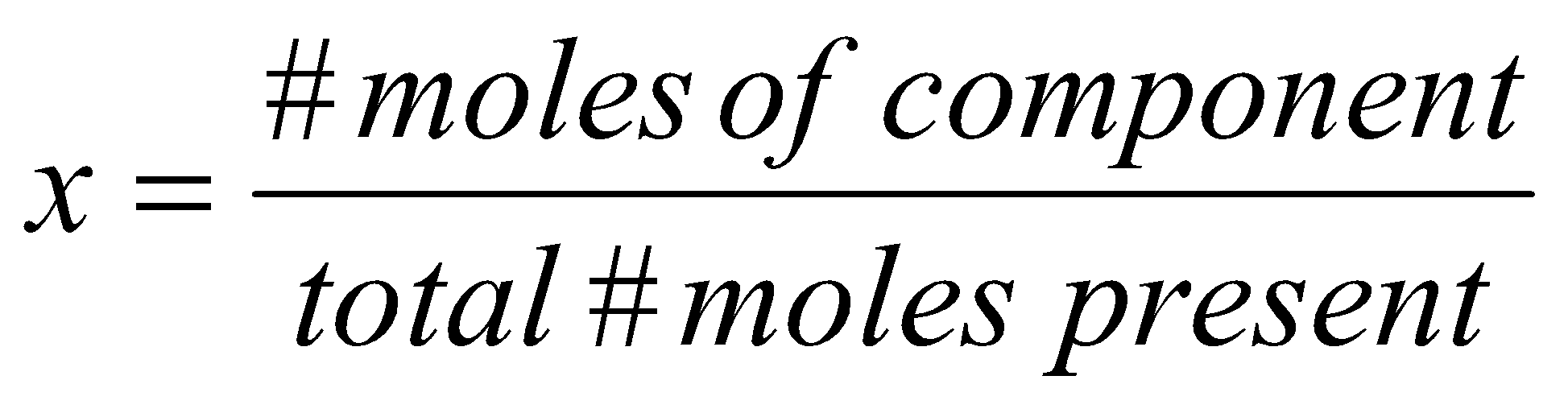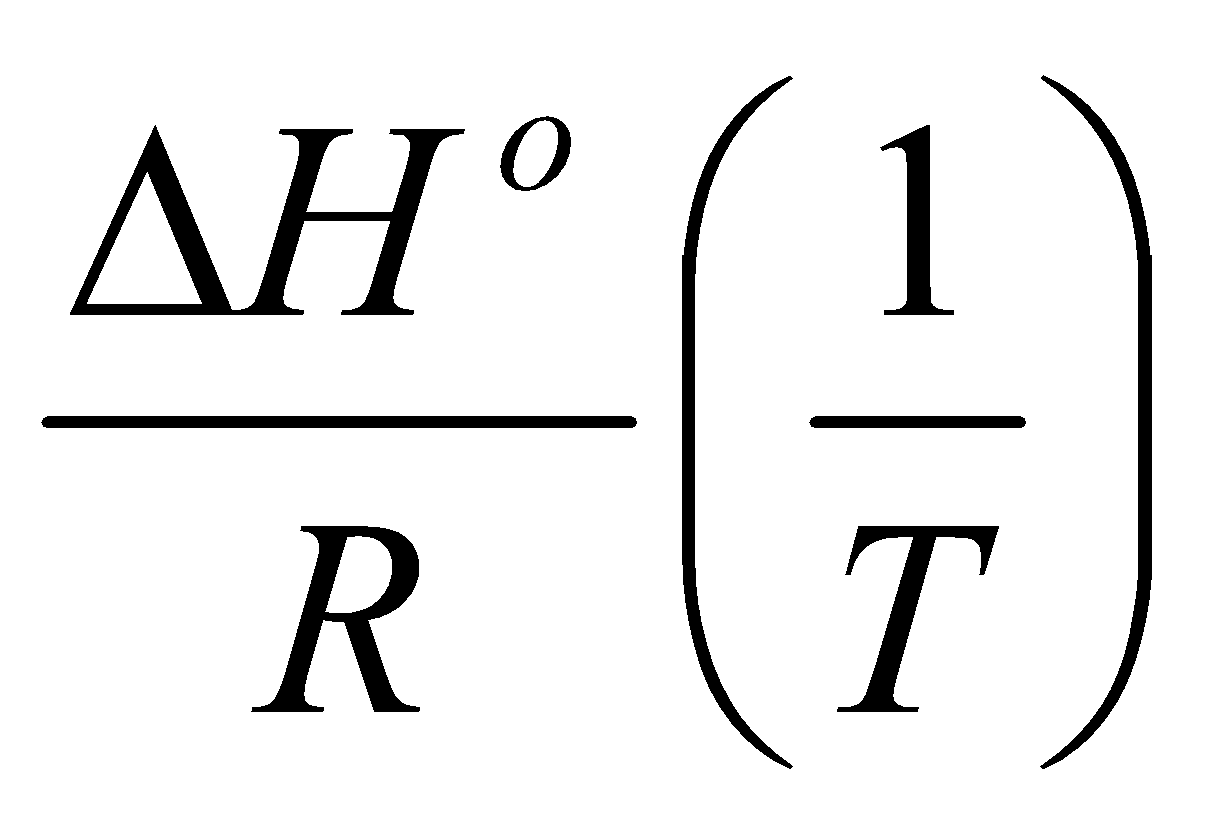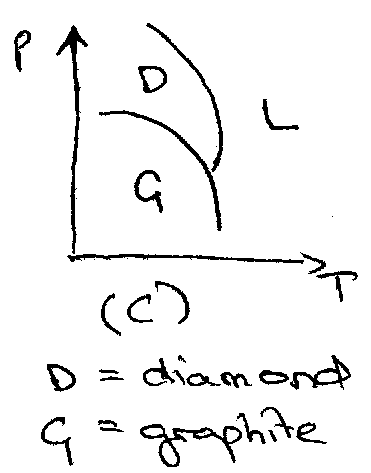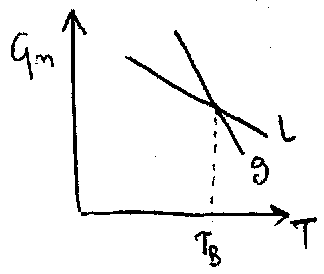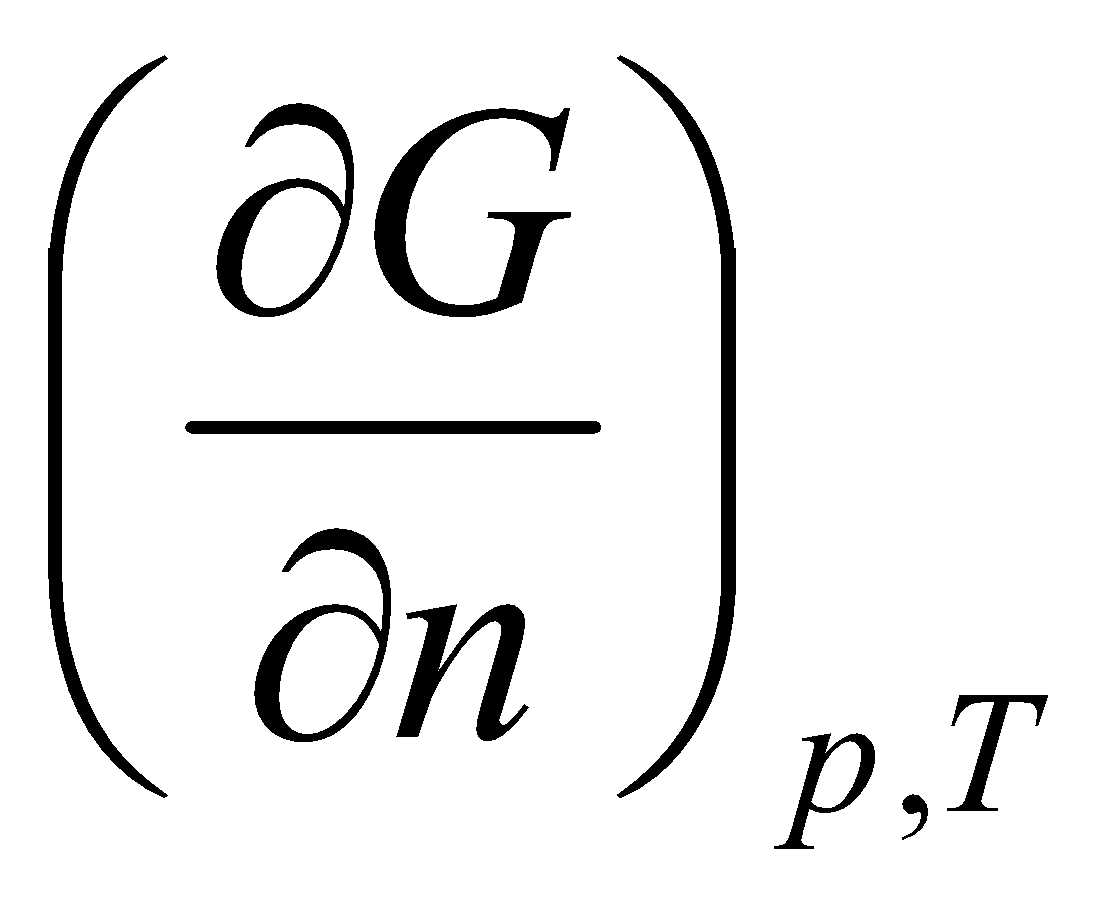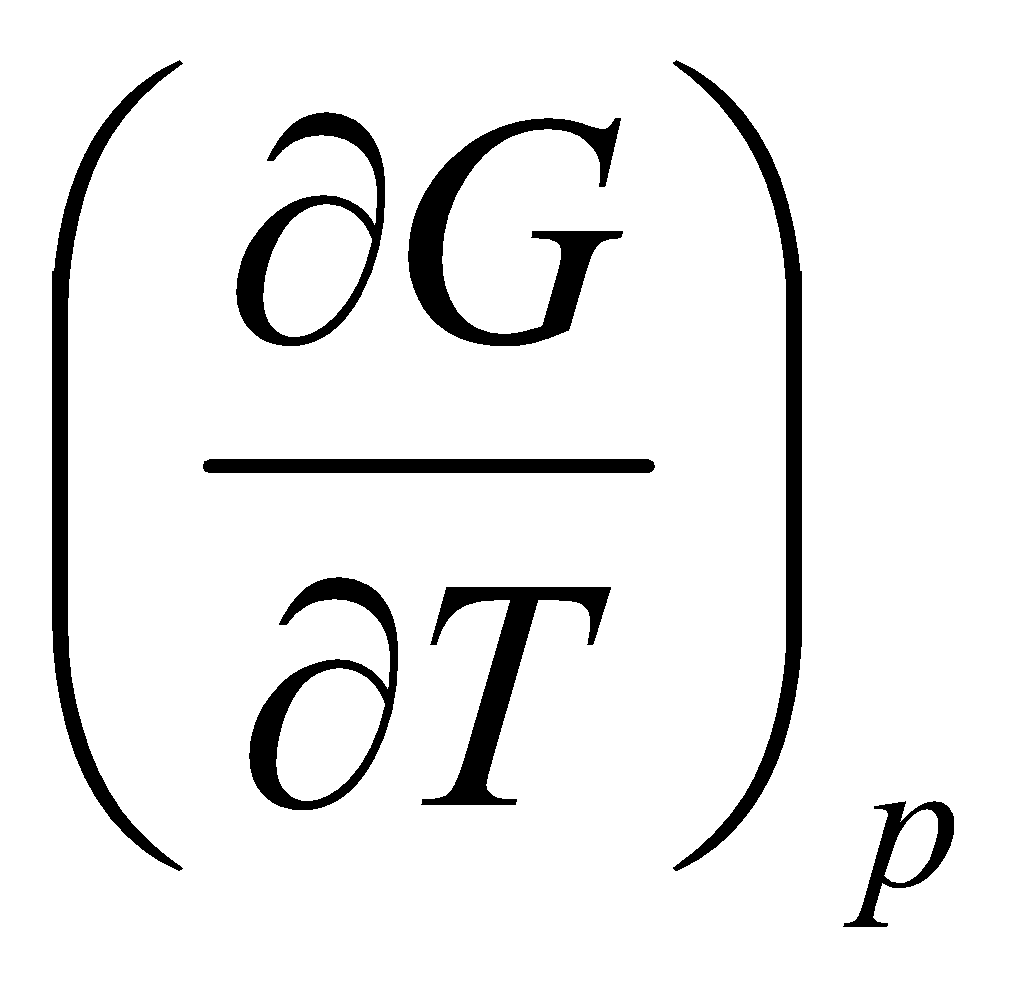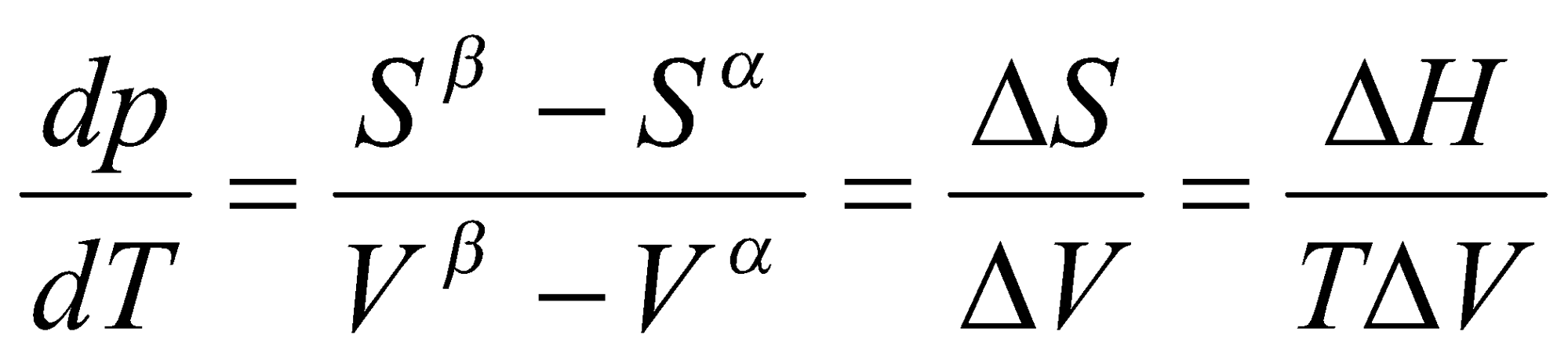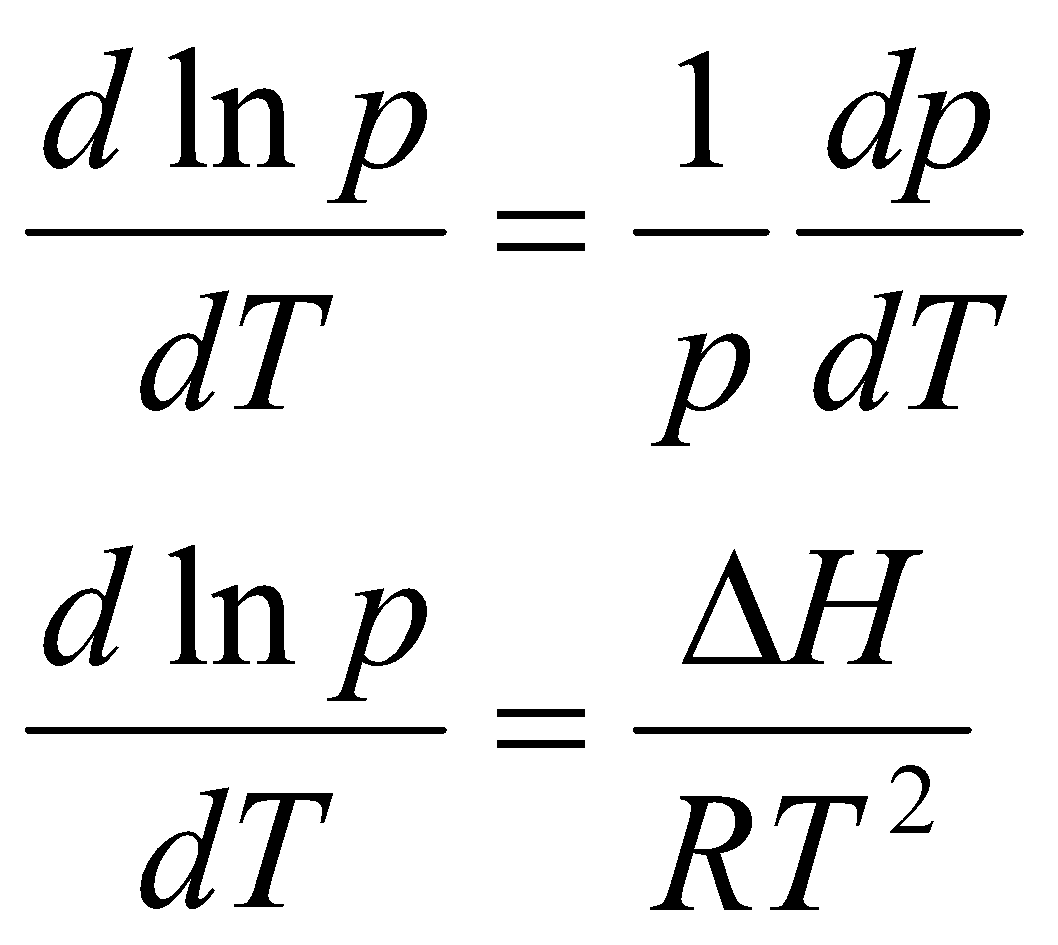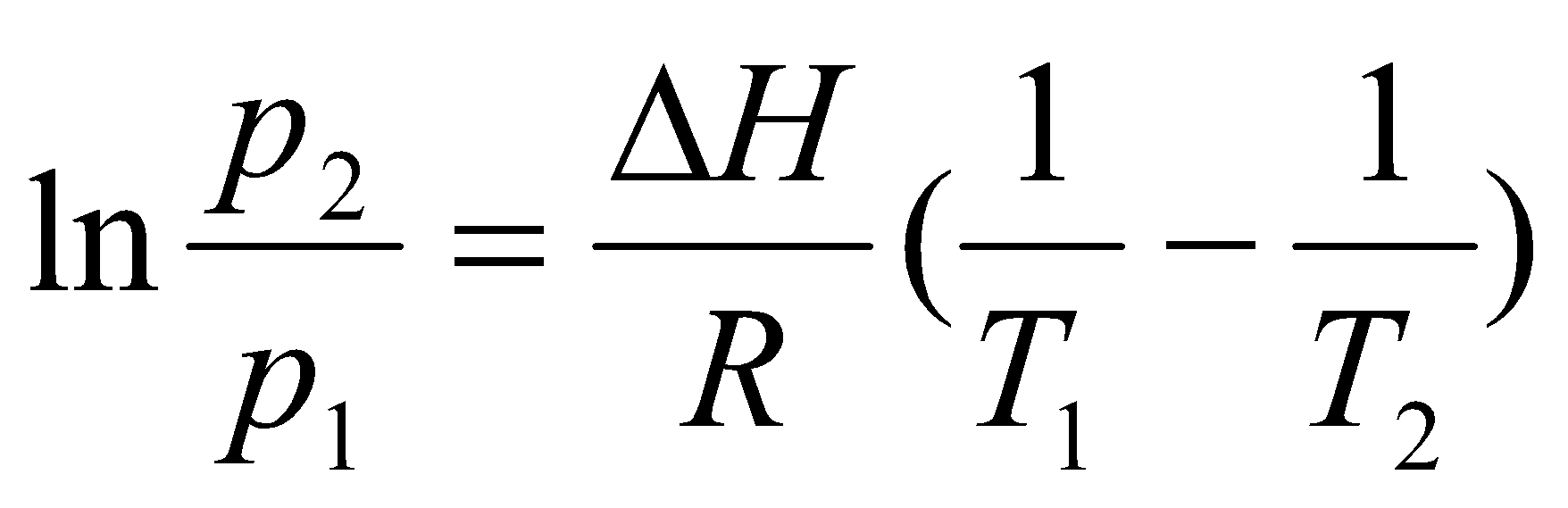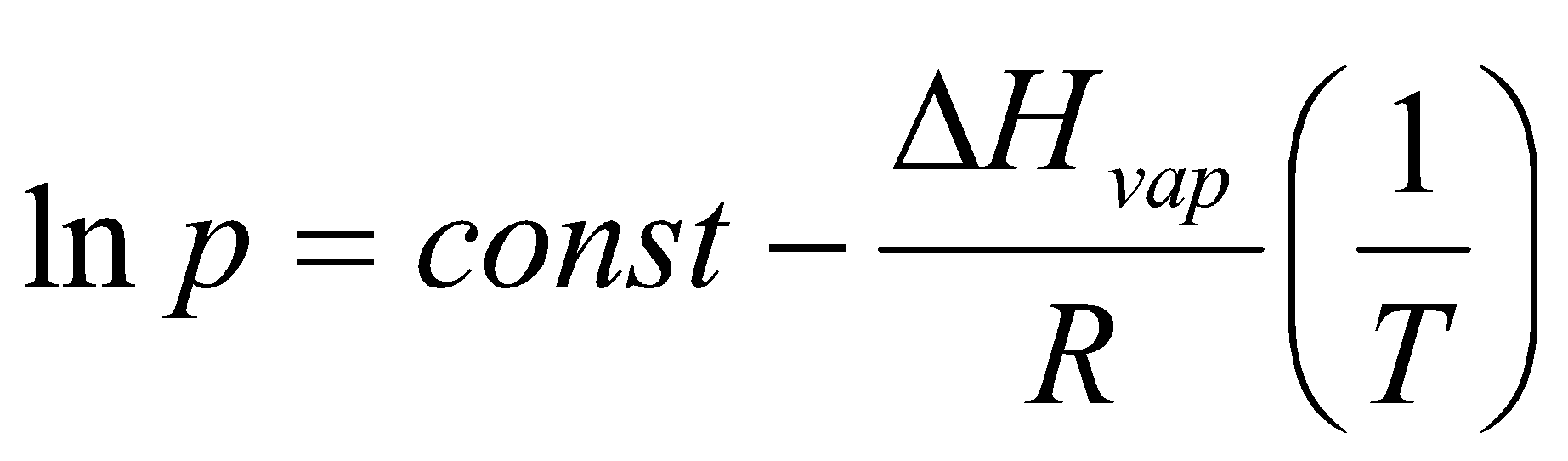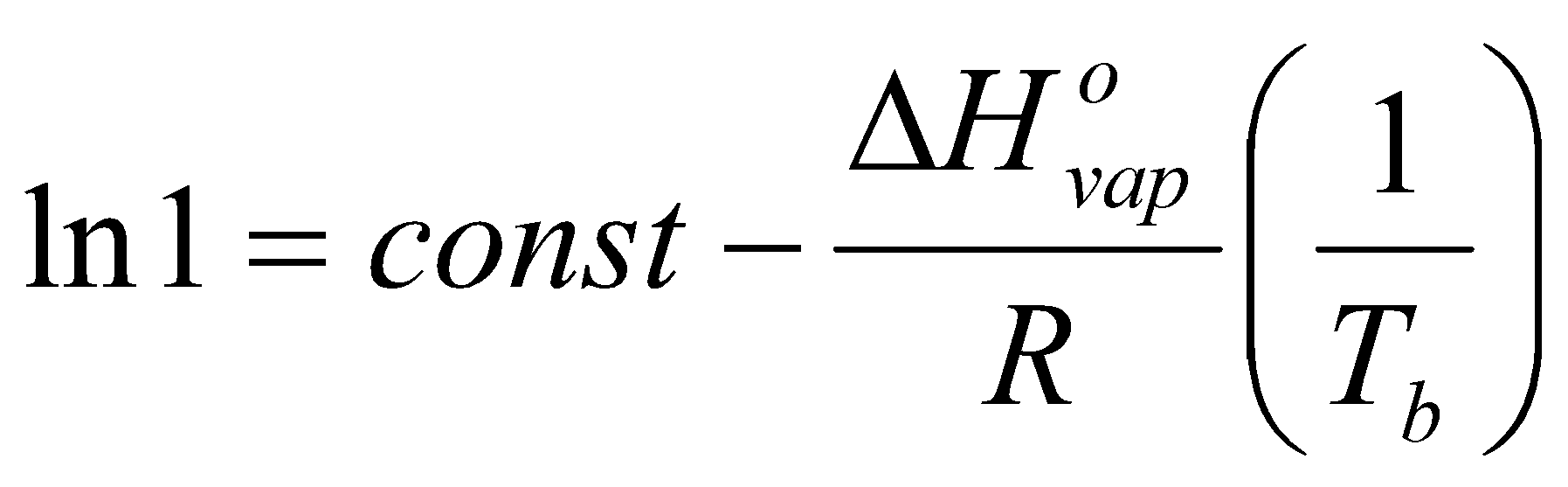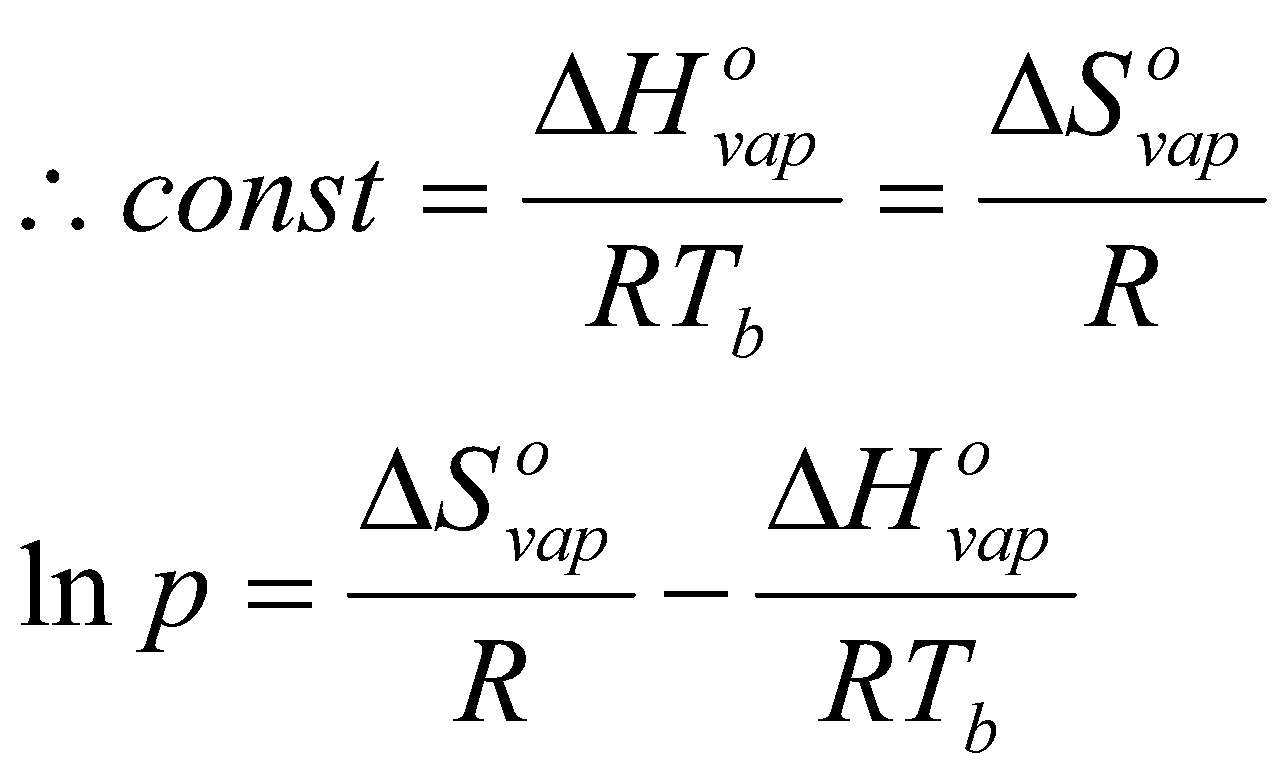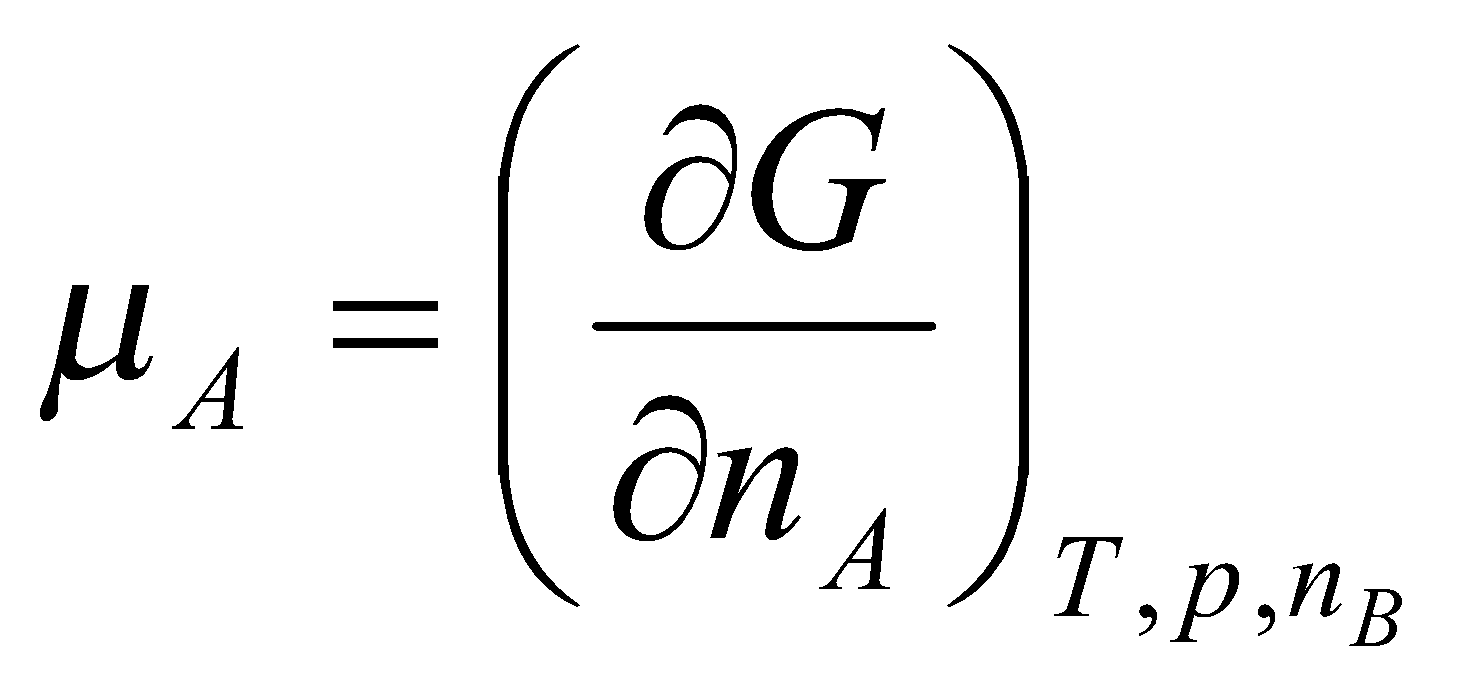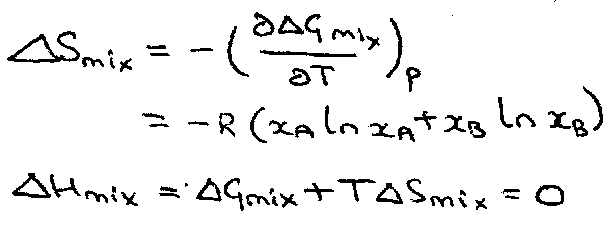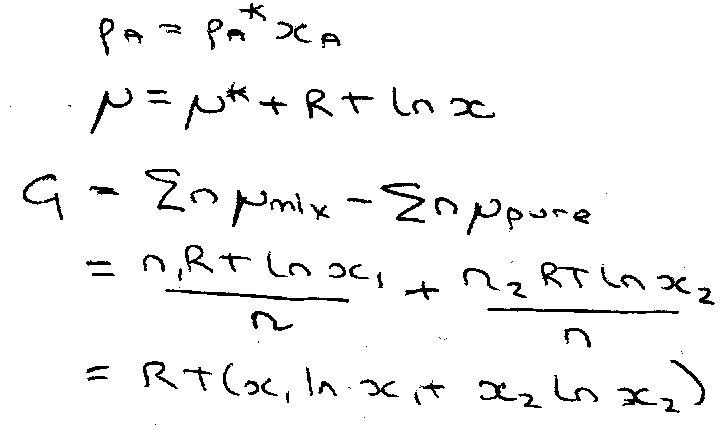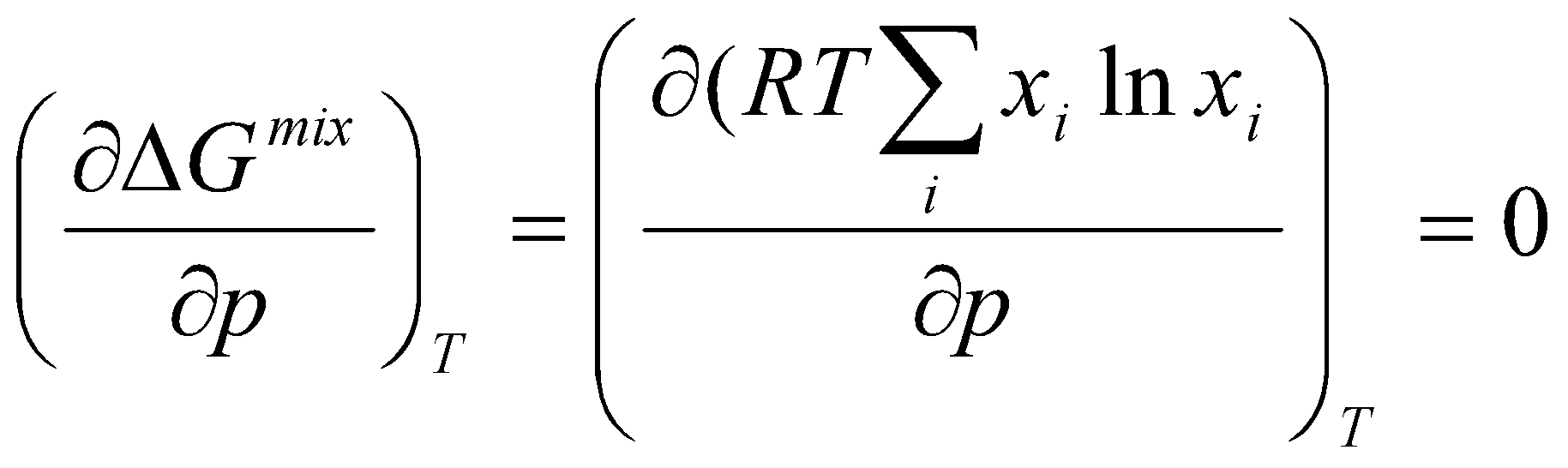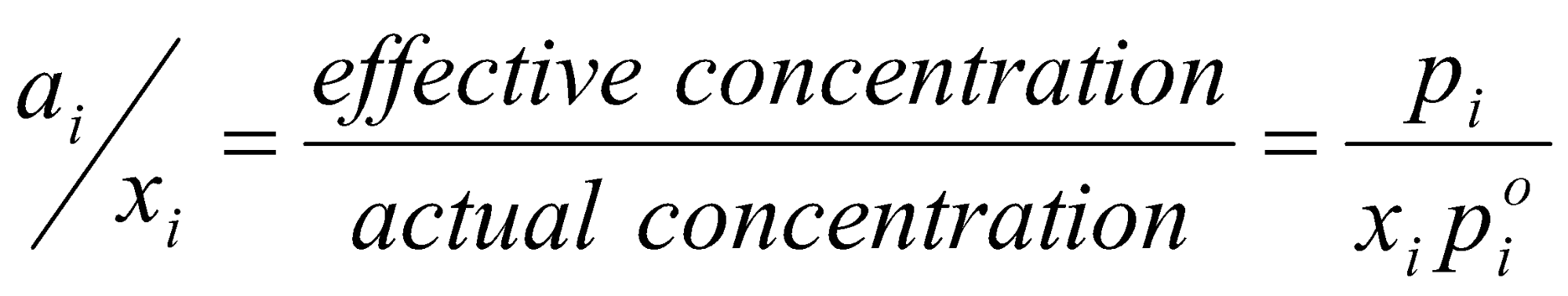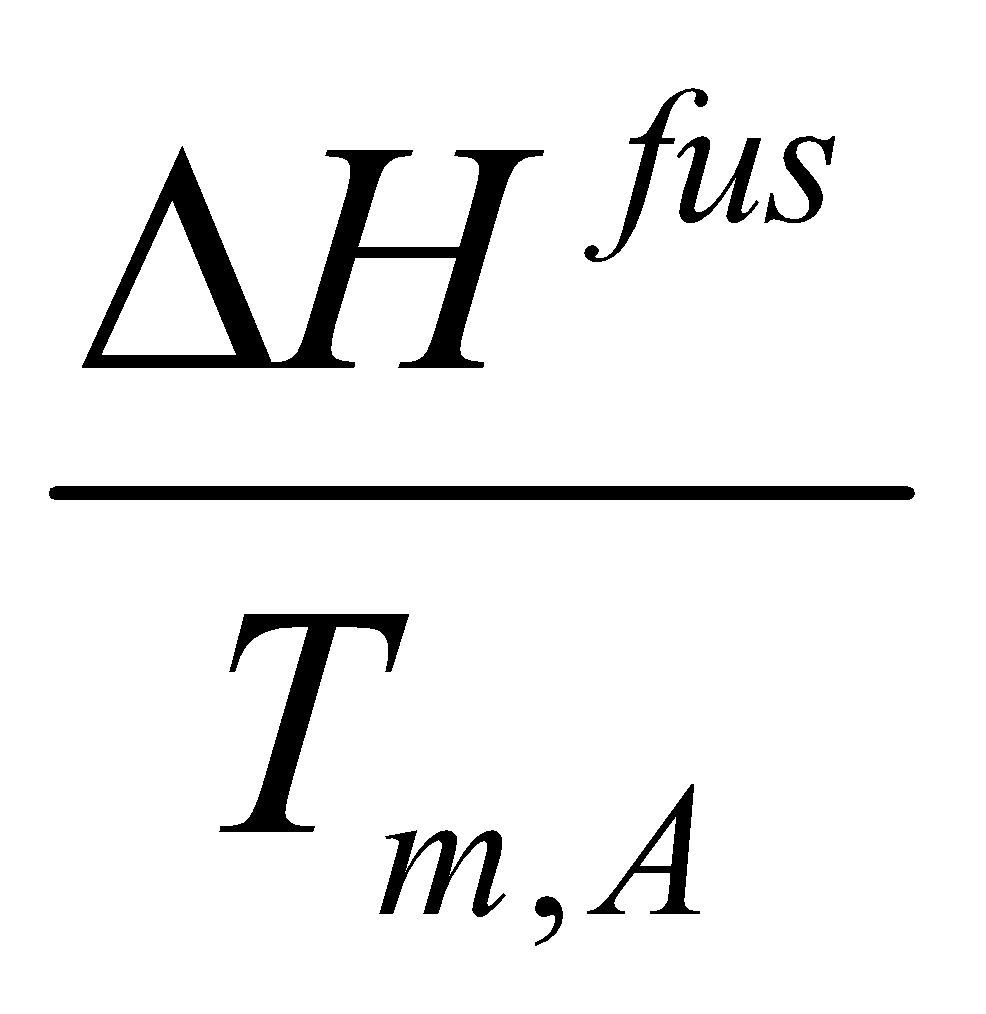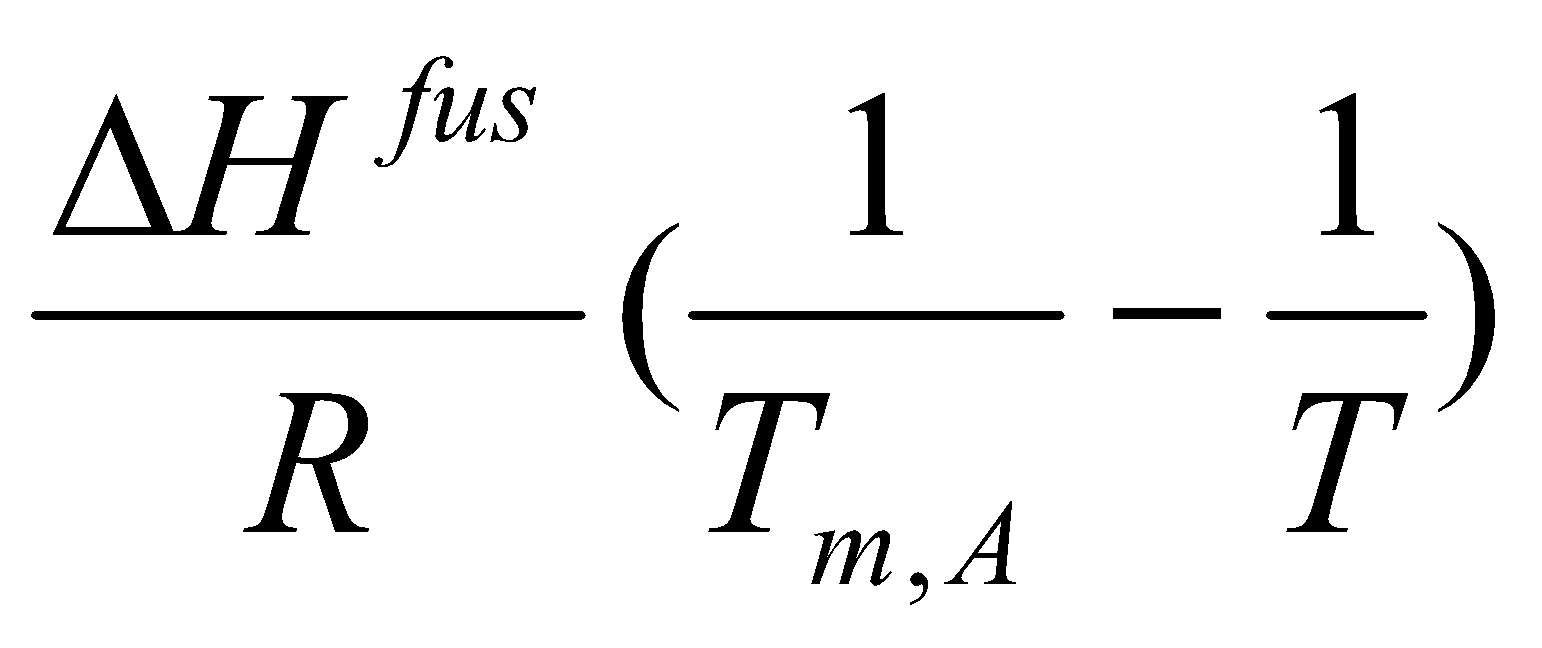Thermodynamics Notes

Energy in Chemical Systems

Perfect Gas –

p =

Realistic Gas –

Van der Waals Equation:

p =

Where a and b are constants, a is for strength of attraction and b is for repulsive interactions. Both are independent of T.

Can be rearranged to give the Virial Equation of State:

p =

Systems

• Open, e.g. test tube. Exchange energy and matter.
• Closed, e.g. bunged test tube. Exchange energy with surroundings only.
• Isolated, e.g. bunged test tube with insulation. Exchanges nothing.

Work and Heat

Work – uniform movement of atoms. Lifting a weight.

Heat – random motion of atoms. Vibration (temperature gradients only). No transfer of heat means adiabatic barrier. Otherwise it is diathermic.

W > 0 when work is done on the system. Energy transferred to the system.

W < 0 when work done by the system, energy lost.

q > 0 when E transferred to the system, and vice versa.

Internal Energy = total energy of all particles. KE + PE.

ΔU = q + W.

For an isolated system, ΔU = 0. This is the First Law of Thermodynamics: that the internal energy of an isolated system is constant.

U is a state function, which means it is independent of the preparation of its state.

• Energy added to or work done on a system = positive.
• Energy removed or work done by a system = negative.

dU is an exact differential. For infinitesimal changes, dU = dq + dW.

ΔU = Uf – Ui, whether the path is adiabatic or non-adiabatic. This is not the case for work and heat.

Work, W = .

Expansion Work –

Taking a piston, where an external pressure is pressing down on an Area so that it is lowered by a distance dz, then dW = -pexA dz, so:

 

dW = -pex dV

So, for Constant external Pressure, W = -pex ΔV.

Free expansion implies pex = 0, so W = 0.

Reversible processes do maximum work. This means an infinitesimal change in conditions. So p → p+dp , or p+dp → p.

Work done by a Perfect Gas:

For a reversible expansion,

W =

Since nRT is constant for Isothermal expansion,

Work = -nRT ( ln Vf / Vi ).

A plot of p against V gives isotherms for each temperature. These approach pex as V increases, and are hyperbolic in shape.

Heat Capacities of Gases

These correlate the amount of energy required for heating a substance.

Amount of energy dqv added to a gas at constant volume causes a temperature change dT, then the constant volume molar heat capacity, Cv is:

dqv = CvdT

Cv =

Enthalpy and Thermochemistry

Describes energy changes at constant pressure. Defined as:

H = U + pV

This comes from ΔH = qp = ΔU + p ΔV, from the 1st Law.

ΔH ≈ ΔU for liquid / solid systems (ΔV is approximately constant).

Evolving heat → exothermic (negative ΔH).

Absorbing heat → endothermic (positive ΔH).

Hess’ Law –

Total ΔH for the reaction is independent of the path of the reaction (true as ΔH is made up of State Functions).

Enthalpy is a state function, and therefore summable (Hess Cycles). Must be at constant T.

Hence, ΔH1 = -ΔH2 + ΔH3.

For infinitesimal changes in H:

dH = dU + Vdp + pdV

Hence,

dH = dq + Vdp

From this we see that dH = dq (at constant p).

Also, Hm = Um + pVm                                 (where subscript m indicates molar).

For a perfect gas, Hm = Um + RT                (RT is constant, 2.5kJ mol-1).

Heat Capacity 

Cp =

Cp is the amount of energy needed to raise the temperature of 1 mol of substance by 1K at constant pressure.

Cp > Cv (Gradient of q against T is higher for H than U).

Cv =                                 Cp =

The standard state of a substance is the pure substance at 1 bar.

Using the above and Hess’ Law, we can obtain:

Hm(T2) = Hm(T1) +                         [ Kirchoff’s Law ]

Thus,

ΔrH  ΔrH + (T2-T1) ΔrCp

Similarly,

ΔrCp = Σ(prod) nCp,m – Σ(react) nCp,m

Enthalpies of Reaction –

Consider R → P.

Enthalpy at 25oC → ΔHof, 298 (R)

Enthalpy at some other temperature, T: [ΔHof, 298 (R) + Cp(R)(T - 298)]

The same is true for P.

ΔHoT (reaction) = ΔHof, T (P) - ΔHof, T (R) → ΔHoT (reaction) = ΔHo298 (reaction) + ΔCp(T - 298)

ΔCp is the change in mean Cp between P and R.

So far have assumed that the use of mean heat capacities gives sufficient accuracy. In fact, Cp can change significantly.

Use,

Cp (T) = a + bT + cT2 + dT3 + …

Hence,

HT2 – HT1 = [a(T2-T1) + b/2(T22-T12) + c/3(T23-T13)]

Standard Enthalpy of formation is the standard reaction enthalpy for formation of the substance from its elements in their reference (most stable) states.

Entropy in Chemistry

Spontaneous – occurs without work needing to be done.

2nd Law – spontaneous processes are those which cause an increase in the entropy of the universe.

Tendency for matter to disperse – diffusion.

Tendency for energy to disperse – conduction.

Internal Energy is the quantity of Energy.

Entropy is the quality of Energy.

A spontaneous process in an isolated system gives rise to an increase in Entropy (Clausius Inequality).

dqrev is inexact, so an integrating factor 1/T is required.

dS is exact, and so S is a State Function.

Qualitative proof –

more heat → more disorder, so dSdq.

A higher temperature means the disorder is affected less by a given increase in heat, so dS 1/T

Isothermal Reversible Expansion of a Perfect Gas:

dq = dU – dW, and dU/dV)T = 0.                                dq = -dW

dW = -pdV                                                p = nRT/V

Thus,

ΔS = nR ln

Change in Entropy when a system is heated:

dS = =Cp

Cp usually depends on Temperature. However, when it is constant (for a given temperature range),

ΔS = Cp ln

Often the best way to find the change in entropy is by graphical means – the area under the graph of Cp/T against T between Tf and Ti.

Absolute Entropies –

3rd Law – entropy of a perfect crystal at 0K is zero.

A perfect crystal is very hard to achieve, and Residual Entropy is usually present.

Standard Entropies –

So298 of a compound is the molar entropy at 298K and 1 bar.

For a gas at room temperature:

• Heat from 0 to Tm – ΔSo1 =
• Melt at Tm – ΔSo2 =
• Heat from Tm to Tb – ΔSo3 =
• Vaporisation at Tb – ΔSo4 =
• Heat from Tb to 298K – ΔSo5 =

Then sum the ΔS terms for the absolute standard entropy.

Entropy in Reactions –

ΔSo298 (reaction) = Σvi So298(P) - Σvi So298(R)

(as for enthalpy)

Entropy at another temperature can then be given by:

Free Energy

The factors governing chemical reactivity – enthalpy and entropy.

Spontaneous –

ΔStot = ΔSsys + ΔSsurr > 0

ΔStot = ΔSsys + (ΔHsurr)/T > 0

& ΔHsys = -ΔHsurr, hence:

ΔStot = ΔSsys - (ΔHsys)/T > 0

Therefore for spontaneity,

ΔH – TΔS < 0.

Gibbs and Helmholtz

Gibbs Free Energy is at constant T and p (more useful practically).

G = H – TS

This is a state function. ΔG < 0 for spontaneous process.

Helmholtz is for constant V and T. ΔA < 0 for a spontaneous process.

A = U – TS

i.e. for a spontaneous process, you want to lower the free energy.

Consider infinitesimal changes:

G = H – TS = (U+pV) – TS

dG = dU + pdV + Vdp – TdS – SdT

& dU = dq + dw = dq – pdV

& dS = dq/T → dU = TdS – pdV.

Hence,

dG = Vdp – SdT.

        i.e.

Similarly,

dA = dU – TdS – SdT

dA = dq + dw – Tds – SdT

Assuming Reversible work done,

dA = TdS + dwmax – TdS – SdT

dA = dwmax at constant T

Thus for a system, wmax = ΔU – TΔS. The entropy of surroundings will always increase to compensate for a decrease in the system.

dG = dH – TdS – SdT

dG = dU + pdV + Vdp – TdS – SdT                dH = dU + pdV + Vdp

dG = dq + dw + pdV + Vdp – TdS – SdT                dU = dq + dw

dG = TdS + (dwadd – pdV) + pdV                        dq = TdS.

dw = dwadd – pdV for non-expansion work.

dG = dwadd + Vdp – SdT

dG = dwadd at constant p and T

Endoergic compound has ΔfG > 0.

Temperature dependence of G:

This is the Gibbs-Helmholtz Equation.

Also,

dU =

And,

dU = T dS – p dV

Thus,

T =           &        - p =

Thermodynamic Activity –

Effective concentration:

G = Go + nRT ln a

for an ideal gas.

The effect of pressure on a solid / liquid is negligible, so:

G ≈ Go → apure solid = apure liquid = 1

Variation of G with concentration (for a condensed phase system) –

Concentration = moles per unit volume, and p = RT (n/V),

Gi = Gio + nRT ln [i]

Equilibrium

A system comes to equilibrium when it reaches a minimum of free energy.

αA + βB → γC + δD

= K at equilibrium.

If ΔG < 0 or Q < Kp → forward reaction.

If ΔG > 0 or Q > Kp → reverse reaction.

If ΔG = 0 or Q = Kp → equilibrium.

Relating G & K:

A + B → C + D

ΔG(reaction) = (GC+GD) – (GA+GB)

GA = GAo + RT ln aA

→ ΔG(reaction) = ΔG0(reaction) + RT ln Q

ΔGo(reaction) + RT ln K = 0 at equilibrium.

Hence,

ΔGo = - RT ln K

Chemical Potential

GA = GAo + RT ln aA

This implies that the free energy of a component is independent of all other components of the mixture. This is reasonable for ideal gases only.

This is the definition of the chemical potential (i.e. the partial molar free energy of component A).

Pure substance, μA = G, i.e. dG = μA dnA.

Generalised to:

dGp,T = Σi μidni

dG = Vdp – SdT + Σi μidni

GA = GAo + RT ln

Consider at equilibrium,

dG = 0, therefore:

μA dn = μB dn → μA = μB

i.e. at equilibrium, chemical potential of reactants = products.

ASIDE: Mole Fractions

e.g. N2O4 (g) ⇌ 2NO2 (g)

Let 1 mole of N2O4 reach ⇌ at a pressure ptot such that α moles of N2O4 have reacted.

At equilibrium, (1-α) moles of N2O4 left, and 2α moles of NO2 formed.

Total moles of gas therefore = (1-α) + 2α = (1+α) moles.

Hence,

x is the mole fraction,

Effect of pressure on equilibrium:

K does not depend on p. Position of equilibrium does (as illustrated by the result above).

Effect of temperature on equilibrium:

G = ΔH – TΔS and dGp,T = Σiμidni

ln K =

Assume ΔHo and ΔSo independent of T:

ln K = constant -

Note the linear relation between ln K and 1/T. This is the Van’t Hoff Equation.

Phase Equilibria

Definition: Phase – part of a system which is homogeneous throughout and separated from other phases by a definite boundary.

Vapour → only one phase (irrespective of number of components).

Liquid → Many phases possible (never > number of components).

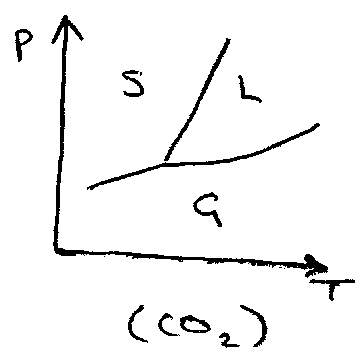
Solid → single component may exhibit many phases, e.g. carbon.

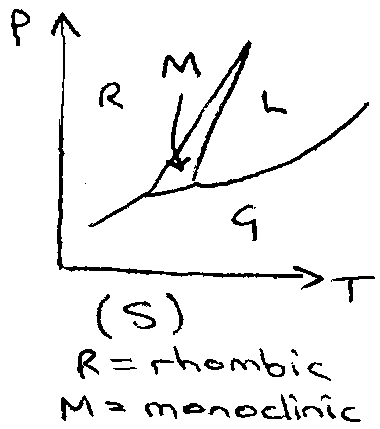
Single component phase diagrams:

T = triple point – all 3 phases in equilibrium.

C = critical point – maximum T at which a gas can be liquefied merely by increasing pressure.

e.g. heat liquid in a sealed container – does not boil. Density of the vapour increases as more liquid evaporates until at TC, density of vapour = density of liquid.

Fluids with temperatures and pressure above TC are called supercritical fluids, SCFs. Properties of these phases are a mixture of vapour and liquid.

Quantitatively,

Consider 2 phases of a pure material in equilibrium, e.g. water and water vapour at fixed T, p, e.g. p = po, T = 373K.

For the two phases a and b,

G = Ga + Gb must be at a minimum, so dG = dGa + dGb = 0.

Hence,

dG = Gma dn + Gmb dn = 0

dG = (Gmb - Gma) dn

i.e. Gma = Gmb at equilibrium.

More generally,

μα = μβ, μ =

Gm(l) < Gm(g) at low T

= - S < 0

Sm(l) < Sm(g)

ΔHm = T ΔSm

(NB: applies only when system is in equilibrium).

How Does Equilibrium responds to changes in T and p?

Changing only one will shift system from equilibrium point.

Must change both to maintain Gmα = Gmβ 

Using:

dGmα = Vmα dp – Smα dT

Vα dp – Sα dT = Vβ dp – Sβ dT

This is the Clapeyron Equation, and is an exact relationship (applicable to all phases).

For solid to gas and liquid to gas, equilibria can be approximated:

ΔV = V(g) – V(l) ≈ V(g) ≈ RT/p

(dp/dT) = pΔH/RT2

Using:

This is Clausius-Clapeyron Equation, and is an approximation. It can used on Phase Diagrams to quantify the gradients, e.g.

This is e.g. for CO2. Assuming ΔH, ΔV independent of T,

s↔l, p2 = p1 + ΔH/ΔV ln (T2/T1)

l↔g & s↔g,

Standardise – Tb and 1 bar.

Measure entropy of vaporisation from intercept of ln p vs. 1/T.

Many liquids have ΔSovap ≈ 85 J K-1 mol-1. This is Trouton’s Rule.

Rationalised as, in absence of specific structural features, most liquids have similar structures, implying same change in structural order would take place on vaporisation.

Deviations – specific features in chemical bonding of system, e.g. H-bonding.

Vapour ordered (acetic acid) → ΔSovap decreases compared to 85.

Liquid ordered (H2O) → ΔSovap increased compared to 85.

Solutions and Mixtures

Partial Molar Gibbs Energy,

G = μApA + μBpB for a binary mixture.

For an open system, G dependent on p, T, n. Thus,

dG = V dp – S dT.

Allowing for change in composition,

dG = V dp – S dT + μAdnA + μBdnB …

At constant p, T:

dG = μAdnA + μBdnB + … (i.e. eliminates first 2 terms of the equation).

So maximum amount of non-expansive work:

dwmax = ΣμAdnA

Since chemical potential depends on composition, for a binary system:

dG = μAdnA + μBdnB + nAdμA + nBdμB

(for an infinitesimally small change).

So,

nAdμA + nBdμB = 0

Therefore, chemical potential of one component cannot change independently of the other.

Thermodynamics of Mixing –

Prior to mixing,

Gi = nAμA + nBμB

Gi = nA (μAo + RT ln p) + nB (μBo + RT ln p)

Following mixing, and using partial pressures,

Gf = nA (μAo + RT ln pA) + nB (μBo + RT ln pB)

Free energy of mixing, Gf – Gi:

ΔGmix = nA RT ln (pA/p) + nB RT ln (pB/p)

Using mole fractions (nJ = xJn):

ΔGmix = nRT (xA ln xA + xB ln xB)

Hence, ΔG is always negative for perfect gases, and ΔGmix is independent of total pressure.

Consider 2 liquids A and B at constant p and T.

Mixing nA of A with nB of B:

• Gibbs before mixing = nAGA + nBGB
• Gibbs after mixing = (nA+nB)GAB
• ΔGmix = [(nA+nB)GAB] – [nAGA + nBGB]
• ΔGmix = [GAB] – [xAGA + xBGB]

For mixing, ΔGmix must be negative.

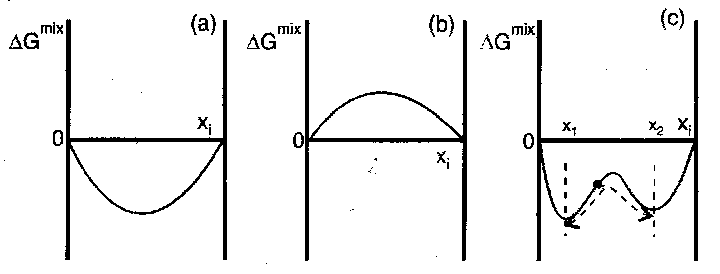
Three possibilities:

1. ΔGmix < 0 for all compositions implies mix in all proportions at the specified temperature – completely miscible.
2. ΔGmix > 0 for all x → immiscible.
3. ΔGmix < 0, therefore expect miscible. However, if x1 < x < x2, then a less negative ΔGmix will result if the mixture separates into phases with composition x1 and x2. Hence, it is partially miscible.

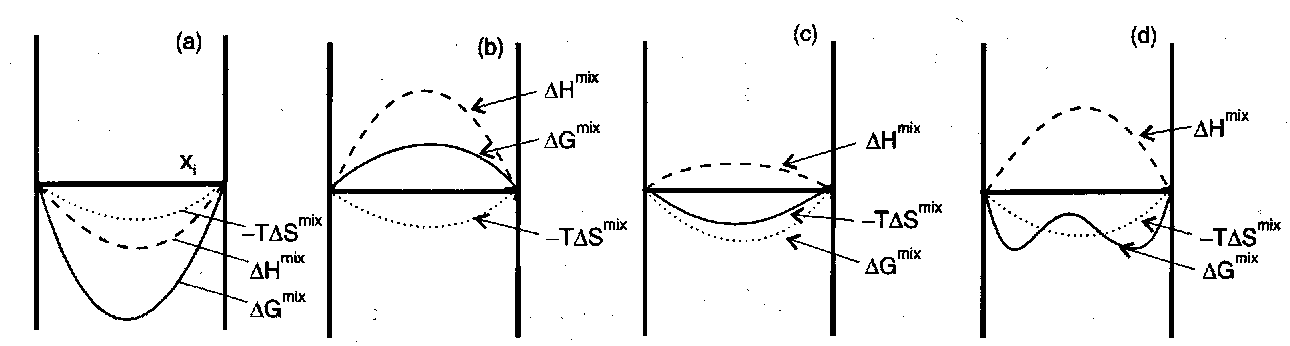
How this arises – consider H and S:

ΔHmix = HAB – (xAHA + xBHB)

ΔSmix = SAB – (xASA + xBSB)

Generally, ΔSmix > 0 (more disordered than pure).

Thus, -TΔSmix contribution to ΔGmix is favourable.

So ΔHmix usually determines miscibility.

1. ΔHmix < 0. Exothermic.
2. ΔHmix > -TΔSmix (any composition → no mixing). Endothermic.
3. Endothermic but ΔHmix < -TΔSmix so ΔGmix < 0 so miscible also.
4. Concentration dependence of ΔHmix has particular form.

Temperature Dependence –

1. and (c) – the TΔS term has no effect – still miscible at all temperatures (changes magnitude of ΔGmix but not sign).
2. ΔSmix dominates at high temperature – immiscible at low temperatures, but miscible at high temperatures. The transition temperature → Upper Critical Solution Temperature (UCST).

Note that it is possible for ΔSmix to be negative. When the 2 components have some kind of strong interaction, such as H-bonding implies higher order when mixed.

However, this is usually overcome by a high ΔHmix associated with strong interactions. In this case, entropy favours phase separation as temperature increases → a lower critical solution temperature (LCST).

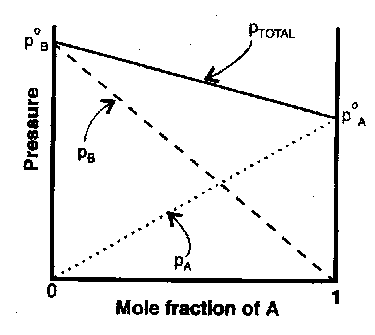
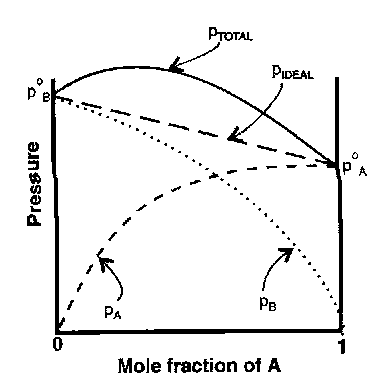
Vapour-Liquid Behaviour –

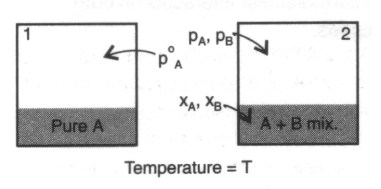
At equilibrium the chemical potential of a substance in a liquid must equal that of the vapour. Since vapour pressure of pure liquid is pA*

μ*A = μoA + RT ln pA*

For a solute,

μA = μAo + RT ln pA

So,

μA = μAo + RT ln (pA/pA*)

If ratio of partial pressures is proportional to the mole fraction in the liquid mixture:

pA = xApA*                [ Raoult’s Law ]

                        

Mixtures that follow the law throughout composition range are ideal solutions.

Ideal dilute solutions obey Henry’s Law at low concentrations.

Ideal Solution:

When these two are brought into equilibrium:

μA(gas, pAo) = μA(pure liquid A)

μA(gas, pA) = μA(mixture at xA)

Hence,

μA(gas, pA) - μA(gas, pAo) = RT ln (pA/pAo)

μA(mixture, xA) - μA(pure A) = RT ln (pA/pAo)

μA = μAo + RT ln xA

Also,

Gp,t = ΣI μini

ΔGmix = RT ΣI xi ln xi

Using:

ΔGmix = ΔHmix – TΔSmix = 0 – TΔSmix

i.e.

ΔSmix = - R Σi xi ln xi

Thus, for an ideal solution, molecules must be:

• similar in chemical nature (similar intermolecular forces)
• similar in size and shape.

The 2nd of these → no overall volume change on mixing:

ΔVmix =

Non-ideality –

μA = μAo + RT ln aA

For real solutions, aA ≠ xA, aA = γAxA

γI =

γ tells us how much it has deviated from ideality.

Generally, interactions in solution are weaker than in pure liquids – more easily escape to the vapour.

Actual vapour pressure > ideal vapour pressure.

Opposite case – strong interactions e.g. H-bonding.

Solid-Liquid Phase Equilibrium

Solute A and solvent B.

Solid A ⇌ Liquid (A+B) – solid A comes out of solution leaving a saturated solution of A in B.

This represents the solubility limit of the solute in the solvent.

Solid B ⇌ liquid (A+B) – solvent starts to freeze. This represents the freezing point of the solution.

Solid A ⇌ Solution of A.

μAo(solution) = μA(solution) = μAo(liquid) + RT ln aA.

μAo(solution) - μAo(liquid) – RT ln aA.

ΔGAfus = ΔHAfus – TΔSAfus = RT ln aA.

Therefore,

ΔHAfus – T ( ) = RT ln aA.

ln aA =

Ideal, aA = xA.

Note only terms involving A.