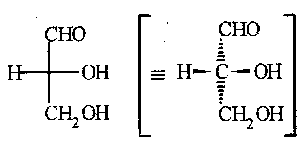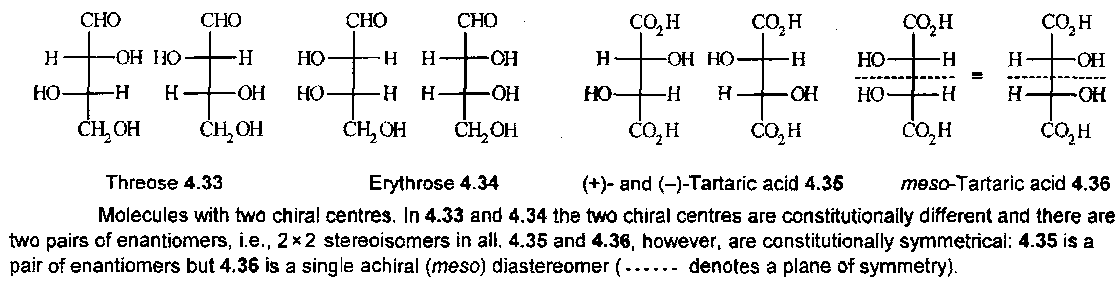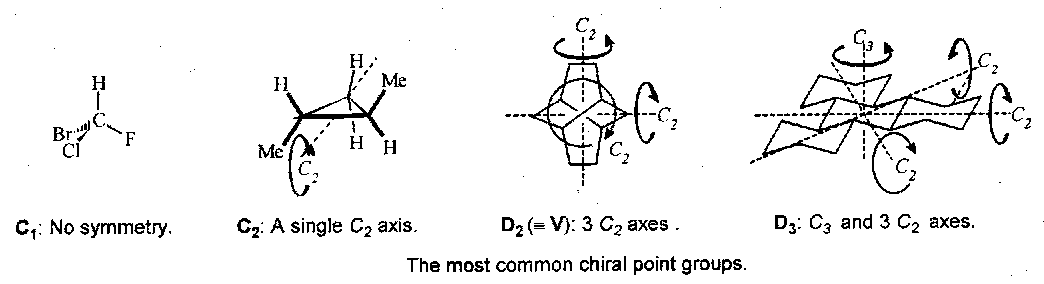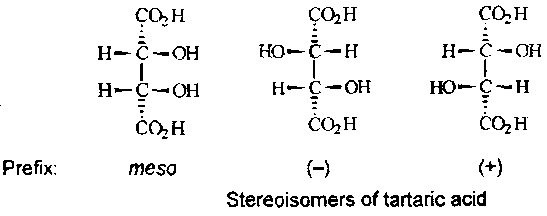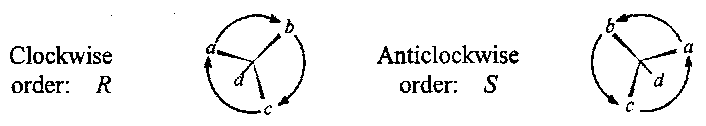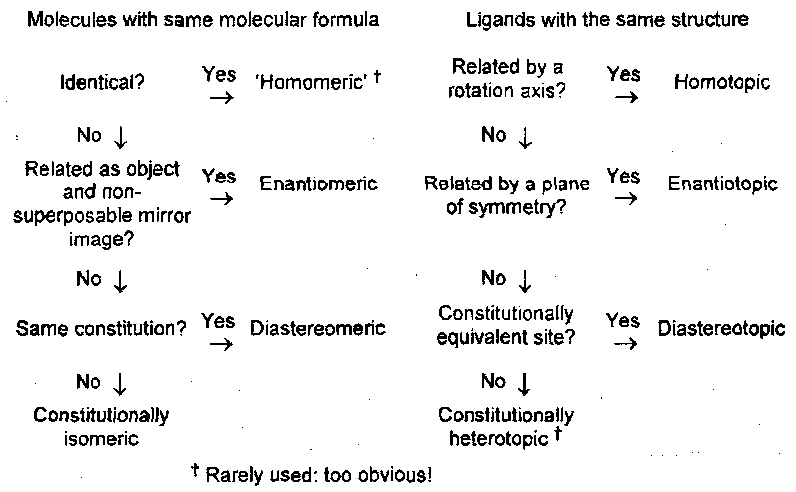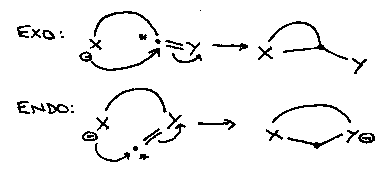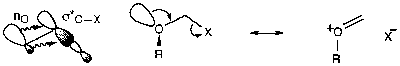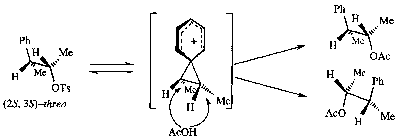Stereochemistry And Stereoelectronics Notes

Stereochemistry in Organic Molecules

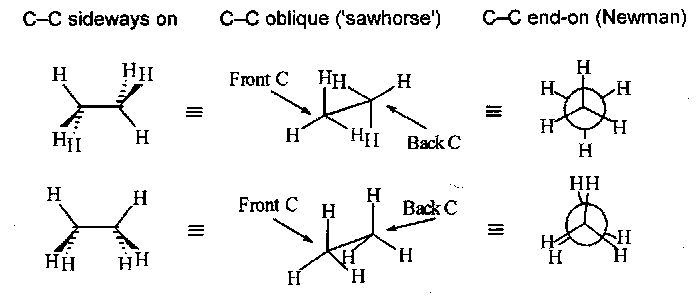
Conventions used in drawing molecules

Also, Fischer projections can sometimes be useful for acyclic molecules with chiral centres. The carbon chain is drawn vertical with the most oxidised atom at the top. By convention the vertical bonds from the implied central C atom go back, behind the plane of the paper, while the horizontal bonds come forward.

Clearly, a Fischer formula must not be:

1. rotated through 90o in the plane of the paper, nor
2. flipped over, i.e. rotated through 180o out of the plane of the paper.

A Fischer formula may be rotated through 180o in the plane of the paper.

They can also be used for two or more chiral centres with, conventionally, the longest carbon chain vertical, the bonds to top and bottom atoms or groups go back, and all the atoms or groups to one side or the other come forward.

If the Fischer formula has a horizontal plane of symmetry he compound is a meso isomer and achiral. The number of stereoisomeric compounds is obtained by enumerating all the distinguishable Fischer formulae, bearing in that:

1. rotation through 180o in the plane of the paper, and
2. cyclic exchange of three ligands on a chiral C atom

are both permitted.

4.33 and 4.34 are each a pair of enantiomers and they cannot be interconverted by any low energy route. In contrast, 4.36 represents a single achiral compound in which the two halves of the molecule are related by a mirror plane in the Fischer formula. 4.36 is called meso-tartaric acid.

Symmetry in molecules

Chiral Point Groups

Symmetry elements in chiral point groups must all be simple rotation axes.

Also, T, O and I.

Achiral Point Groups

Identical with its mirror image. Any point group with one or more of the elements σ, i and Sn is achiral:

This includes, Cnv, Cnh, Dnd, Dnh, Td, Oh and Ih.

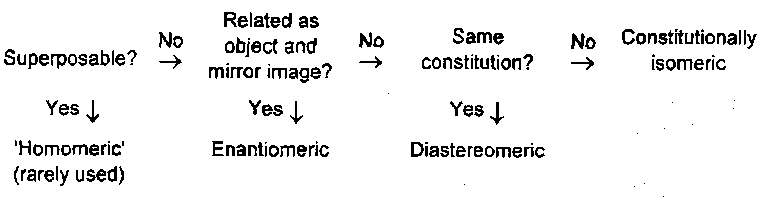
Classification of Isomerism in Compounds

The possible relationships between two molecules with the same molecular formula are:

Diastereomeric molecules or compounds differ in all properties that depend on structure. It is only when we define the constitutions of molecules in terms of single, double bonds etc that we distinguish between diastereoisomers and constitutional isomers. Thus, always use the term structure to include stereochemistry, otherwise use the term constitutional isomer.

The relationship between the terms enantiomeric/diastereomeric and enantiomer/diastereomer

Enantiomeric and diastereomeric are defined as mutually exclusive by the diagram above. Enantiomer and diastereomer are not necessarily though. For example, there are three stereoisomers tartaric acid: (+)-tartaric acid is both the enantiomer of (-)-tartaric acid and a diastereomer of meso-tartaric acid:

Stereogenic Units in Molecules

A molecule has a stereogenic unit (e.g. a chiral centre, axis, or plane, or a double bond, etc) if exchange of an appropriate pair of ligands generates an stereoisomer.

The most common is the chiral centre, e.g. carbon with four different ligands coming from it.

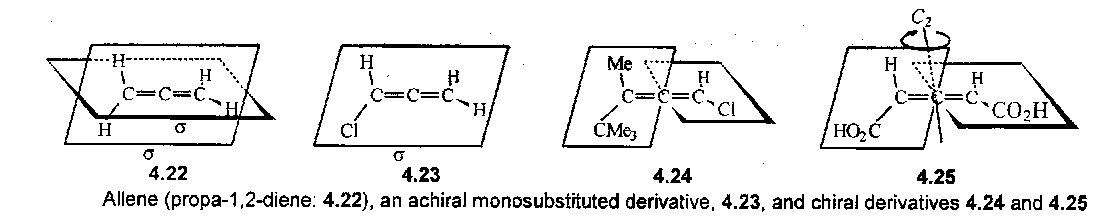
A chiral axis is for example found in allenes:

Note that 4.22 has two planes of symmetry. In order to eliminate these and generate a chiral molecule it is necessary that substituents at each end of the C=C=C unit be unlike, as in 4.24 and 4.25. Unlikely substituents at one end leaves a symmetry plane as in 4.23.

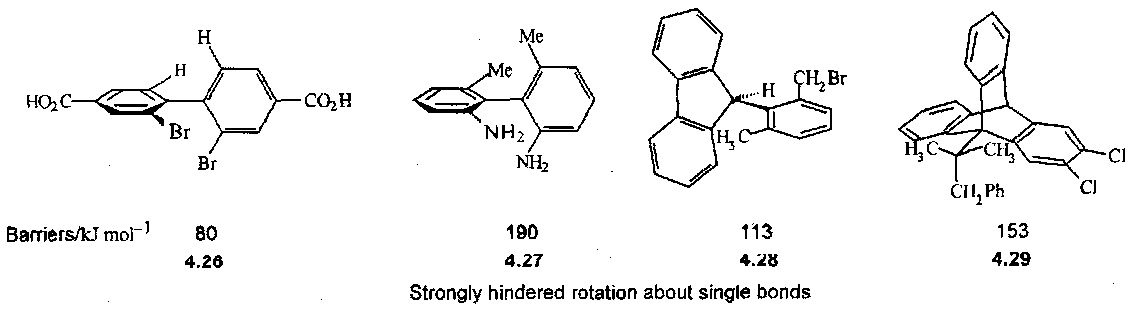
The C=C=C bonds are strong enough to prevent free rotation. Other chiral axes require bulky groups to prevent rotation, and they are then chiral molecules, e.g.

Chiral planes are rather rare. One example is:

Cahn-Ingold-Prelog (CIP) System

Applicable to tetrahedral carbons with 4 different ligands, or pyramidal molecules (where a “phantom” ligand with atomic number 0 is added at the vacant position).

The absolute configuration of a chiral centre is specified by a prefix R (from the Latin rectus) or S (sinister). The ligands are denoted by the labels a,b,c and d. The molecule is viewed from the base a,b,c. If the labels a,b,c are in a clockwise order the configuration is R. If a,b,c are in an anticlockwise order the configuration is S.

The priorities of the groups are decided by applying the following rules in turn. The process is stopped for a ligand once it has a uniquely defined priority. Each rule is applied exhaustively before passing on to the next rule. You start with the atoms bound directly to the chiral centre, and move away if necessary to differentiate them, following the highest priority branches.

The rules are:

1. Atomic number: higher atomic number has priority, irrespective of number of atoms.
2. Isotopes. Higher mass has priority over lower mass.
3. Double bond configuration: (i) Z has higher priority than E, and (ii) cis has higher priority than trans, where cis and trans refer to the relationship between the substituents that includes the chiral centre and the higher priority group at the other end of the molecule.
4. i (like) has higher priority than u (unlike), and r higher than s.
5. Enantiomeric groups: R has higher priority than S and M is higher than P.

An example, (+)-D-glyceraldehyde:

E and Z Prefixes for Double Bond Diastereomers

The prefixes cis and trans are adequate for simple double bond compounds only. Generally Z and E are used now. The CIP system is used to assign priorities (a>b and a’>b’) to the substituents at each end of the double bond. If a and a’ are on the same side of the double bond then the prefix is Z, otherwise it is E.

Examples:

Topism

Heterotopism is the phenomenon of two or more ligands, constitutionally equivalent and therefore identical in isolation, being distinguishable when part of a molecule. For example, isotopic labelling shows that the two Hs in the CH2 group of ethanol are very different in their enzyme catalysed rates of oxidation (i.e. they are not identical).

Two ligands, identical in isolation, may be distinguishable when part of a molecule. Two such ligands may occupy places that are either equivalent (homotopic) or not (heterotopic). The latter has sub-classes enantiotopic and diastereotopic.

There is a close parallel between classes of isomerism and of topism:

Descriptors for heterotopic ligands

Unfortunately there are two different systems.

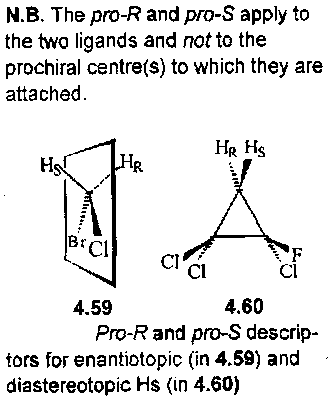
Pro-R and Pro-S descriptors

A C atom with two (stereo)heterotopic ligands is a prostereogenic centre. If changing one of the ligands generates a chiral centre the C atom is prochiral. The two similar ligands on the prochiral centre are given descriptors pro-R and pro-S. A pair of heterotopic ligands have the same priority under the CIP rules.

NB: the pro-R / pro-S applies to the two ligands and not to the prochiral centre(s) to which they are attached.

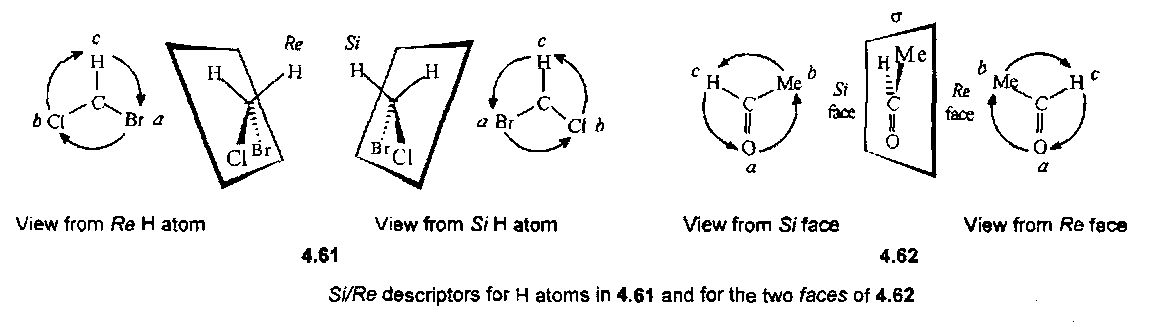
Si and Re nomenclature

A system for defining descriptors for prostereoisomeric centres and heterotopic faces of a trigonal atom uses the plane defined by three different ligands, with priorities a>b>c determined by the CIP rules, to divide space into two regions, labelled Si and Re. The order a,b,c of the ligands is clockwise when viewed from Re space, and anticlockwise when viewed from Si space.

Stereoelectronics of Organic Reactions

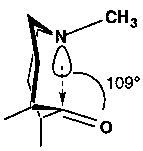
Attack on Carbonyls

N-C-O angle is close to the tetrahedral angle. This is the Burgi-Dunitz angle, and defines the preferred geometry of approach for nucleophilic addition of any nucleophile to a ketone carbonyl.

Baldwin’s Rules

Through-space interactions between two orbitals on the same molecule are subject to geometric constraints imposed by its structure.  When these are two-electron bonding interactions strong enough to lead to reactions such constraints can have major effects on reactivity. The effects are most obvious for cyclisations, and the experimental situation is conveniently summarised in a set of rules by Baldwin.

Note that these “rules” are not really rules, but more of a guide. There are some exceptions to it. It is also worth remembering that they are stereoelectronic and kinetic in origin, so the process may be favourable thermodynamically, but not occur due to a kinetic barrier.

Ring closure reactions can be characterised in terms of three parameters:

5        -        exo        -        trig

(a)                 (b)                 (c)

a) represents the number of atoms in the ring being formed.

b) indicates that the breaking bond ends up outside the final ring – exocyclic, cf. endo:

c) denotes the geometry of the atom being attacked (*) – trigonal (sp2) in this case, cf. tet and dig.

The following rules can then be applied to suggest the favoured or disfavoured nature of ring closure, based on the stereoelectronic requirements of the transition state:

So 5-endo-trig is disfavoured:

The system is flat and little overlap is possible between the nitrogen lone pair and the LUMO (π*) of the sp2 carbon being attacked.

While 5-exo-trig is favoured:

Good overlap between the nitrogen lone pair and π* orbital of the carbonyl group is possible.

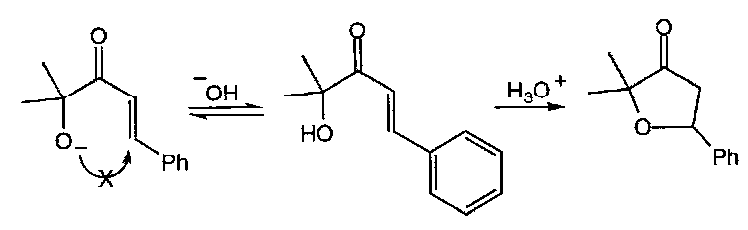
A Common Exception

5-endo-trig in particular is one of Baldwin’s Rules that is often found to occur despite being predicted to be unfavourable. For example, the following reaction does not occur in base, but does in acid:

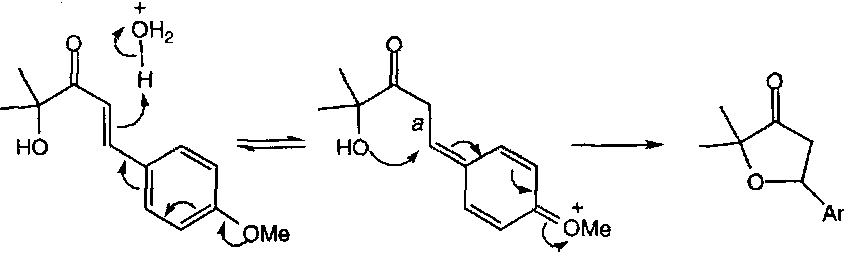
This can be explained either by thinking of the acid form as having a C=OH+ that is sufficiently stabilised by π-delocalisation into the aromatic ring for the cyclisation to qualify as a 5-exo-trig type process, or by looking at an alternative mechanism (which is certainly found to be the case for the 4-methoxy derivative) which involves C-protonation, making this a genuine 5-exo-trig reaction:

The effect of C-protonation is to allow free rotation about the original C=C bond, thus removing the geometrical restriction to overlap.

Anomeric Effect

Electronegative substituents prefer the axial position. For groups such as OH / OR, the effect is comparable with the steric preference for equatorial positions generally observed (see Alicyclic Tutorial), although stronger electronegative groups such as the halogens greatly prefer axial position.

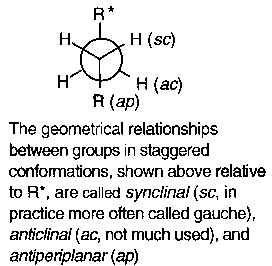
It should be noted also that the anomeric effect is not limited to acetals or ring systems, but is a general stereoelectronic effect. It is typically seen as the gauche effect, where preference for the synclinical (sc) position is shown:

An explanation for this effect is best depicted:

i.e. the geometry is antiperiplanar to accommodate overlap of orbitals in this way.

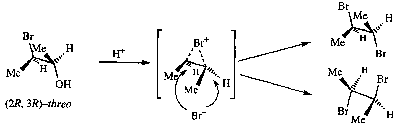
Anchimeric Assistance

This is simply put Neighbouring Group Participation. It is often the case that antiperiplanar alignment or similar is required for this to be effective, and thus this has stereoelectronic consequences.

Anchimeric assistance is when a substituents is capable of stabilising an adjacent carbocation by acting as an intramolecular nucleophile. Typically these are β-substituents with an unshared electron pair or double bond.

Some examples,

Migratory Aptitude

This is the ease with which any particular group will undergo nucleophilic 1,2-shift. It is not really quantifiable since it varies from reaction to reaction (only comparison possible). This comparison can be through reaction rates (when homologous series of substrates, only one type of migrating group, and same conditions). Alternatively the product can be analysed for mixtures of two competing substituents. The latter provides better comparison, but is not always possible (for example if the group must be antiperiplanar, then only that group will ever migrate).

Generally, aryl groups migrate more readily than alkyl, and electron donating substituents on the aryl will increase the propensity for migration. It should be noted though that there are usually many other factors that determine rate and product, such as steric or conformational effects.

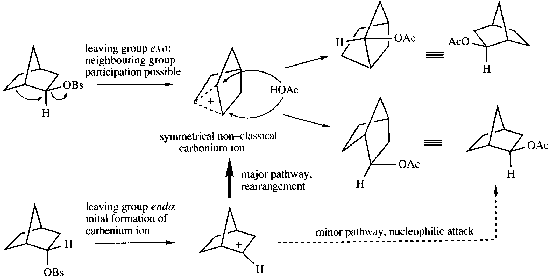
Non-classical Carbonium Ions

Common in strained rings. They are a 2-electron, 3-centred bonds (i.e. they have a 5-coordinated cationic centre).

The classic reaction that shows this is: