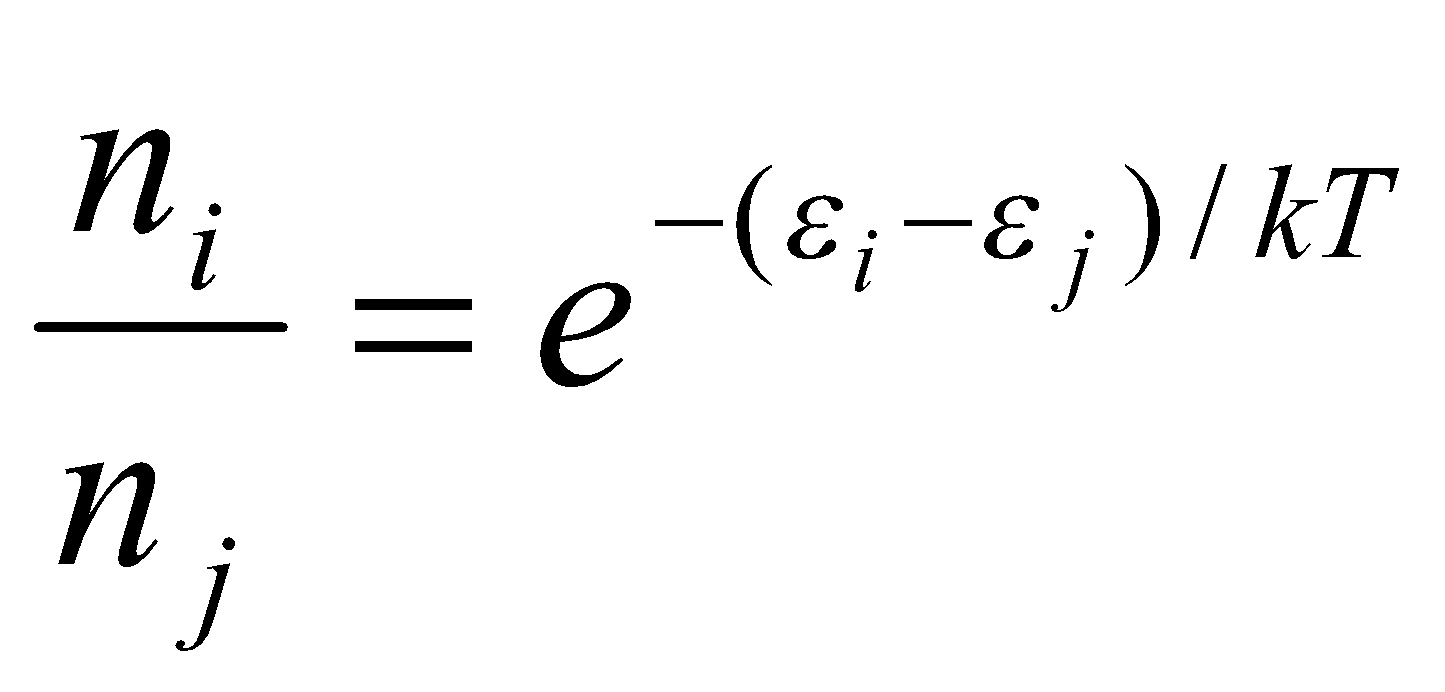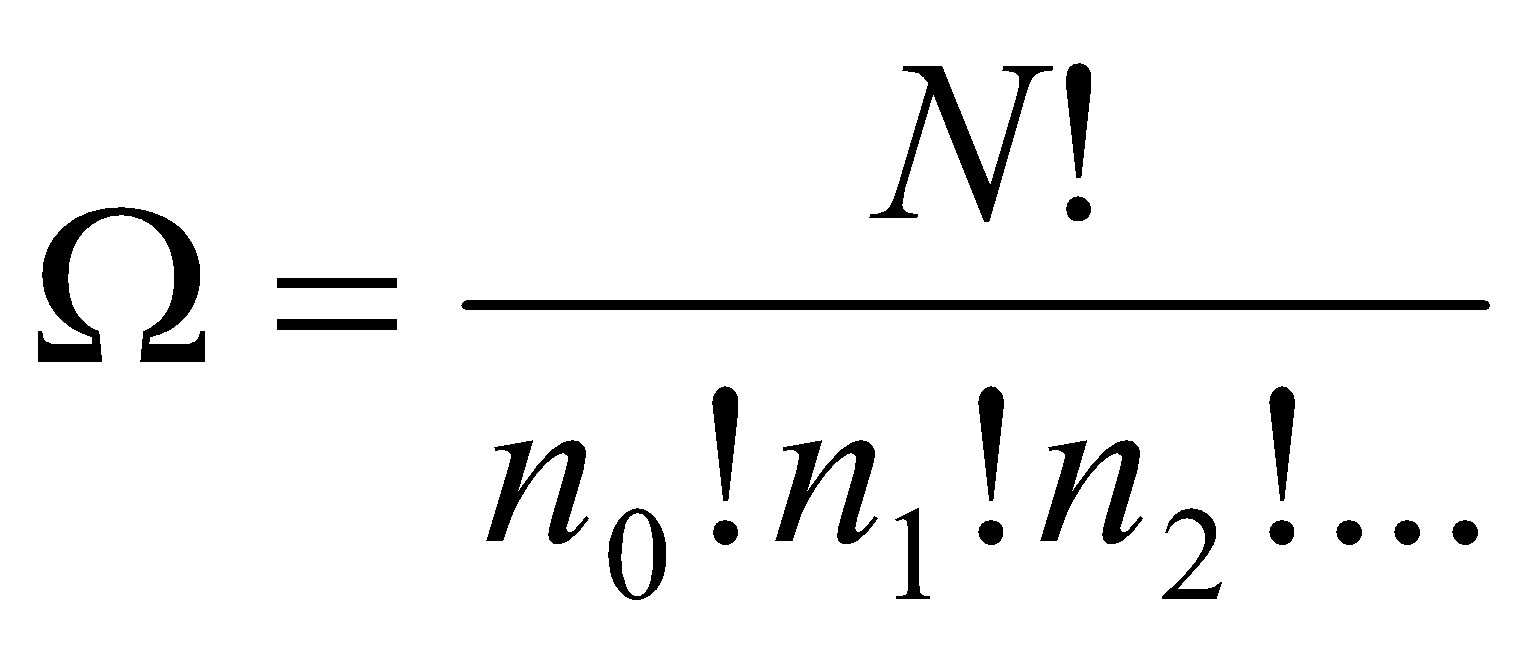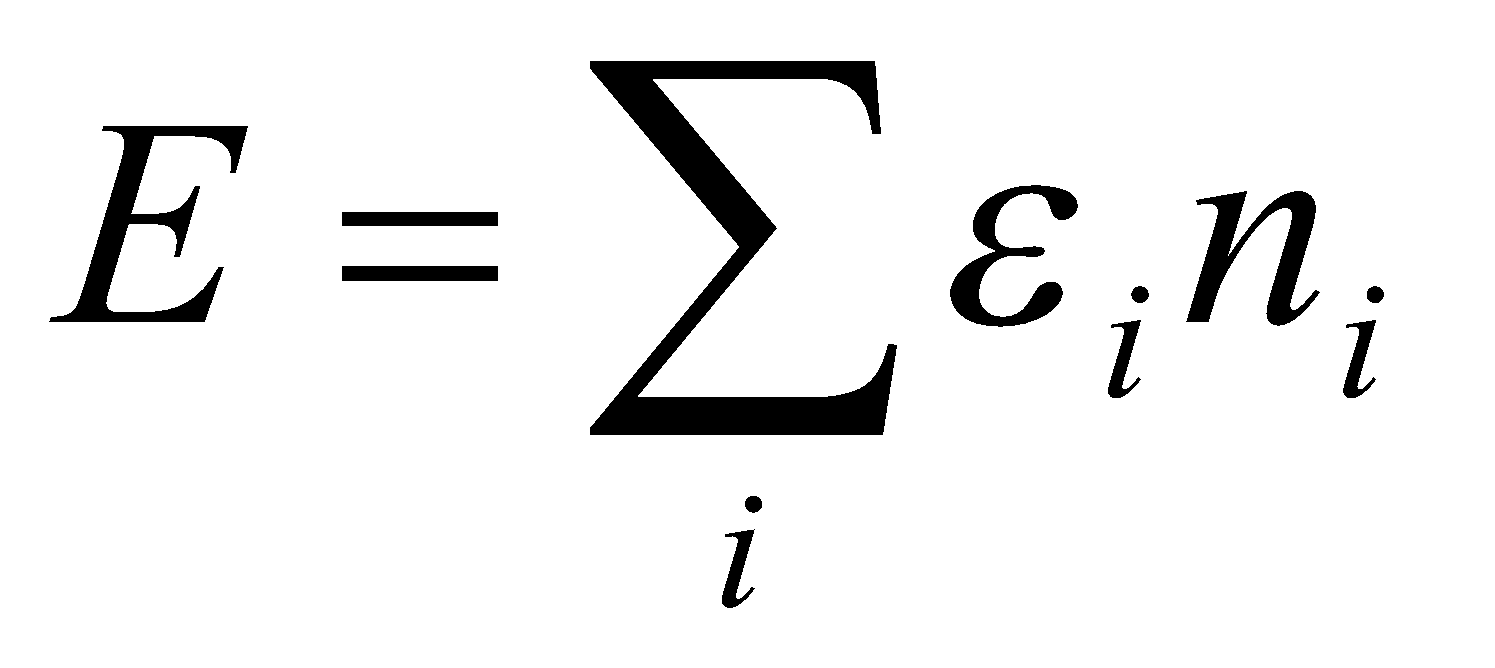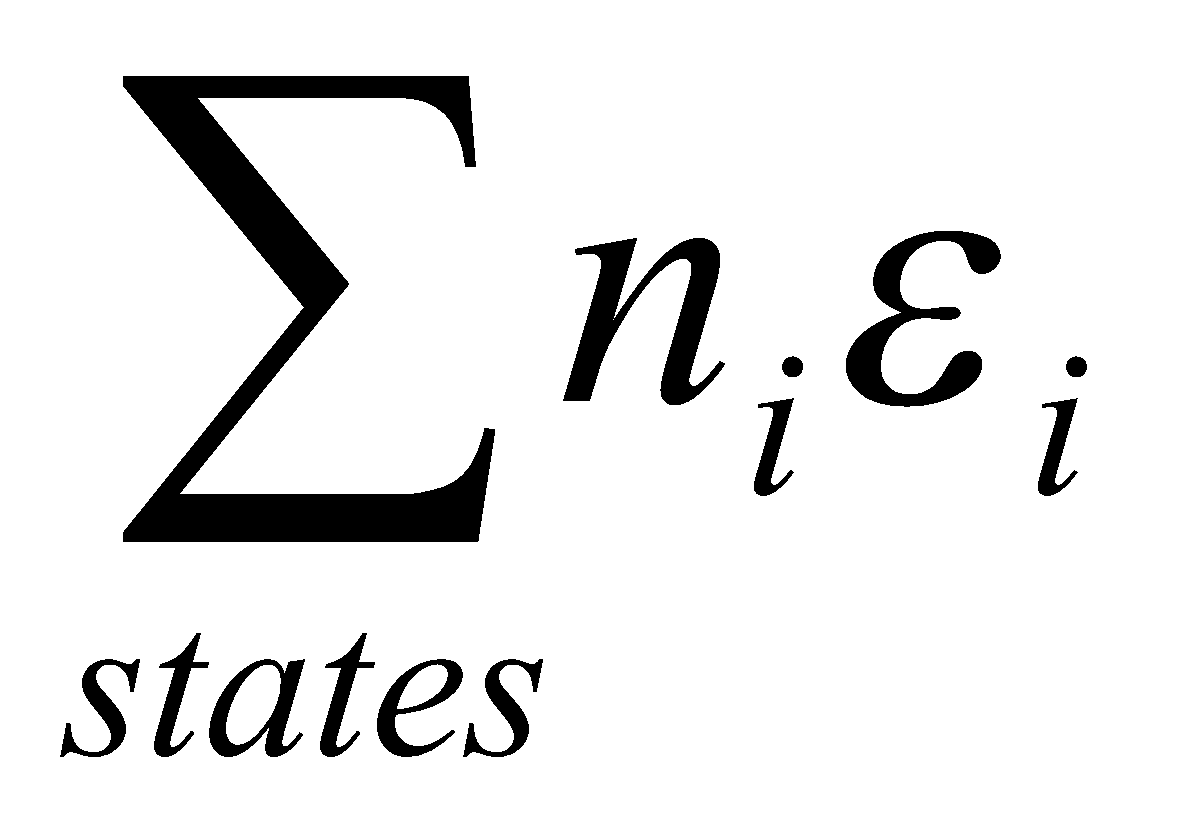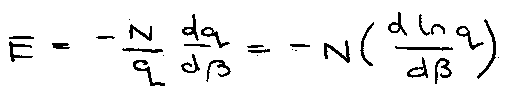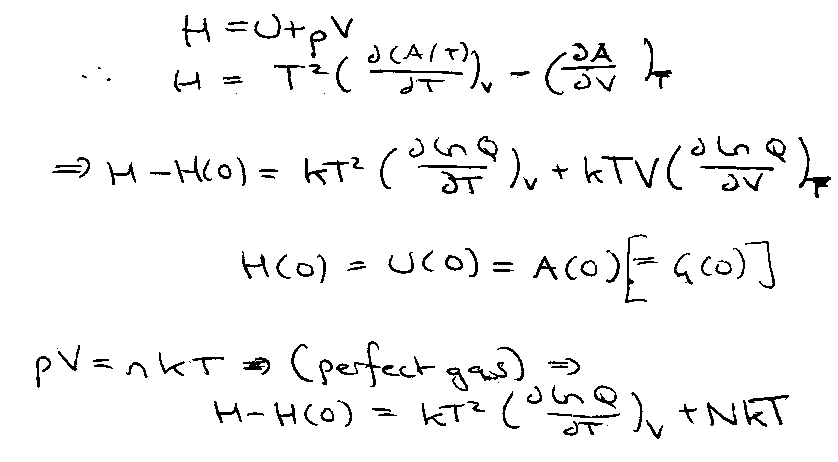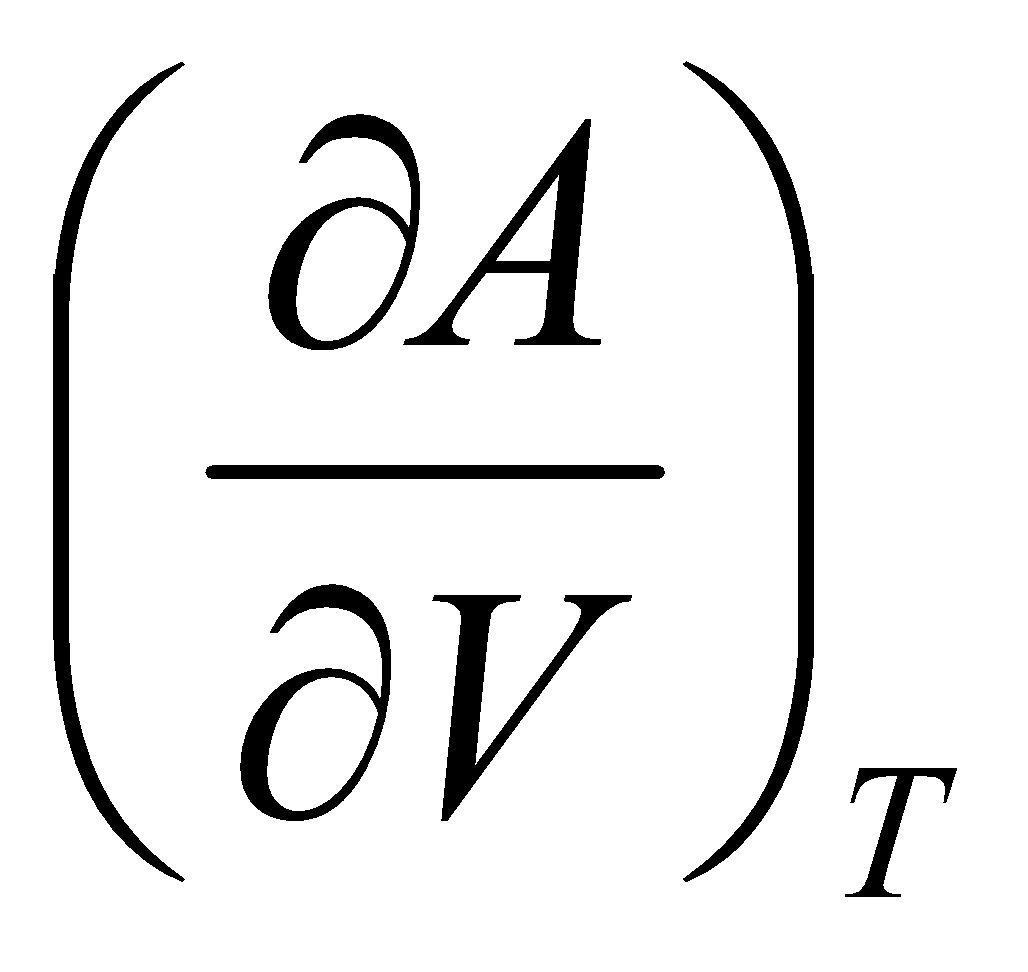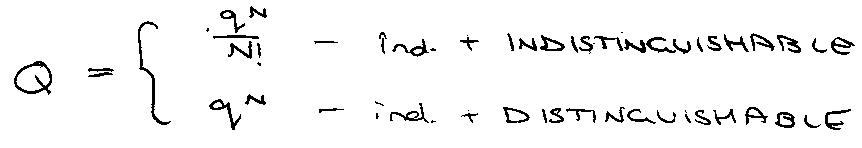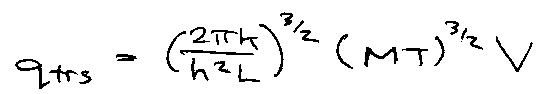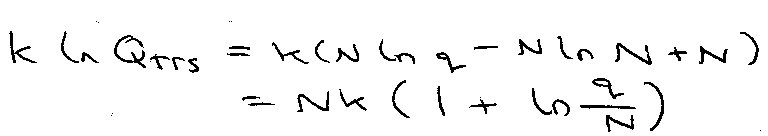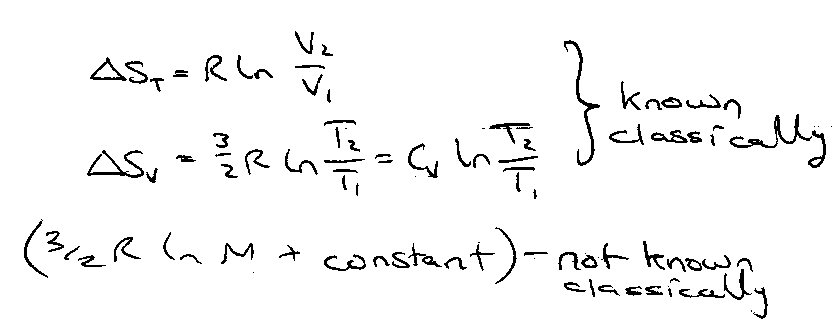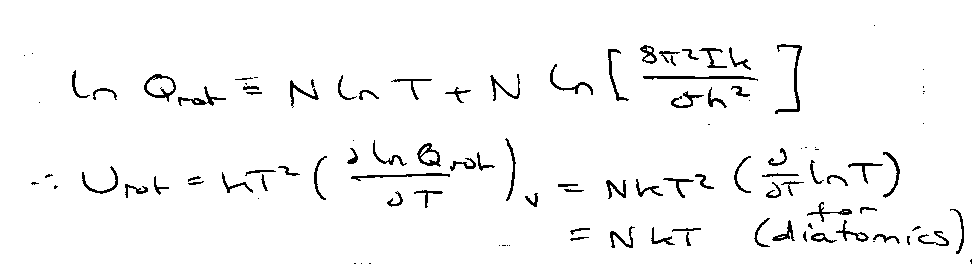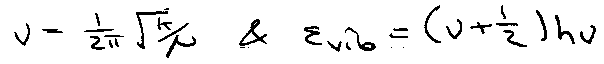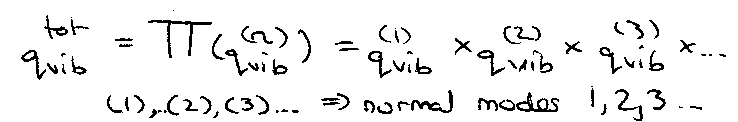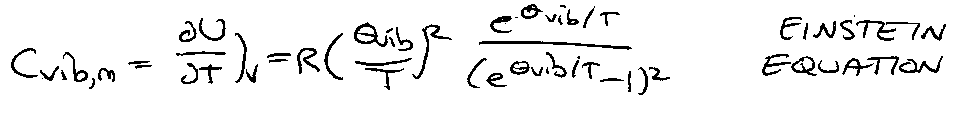Statistical Mechanics Notes

Boltzmann Factor

Physical quantity

Boltzmann Law:

Distinct, Independent Particles –

Distinct → can tell which is which (labels) a,b,c…

Independent → minimal interaction (can exchange energy in collision).

Hence, E = εa + εb + εc + … =

Configurations –

Sharing energy amongst particles from a manifold of energy states, εo, ε1, ε2 … etc (ε0 = 0).

At any instant, there are:

• no particles with εo.
• n1 particles with ε1, etc.

This is the configuration. (Same Total Energy).

Statistical Weights –

Number of ways of reaching a given configuration, Ω. Represents the probability that the configuration can be reached.

, where x! = x(x-1)(x-2)(x-3)…3,2,1 and 0! = 1.

Equal Probability of Configurations –

No bias to any configuration. This is the Principle of equal a priori probabilities.

Conservation of Number and Energy –

        &        

Predominant Configuration –

Configuration with the largest statistical weight.

For very large number of configurations, the average peak of the distribution completely dominates so that everything else is negligible.

Maximisation Subject to Constraints –

Find maximum in distribution (Ω) subject to constraints of Conservation.

Predominant configuration amongst N particles is found to have energy states populated as:

, where α and β are constants under fixed temperature.

Identify α:

This is the T dependent ratio.

β = 1/kT                 [ can be proven, see later ]

Molecular Partition Function

Derived from Boltzmann Law.

Eliminate no (generally not known):

N = no + n1 + n2 + … =

Hence,

Shows how particles distribute (partition) over accessible quantum states.

• Infinite series that converges more rapidly for increasing εi and increasing β.
• Can be evaluated as soon as βε >> 0, so that e-βε → 0.
• If ε1 >> kT, q → 1.
• For successive energy gap Δε, q >> 1 if Δε < kT.

Degeneracy –

Measure extent of particles escaping ground state.

T = 0K, q =1 (no = L).

Increasing T, q → ∞ (fewer particles in Ground State; infinite number of accessible states).

Applications –

Total Energy, E = n1ε1 + n2ε2 + … =

From q:

Note that:

Thus,

Internal Energy –

U = U(0) + E

U = U(0) - N

Also, q depends on V (which depends on T) so must specify constant volume:

This can be combined with the only temperature-dependent term in q for translational energy (see later):

ln q = -3/2 ln β

Such that:

This can be compared to N atoms in a perfect gas:

U = U(0) + 3/2NkT

And hence we see that β = 1/kT                [ as used earlier ]

Entropy –

S = k ln Ω.

U =U(0) + E = U(0) +

At constant V (as for internal energy) the spacing of successive energy states does not change on heating. Thus, dεi = 0,

dU =

From here, dU = dqrev = T dS                 [ classical thermodynamics ]

Condition for max Ω (predominant configuration):

Number of particles is constant: = 0

Therefore,

dS = k d(ln Ω)

S = k ln Ω.

Molecule → Mole (Canonical Partition Function)

Reasonable when assuming non-interacting, and does not apply to other properties, e.g. S.

Allow possibility of interactions by invoking the idea that every system has a set of system energy states which molecules can populate.

Canonical Partition Function, QN :

Hence,

Compare to:

Can continue to develop a statistical toolkit of functions, e.g. Entropy:

Third Law → S0 = 0, on integrating:

Massieu Function

J = - A/T

This gives:

Links Statistical and Classical Thermodynamics.

Also, Pressure:

Heat Capacity,

Entropy:

Enthalpy:

Gibbs Free Energy:

G = A + pV

G = A – V

Perfect Gas →

G – G(0) = - kT ln Q + nkT.

Chemical Potential:

Independent Systems:

Use Stirling’s Approximation:

ln N! ≈ N ln N – N

e.g.

–kT ln Q = -NkT ln q + NkT ln N – NkT

Thus,

G – G(0) = -NkT ln (q/N)                [ For INDISTINGUISHABLE ]

G – G(0) = -NkT ln q                [ For DISTINGUISHABLE ]

Translational Partition Function, qtrs

Consider particle in a box:

Sum over all accessible states:

But practically all energy levels densely packed, so becomes an integral:

Canonically,

Collecting constants,

Thermodynamic Functions for an Ideal Monatomic Gas

Thus, derivatives simple:

These can then be used in the functions found earlier. Hence,

Entropy more complex, since ln Qtrs appears. It proceeds as:

Use Stirling’s Approximation: ln N! ≈ N ln N – N

Thus,

Overall,

One mole of Ideal Gas →

This is the Sackur-Tetrode Equation. The constants add up to 172.29 J K-1 mol-1 [ 20.723R ]

Note that:

Ideal Diatomic Gas – Rotational Partition Function.

For a rigid rotor:

If I is not too small and T not too low, then appreciable number of rotational states are occupied, and there is a virtual continuum as for qtrs:

Problems tend to arise when T is nearly 0K and the molecule contains Hydrogen.

This expression otherwise works for all heteronuclear diatomics. Special considerations required for homonuclear diatomics. This is due to over-counting of rotational states by a factor of 2. This is because 180o rotation of X-X gives a result indistinguishable from 360o.

There qrot/2 required for all linear symmetric molecules.

Or,

qrot = T/σθr

Where:

σ = symmetry factor (= 2 for homonuclear diatomic, = 1 for heteronuclear diatomic).

σ = 2 for H2O and σ = 3 for NH3, for example.

Quantum Mechanically,

Interchange of identical nuclei may leave ψ unchanged, i.e. symmetric, or ψ → -ψ → antisymmetric.

Symmetric → boson (integral), while antisymmetric → fermion (half-integral).

ψtot =ψtrs.ψrot.ψvib.ψel.ψns

ψns = nuclear spin wavefunction. Symmetric or antisymmetric depending on whether 2 nuclear spin states are parallel / antiparallel.

ψrot = antisymmetric or symmetric. For even J it is symmetric, for odd J it is antisymmetric.

ψel = antisymmetric or symmetric. Homonuclear diatomic is usually 1Σg+ = symmetric. Only O2 is common exception, 3Σg- is antisymmetric.

ψtrs = only motion of centre of mass, so no effect on symmetry (symmetric).

ψvib = only depends on internuclear distance (symmetric).

Thus, in hydrogen I = ½ and the nucleus is a fermion so the ψtot is antisymmetric.

This requires odd J to give symmetric nuclear spin and even J to give antisymmetryic.

In Deuterium, I = 1 (boson) → ψtot is symmetric. Thus,

Odd J → paired nuclear spin.

Even J → parallel nuclear spin.

Thermodynamic Functions with qrot:

Applies to all linear molecules with only two degrees of freedom in rotation.

Molar → Urot = RT, Crot,m = R.

For entropy,

Extending to polyatomic, non-linear molecules – must consider 3 independent motions of inertia:

Ortho and Para Spin States

In general, for homonuclear diatomic with nuclear spin I, each nucleus have p (=2I+1) spin states, and a total of p2 nuclear spin wavefunctions to include in ψrot.

Of these p2,

½ p(p+1) = symmetric                        [ ORTHO ]

½ p(p-1) = antisymmetric                [ PARA ]

This is true whether they are bosons or fermions.

Proton, I = ½ , ψtot = antisymmetric.

2 spin states, ↑ or ↓, therefore 4 ψns (p2)

Thus,

3 ortho (symmetric)         =        ODD J                        [ o-Hydrogen ]

1 para (antisymmetric)         =        EVEN J                        [ p-Hydrogen ]

Deuteron, I = 1, ψtot = symmetric.

3 spin states per nucleus, so 9 per molecule (p2)

6 x ortho (symmetric)        =        EVEN J                        [ o-Deuterium ]

3 x para (antisymmetric)        =        ODD J                        [ p-Deuterium ]

Therefore ortho-Hydrogen → Odd J, 3:1 ratio with odd predominating (due to statistical weight).

Similarly, ortho-Deuterium → Even J, 6:3 ratio with even predominating.

Ratios apply to e.g. rotational Raman Spectrum.

At high temperatures, hydrogen exists in an equilibrium mixture of spin states favouring o-Hydrogen by 3:1.

At low temperatures, there is an increased tendency for J = 0. Even → switch to p-Hydrogen. This conversion is slow.

Normal Hydrogen (n-H2) = 3:1 mixture.

Nuclei with zero spin –

Some nuclei are I=0 (e.g. 16O).

8 protons and 8 neutrons occupy their own energy manifolds (closed shell configurations – all spins paired). Also true for 12C.

p = 2I + 1 → O2 or CO2 have only 1 spin state.

I = 0 → integral, therefore boson, so ψtot = symmetric.

Hence,

CO2 → only even J.

O2 → only odd J.

Reason now is that ground electronic state is 3Σg- (i.e. antisymmetric), therefore rotation must also be antisymmetric (odd), unlike CO2.

Vibrations in an Ideal Diatomic, qvib

Orders of magnitude: qvib > qrot > qtrs are usually in the ratio 1:10:250-300 orders of magnitude. Thus, cannot use the continuum approximation for qvib.

qvib @ 300K ≈ 1.

Simple Harmonic –

Always non-degenerate in diatomics. Not so for polyatomics – linear → (3N-5) normal vibrational modes, while non-linear → (3N-6).

εο = 0, ε1 = hv, ε2 = 2hv, etc, due to reference against ground state of ½hv. Thus,

This gives a geometric series:

This is true for diatomics only. For polyatomics, just consider each normal mode of vibration separately.

Vibrational Energy spacings are much larger than Rotational, therefore θvib ≈ 102-103, θrot ≈ 101-102.

Polyatomics –

Independent and factorisable, therefore ignore anharmonicity (except at high T).

High Temperature Limit –

At high T, linear in qvib against T.

Expand :

Thermodynamic Functions –

Note: far less simple than Utrs and Urot.

At high T: Uvib,m = RT        (for each normal mode)

At 300 K: Uvib,m =

Also note that if ε0 is set to ½hv instead, then must add this to the result.

Heat Capacity –

Entropy –

Electronic Partition Function

Ground States are commonly degenerate (not O2 though, g1 = 1).

For Atoms, use (2S+1)ΓJ and go = 2J+1.

For molecules, use (2S+1)Γ and go = 2S+1.

Excited States can be approached in a similar manner.

Usually, the energy gap from ground state to 1st excited state is large and the above applies. If the gap is not negligible compared to kT (i.e. θel/T << 1) then:

(Higher states than the 1st are rarely occupied).