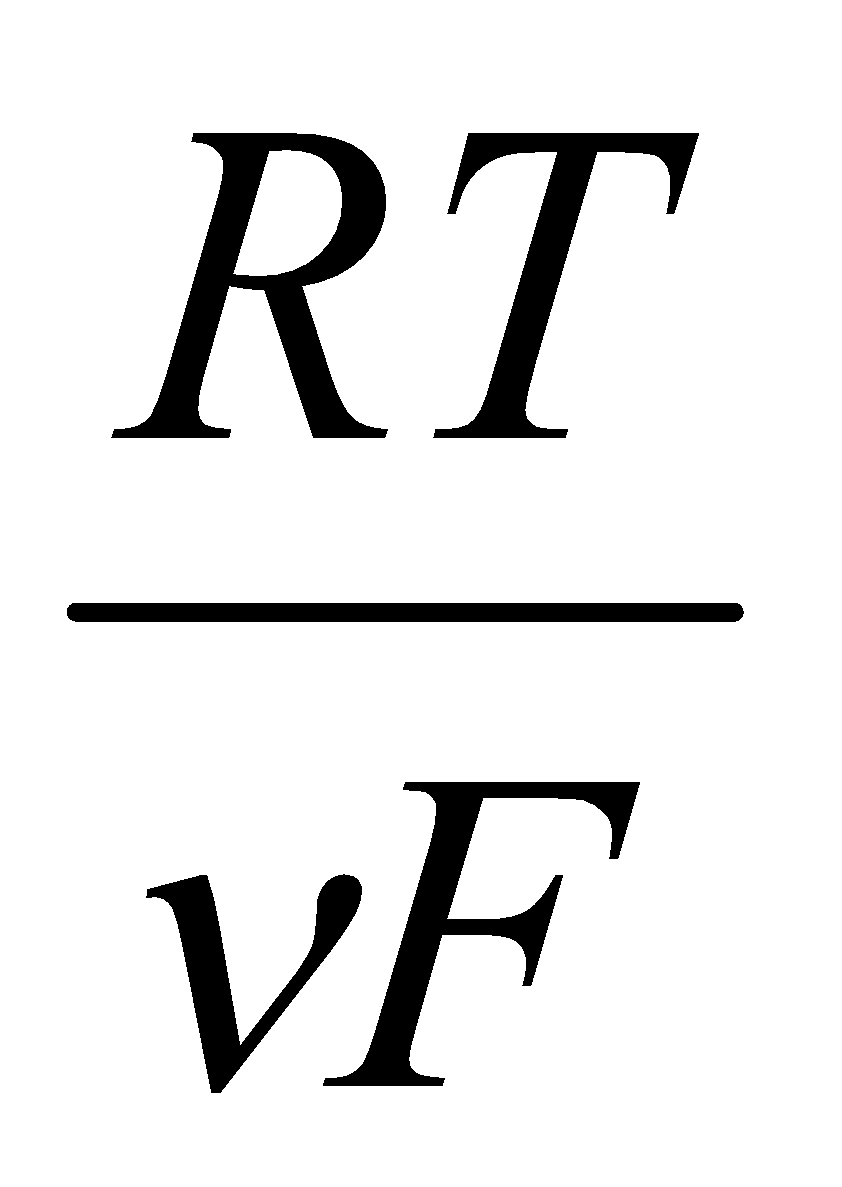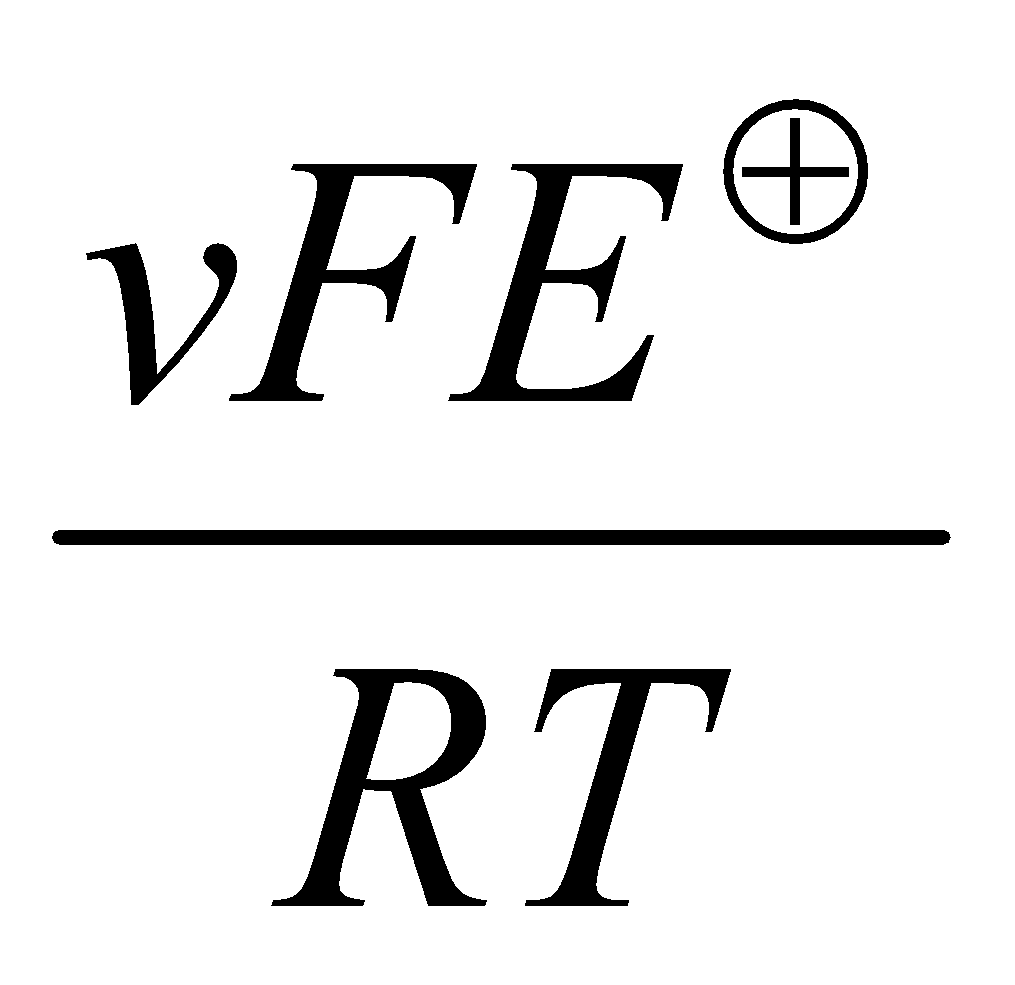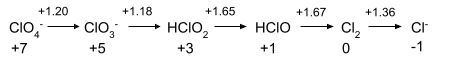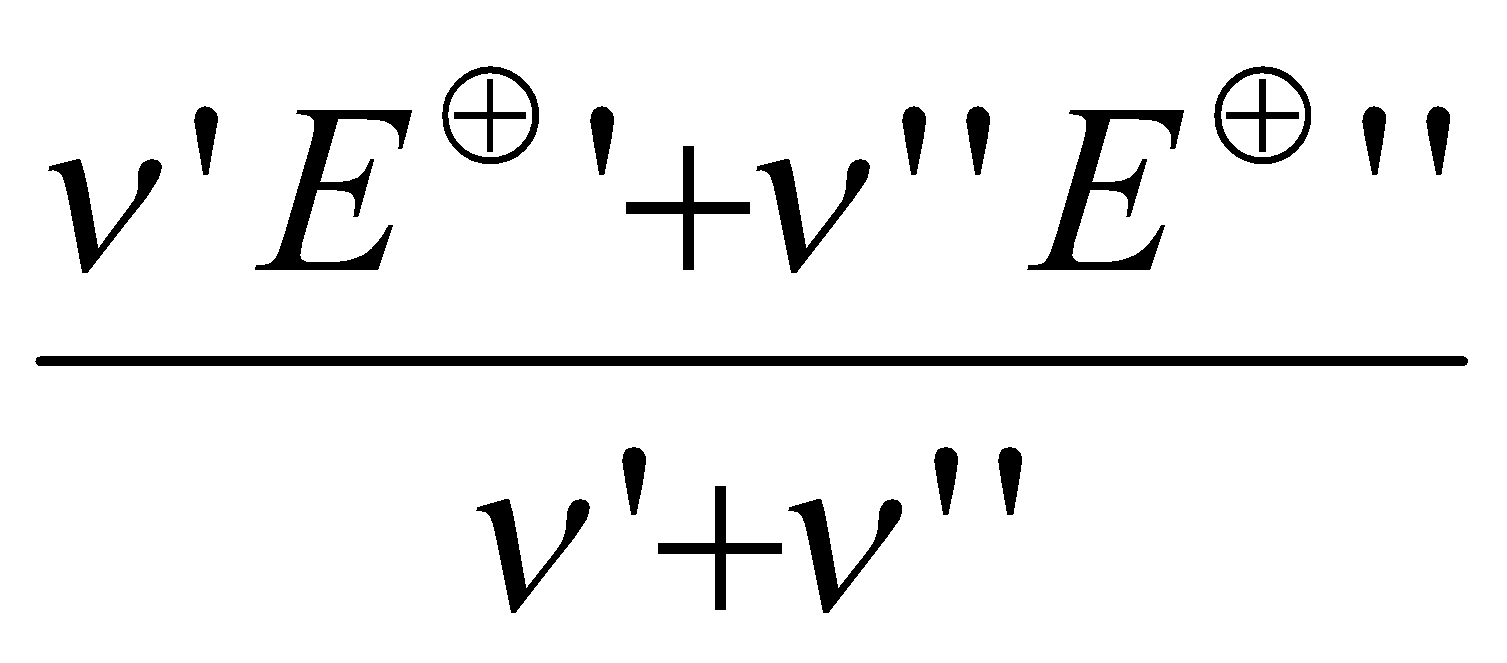Solutions and Redox
Some basic notes on Acids and Bases and Redox Reactions (Frost Diagrams, Pourbaix Diagrams, etc).
Solutions and Redox Notes
Acids and Bases
Bronsted and Lewis Acids and Bases
Bronsted – acids are proton donors, bases are proton acceptors.
Conjugate bases are weak when they are formed from a strong acid and vice versa. This is because the base has no inclination to regain a proton if it has a high tendency to lose it. Strong acid implies that the acid equilibrium lies largely to the right.
Lewis Acids – allows explanations of for example BF3, despite no H+. A Lewis Acid is defined as an electron pair acceptor. Associated with complex formation.
Hard & Soft –
Hard → small, polarising, hard to oxidise. e.g. Li+ (acid), F- (base)
Soft → large, polarisable, easy to oxidise. e.g. Ag+ (acid), I- (base).
pKa Values
Measure STRENGTH.
pKa = - log [Ka]
pH = - log [H+]
Thus, if its negative, then it’s a very strong acid. Equilibrium lies largely to the right, since Ka is more than 1.
A useful Ka is that of dissociation of water.
[H+][OH-] = 10-14
Thus, when conc. of an alkali is known, the pH can still be found.
Drago-Weyland Equation
A(g) + :B(g) → A-B (g) ΔrH (A—B)
ΔrH = EAEB + CACB.
Parameters: E stands for Electrostatic and C stands for Covalent. Thus, equation represents ionic and covalent contributions to complex bonds.
Pauling’s Rules
- OpE(OH)q → pKa 8 – 5p.
- Successive pKa values of polyprotic acids (q>1) increase by 5 units for each successive proton transfer.
This applies only to oxoacids, obviously. Thus, for OP(OH)3, pKa = 8-5(1) = 3. The value should be 2.1.
These rules can be useful for examining variations when they are wrong, such as with OC(OH)2, which has a pKa too low. This is actually due to the equilibrium of dissolved CO2 forming H2CO3. A similar and more extreme example is H2SO3, where OS(OH)2 apparently does not form.
Not all non-metal oxides react fully with water to form acids.
Irving-Williams Series
Ba2+> Sr2+> Ca2+> Mg2+> Mn2+> Fe2+> Co2+> Ni2+> Cu2+> Zn2+
Represents increasing stabilities from Ba to Zn, and is a measure of both increasing acidity and softness of the metal. See Transition Metal Notes for more detail.
Redox
Half-cell Reactions
2 half-reactions make up a redox reaction, one of which gains electrons and other loses them, e.g.
|
2H+(aq) + 2e- → H2 (g) |
Reduction |
|
Zn (s) → Zn2+(aq) + 2e- |
Oxidation |
Only part of a conceptual model, since the loss and gain of electrons cannot be separated into 2 separate process. However, as part of an electrochemical cell, the half-reactions can be partitioned so that the electrons are transferred between.
Standard Potentials
Since half-reactions always occur in pairs, the ΔG of each reaction is all that concerns us. Thus, a reference cell can be selected on which all other values are standardised. Thus, the potential for a Redox couple can be measured quantitatively relative to another couple in an Electrochemical Cell.
The reference reaction is that of Hydrogen above, and is given a value of ΔG = 0.
The potential difference is measured across the two cells (the reference cell being Hydrogen over Pt), and is related to the Gibbs Energy by ΔG = -νFE, where E is the standard electrode potential.
It is important that all reactions are set up as reductions, and then whether the E value is more positive or negative then determines whether it will be reduced or oxidised RELATIVE TO the reference cell. The more negative half-reaction is thus oxidised (reversed).
Using the equations above, E (Zn) = -0.76V. Thus, E for the reaction between Zn and H is +0.76V. H2 is reduced by Zn.
This shows a use of the Electrochemical Series – all E-values for Redox couples are arranged in order so that they can be compared. All independent of RATE. Shows spontaneity only.
Nernst Equation
Thermodynamically it can be shown that:
ΔrG = ΔrGo + RT ln Q
Can substitute for E and rearrange such that:
E = Eo + ln Q
This is the Nernst Equation. Eo is defined as a measurement of the potential difference produced between the electrode and the solution in question for the process Mn+1 + e- ⇌ Mn, relative to the standard hydrogen electrode (1 bar H2, [H+] = 1.0M at 298K), with the substances in their standard states and the potential difference taken at zero current.
At equilibrium, Q = K and E = 0, so:
ln K =
Example:
2Mn3+ + 2H2O ⇌ MnO2 + Mn2+
Mn3+ + e- ⇌ Mn2+ Eo = 1.51V
MnO2 + 4H+ ⇌ Mn2+ + 2H2O Eo = 0.95V
Eocell = Eo(Mn3+/Mn2+) – Eo(MnO2/Mn3+)
Eocell = 1.51 – 0.95 = +0.56V
Must be positive if the equation is the correct way round (can’t take log of a negative number).
Ecell = (RT/nF) ln K → ln K = 0.56/(8.314x298/F), and so K = 3x109.
Hence, 2Mn3+ → Mn2+ + Mn4+ is favourable (i.e. it disproportionates, see below).
Uses & Limitations
- Feasibility of reactions (thermodynamics only). Kinetics may prevent the reaction from occurring.
- Extent of the reaction (equilibrium constant).
- Solubility Products (not redox!). AB(s) ⇌ A+(aq) + B-(aq), and Ksp = [A][B].
- Thermodynamic quantities.
- Metal-Ligand effects, e.g. Fe3+(aq) Eo = 0.77V, Fe(CN)63- Eo = 0.3V, i.e. Fe3+(aq) is easier to reduce.
- Frost Diagrams, Pourbaix Diagrams, etc.
Overpotential
A negative standard potential for a metal-metal ion couple indicates that the metal can reduce H+ ions or any more positive couple under standard conditions in aqueous solution; it does not assure us that a mechanistic pathway exists for this reduction to be realised. There are no fully general rules that predict when reactions are likely to be fast. However, a useful rule-of-thumb (but with notable exceptions) is that couples with potentials that are lower than the hydrogen potential (at the prevailing pH) by more than about 0.6V bring about the reduction of hydrogen ions to H2 at a significant rate. Similarly, potentials that are higher than the potential of the couple O2,H+/H2O at the prevailing pH by more than about 0.6V can bring about the oxidation of water.
The additional potential of 0.6V is an example of overpotential, the potential beyond the zero-current (“equilibrium”) potential that must exist before the reaction proceeds at a significant rate. The existence of overpotential explains why some metals reduce acids but not water itself. Such metals (e.g. iron and zinc) have negative standard potentials, but these potentials are not low enough to achieve the necessary overpotential for the reduction of H+ in neutral solution. However, the difference of E(H+,H2) – E(Fe2+,Fe) can be increased if E(H+,H2) is made more positive, which can be done by lowering the pH. When the difference exceeds about 0.6V, the metal brings about reduction at an appreciable rate.
Latimer Diagrams
Latimer Diagrams are good for summarizing quantitative data element by element.
Standard Electrode Potentials written over line, oxidation state underneath, beginning with the most highly oxidised form on the left.
Chlorine in Acid:
To write out each step requires balancing of half-reaction, usually involving H+ and water.
Non-adjacent species can be related by looking at the change in E-values over several steps. Since, ΔG = ΔG’ + ΔG’’
By rearrangement,
E =
Disproportionation:
2M+(aq) → M(s) + M2+(aq).
Can be expressed as:
|
M+ + e → M |
R |
|
M2+ + e → M+ |
L |
Where R/L stands for right/left in a Latimer diagram. E cell is positive for spontaneous change, and E(std) = E(R) – E(L). Thus, a species has a thermodynamic tendency to disproportionate when the potential on the right of the species is higher than the potential on the left.
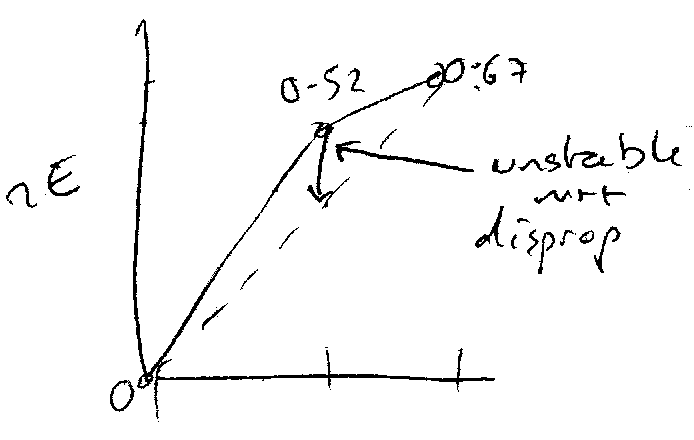
Frost Diagrams
Frost Diagrams are useful for qualitative portrayal of the relative stabilities of oxidation states. They are a plot of nE against N (where N is oxidation number).
Lowest points are most stable.
This is relevant for disproportionation, particularly. When one of the points is above the line connecting 2 adjacent species, then disproportionation will occur.
Similarly, comproportionation can be indicated by a point being lower than the line joining adjacent species, such that the 2 higher species comproportionate. This is because the mean Gibbs Energy is lower in the lowered state.
Steep graph = higher potential (gradient = standard potential). This is useful for comparing couples. Steeper line → more likely to undergo reduction.
Hence, for a negative gradient, +ΔG → oxidising. For a positive gradient, -ΔG (reducing), e.g. MnO4- strong oxidising agent (steep positive line between it and MnO2).
Some Examples:
0.15 0.52
Cu2+ Cu+ Cu
+2 +1 0
Cu+ + e- ⇌ Cu Eo = 0.52V
Cu2+ + e- ⇌ Cu+ Eo = 0.15V
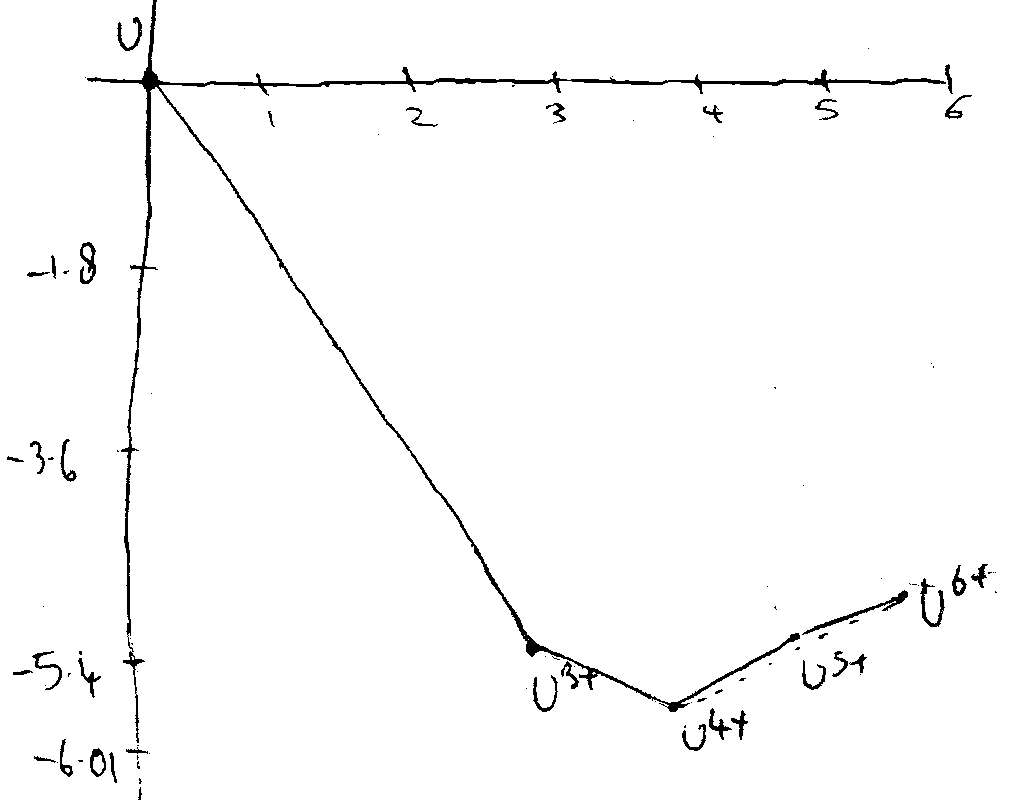
0.05 0.062 -0.61 -1.3
UO22+ UO2+ U4+ U3+ U
+6 +5 +4 +3 0
Non-adjacent couples: e.g.
UO2+/U → [ (1)0.62 + (1)(-0.61)+(3)(-1.8) ] / 5
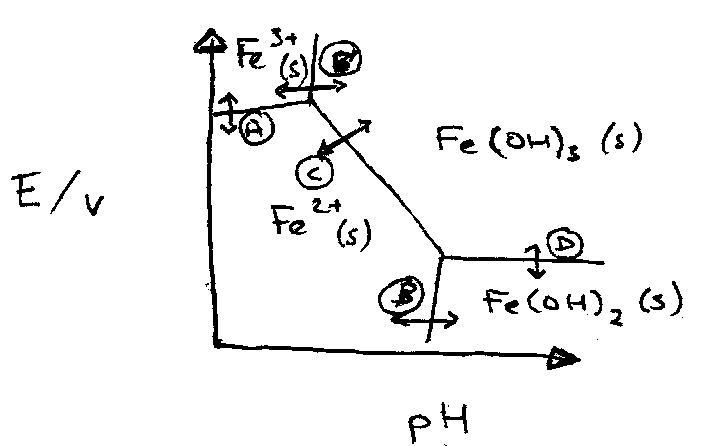
Pourbaix Diagrams
Links Bronsted Acids to Redox. pH Dependence of Redox processes –
E = Eo + (RT/nF) ln Q
H+ + e- = ½ H2, Eo = 0.
E = 0 – (RT/nF) ln ( 1/[H+] )
E = -0.059 (pH)
Thus, any redox equilibrium which has protons in it depends on pH, as the concentration of [H+] affects the equilibrium.
For example, PuO2+ + e- + 4H+ = Pu4+ + 2H2O
Acid conditions drive this, but not basic. Basic → H2O → -OH. More oxidising in acid. Protons “mop up” oxide.
This can be explained qualitatively using Le Chatelier’s Principle.
A Pourbaix Diagram is essentially a map of Potentials vs. pH in water. How E-values vary as a function of pH.
At A: Redox independent of pH. Straight line. No H+ in Q of the Nernst Equation.
Fe3+ + e- → Fe2+
At B and B’: pH dependent, but not a redox process.
Fe3+ + 3H2O ⇌ Fe(OH)3 + 3H+
At C: E is pH dependent. Diagonal.
Fe(OH)3 + e- + 3H+ ⇌ Fe2+ + 3H2O
E = Eo - ln ( 1/[H+] ), implies as [H+] drops, therefore E increases.
Gradient → which side of the equation H+ is on.
At D: an order of H+ lower (only 1 x H+).
I am happy for them to be reproduced, but please include credit to this website if you're putting them somewhere public please!