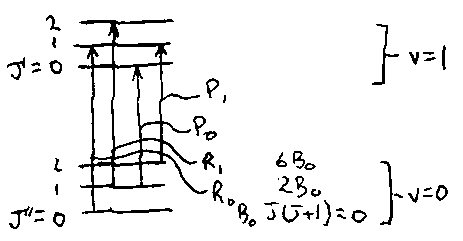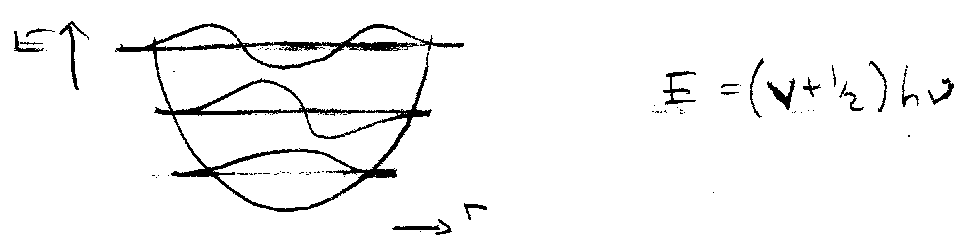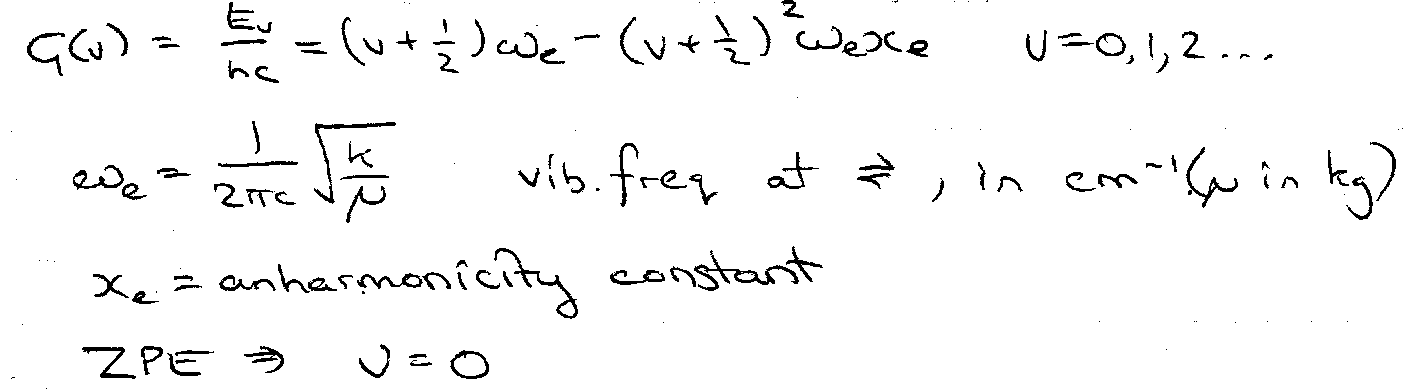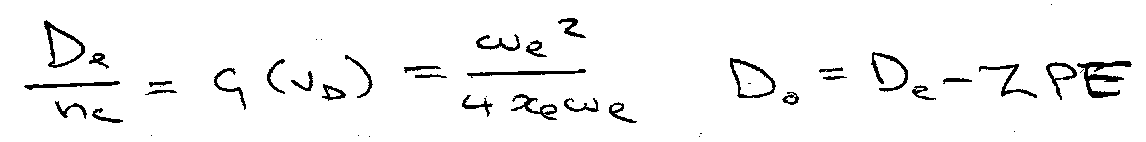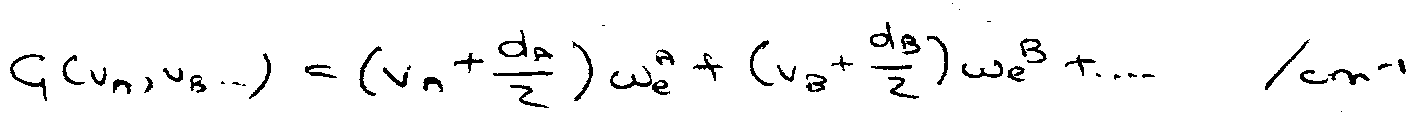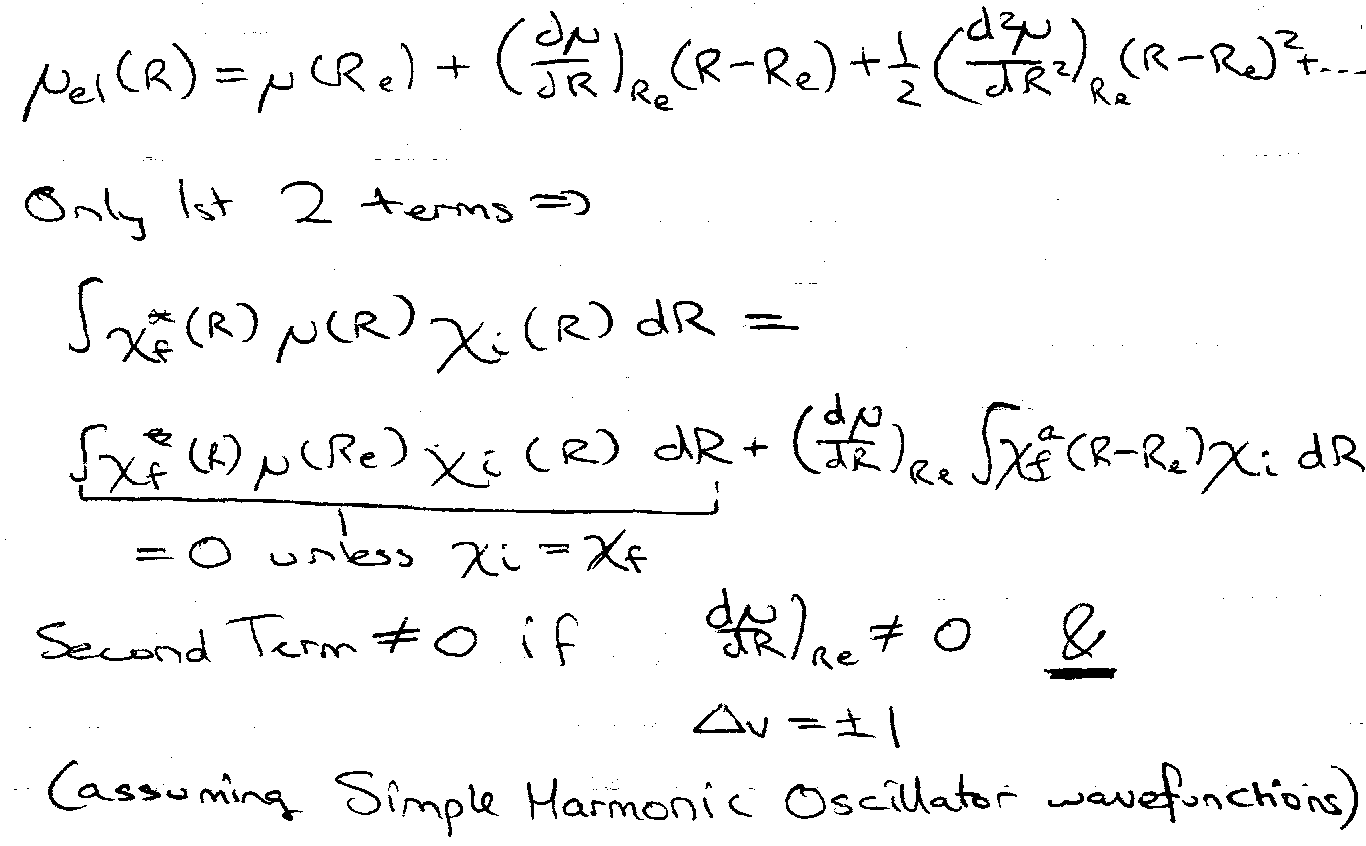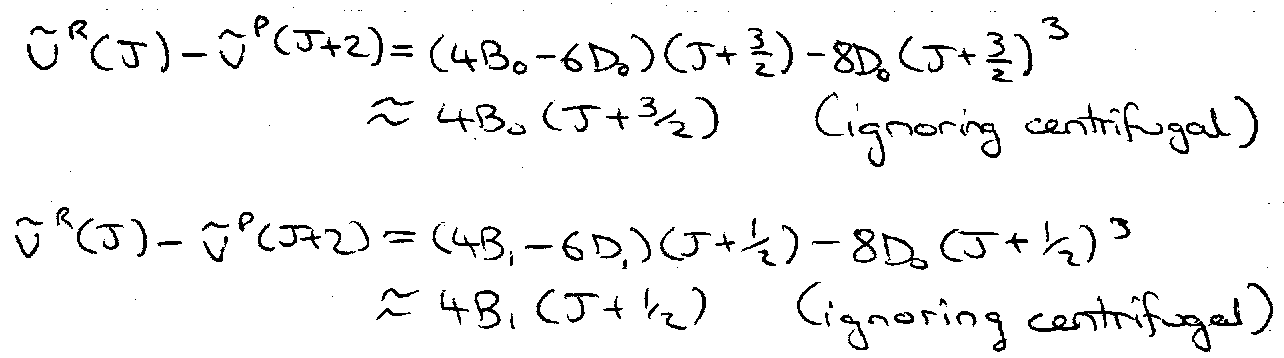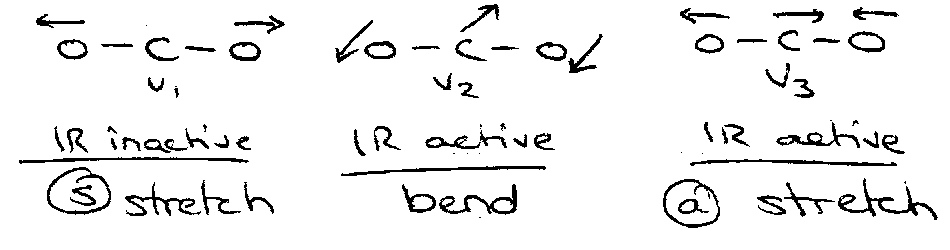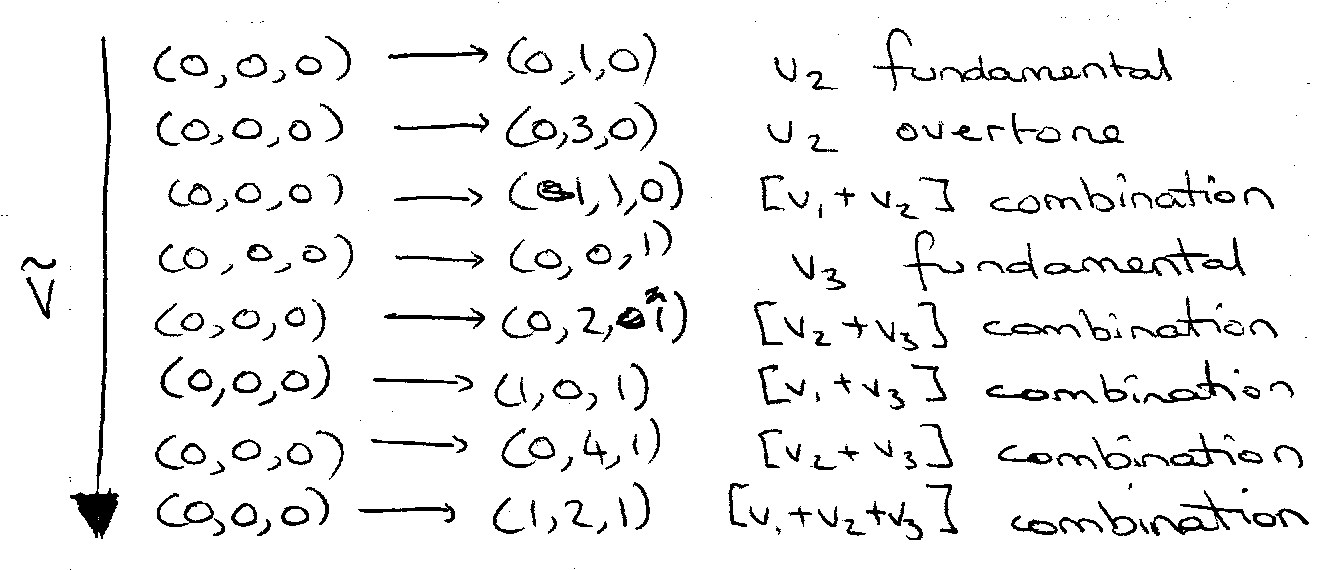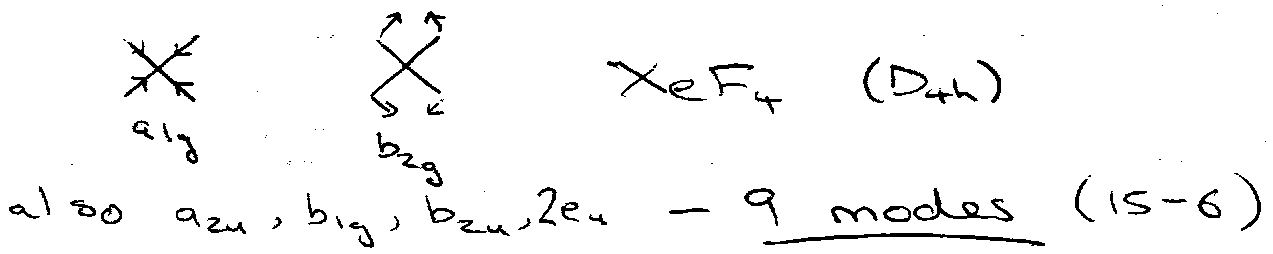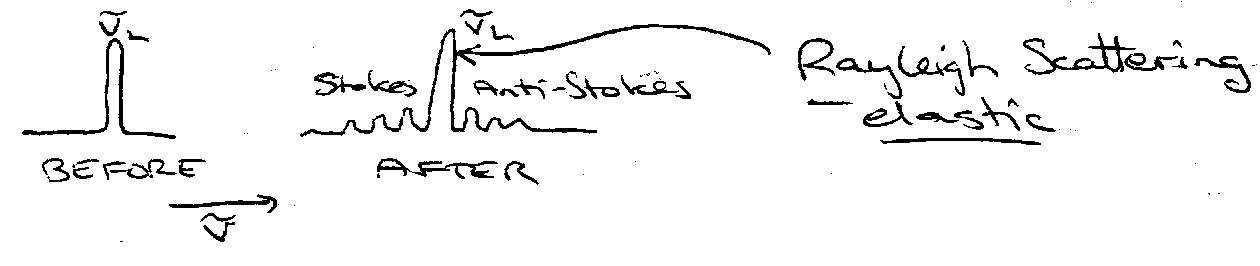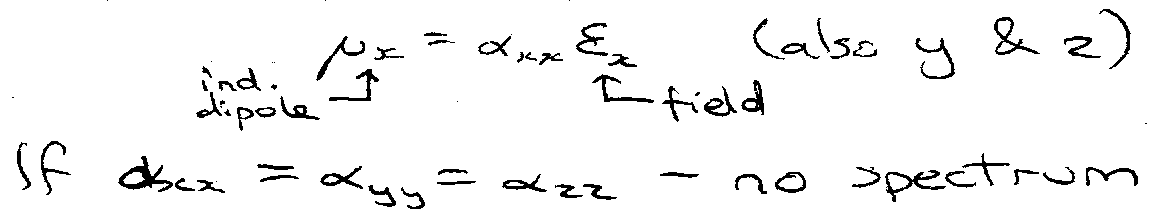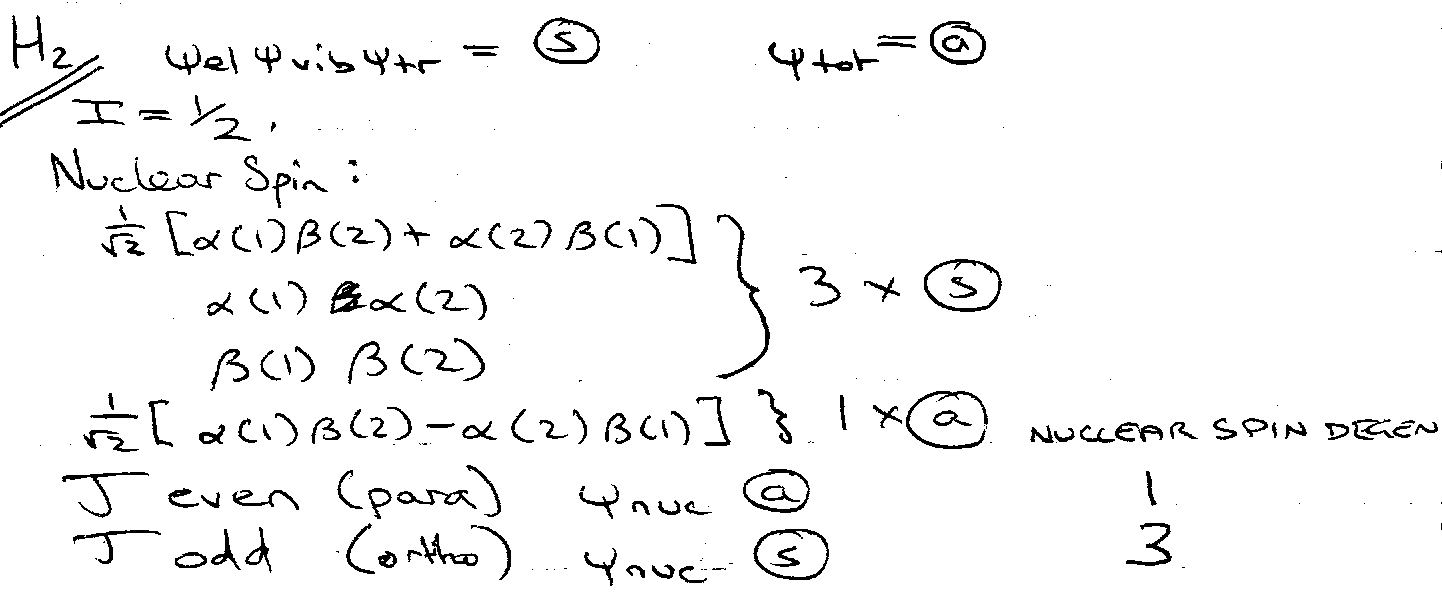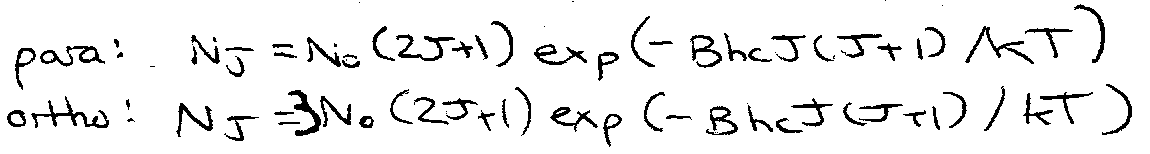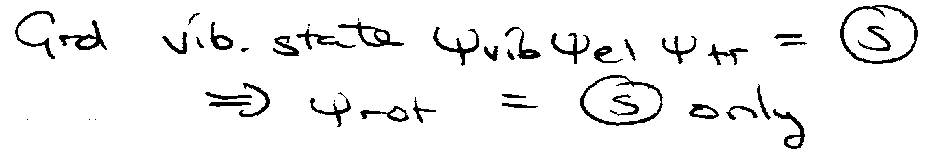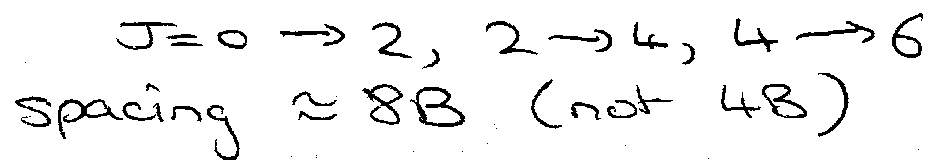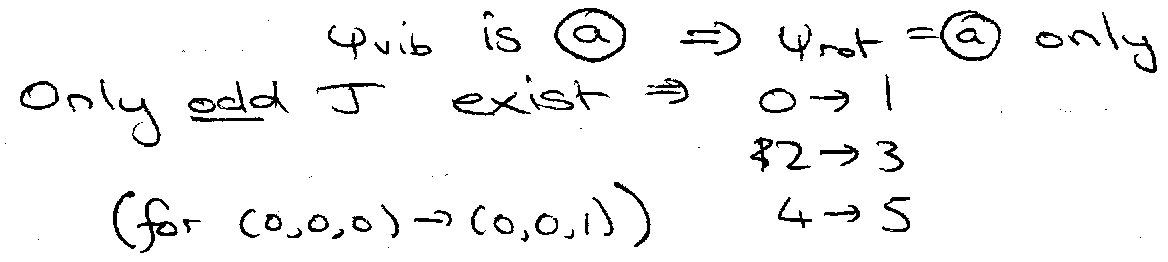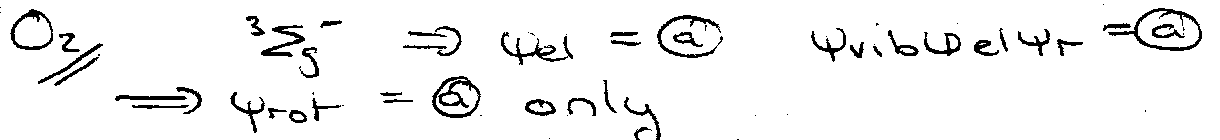Vibration-Rotation Spectra

SUMMARY

Every vibrational energy level has a rotational energy level structure built on it. The rotational part is exactly as in the previous section, but centrifugal distortion can be ignored. For one vibration (e.g. a diatomic), energies G(v) are expressed as:

G(v) = (v+½)ωe – (v+½)2ωexe + (possible higher terms)

A simple harmonic oscillator (SHO) has only the first term. ωe and ωexe are the frequency and anharmonicity for infinitesimal vibration amplitude at the bottom of the potential well.

Selection Rules:

1. For IR, the vibration must cause a change in dipole moment.
2. For Raman, the vibration must change the polarisability.
3. In centro-symmetric molecules, no vibration can be both IR and Raman active.
4. In both IR and Raman, Δv = ±1 transitions are by far the strongest. This rule is not strict, because:

1. a transition dipole can come from higher powers of the vibration coordinate extension, even for SHO.
2. Anharmonicity removes the symmetry of the vibration wavefunctions. So Δv = ±2, ±3… transitions are seen weakly.

5. The selection rules for rotational fine structure are ΔJ = ±1 for IR and ΔJ = 0, ±2 for Raman, if no other angular momentum is present. If another angular momentum is present then  ΔJ = 0,±1 for IR and  ΔJ = 0, ±1, ±2 for Raman.

Line Positions:

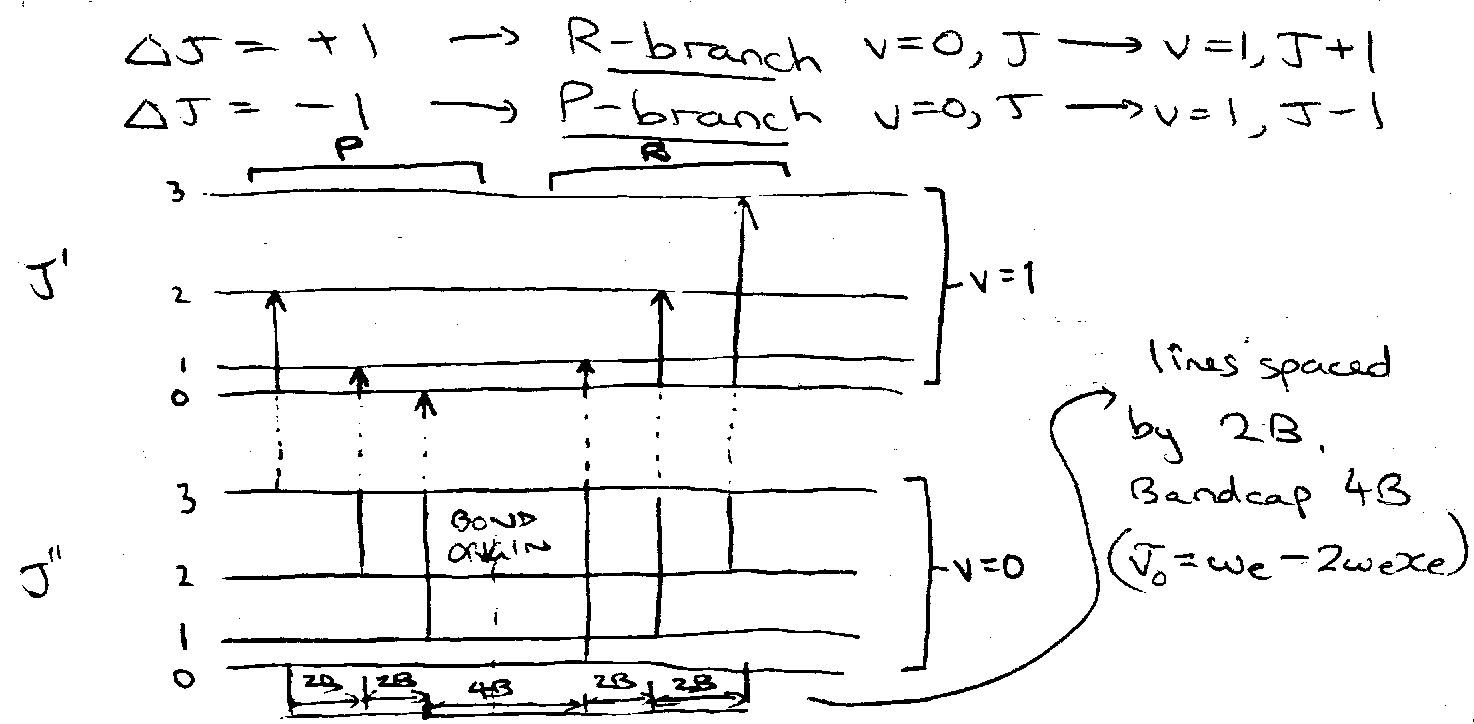
For Δv = 1, the vibrational origins (ΔJ = 0) are at ΔG(v) = ωe – 2vωexe, where v is the quantum number of the upper state. Successive origins differ by 2ωexe.

IR rotational structure may have P,Q and R branches for ΔJ = -1,0,+1 respectively. The B values are different in each vibrational level, written B0, B1, etc. Because they are only slightly different, the P and R branches have a line spacing of about 2Bav, but there is a double-sized gap of about 4Bav at the band origin. Lines close up in the R branch and spread out in P.

Remember that when observing different isotopes (e.g. HCl), the correct ratio (for this example it would be 3:1) is NOT seen, because transmittance is on a logarithmic scale.

The B values are smaller for higher vibration levels, because on average the bonds get extended:

Bv = Be – (v+½)α

From B values in two levels α can be found (B1 – B0 = α). Be is the (theoretical) rotational constant at the bottom of the potential well and gives the equilibrium bond length.

Formally, Be = h/(8π2cI) where I = μre2.

For Raman, with ΔJ = 0, ±2, the structure is analogous.

Intensities:

For the rotational part, populations are as given in the last section. Vibrational energies are >kT, so normally only v=0 is strongly populated. The weak transitions starting from v=1 etc. are called hot bands.

Vibrational Energy Levels

Energy of a molecular vibration depends on internuclear distance.

Harmonic Oscillator + Quantum Mechanics gives:

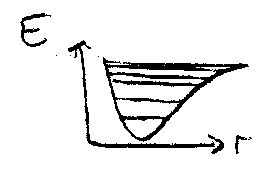
A real diatomic curve diverges at higher energies:

This is anharmonicity. Convergence of energy levels. This is described well by:

E = (v+½)hν – (v+½)2xeν + (v+½)3yehν

xe – small anharmonicity correction term. Further terms are even smaller, usually neglected.

Isotopically related molecules (e.g. H2 and D2) have identical potential energy curves. Independent of mass. k is thus the same, so can predict energy level spacings. Spacing smaller for the heavier isotopes.

Dissociation Energies are thus different → smaller ZPE for heavier atoms. C-H easier to break than C-D.

Diatomics:

Harmonic Oscillator Potential:

V(R) = ½ k (R – Re)2.

Morse Potential:

V(R) = D [ 1 – ea(R-Re) ] 2

a = 2πcωe(μ/2De)1/2.

Dissociation Energy:

dG(v) / dv = 0 at v = 0

Polyatomics:

Quanta in normal modes – A,B,C … : vA, vB, vC …

Degeneracy dA, dB, dC…

Ignoring Anharmonicity:

No simple relationship between bond force constants and vibrational frequencies of normal modes.

Vibration-Rotation Energy Levels

Diatomics:

F(v,J) = G(v) + F(J)

B varies with vibrational level as:

Bv = Be - α (v+½).

Be = h/8π2cμre2

Symmetric Top  Polyatomics –

F(vA, vB …; J; K) = G(vA, vB, …) + F(J,K)

Bv = h/8π2cμ(<1/r2>v)

Variation due to:

• Anharmonicity
• Intrinsic property of <1/r2>

Infrared Spectroscopy – Vibration-Rotation

Diatomics –

Vibrational Changes:

For real molecules, anharmonicity → Δv = ±2, ±3 …

Allowed, but weak.

Also, dipole moment change ≠ 0, so heteronuclear only.

Populations –

Nv/No = e-G(v) hc / kT

Hence for most diatomics, only see absorption from v = 0 (for room-temp).

Vibrational Transition Energies –

G(v+1) – G(v) = ωe – 2(v+1) ωexe.

For v =0, = ωe - 2ωexe ≈ vo

This vo is the Fundamental vibrational frequency.

First Overtone, G(2) – G(0) = 2ωe – 6ωexe.

Note, De = ωe2/4ωexe

Rotational Changes – ΔJ = ±1

R-branch:

vR(J) = F(v+1,J+1) – F(v,J) = vo + (Bo+B1)(J+1) + (B1-Bo)(J+1)2

P-branch:

vP(J) = F(v+1,J-1) – F(v,J) = vo – (B1+Bo)J + (B1-Bo)J2

v(J+1) – vP(J) = - (B1+Bo) + (B1-Bo)(2J+1)

Isotope Effects –

ωe 1/√μ

ωexe1/μ

Be 1/μ

Combination Differences –

In IR vib-rot spectra.

Normal Modes in polyatomic molecules. Combined motion of several atoms.

Bond vibrations not independent.

What are Normal Modes?

The vibratory motions in a polyatomic molecule can be analysed as a sum of “normal modes”, component vibrations in which all atoms move at the same frequency with sinusoidal displacements.

Normal modes are SHO, independent, and orthogonal – model valid for low quantum numbers only.

N – number of atoms:

Displacement in MASS-WEIGHTED sum of coordinates Qi such that all terms of the form d2V/dQidQj = 0

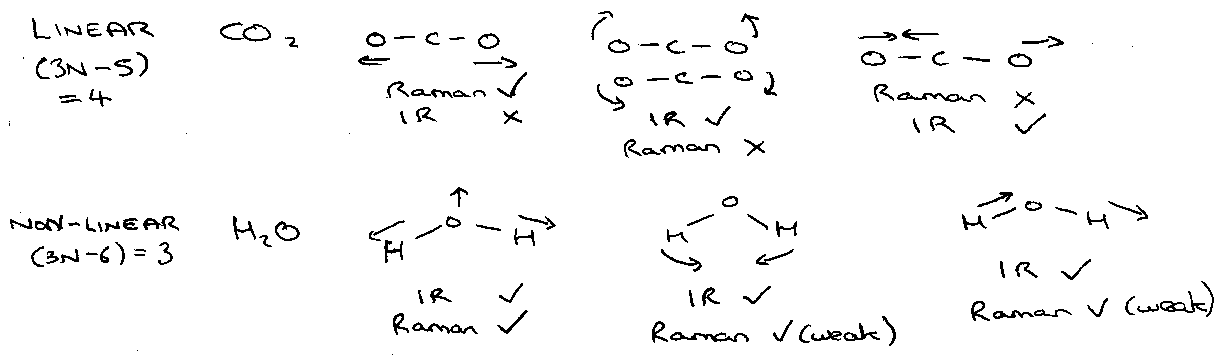
Linear –

3N – 5 normal modes of vibration.

e.g. CO2:

G(v1, v2, v3) = (v1+½)ω1 + (v2+½)ω2 + (v3+½)ω3

(ignoring anharmonicity)

Infrared Selection Rules –

Dipole moment must change on vibration.

ΔJ = ±1 for parallel vibrations (change parallel to linear molecule xis).

ΔJ = 0, ±1 for perpendicular vibrations (change perpendicular to axis – bending).

Q-branch –

G(v2=1, J) – G(v2=0, J) = (B1-Bo)J(J+1) + vo.

B1 – Bo small – transitions pile up.

Transition allowed because of double degeneracy.

Symmetry of Rotational Wavefunction – parity.

Designate levels wrt space-fixed inversion.

+ ↔ -                         -         allowed

+ ↔ + / - ↔ -                 -         disallowed

Overtone and Combination Bands (Linear)

Overtone – change of vibrational quantum number by > 1 in one mode.

Combination Band – excitation of 2 different vibrational modes simultaneously.

Example, CO2

Selection Rules for Overtones and Combinations:

v1 – g symmetry.

v2 – u for odd quanta, g for even.

v3 – u for odd, g for even.

(0,0,0) – g.

Selection Rule – g ↔ u.

Vibrational Spectroscopy of Non-Linear Polyatomics

3N – 6 normal modes of vibration.

Characterise by irreducible representations of the molecular symmetry group, e.g.

Those displayed above → no dipole change. IR inactive.

Vibrational Selection Rules:

< ψi | μ | ψf > - totally symmetric.

→ must contain A1 for allowed transition.

Γμ - transforms as x, y, z.

ΓχI – normally totally symmetric for Ground Level (a1g).

Γχf – must transform as x, y or z.

For D4h, a2u and eu modes active (those with x, y, z in character table).

Rotational Structure in IR Spectra of Polyatomics – Symmetric Top

Selection Rules:

Parallel (allowed by z) –

ΔK = 0

ΔJ = ±1 for K = 0, ΔJ = 0, ±1 for K ≠ 0

.

Perpendicular (allowed by x,y) –

ΔK = ±1

ΔJ = 0, ±1

Overtones and Combination Bands (Polyatomics)

Consider direct product for excited modes. Overtone allowed if product transforms as x,y,z.

e.g. D4h – b1g x b2u = a2u (allowed).

Hot Bands

Intensity of transitions from vibrationally excited states increases as T increases.

Group Frequencies

Bond vibrations strongly coupled if similar intrinsic frequencies. Some bonds almost completely decoupled → Group Frequency.

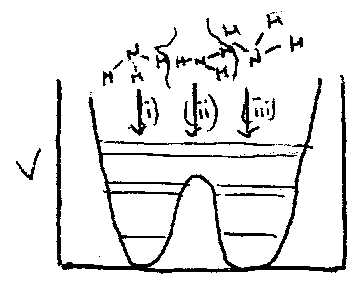
Tunnelling and Inversion

When more than one minimum in PE surface → overlap of vibrational wavefunctions possible → tunnelling, e.g. NH3:

± linear combinations have slightly different energies.

Overlap increases nearer top of the well, hence tunnelling splitting increases.

Tunnelling Splitting Frequency = rate constant for inversion.

Small splittings in other bands also observed due to anharmonic effects, e.g. excitation of other vi stretching mode causes slight change in bonding potential – different tunnelling frequency.

Broadening in Spectra

1. Lifetime broadening – “natural linewidth”.
2. Pressure broadening (collisions)
3. Doppler Effect (effective frequency observed by molecule)
4. Power (saturation) broadening.
5. Unresolved underlying structure.
6. Instrumental resolution.

Lifetime Broadening – if the probability of a system existing in a particular state decays as:

| ψ | 2 = | ψ |2 e –t/τ

This gives rise to an energy uncertainty.

τ δE ≈ h.

δE is the full width at half maximum height.

τ δv = 1/2πc

Raman Spectroscopy

Monochromatic light, wavenumber vL (visible).

Measure spectrum of scattered light.

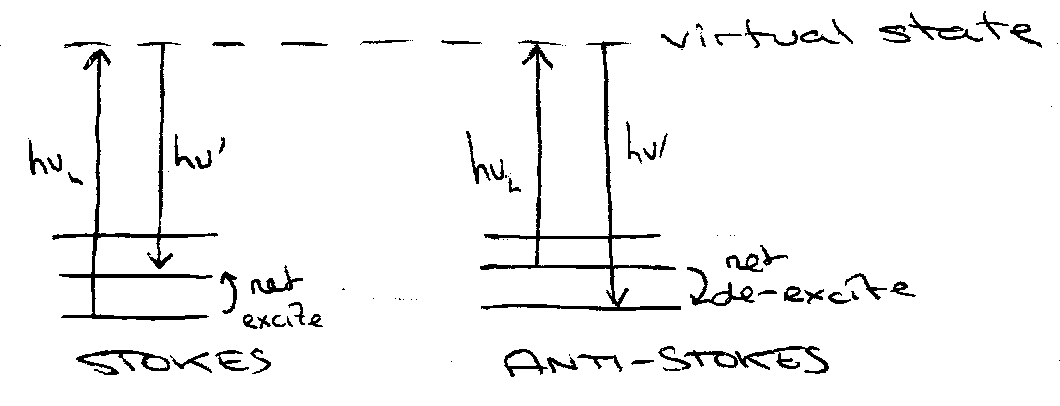
Raman Effect. Inelastic Scattering:

• v’ > vL – Anti-Stokes
• v’ < vL – Stokes

Conservation of Energy: hv’ – hvL = ΔE.

Quantum Picture of Raman –

The “absorption” and “emission” are instantaneous and simultaneous – no transfer of population. “virtual” state – off-resonant, transient, polarisation induced.

Both pure rotational and vib-rot changes are observed:

Classical description of Raman –

Molecule rotating at frequency ω’ – polarisability oscillates with frequency 2ω’ → oscillating dipole radiates.

Gross Selection Rules for Raman:

Rotational – molecule must have anisotropic polarisability.

Generally only true for Spherical Top – Ia = Ib = Ic.

Vibrational – polarisability change on vibration.

Selection Rules –

ΔJ = 0, ±2 (rotational and vibrational)

Rotational –

ΔJ = 0 (Rayleigh)

ΔJ = ±2 Stokes / Anti-Stokes

F(J+2) – F(J) = B[(J+2)(J+3) – J(J+1) ] = (4J+6)B

So Stokes lines at vL – (4J+6)B                        J = 0,1, …

F(J-2) – F(J) = (4J-2)B

So Anti-Stokes lines at vL + (4J-2)B                J = 2,3, …

Resolution is not normally sufficiently high to include centrifugal distortion.

Vibrational Raman

Rotational Structure –

Q-branch: Δv = 1, ΔJ = 0

F(v=1,J) – F(v=0,J)                [ displacement from vL ]

= vo + (B1 – Bo)J(J+1) ≈ vo [ = ωe – 2ωexe ]

S-branch: Δv = 1, ΔJ = +2

F(v=1,J+2) – F(v=0, J)

= vo + B1(J+2)(J+3) – BoJ(J+1)

= vo + (B1+Bo)(2J+3) + (B1-Bo)(J2 + 3J + 3)

O-branch: Δv = 1, ΔJ = -2

F(v=1,J-2) – F(v=0, J)

= vo + B1(J-1)(J-2) – BoJ(J+1)

= vo – (B1+Bo)(2J-1) +(B1-Bo)(J2 – J + 1)

Rule of Mutual Exclusion – Polyatomic

For molecules with centre of inversion symmetry (i); IR active modes are Raman inactive and vice versa. There may be some modes that are inactive in both.

Transition Intensities and Group Theory

Raman effect arises from interaction of the induced dipole moment of the molecule with the EM field.

For a diatomic in an E-field ε polarised in the z-direction, the component of the induced dipole in that direction:

2 parts of μz transform in D∞h group in the same way as x2 + y2 and z2 (A1g).

Transition Moment (Raman) is of the form:

< v’J’ | μz | v’’J’’ >

For non-zero transition probability require:

Γv’, Γμ, Γv’’ transforms to A1g (totally symmetric)

x2, y2, xy etc → g

x, y, z → u

(Hence mutual exclusion principle above).

Effects of Nuclear Spin Statistics

Pauli Principle:

Can thus stipulate symmetric of ψnuc.

Applications to Diatomics (homonuclear) and Linear Molecules

Populations

Raman of H2 – there is a 3:1 intensity alternation, in favour of the odd J lines.

CO2 – exchange of 16O I = 0 ψtot = symmetric.

ψnuc can only be symmetric.

For rotational Raman:

Only even J levels exist, so observe transitions:

For infrared: for (0,0,1).

Only odd J levels exist. Raman: 1 → 3, 3 → 5, …