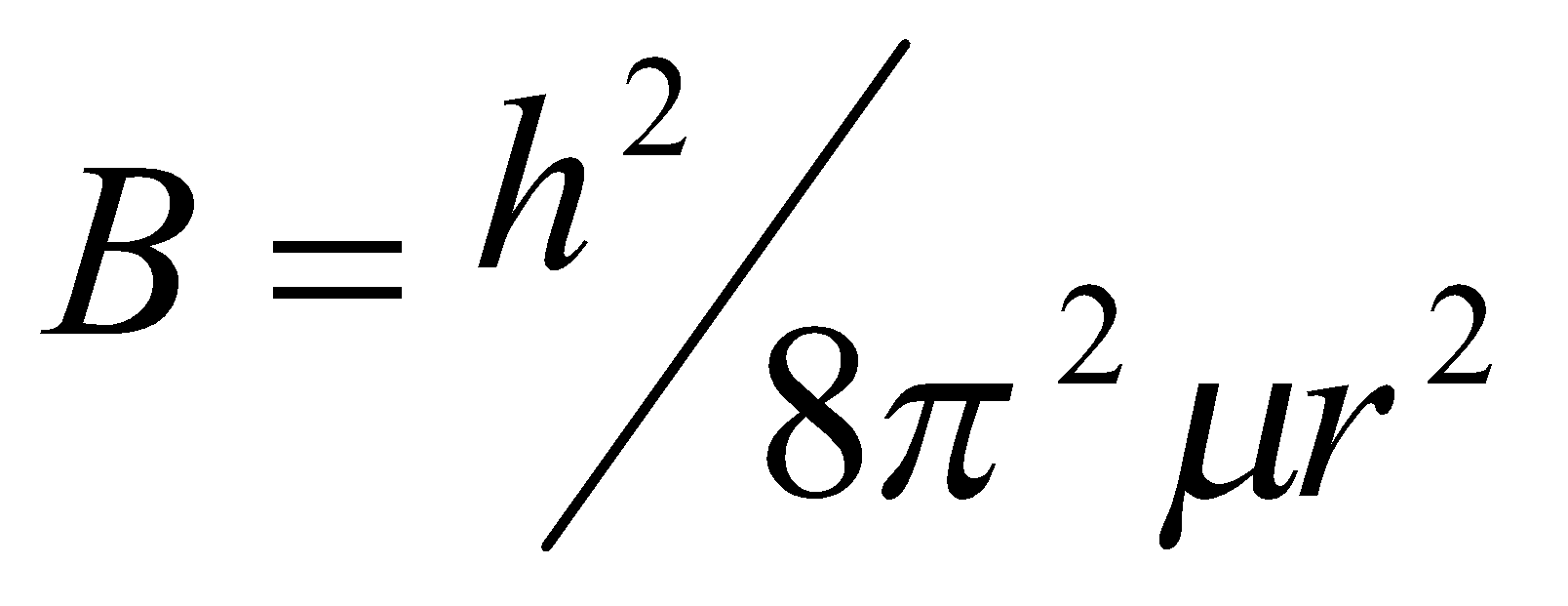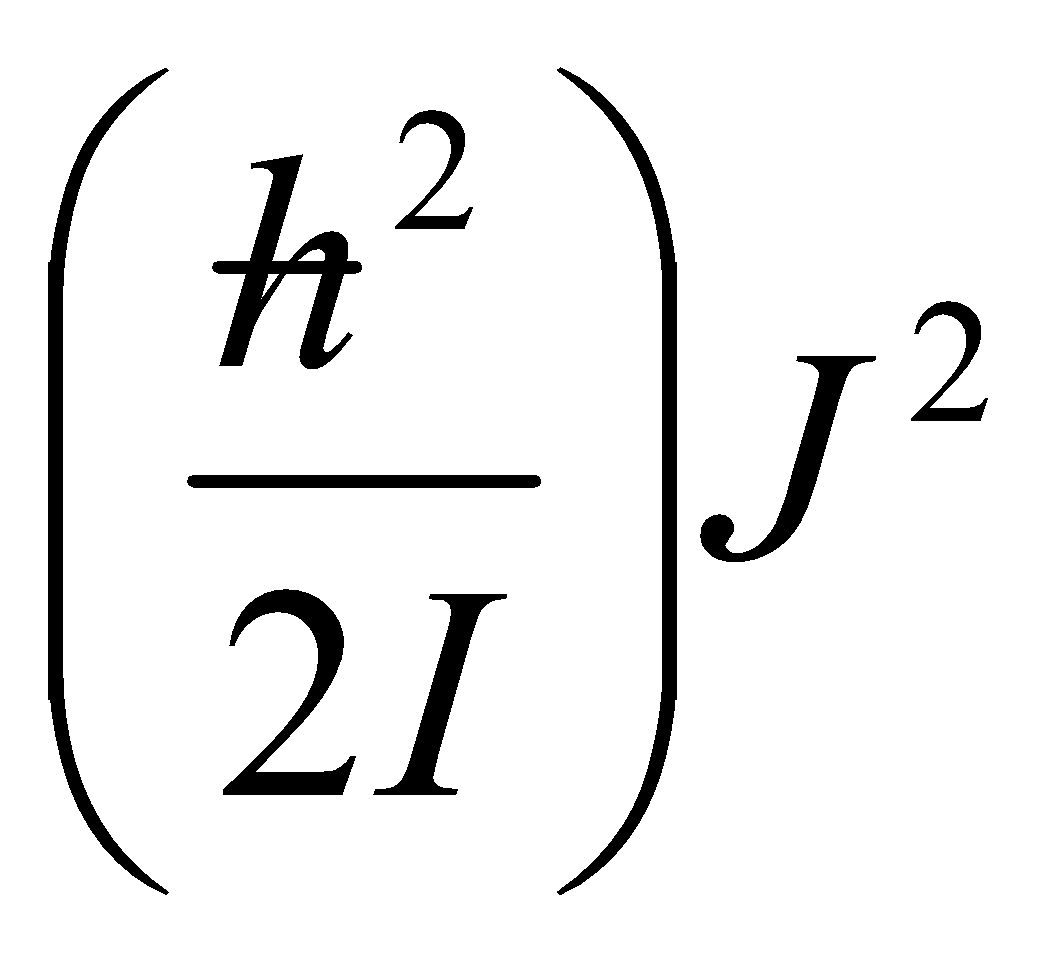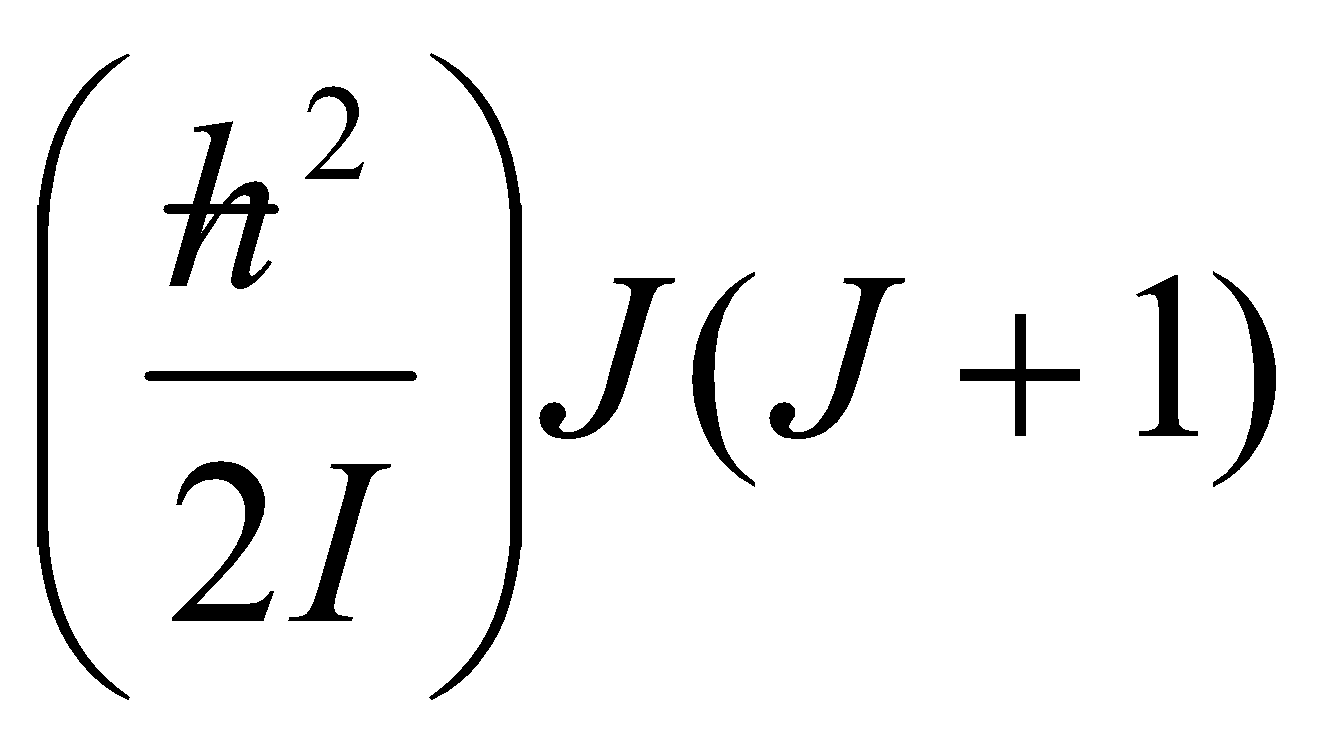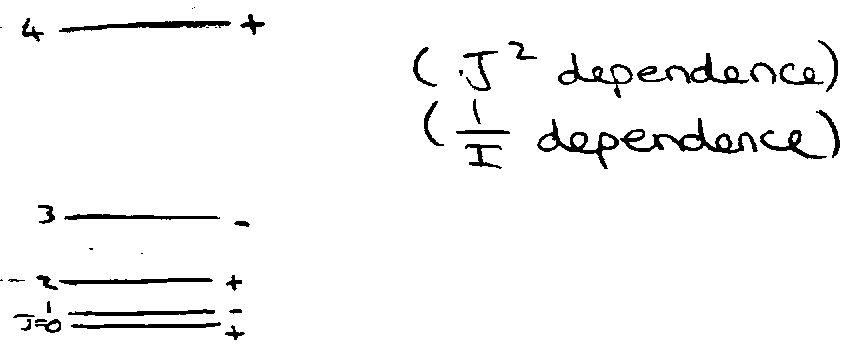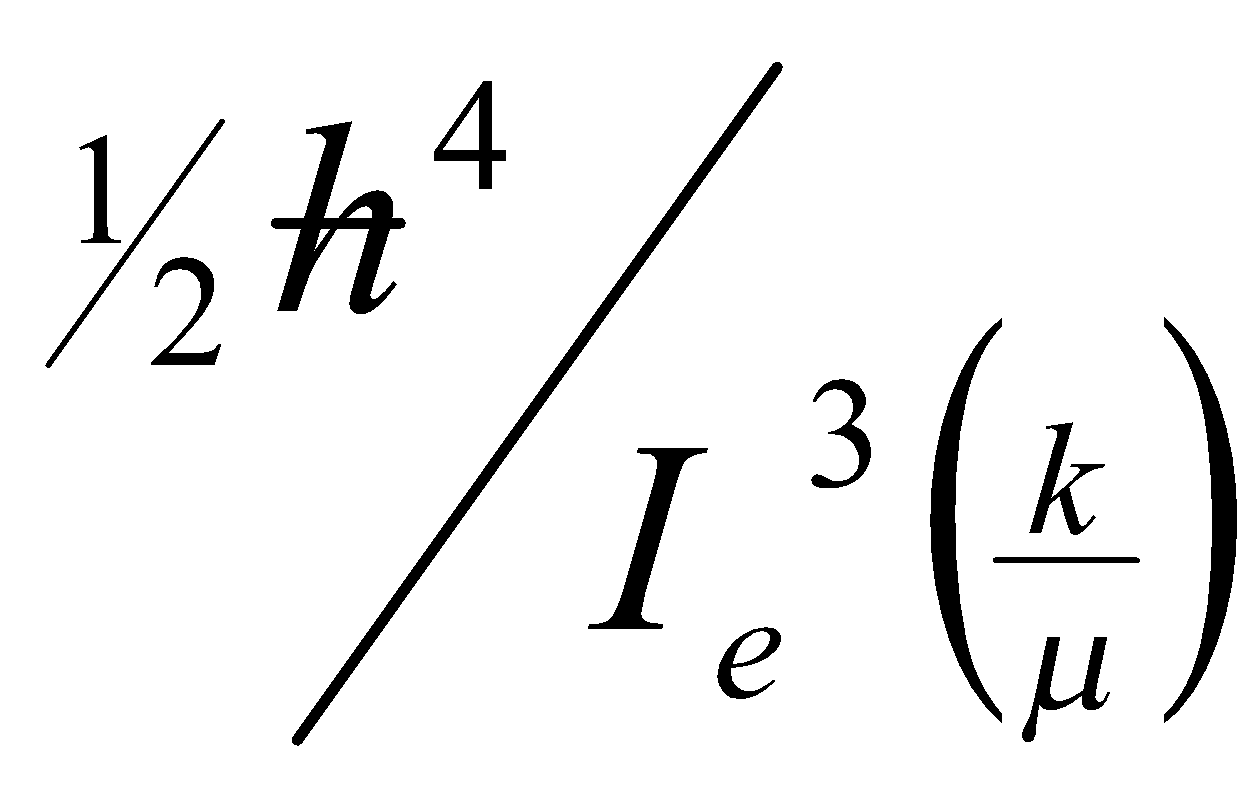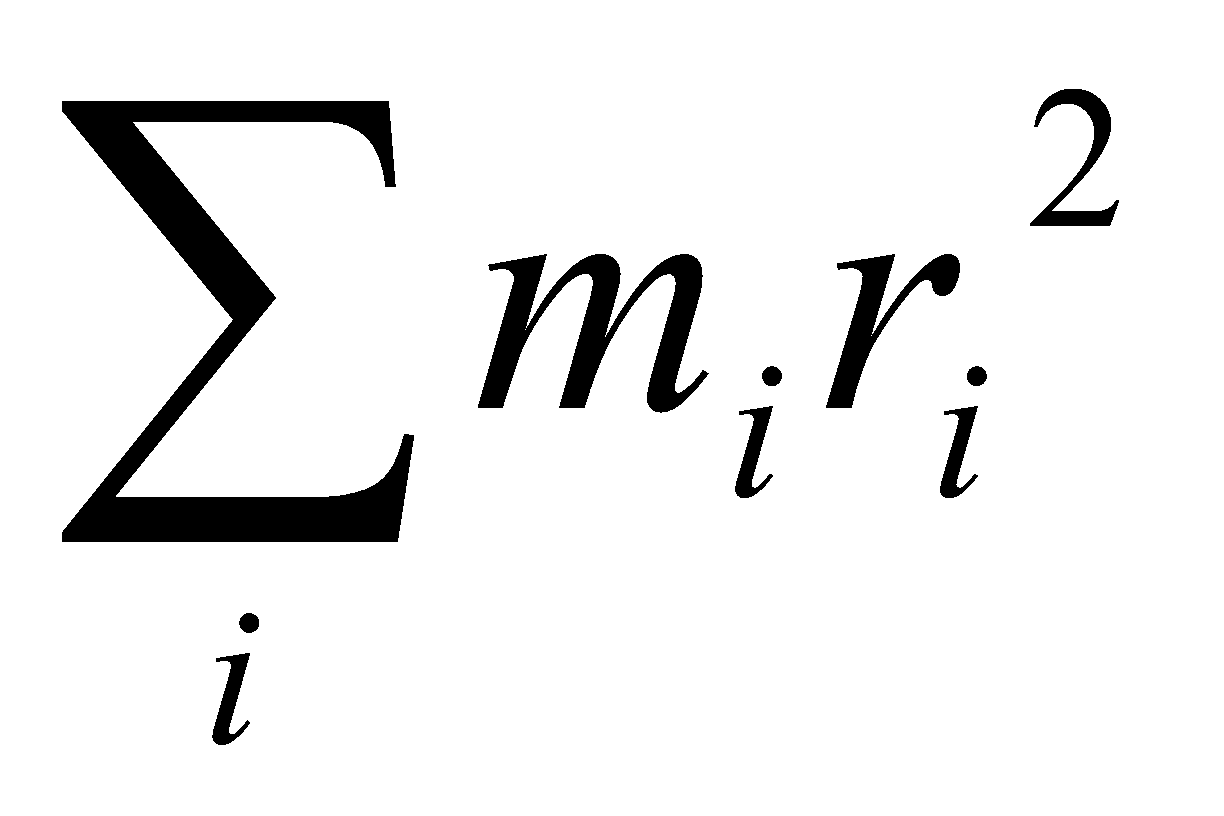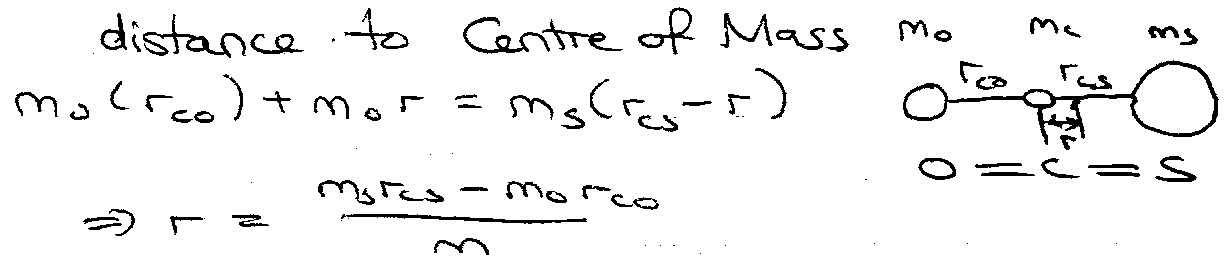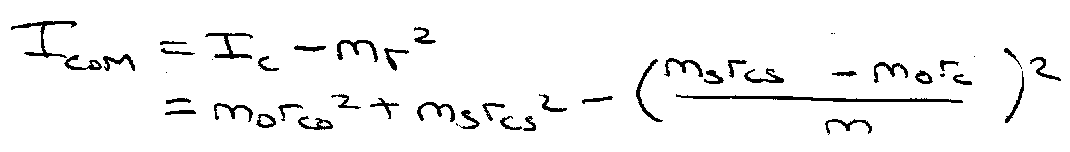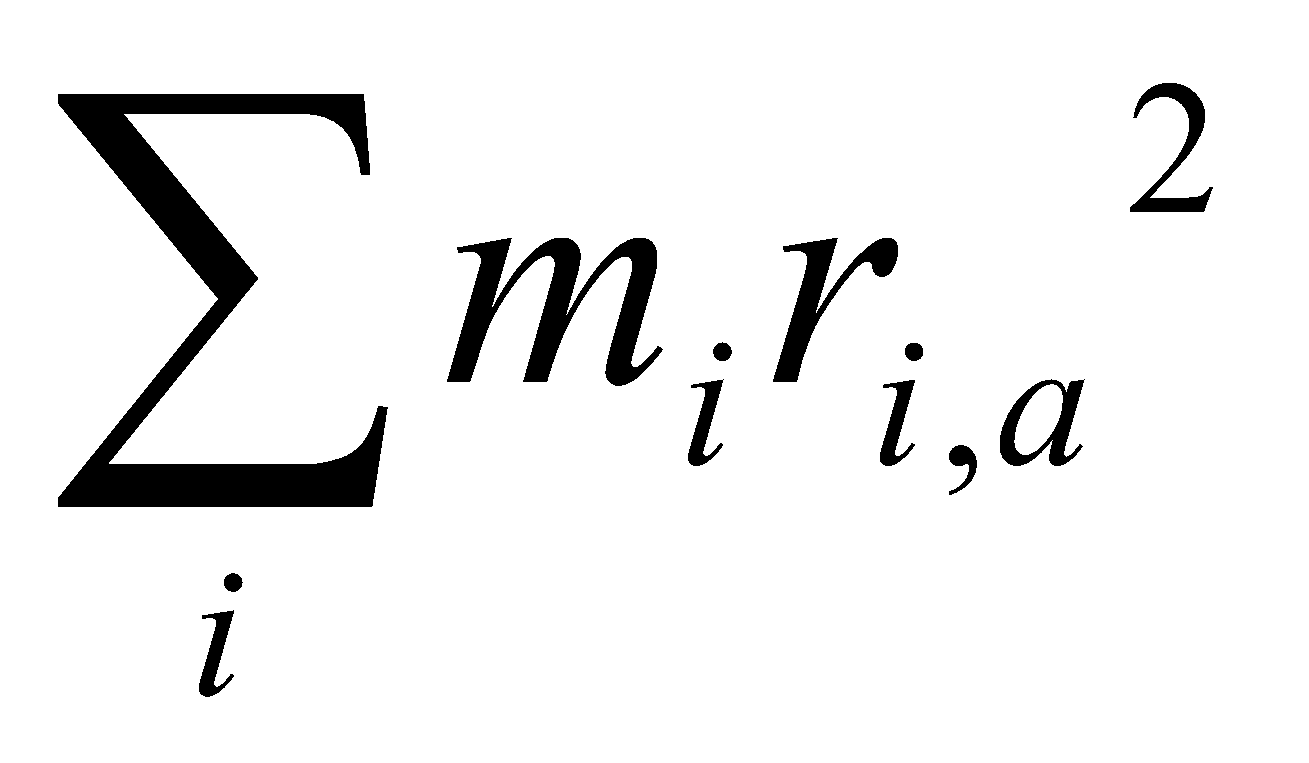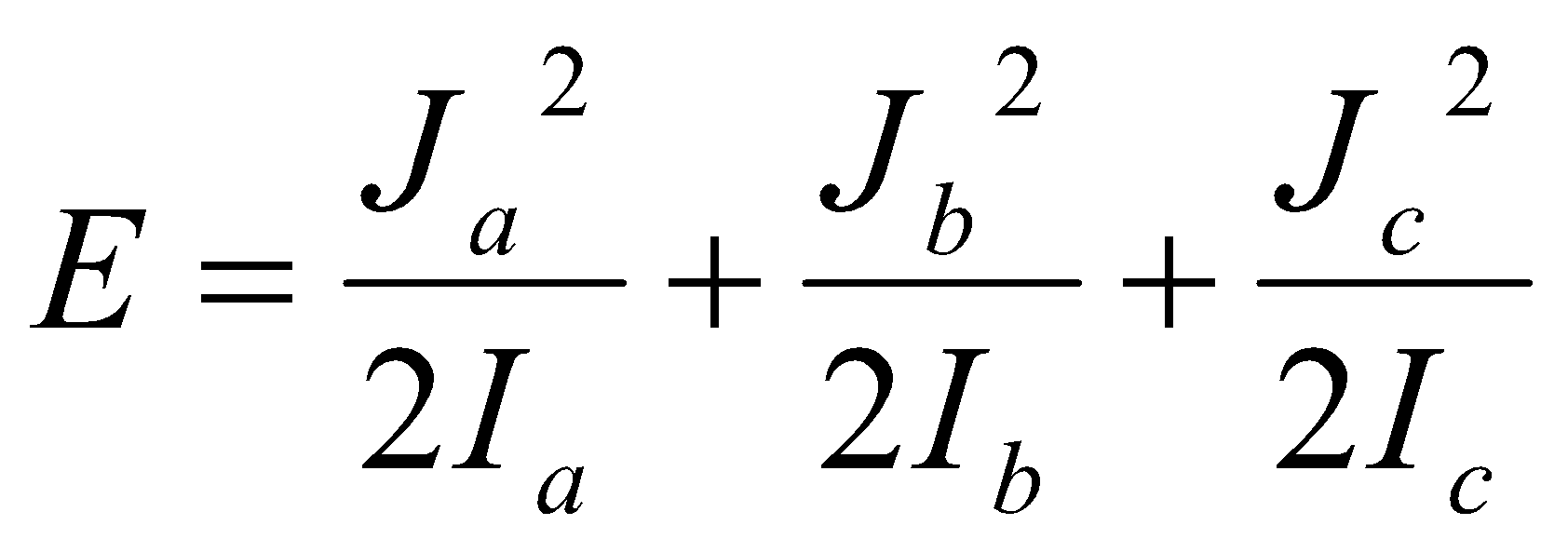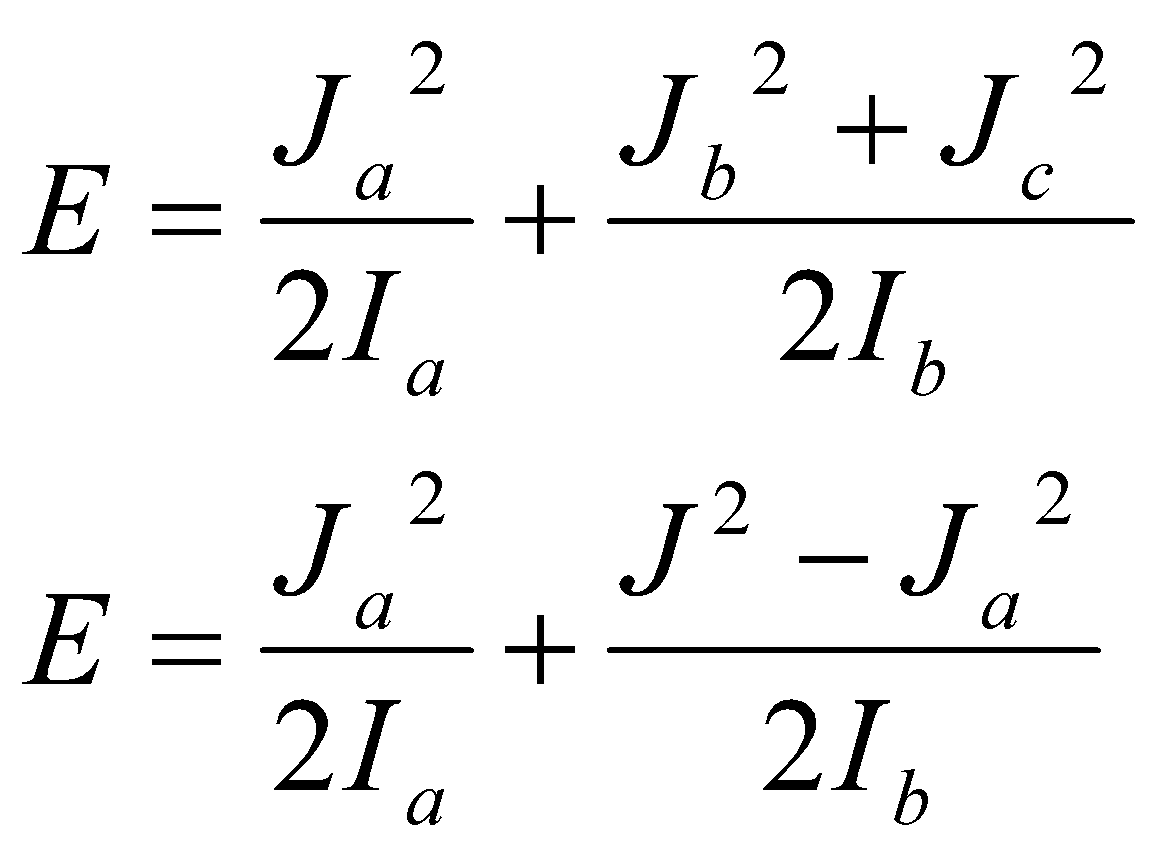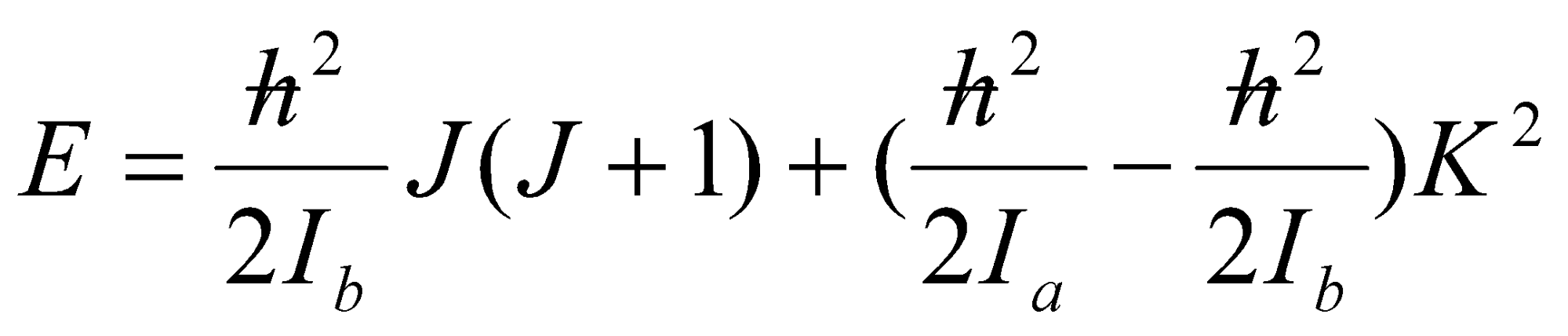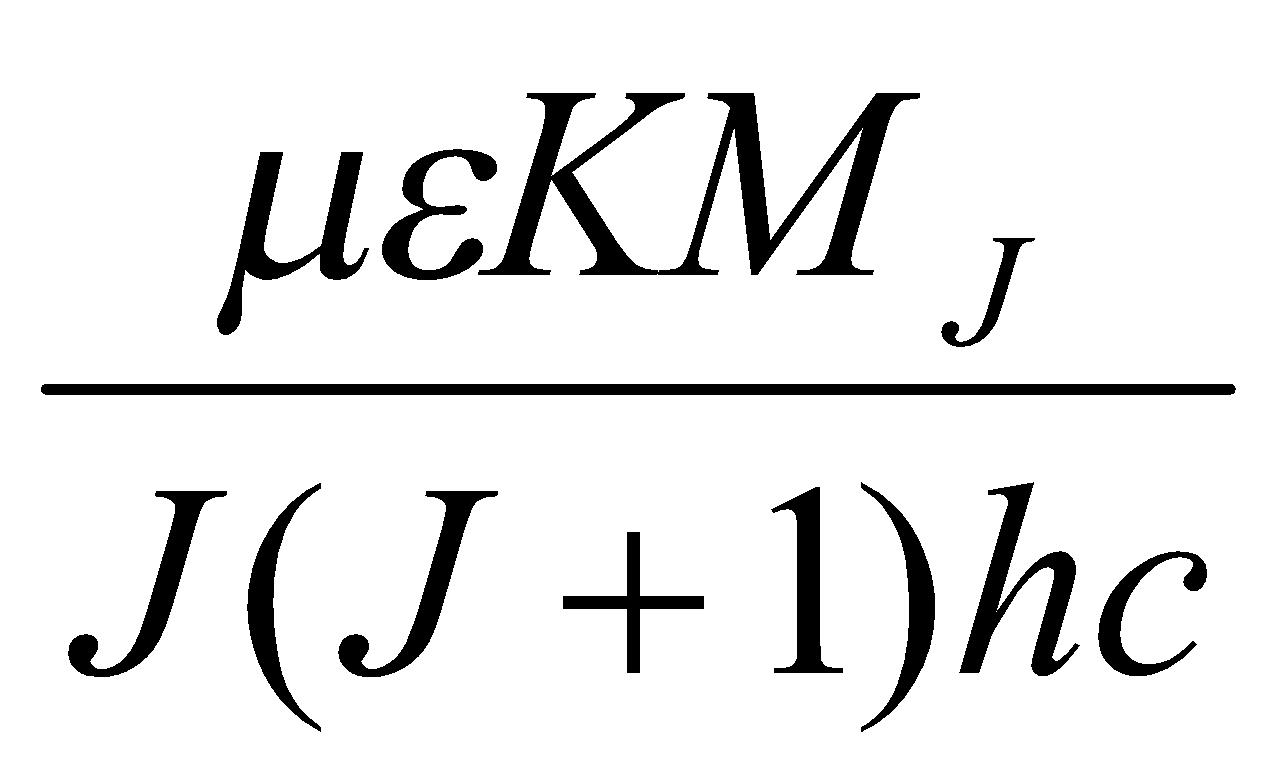Rotational Spectroscopy

SUMMARY:

Linear molecules: E(J) = BJ(J+1) – DJ2(J+1)2

The centrifugal term is needed only for high precision.

Symmetric Tops – E(J,K) = BJ(J+1) + (A-B)K2

K is the angular momentum quantum number for rotation about the symmetry axis.

Molecules include e.g. CH3Cl, benzene.

Selection Rules:

For microwave and far IR spectra:

1. the molecule must have a permanent dipole moment.
2. ΔJ = ±1 (+1 in absorption).

For rotational Raman spectra:

1. the molecule must have anisotropic polarisability (this is all molecules except spherical).
2. ΔJ = ±2 (ΔJ = 0 is the Rayleigh line).

But in Raman spectra of symmetric tops when ΔK ≠ 0, ΔJ = ±1, ±2, ΔK = 0.

Line positions in microwave and far IR –

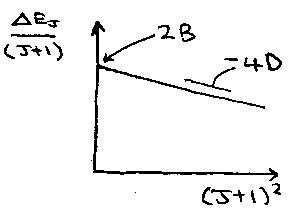
Combining the energy levels and IR or microwave selection rule for linear molecules in the line position v is: v (same units as B and D) = 2B(J+1) – 4D(J+1)3

This comes from: vJ = F(J+1) – F(J) = B0[(J+1)(J+2) – J(J+1)] – D0[(J+1)2(J+2)2-J2(J+1)2]

Adjacent lines are separated by approximately 2B.

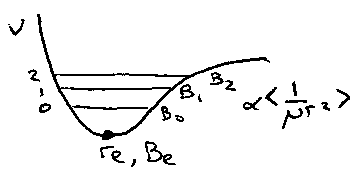
D represents the centrifugal distortion, as bond length increases as rotational energy increases. Thus, the effective value of B decreases with J (proportional to 1/<r2>).

To analyse a microwave or far IR rotation spectrum, use the line spacing to get a rough value of B. Then use B to find the J values for each line. Finally use the full formula for line positions to get precise B and D values by plotting a graph of v/(J+1) against (J+1)2, where intercept = 2B, slope = -4D.

Note though that for the equilibrium bond length to be calculated, extrapolation is required (i.e. Be does not equal B0, B1, etc). The more data that can be obtained, the more accurate the extrapolation will be.

Line positions in Rotational Raman Spectra –

Displacement from the Rayleigh line Δv is 2B(2J+3). Line spacing is 4B. The line positions are never so precise as to need a centrifugal term.

Level populations and line intensities –

The number of molecules in energy level Ej is:

Nj = N0 gj exp (-Ej/kBT), where gj is the degeneracy.

Line intensities are proportional to Nj. In the simplest case (unsymmetrical diatomic or linear molecule), the degeneracy is (2J+1). By differentiating you can show that in this case maximum population is at Jmax given by:

Jmax = (kBT/2B)1/2 – ½

This comes from differentiating NJ by J. (kBT and B must be in the same units! - cm-1 or Joules)

In spectra of symmetrical linear molecules nuclear spin must be included in the degeneracy – there is alternation of intensity if the nuclear spin of equivalent nuclei is non-zero (H2, N2, F2 etc). If the nuclear spin is zero, half the lines are missing and the line spacing is 4 or 8B (e.g. O2, CO2). For nuclear spin I, intensity ratio approaches (I+1)/I at high J.

Energy Levels

EJ = BJ(J+1)

Considering centrifugal distortion (bond stretches) –

EJ = BJ(J+1) – DJ2(J+1)2

Diatomic –

m1 and m2 point masses.

Rigid rotor length r.

Erot = ½ Iω2

I = m1(z1-z)2 + m2(z2-z)2, i.e.

I = μr2

Erot = ½ (p2/I), p = Iω 

Hence,

Hrot =

Find eigenfunctions and values.

→ J2 ψJM = J(J+1)ψJM

Therefore,

Erot =, J = 0,1,2…

Implies:

B = h2/2I, rotational constant (Joules).

B = h2/2hI (Hz)

B = h2/2hcI (cm-1)

ψJM – spherical harmonics. Rotational coordinates θ, φ. Quantum numbers J and M → Jzψ = MJψ, MJ = -J …+J

Note that E = BJ(J+1) implies independent of MJ (in the absence of external electric / magnetic fields).

Each rotational level J is (2J+1) fold degenerate.

Note also parity labels on J:

J odd → negative

J even → positive

Selection Rules –

ΔJ = 0, ±1

ΔΛ = 0

parity +↔-

ΔJ = +1 most relevant to closed shell diatomic, as 1Σ+ is a given (parity).

Allowed transitions for E = BJ(J+1) are thus:

hv = B [J(J+1)(J+2) – J(J+1)] = 2B(J+1)

Spectrum consists of equally spaced lines starting as v = 2B/h and separated by 2B/h.

Rotational transitions occur from microwave up to far-infrared.

Populations:

(N’’ – N’) = N’’(1- e-hv/kT)

hv << kT (for rotational region), therefore population of upper M state involved in the transition is not negligible compared with lower. Absorption intensity is a measure of population difference.

Expand,

(N’’-N’) = N’’(1-1+hv/kT - …)                -        linear with v.

N’’ = No e-BJ(J+1)/kT                                in terms of J = 0 level.

Centrifugal Distortion

Not exactly 2B/h spacing, but get slightly closer as increase J.

This is because bond is not infinitely stiff. Faster rotation → masses move apart, I increase and B decreases. Use Hooke’s Law, F = -k(r-re) = -μrω2

Stretching bond contributes to rotational energy as Kinetic and Potential. Summing these for total centrifugal contribution:

Hence,

Erot = BJ(J+1) – DJ2(J+1)2, where D =

Hence, a J+1 ← J transition has frequency v = 2B(J+1) – 4D(J+1)3

v/(J+1) = 2B – 4D(J+1)2 

– plot v/(J+1) against (J+1)2 gives intercept 2B and slope -4D.

Determining Bond Lengths –

Can relate B to I and so obtain r.

Note though that there is a weak vibrational dependence as:

Bv = Be - αe (v+½) + …

where αe is a vibrational coefficient (harmonic and anharmonic contributions).

Bv gets slightly smaller as v increases.

Be μ-1

αe μ-3/2

Simplest way is to measure Bo and Do for diatomic in its zero point level. Bo gives ro, and ro is averaged over the v = 0 wavefunction.

More accurate – measure several vibrational levels and extrapolate back to Be (equilibrium rotational constant), which gives re.

Stark Effect –

The effect of an external electric field on the spectrum.

Wstark = - μ.E        [ negative as energy lowest when dipole and E-field parallel ]

Difference to electric dipole transition is that apply a static, time-independent field.

When field is large, there is extensive mixing and J-values cannot be assigned.

J and parity no longer good quantum numbers.

M remains good. E-field causes the molecule to rotate “cock-eyed” about the field direction rather than having rotational angular momentum vector point in a fixed direction.

There are 1st order and 2nd order Stark effects. 1st order is very rare – requires vibration/electronic degeneracy in rotational energy levels. One diatomic example is NO (2Π electronic ground state).

2nd order → closed-shell electronic and rotational level has only (2J+1) degeneracy.

Summary:

F(J) = EJ/hc = BJ(J+1) – DJ2(J+1)2, J = 0,1,2…

B – rotational constant = h/8π2Ic                        (cm-1)

I – moment of inertia = μR2                                 (kg m2)

R – internuclear distance                                 (m)

μ - reduced mass                                         (kg)

D – centrifugal distortion constant = 4B3c2/v2         (cm-1)

v – vibrational frequency = (1/2π)(k/μ)1/2                 (Hz)

Degeneracy 2J+1

NJ = No(2J+1) exp (-BhcJ(J+1)/kT)

(NJ = number in level J)

Maximum population: dNJ/dJ = 0 → Jmax = (kT/2hcB)1/2 – ½

Isotope Effects in Linear Polyatomics –

Spectra for polyatomics same form as diatomics.

B depends on more than one bond length.

I = for a linear polyatomic.

ri – distance to centre of mass.

Parallel Axis Theorem:

Determine rco, rcs by isotopic substitution.

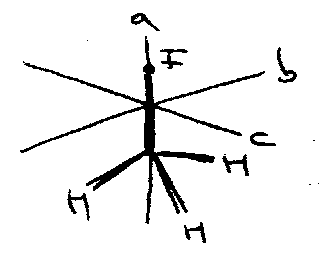
Polyatomic Non-Linear Molecules –

Define axes through Centre of Mass, such that one axis has largest possible I and one perpendicular has the smallest.

CH3I:

e.g. Ia =

c axis has largest I, while a axis has smallest.

Spherical Top –

e.g. SF6.

Ia = Ib = ic, E = J2/2I.

Quantum: <J2> = J(J+1)h2

E = hcBJ(J+1)

(B = h/8π2Ic)

Symmetric Top –

Any molecule with at least one n-fold axis of rotation.

e.g. NH3, benzene (n ≥ 3).

PROLATE:         Ib = Ic > Ia (CH3F)

OBLATE:        Ic > Ia = Ib (benzene)

Prolate,

Ja is component of angular momentum along the molecule-fixed a axis.

By analogy,

<Ja> = Kh.

K is a projection quantum number along a axis. K = 0, ±1, … ±J.

→

F(J,K) = BJ(J+1) + (A-B)K2                [ A > B ]

Oblate, same but:

F(J,K) = BJ(J+1) + (C-B)K2                [ C < B ]

If K = J – rotational motion is primarily about the top axis.

Selection Rules:

ΔJ = ±1, ΔK = 0 (dipole unchanged through rotation about symmetry axis).

F(J+1, K) – F(J,K) = v = 2B(J+1)

Taking into account centrifugal distortion,

F(J,K) = BJ(J+1) + (A-B)K2 – DJJ2(J+1)2 – DJKJ(J+1)K2 – DKK4

V = 2B(J+1) – 4DJ(J+1)3 – 2DJK(J+1)K2

Stark Effect – lifts M degeneracy –

MJ space-fixed projection quantum number.

F(J,K,MJ) = BJ(J+1) + (A-B)K2 +

Asymmetric Tops –

Ia ≠ Ib ≠ Ic.