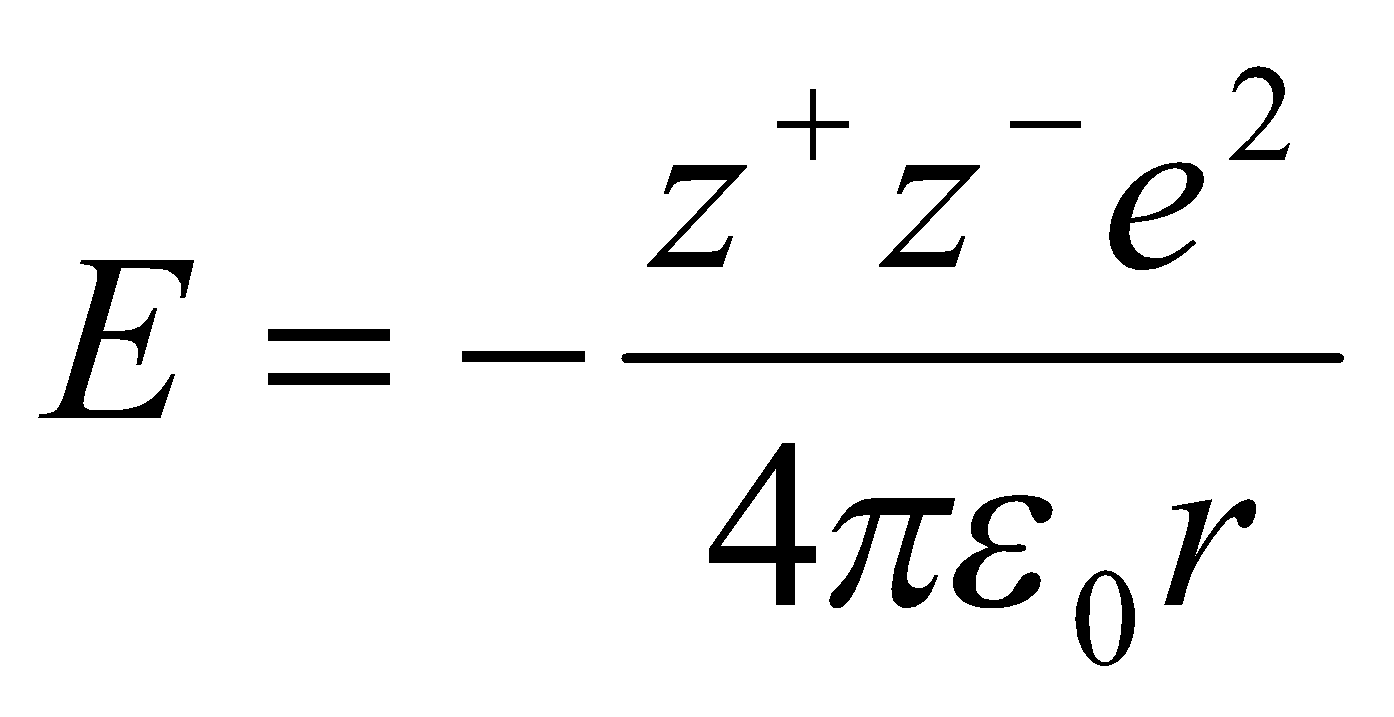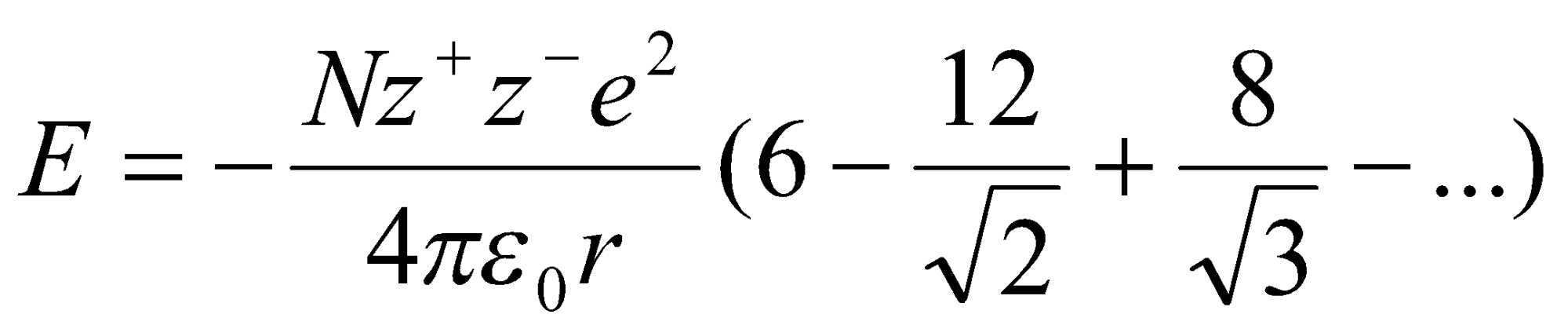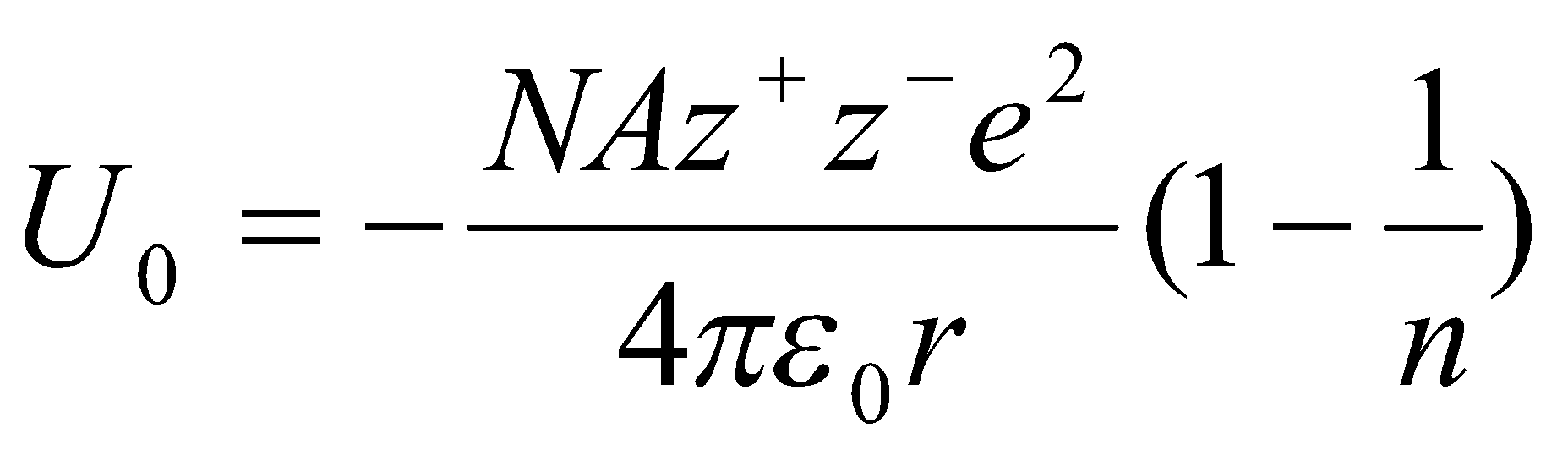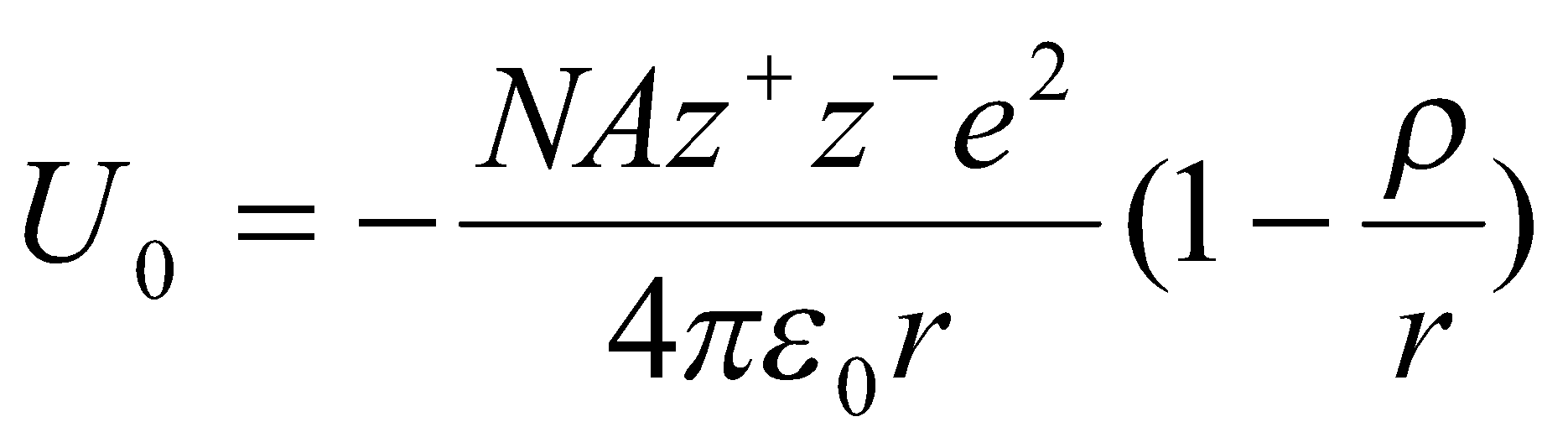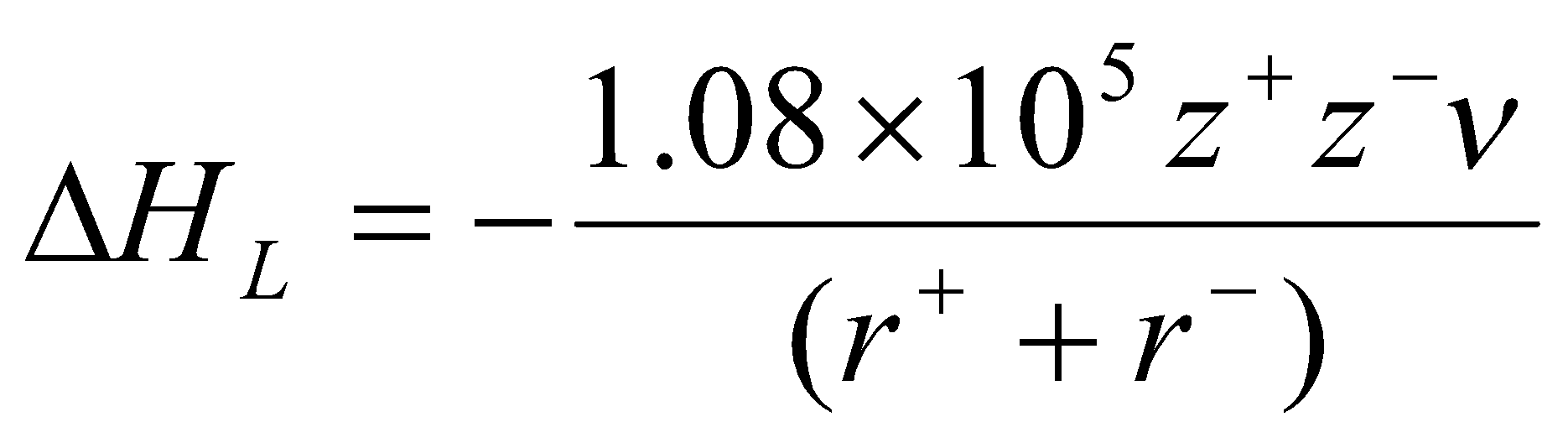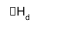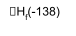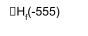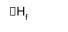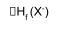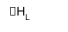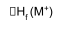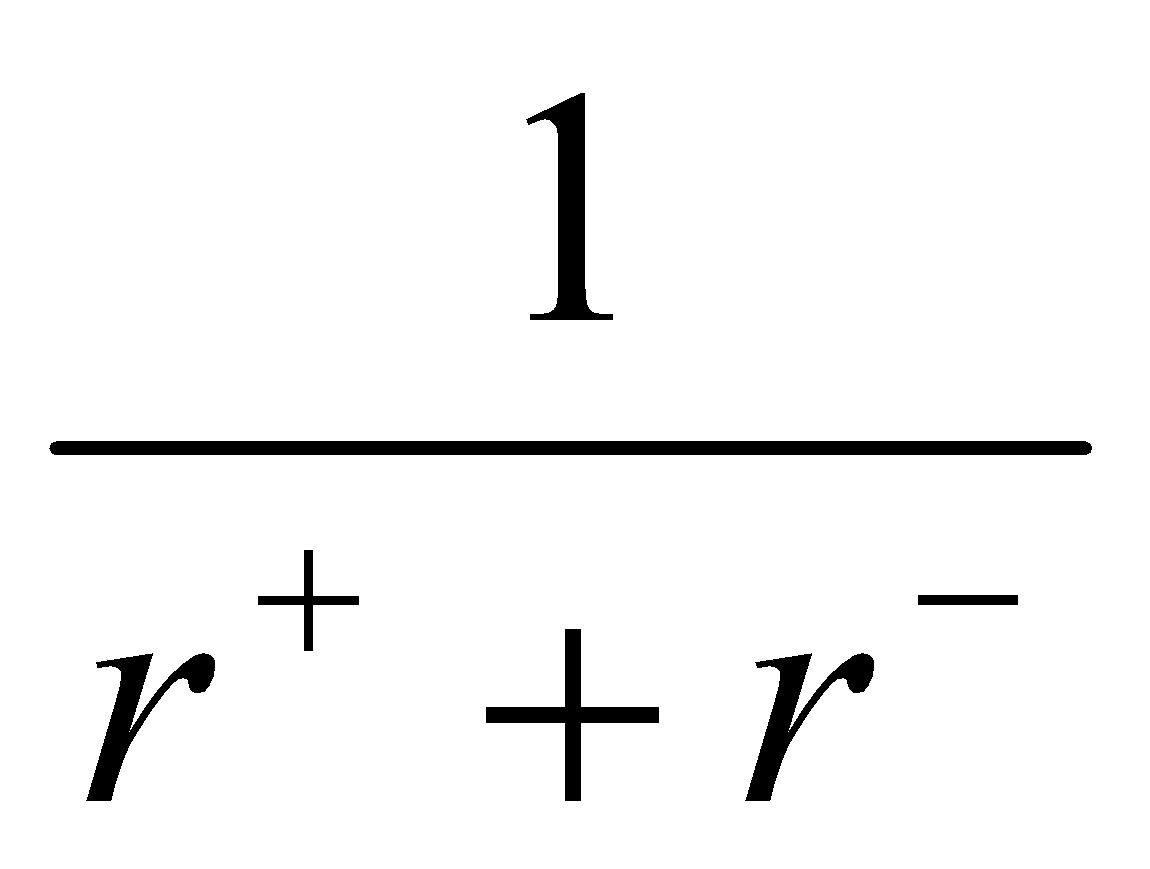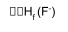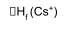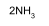Pre-Transition Metal Notes

The Ionic Model

Groups 1 & 2, plus the Lanthanides (f-contraction → little covalency). Provides simple equations for calculation of interaction energies between ions (ΔHL) and dipolar molecules (e.g. ΔHhyd).

Evidence for the existence of ions:

Electrical conductivity when molten or dissolved in polar solvents.

Electronic Spectra (charge transfer) – similarity between spectra of gas phase/solutions and solid compounds.

Magnetic – unpaired electrons. Similarity between gas/solid again.

Electron-density measurements – x-ray diffraction data along the internuclear axis.

Lattice Enthalpy

ΔHL of a compound MX is  the enthalpy change when:

MX(s) → M+(g) + X-(g)

Can be found by using Born-Haber Cycles (Enthalpy is a state function).

For NaCl:                                                        ΔHo / kJ mol-1

(2)        NaCl(s)        →        Na(s) + ½ Cl2 (g)                411

(3)        Na(s)                →        Na(g)                                107

(4)        Na(g)                →        Na+(g) + e-(g)                        502

(5)        ½ Cl2(g)        →        Cl(g)                                122

(6)        Cl(g) + e-        →        Cl-(g)                                -368

Summing all the reactions above, we have:

NaCl(s)                →        Na+(g) + Cl-(g)                        774 (ΔHLo)

Notes:

• the reverse of equation (2) is the definition of the standard enthalpy of formation of solid NaCl.
• Equations (3) and (4) together define the standard enthalpy of formation of Na+(g).
• Equations (5) and (6) together define the standard enthalpy of formation of Cl-(g). Notice that the enthalpy change (5) is half the bond enthalpy of the chlorine molecule.

Thus,

ΔHL [NaCl(s)] = ΔHf [Na+(g)] + ΔHf [Cl-(g)] - ΔHf [NaCl(s)]

ΔHf [NaCl(s)] = ΔHf [Na+(g)] + ΔHf [Cl-(g)] - ΔHL [NaCl(s)]

Electrostatic Interactions –

It is known that:

        (Coulomb)

So for NaCl, each Na has 6 Cl ions as nearest neighbours distance r away, then 12 Na ions as next nearest neighbours distance r2 away, and so on.

Summing the attractive and repulsive terms, the total electrostatic interaction can thus be expressed as:

The series in brackets converges to a constant, the Madelung Constant, A. It is entirely geometric in origin.

When considering the short-range repulsive interactions, it can also be suggested that E = B/rn, where B is a constant and n is the Born-Exponent.

Then by differentiation we obtain the Born-Lande Equation for the total Energy:

Similarly, if E = ae-r / p for short range repulsive interaction instead, then we get the Born-Mayer Equation for lattice energy:

These equations imply that ionic attractions are a long range force (1/r), compared to covalent (nearest neighbour) and van der Waals (1/r6).

They depend only on the radius of the ions, which implies that same radius = same behaviour. Properties independent of nature of ions.

The degree of packing in the structures depends on the Madelung Constant (not Radius/Ratio Rules! - unreliable).

The Kapustinskii Equation

Ratio of Madelung Constant to total number of ions per formula unit (ν) for a series of compounds are very similar. Thus, the variation of A/νr between structures is very small.

The following approximations are made:

1. replace A with 0.87ν.
2. internuclear distance taken as sum of ionic radii.
3. Value of n=9 for NaCl can be taken as average for all structures.

This gives:

 where r is in pm, and H in kJ mol-1.

Needs only ionic radii. Accurate to within 10% of experimental values.

Estimating Ionic Radii –

Lande:

Suggested that in LiI, with a small cation and a large anion, the large I- are in contact and hence from the unit cell parameter an ionic radius of I- can be derived. By examining other metal halides a table of ionic radii could be drawn up.

Pauling:

Theoretical basis: in many-electron atoms and ions, screening and penetration effects result in the electrons experiencing an effective nuclear charge, Zeff = Z - σ, where σ is the screen constant calculated using Slater’s Rules. Pauling therefore propose that:

Rionic = Cn/Zeff = Cn/(Z-σ), where Cn is a constant depending on the principal quantum number n. For isoelectronic ions such as Na+/F-, K+/Cl-, Mg2+/O2-, the Cn values for the pairs should be the same. Thus,

r(Na+)/r(F-) = [ Z(F-) - σ ] / [ Z(Na+) - σ ].

Knowing r(Na+) + r(F-) from crystallographic data, the ionic radii can be calculated.

Shannon and Prewitt:

Compiled unit cell data for more than 1000 compounds and evaluated a set of self-consistent ionic radii which can best reproduce the experimentally observed internuclear distances. They based their data set on r(O2-) = 140pm and r(F-) = 133pm. The values they obtained were in good agreement with those from other methods. The Shannon-Prewitt ionic radii are the most commonly used data set.

Thermochemical Radii:

Ionic radii for complex ions such as NO3, CO32-, SO42-, NH4+. Use a Born-Haber cycle to calculate the lattice enthalpy, then the Kapustinskii equation to calculate (ra++rb-), knowing ra+ one can calculate rb-.

Trends in Ionic Radii

1. For isoelectronic pairs, the cation is smaller than the anion.
2. Across a row, radii of isoelectronic cations decrease rapidly, but the change in anionic radii is less pronounced. Electrons added to the same shell (Zeff increases).
3. Down a group the radii increase. Electrons are added to extra shells, and penetration (increase Zeff) not as dominant as increasing n.
4. Ionic radii depend on coordination number. Increase slightly with CN. This is due to increased anion repulsion around the cation.
5. d/f contractions. Thus Group 11 & 12 ions are smaller than Group 1 and 2. 3d/4f orbitals are non-penetrating and so poor shielders, which causes Zeff to rise.

“Diagonal Relationship” – r (Li+) r (Mg2+), and similarly r(Na+) ≈ r(Ca2+). This is due to points 2 and 3, and often leads to similar chemistry (e.g. isostructural compounds).

Covalency

This effect causes lattice enthalpy and solvation energy to increase (not expected from the Ionic Model).

Covalence should be considered for polarisable anions (large, low electronegativity) and polarising cations (Z2/r, i.e. small or highly charged, e.g. Be2+, Zn2+).

Formation of Ionic Compounds by the Alkali and Alkaline Earth Metals

Reaction	Product	Anion	Comments
M + ½ X2 → MX	Halide	X-	Group 1 elements also form polyhalides, e.g. K+[ICl4]-
2M + ½ O2 → M2O	Oxide	O2-	Normal product of combustion in air for Li, Mg, Ca. Suboxides also formed by Rb and Cs, e.g. Rb6O, Rb9O2, Cs11O3. Basic: M2O + H2O → 2MOH.
2M +O2 → M2O2	Peroxide	O22-	Normal product of combustion in air for Na, Ba
M + O2 → MO2	Superoxide	O2-	Normal product of combustion in air for K, Rb, Cs
3M + ½ N2 → M3N	Nitride	N3-	Only formed by Li in Group 1, Mg → Ba (M3N2) in Group 2. Basic: Li3N + H2O → LiOH + NH3.
2M + 2C → M2C2	Carbide	C22-	Readily with Li, Ca, Sr, etc at elevated temperature. Basic: CaC2 + 2H2O → Ca(OH)2 + C2H2.
M + ½ H2 → MH	Hydride	H-	Formed at high temperature (Mg requires high pressure), saline hydrides. Basic: MH + H2O → MOH + H2.
M + H2O → MOH + ½ H2	Hydroxide	OH-	Oxides and hydroxides strong bases. Absorb atmospheric CO2 to give M2CO3 and MHCO3 (Na and K).
M + NH2 → MNH2 + ½ H2	Amide	NH2-	Reaction with gaseous NH3 at high temperature, or the metal with liquid NH3 and a transition metal ion such as Fe3+ as a catalyst.

[ M = 1 mole of a Group 1 metal or ½ mole of a Group 2 metal ].

Solid Compounds of G1 & 2

All form stable binary halides, oxides and hydroxides with the group oxidation state.

+1 state of Group 2 is unstable wrt disproportionation.

Disproportionation

Group 1:

CsF2                               CsF + ½ F2

                                           Cs + F2

ΔHd = +138 – 555 = -417 kJ mol-1

Actually unstable wrt CsF, even though stable wrt elements (see below).

Group 2:

Ca + ½ Cl2 → CaCl.

ΔHf = -93 kJ mol-1, i.e. CaCl is stable wrt the elements.

But, 2CaCl → Ca + CaCl2.

ΔHd = -610 kJ mol-1. Unstable wrt disproportionation. Common in Group 2 for M+.

Stability of compounds with small anions (F-, H-) decrease down the groups, while stability increases for large anions. Exception is Mg.

Stability of halides decreases down the halide group, but the decrease is less severe for large cations.

Only Li of Group 1 forms stable nitride. All Group 2 form nitrides.

Structural Chemistry 

(see Tutorial 1 for more detail)

All hydrides, halides and hydroxides of Group 1 have Rock Salt structure except CsCl, CsBr, CsI. All oxides have anti-fluorite structure except Cs2O. Superoxides (MO2) have pyrite structure.

Group 2 Oxides except BeO have Rock Salt structure. Most of the fluorides are fluorite structures, except BeF2 / BeF4 which are tetrahedral chains, and MgF2 which is rutile. Other halides are difficult to predict and tend to adopt distorted/layered structures due to polarisability. CN > 8 for some Barium compounds.

As cations increase in size, the thermal stability of compounds with large complex ions increases. For example, heating Li in air gives the oxide, Na on the other hand forms peroxide, while the other Group 1 elements for superoxide. Rb and Cs also form a series of sub-oxides with unusual structures based on OM6 octahedra.

Heating the nitrates of Group 1 gives nitrites, except Li which forms the oxide. Stability of carbonates, sulphates, etc. increase down the group.

The ionic model can also predict the course of reactions using lattice enthalpies. For example,

LiI + NaF → LiF + NaI

2NaF + CaCl2 → 2NaCl + CaF2

These occur because the lattice enthalpy of LiF and CaF2 is very high (the latter despite r(Na+) ≈ r(Ca2+)).

But there are notable exceptions, especially those involving complex ion salts:

NaNO3 + KCl → NaCl + KNO3

NaNO3 + LiCl → NaCl + LiNO3

Both reactions found to be thermodynamically favourable even though r(Cl-) < r(NO3-). Here we expect the combination of the smaller Na+ and Cl- to provide the lattice enthalpy driving force for the first reaction, but on these grounds the second reaction should not proceed. Apparently, there is stronger than expected interaction between the small Li+ and the non-spherical nitrate ion.

Also the following reactions:

AgF + KCl → AgCl + KF

HgF2 + 2KCl → HgCl2 + 2KF

In these two reactions, the substantial non-ionic contributions to the lattice enthalpies of AgCl and HgCl2 provide the driving force.

Trends in Stability

M(s)         +         ½ X2(g)    →         MX(g)

       M+        +                 X-

ΔHf = ΔHf(M+) + ΔHf(X-) - ΔHL

For a given anion:

1. ΔHf (M+) decreases down the group. Both ΔHatom & EI decrease.
2. ΔHL so ΔHL decreases down the group.

Thus, have to look at which factors change by the greatest amounts to determine stability.

ΔHL can be controlled. If r- is small, then the proportional decrease in ΔHL is large (by differentiation). If r- is large, the ΔHL decreases slowly.

Nitrides:

For Group 1, only Li is sufficiently small to form Li3N. All other M3N compounds are endothermic. This is because ΔHL is large with the small Li+ ion, whereas Na+ is too large.

For Group 2, z+ = +2, and ν = 5, gives a very large ΔHL. All form M3N2.

Both Group 1 and Group 2 trends can be justified by the Kapustinskii Equation.

Hydrides:

Much less stable than F/O compounds. Not due to polarisability of H- though. The ΔHf of H- is +140 kJ mol-1, compared to -271 kJ mol-1 for F-. H-H bond is very strong, while the F-F is weak (due to lone pair repulsions).

Halides:

For halides in general, the stability increases down the group as it gets easier to form the metal ions due to the valence electron being in a higher energy orbital. This term dominates.

However, with fluorides, the small radii means that the lattice enthalpy term is quite large and is responsive to changes in cation size, and so with increasing cation size, the lattice enthalpy is very small and so they are less favourable down the group.

Oxides:

For group 2 the stability of the oxides decreases as the lattice enthalpy term is getting much smaller.

For group 1, the situation is complex as there are many types of oxides besides O2- that can form, and so the stability isn't simply with respect to the elements. With respect to the elements the stability decreases down the group. It should be noted however, that compounds such as Na2O2 and NaO2 are formed as well as Na2O.

Oxy acid salts:

In general, stability with respect to elements falls down the group, but the stability with respect to the oxide increases. With a large cation, there is very little change in lattice enthalpy on decomposition (i.e. BaCO3→BaO) and so decomposition is not very favourable. But if you have a small cation like Mg, the large change makes the oxy acid salt unstable.

Thermodynamics of Ionic Systems

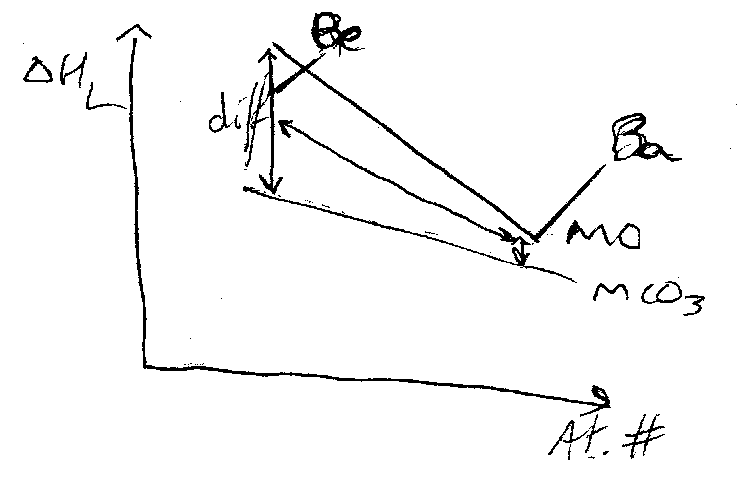
Useful for explaining stability, e.g. CaCO3 decomposes at 900oC, but MgCO3 decomposes at 400oC.

Start by drawing the cycle:

Also, always define the decomposition temperature.

Decomposition occurs when ΔG for the reaction is negative. In this case, the ΔSdecomp term is dominated by the gas produced (CO2) and so is positive and effectively constant.

Note that Tdecomp is proportional to ΔHdecomp, i.e. when ΔH is positive (endothermic), higher temperatures of decomposition are expected.

The thermodynamic driving force is a gain in lattice energy with smaller anion. This implies it is more important for small cations, i.e. smaller M2+ carbonates have lower decomposition temperatures. Hence, large cations stabilise large anions, but this is NOT because of packing.

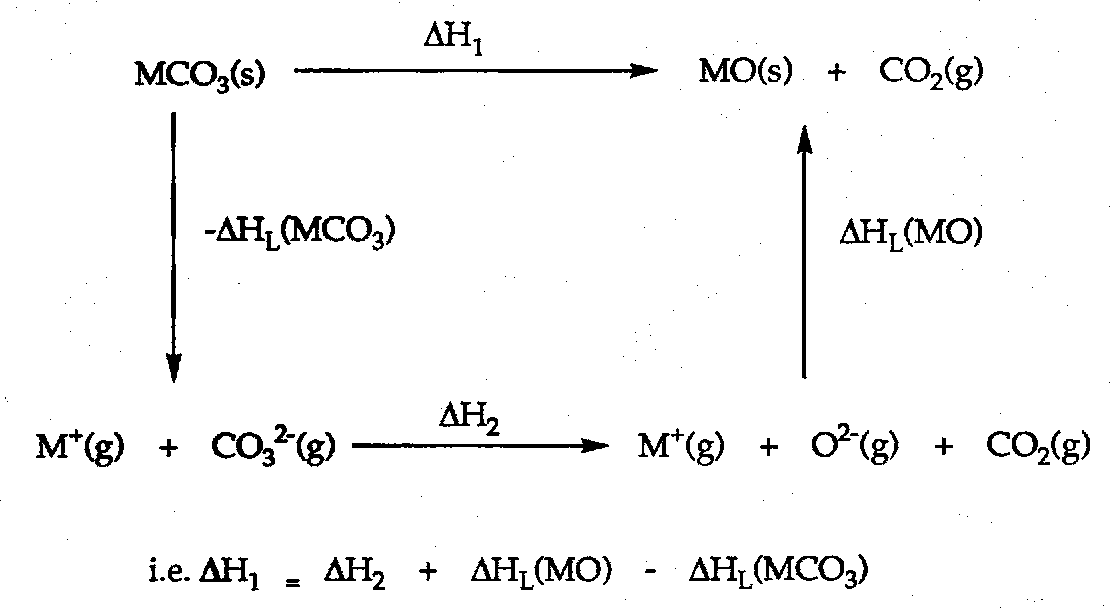
This can be explained by using the cycle above:

MCO3:         ΔHL = (A.2.2.2)/(r2++r(CO32-)).

MO:         ΔHL = (A.2.2.2)/(r2++r(O2-)).

ΔH1 = [ (8A/(r2++r(CO32-)) – (8A/(r2++r(O2-)) ]+ ΔH2

i.e. to stabilise MCO3 want to minimise difference in ΔHL:

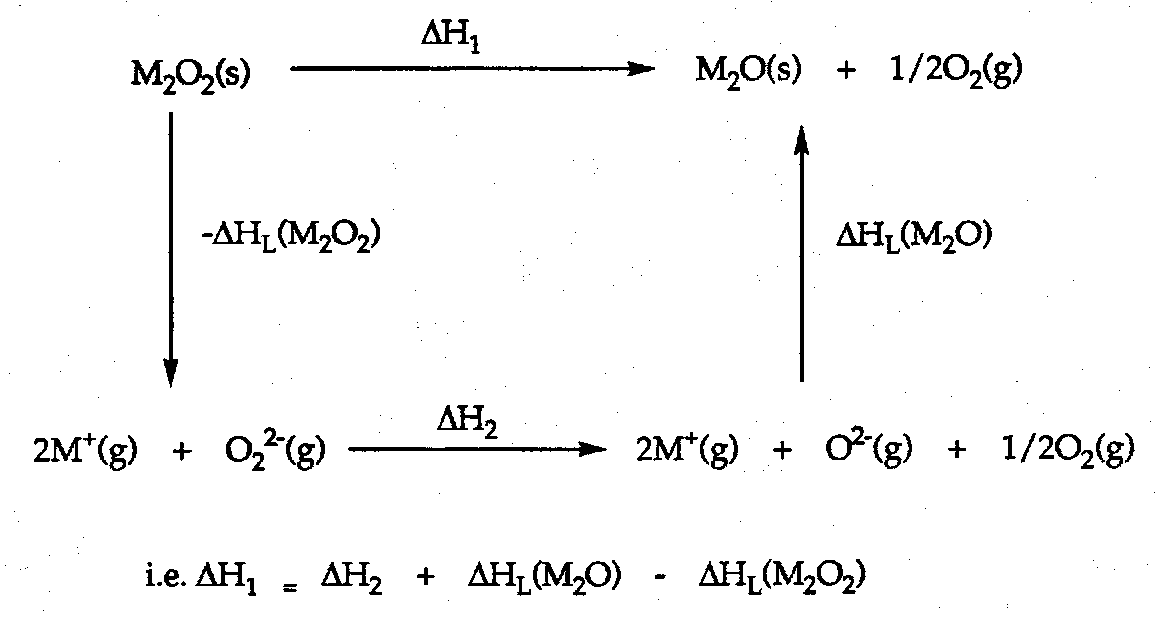
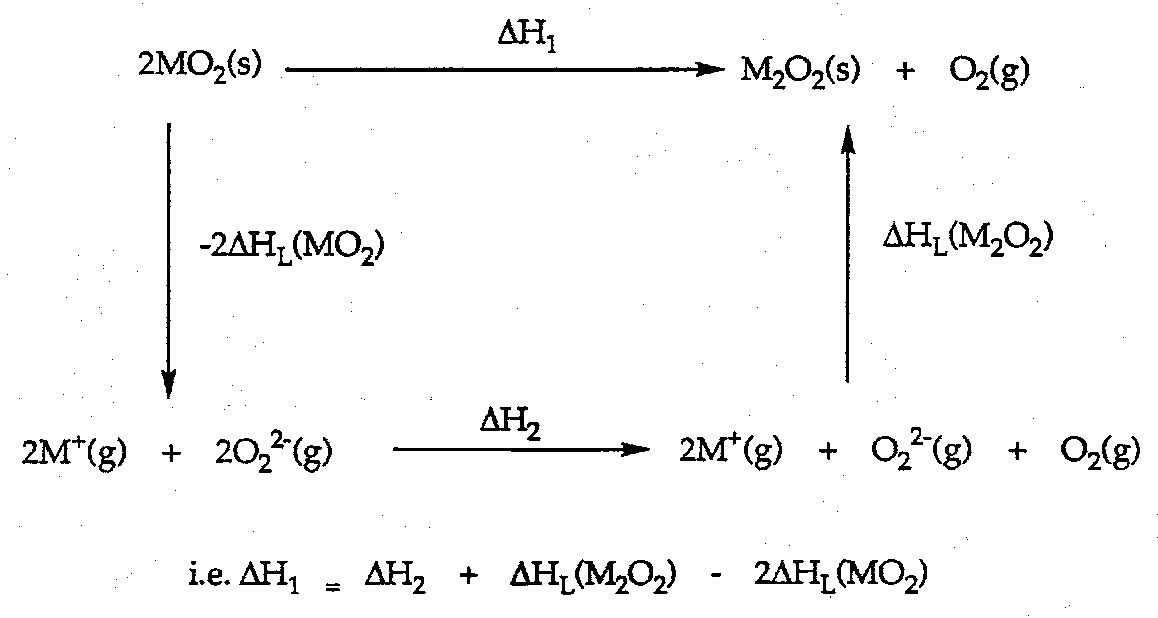
As another example, consider the Group 1 Oxides.

Burning in excess O2 gives:

Li → Li2O

Na → Na2O2

K → KO2

Cs → CsO2

Why? Look at thermodynamic cycles.

e.g. for Rb+O2- superoxide.

UL = 1.08x05x2x1x1 / (166+181) = 622.5 kJ mol-1.

Similarly for Rb+2O22-.

UL = 1825 kJ mol-1.

ΔHdec = 2ΔHL(RbO2) - ΔHL(Rb2O2) + ΔHf(O22-) – 2ΔHf(O2-).

ΔHdec = 2(622.5) – 1825 + 520 – 2(-105) = 150 kJ mol-1.

Assume entropy of any solid is identical and insignificant, compared with entropy of gas.

ΔSdec = So(g) = 205 J K-1 mol-1.

This then allows the decomposition temperature to be calculated.

Comparison of Properties of Group 1 and Group 2

All are soft light metals.

Very reactive. Strong reducing agents.

Group 2 tend to be more stable with respect to elements (e.g. Nitrides). This is due mainly to higher charge, which gives a higher lattice enthalpy:

Comparing Cs and Ca compounds – CsF2 / CaCl both stable wrt elements.

e.g. CsF2(s):

Cs(s)         +         F2(g)           →         CsF2(g)

Cs+         +         2F-

 Negative ΔHL → stable wrt the elements.

Similar calculations show that CaCl is also stable wrt to the elements.

Stability of Oxidation States:

2nd Ionisation Energies vs. Difference in Lattice Enthalpy.

For Cs, difference in ionic radii is small (167 vs. 150pm), whereas much larger difference for Ca (170 vs. 100pm), due to loss of a subshell.

Generalising, Al2+ unstable (→ Al3+). Also, no Tl2+, Pb+, Pb3+, etc.

The change in radii is the key point (from the Kapustinskii Equation).

Similarly, Transition Metals can occupy various oxidation states because the change in radius is small from electrons lost within d-subshell.

Also, for small ions, ΔHL  → ΔHL is large.

Solutions in Liquid Ammonia

Alkali Metals – all look bright blue in liquid ammonia.

High concentrations gives a bronze colour, and the conductivity increases to that of molten metals.

Thus, the metals must give rise to the same species to cause the same colour, and the actual metal does not matter. This occurs because the metal breaks down to M++e-. This electron is then trapped in the linked NH3 molecules (H-bonding as a liquid). The gaps in the NH3 occur as when 2-3 displace, and gives a cavity 300-350pm wide.

This is known from the absorption spectra, which is centred around the infrared region. Thus, it appears blue, irrespective of metal.

The bronze colour appears when the concentration of M+ is so high that this electride (electron coordinated by ammonium ions) associates with the M+ as well.

NB: these solutions require anhydrous conditions and minimal impurities to be stable, otherwise amide formation results.

Also of note, the electride is understandably a powerful reducing agent:

RCH=CH2 + 2eam → RCH-CH22- → RCH2CH3 + 2NH2-

Stability of Complexes

Neutral ligands:

Few stable. Dependent on desolvation of the ions and also metal-ligand attraction. It is the latter which is a problem, since a charged ligand is held more tightly. As it is, the M-L depends on polarity, and water is extremely polar, as shown:

                H                                R

M+        O                        M+        N        R

                H                                R

Charged ligands:

M+ + L- → ML + nH2O

This is now favourable, since the attraction of M+ + L- is much greater than a dipole attraction.

Considering whether enthalpy or entropy drives this reaction, we note that M++X- is good from an enthalpy point of view, but also the loss of ΔHsolv is bad. Thus, ΔHcomplexation ≈ 0. However, ΔS >> 0 due to release of H2O from M+ and X-, so entropy is the driving force for these reactions. This is especially shown by polydentate ligands, where it is possible to free 6 water molecules for one ligand.

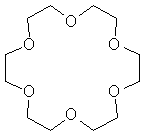
An extreme example of this is with crown ethers. These are in fact uncharged, but the entropy gain is so high that it is possible. A Crown Ether such as 18-crown-6 looks like the diagram on the right.

Unlike the amine ligand above, which can rotate and invert, this crown ether has few degrees of freedom – it is preorganised. Thus, ΔS is much more positive.

Also worth noting is the specificity of these ligands. For example, the 2.2.1 cryptand binds to Na+, while the 2.2.2 cryptand prefers K+. This is useful for isolation purposes. Another isolation effect is:

2Na → Na+ + Na- → [ Na+(crypt) Na- ].

The product is a solid containing an Na- anion.

See Coordination Chemistry Notes for more info on the Chelate and Macrocyclic Effects.

Organometallics

Most heavy metals form very reactive ionic compounds with alkyls, and so don’t last very long. However, the strong polarising nature of Li, Be and Mg mean that covalently bonded structures are possible.

Synthesis:

2 Li + RX → LiR + LiX

This is carried out in ether, and is otherwise in inert conditions. The yield is often poor due to a reaction between LiX and LiR again. Careful choice of RX is required. HgR2 works well.

LiBu + PhI → PhLi + BuI

Also, Grignard Reagents can be formed:

Mg + RX → RMgX

Structures:

Most lithium alkyls exist as hexameric structures, and have similar properties to most covalent structures. The extended structures means they are usually soluble in organic solvents.

 

Solution Equilibria:

From the point of view of Grignard Reagents, a series of equilibrium structures are possible. The following diagram shows this:

Reactions:

Reactions are those expected of carbanions, such as:

Li + HC≡CH → LiC≡CH2

LiR + H+ → Li+ + RH

LiR + R’I → LiI + RR’

LiR + X2 → LiX + RX

LiR + ether yields alkenes and LiOR.

In water, LiPh + CO2 → PhCO2Li → PhCOOH + LiOH

Grignard Reagents are very useful in Organic Synthesis. These usually involve the formation of an unstable product, which then decomposes with acid to the desired product. The G Reagents form RH as they are hydrolysed by water.

Examples:

2RMgX + O2                 →         2ROMgX         →         2ROH

RMgX + R’CN         →         RR’C=NMgX         →         RR’C=O

Biological Roles of Pre-Transition Metals

No redox chemistry, which would be problematic in biological systems. This is because there is no variable oxidation state. For example, the presence of Cu+ could cause O2 to form OH radicals, which then damage DNA.

Other advantages are that they are often not strong Lewis Acids (preventing Acid catalysis, or harmful pH conditions). This usually means they are poor catalysts. Also, since they are highly soluble, they can behave as electrolytes, and aid charge balance (particularly Na and K).

Na+

Important in nerve function in animals. Sodium channels carry an impulse along a nerve fibre, due to solubility and charge balance. Also used to balance concentration gradients in extracellular fluid.

K+

Similar to Na. Intracellular fluid concentration maintenance. Essential for nerve impulse transmission and cardiac function.

Mg2+

Essential for chlorophyll function, so all green plants depend on it. Also has enzyme activating properties in all animals.

Ca2+

Structural component – shells, bones, cell walls. Involved in blood clotting – enzyme activator. Also essential in muscles and nerve synapses.

Similarities between Groups – Li and Be

These elements have properties which often don’t fit well with the others in their groups, because of their small size.

For example, LiF is very insoluble compared with other alkali metal fluorides. This is due to very high lattice enthalpy. As noted earlier, Li is the only G1 element capable of forming a solid with N3-, again because of its tendency to form structures with high lattice enthalpies.

Be is even more unlike its relatives. In fact, as is true with many periodic arrangements, the properties of Li are related to Mg (diagonally down to the right). Be is similar to Al in that respect, and this is true when noting that Be forms mainly covalent structures. A good example is [Be4O(acetate)6], a large covalent complex structure which solvates in organic solvents. The Be4O is tetrahedrally arranged, with Be continuing its extended covalent bonding around a central O atom.