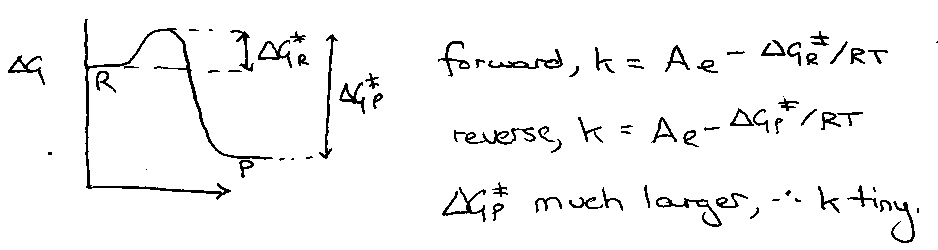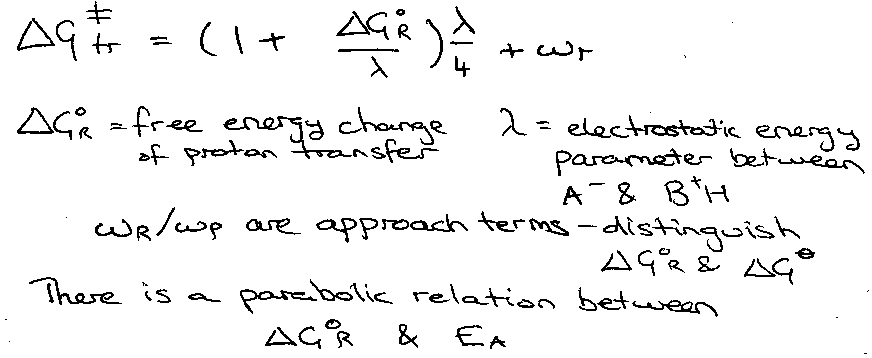Physical Organic Notes

Kinetic Isotope Effect

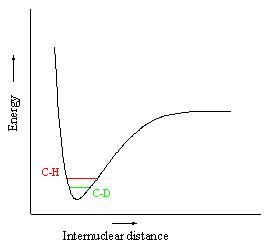
The Kinetic Isotope Effect (KIE) is a useful tool for establishing mechanistic pathways. It comes about by considering the isotopic substitution of D for H in a C-H bond. This causes a change in reaction rate which indicates the involvement of the C-H bond in the mechanism’s rate determining step (terminal KIE).

The effect is brought about by the different vibrational frequencies of C-H vs. C-D (lower frequency due to increased reduced mass). Frequency is linked to energy by E= ½ hv, and hence is linked to rate. Thus when a C-H bond breakage is involved in the rate determining step (RDS), we see a change in Activation Energy due to the KIE. Potential Energy is not dependent on KIE.

Considering Primary Kinetic Isotope Effect (PKIE) – when the C-H bond is key to the rate determining step. This gives a value of kH/kD of up to approx 7. The maximum possible value is 8.8 at 298K, which is brought about by complete vibrational loss of a stretch + 2 bending frequencies. The value does vary with temperature, such that as T decreases, we would expect the ratio to increase in value.

Some examples of where PKIE would be noticeable are any mechanisms where C-H bond dissociation is of prime importance. For example, in the oxidation of secondary alcohols (e.g. by CrO3), the kH/kD = 7.0, indicating that C-H bond cleavage is the RDS. Conversely, in aromatic nitration, the value drops to 1.0, implying that the RDS is addition of NO2+, not loosing H. kh/kD > 2 usually indicates the breaking of C-H in the rate determining step.

The magnitude of the value can indicate either reactant-like or product-like Transition States (see Hammond Postulate below). A low pKIE implies that the C-H bond is either nearly completely broken (close to product), or only slightly broken (close to reactant).

There are also secondary KIE’s possible. In this case the C-H bond is either α or β to the reaction centre. The value of these is usually between 0.7 and 1.5. A value below 1 indicates an inverse KIE, i.e. the rate for C-D is faster than C-H.

The secondary KIE involves tightening or loosening of the C-H bond in the Transition State, but not breaking. It is then labelled as either α or β depending on which carbon the bond is formed with (α being the reaction centre).

α-SKIE results from a change in stretching frequency due to loss of CH to dominate all other terms. The change in rate ratio is usually between 1.15 and 1.2, showing the loss of magnitude compared to the primary KIE. An example of this effect would be something like:

This is typically seen for sp3→sp2 rehybridisation (e.g. in SN1 reactions) and the factors affecting C+ stability are usually apparent. The KIE comes about because of the decreased resistance to bending experienced on the drop to sp2 hybridisation. This has more effect on the freedom of the C-H bond vibration than C-D (since it is longer – see above) so the effect is usually normal (i.e. > 1).

It is possible for inverse KIEs to occur here, e.g. the attack on a carbonyl. This is because in the Transition State the coordination around Cα has increased, which restricts bending. Again this affects C-H more than C-D, but this time in a negative way, so the rate for C-D is greater because it is less destabilised.

β-SKIE is an even more remote effect. It is usually apparent due to conjugated system, where electrons are transferred away from the C-H bond, which weakens it (hyperconjugation):

This is thus a normal KIE. An important point in this case is the conformational dependence which can be useful, e.g. antiperiplanar alignment shows a greater effect than SPP as the orbitals line up appropriately for a greater overlap (and hence more hyperconjugation in effect).

Solvent KIEs are also useful. This would be for example, using D2O instead of H2O. This is often used to determine whether the solvent is in fact a reagent, since this would give a large PKIE. It may also have secondary effects, e.g. in exchange with acidic centres or solvent-solute interactions (affects the energy of the Transition State).

A typical example is where protonation is involved in catalysing a reaction. D3O+ is less stable relative to D2O (due to higher viscosity, and loss of H-bonding) when compared to H3O+ vs. H2O (i.e. the D3O+ is a stronger acid). This means the rate is increased for D relative to H. This leads to an inverse effect. However, H+ transfer in the rate determining step is a primary KIE and so is favoured by H over D (a normal KIE).

Solvent KIEs can be useful for spotting General and Specific Acid Catalysis, by using the normal vs. inverse results:

Isotope Labelling Experiments may also be used to elucidate mechanism. This usually involves ascertaining the location of a given atom in a reaction by substituting it for a detectable element with the same properties. This is typically D or T for H, and 13C or 14C for C. The product or trapped reagents can then be analysed using usually NMR, but also IR/UV spectroscopy, and in the case of 14C, radioactivity measurements.

Linear Free Energy Relationships

Quantitative way of relating structure and reactivity. First showed by observing that the rates of reaction of a series of methyl esters with NMe3 were directly related to the ionisation constants in water of the corresponding carboxylic acids. Thus, a plot of log k for reaction of esters against log K for ionisation of the acids gives a straight line.

Equilibrium constants and rate constants are each related to free energy changes, which implies that there is a linear relationship between the free energy of activation for the ester reaction and the free energy change for ionisation of the acids. This is a linear free energy relationship (LFER).

It was also found when considering this for different isomers, that o-substituted reactants and aliphatic compounds did not obey the linear relationship at all well, but only m and p-substituted ones did very well. This can be explained as the m and p substituents are far from the reaction centre and exert no steric effect on it. This is not the case for the o-substituent or the flexible straight chain compounds. Steric effects such as this will not be apparent in the ionisation of the carboxylic acid, only the ester reaction, so the relationship breaks down.

The above relationship gives rise to a very important equation – the Hammett Equation, which quantifies the LFERs. This is obtained by considering the equation of the straight line plot, which is:

log kx = ρ log Kx + c

where ρ is the slope of the line, and c the intercept. X is the particular m/p substituent in question.

A similar equation can be written where there is no substituent X (i.e. it is H) and this is:

log kH = ρ log KH + c

Subtracting these two equations gives:

log kx – log kH = ρ (log Kx – log KH)

Which can be rewritten:

log kx/kH = ρ log Kx/KH

The Hammett Equation then sets the ionisation of m and p substituted benzoic acids as the standard reference reaction. Knowing KH and Kx for a variety of X-substituted benzoic acids, it is then possible to define a quantity σx as:

σx = log Kx/KH

Where σx is the substituent constant, and its value remains constant for a specific substituent in a specific position, irrespective of the reaction.

This then gives the Hammett Equation –

log kx/kH = ρσx

The reaction constant, ρ, is specific to the type of reaction being looked at. It can be found by the gradient of the linear plot.

Physical Significance of the Substituent Constant:

This measures the electronic properties of the substituent. A positive value indicates electron withdrawing properties, while a negative value indicates electron donation. The magnitude tells us how much of an effect it has. Thus, for something like p-NO2, a large positive value (+0.78) is expected as it mesomerically withdraws electrons via the benzene ring from the opposite benzoic carbon. This is less pronounced for m-NO2 (0.71) because the electrons cannot be mesomerically resonated directly into the NO2 group. Similarly, Cl groups show an even smaller value because they rely on inductive effects only, which are not as powerful in withdrawal.

Conversely, positive values depend on the electron donating strength, so a group such as MeO is more negative than Me when in the para position by the same argument. Note however that MeO in the meta position is electron withdrawing, because the donation cannot be resonated onto the benzoic C from this position, so inductive electron withdrawal is the only electronic effect.

Thus, σx can be regarded as a measure of the overall polar effect exerted by a substituent X on the reaction centre. Its sign indicates the direction. This is compared to the effect of H (set to zero by the definition).

Physical Significance of the Reaction Constant:

This can be seen as the susceptibility of the reaction in question to the effects of the substituent constant.

Thus, for a reaction with a sizeable negative reaction constant, there is typically seen to be a build up of positive charge at or near the reaction centre. The reaction is thus accelerated by electron donating substituents, which help delocalise the positive charge forming in the transition state (and correspondingly retarded by electron withdrawing groups).

Conversely, a positive reaction constant indicates a build up of negative charge at the reaction centre, which is stabilising by electron withdrawal leading to a faster rate.

The magnitude of the reaction constant can be regarded as a measure of the change in charge density at the reaction centre during the Transition State. Thus, it is expected to decrease as the reaction centre is moved further away from the substituent (i.e. by adding carbon groups at the benzylic position – unless these are conjugated with the ring in which case the polar effects can still be transmitted effectively).

Acid Base Catalysis

Catalysis works in general to reduce the ΔG= for the reaction’s transition state, i.e. offer an alternative, lower energy pathway by which to react. Both acids and bases can effect this change on many reactions.

Acid catalysis usually works to make the substrate more electrophilic, while Base catalysis results in the reactant being a better nucleophile to attack this substrate. This can be further sub-divided into General and Specific cases of catalysis.

For general acid/base catalysis, proton transfer occurs in the rate determining step. It is far more common than specific acid/base catalysis, and allows the catalyst to be any acid or base as appropriate.

The rate laws take the form rate = Σ ki [S][Y] where Y is the base or acid as appropriate. An example would be bromination of a ketone.

Specific acid/base catalysis requires that the catalyst is –OH or H3O+ only. An example would be hydrolysis of an epoxide. In this case, proton transfer is very rapid, and forms a pre-equilibrium step (not RDS). Here, rate = kKAS [S][H+].

There are also other possible catalytic routes for acid/base. One such example is nucleophilic catalysis. The difference is that now the attack is on the reaction centre as opposed to a H. There is no proton transfer in the rate determining step. It is highly sensitive to the size of reactant and catalyst. A good example would be Iodo reactions, such as CH3X + I- → CH3I - X +Y → CH3Y - I-. This works because Iodide is both a good nucleophile (displacing X) and a good leaving group (vacating for Y), and thus both steps are accelerated.

Another example of acid/base catalysis would be Lewis Acids and Bases. They work in a similar way to Bronsted Acids/Bases but do not involve protons. Thus, they lower the Activation Energy for the mechanism’s rate determining step.

For example,

Also, Phase Transfer Catalysts exist. They are often cations with several alkyl chains. They work by forming ion pairs with the reagent anion, then move into the Organic phase together. This means the anion has less hydration shells, which reduces the Activation Energy (more reactive). The catalyst must move well between the phases in order to function correctly. This is usually achieved by poor solvation in either phase.

Curtis-Hammett Principle

The Principle states that a product ratio from two interchanging conformers reacting is dependent on both the conformational equilibrium constant and the rate ratios. Therefore the final product ratio can favour the minority conformer if its rate of product formation is high enough.

Take the reaction,

P1 ← C1 ⇌ C2 → P2 with rate constants k1 and k2 as appropriate.

C1 and C2 are conformers in equilibrium.

Derivation,

An example would be something like:

The Hammond Postulate

“If two states occur consecutively in a reaction process, and have nearly the same energy, the interconversion will only involve a small reorganisation of molecular structure.”

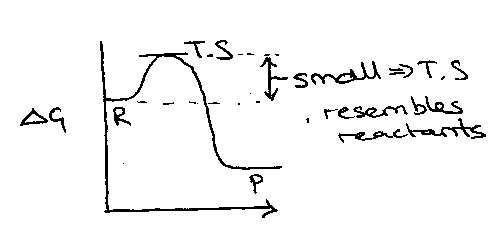
Thus, taking for example an SN2 reaction, if CH3I was attacked by I- there would be a perfectly symmetrical Transition State with properties between the two extremes. However, for the more common asymmetric reaction, the Transition State is going to either closely resemble reactants, products, or some intermediate to both.

Looking now at typical reaction schemes, it can be seen that for a highly exothermic reaction, the Transition State will resemble the starting materials. This is shown by the energy profile:

Conversely, endothermic reactions give Transition States resembling products. Thus, the Transition State is dependent on the relative energies of reactants, products and the transition state itself.

The location of the Transition State leads in turn to selectivity. If the reagent is highly reactive then the Transition State would lie close to the reactant’s energy. Thus, pathways with different Activation Energies cannot be differentiated. With a lower energy reagent, the Transition State will occur later in the reaction profile with a more product-like property. Thus, the pathway with lower Activation Energy will occur more readily.

Principle of Microscopic Reversibility

This relates the forward and backward reactions of a system. It states that all reactions are reversible (but we can’t always measure the reverse). Also, for the reverse reaction occurring at higher temperature, we can guarantee that it occurs by the same mechanism as the forward reaction, i.e. lowest energy pathways are the same in both directions.

Looking at a reaction profile again to explain this:

Marcus Theory

This concerns proton transfer thus:

A-H + B ⇌ A--H--B+ ⇌ A- + H-B+.

i.e. in 3 stages, starting with diffusion of AH and B together, followed by proton transfer, and finishing with A and BH diffusion away.

The free energy of this process implies both intrinsic (internal Energy) and extrinsic (solvent reorganisation energy), and gives the equation:

Kinetic vs. Thermodynamic Control

Consider the following Energy Profile:

EA (P1)        > EA (P2)

k1 > k2

Selective if [P1]/[P2] = k1/k2. This is the definition of kinetic control, where product ratios are entirely governed by rate constants.

However, also considering that:

                         k2     k1

P2 ⇌ R ⇌ P1 (i.e. R now behaving as an intermediate).

                         k-2    k-1

It is now obvious that it is not entirely rate constant based, since reverse reactions have not been considered. The thermodynamic aspect must be examined.

Hence, product ratios are proportional to the difference in Energies of P1 and P2.

[P1]/[P2] = K ln (ΔG(P1) – ΔG(P2)).

Thus, over a long period of time, equilibrium is reached where [P1] > [P2], even though k1 < k2. It is said that P1 is the thermodynamic product, while P2 the kinetic product.

Evidence for Reactive Intermediates

Intermediates can sometimes be detected by either trapping them chemically, or using spectroscopic techniques. This is because the intermediate occupies a “dip” in the energy profile of the reaction, such that moving to backwards or forwards in the reaction requires an energy change.

Identification chemically is often brought about by reacting them with other substrates, indicating that they are stable enough to linger around long enough to react. There are various categories of intermediate, some of which are:

Carbocations – carbons bearing a positive charge. They can be trapped using appropriate anions. They are also often shown to exist in a mechanism due to stereochemical outcomes (since they are planar sp2 hybrids, giving racemisation of product on many occasions).

Carbenes – often react with solvent. Will also react with any suitable substrate added, e.g. adding alkenes gives alkane with dichlorocarbon attachment.

Nitrenes – spectroscopic identification only, but extensively studied.

Arynes – identified by labelling carbons. For example,

pH vs. Rate Profiles

These can be used to determine mechanistically whether acid or base favours or disfavours the reaction, and the mechanism can thus be confirmed.

For example, a reaction to form an imine shows a typical pH / rate profile such as this:

At low pH, Step 1 is rate determining, with rate = k [RNH2][R2CO]. Looking at the mechanism, acid will favour dehydration to remove OH in the second step, but will slow the first step by protonating the amine (making it a far weaker nucleophile). Thus, this fits with the proposed mechanism.

As pH increases, Step 2 is rate determining, with rate = K k2 [RNH2][R2CO][H3O+]. This is because now dehydration is slow since OH is a poor leaving group when not protonated by acid. Since at high pH [H3O+] is slow, the rate law directly shows this is a slow step under these conditions.

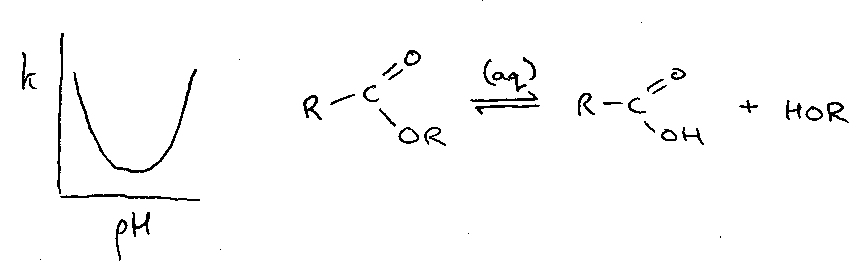
Alternatively, a pH / Rate profile might look like this:

This ester hydrolysis reaction shows the inverse of the above, and the reason is that the reaction is in fact both acid and base catalysed. At low pH, the OR leaving group is protonated to speed this step, while at high pH, H2O converts to –OH, which is a much better Nucleophile for attack.

Unusual pH vs. rate profiles can result. For example, the reactions:

Give rise to the rate profile as shown: