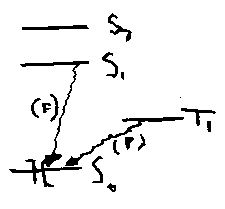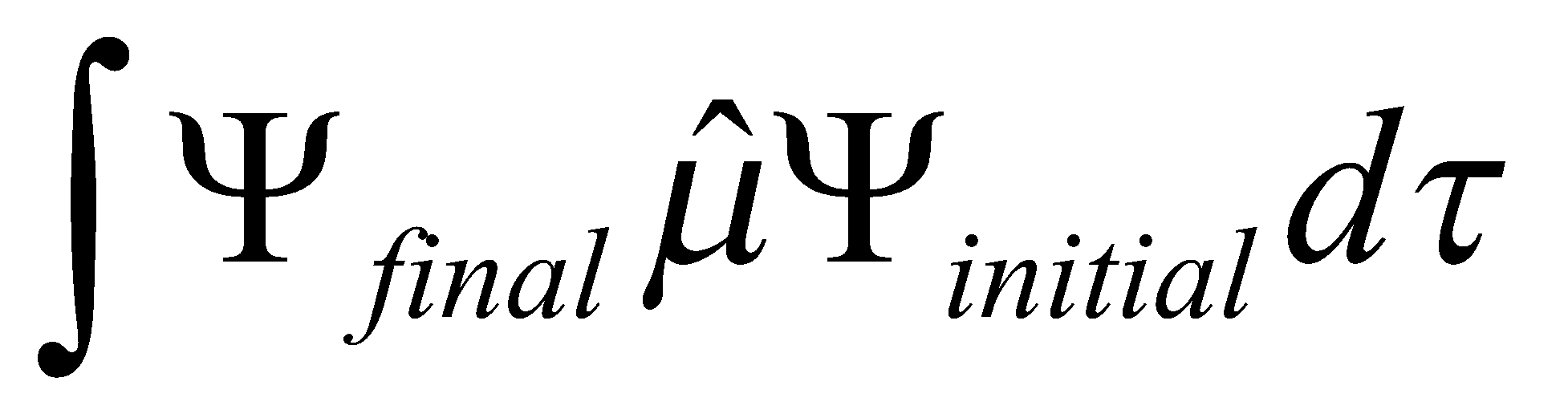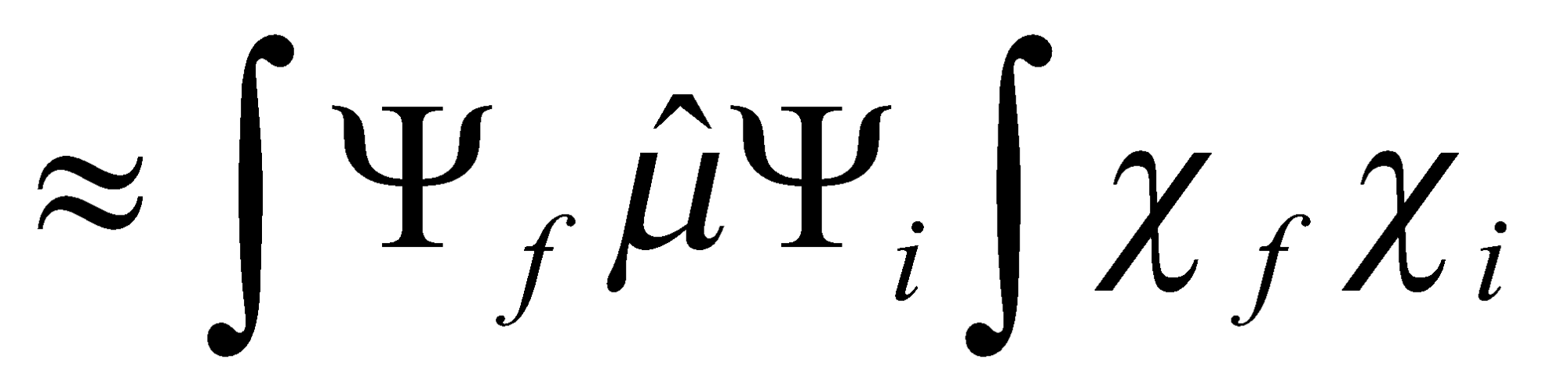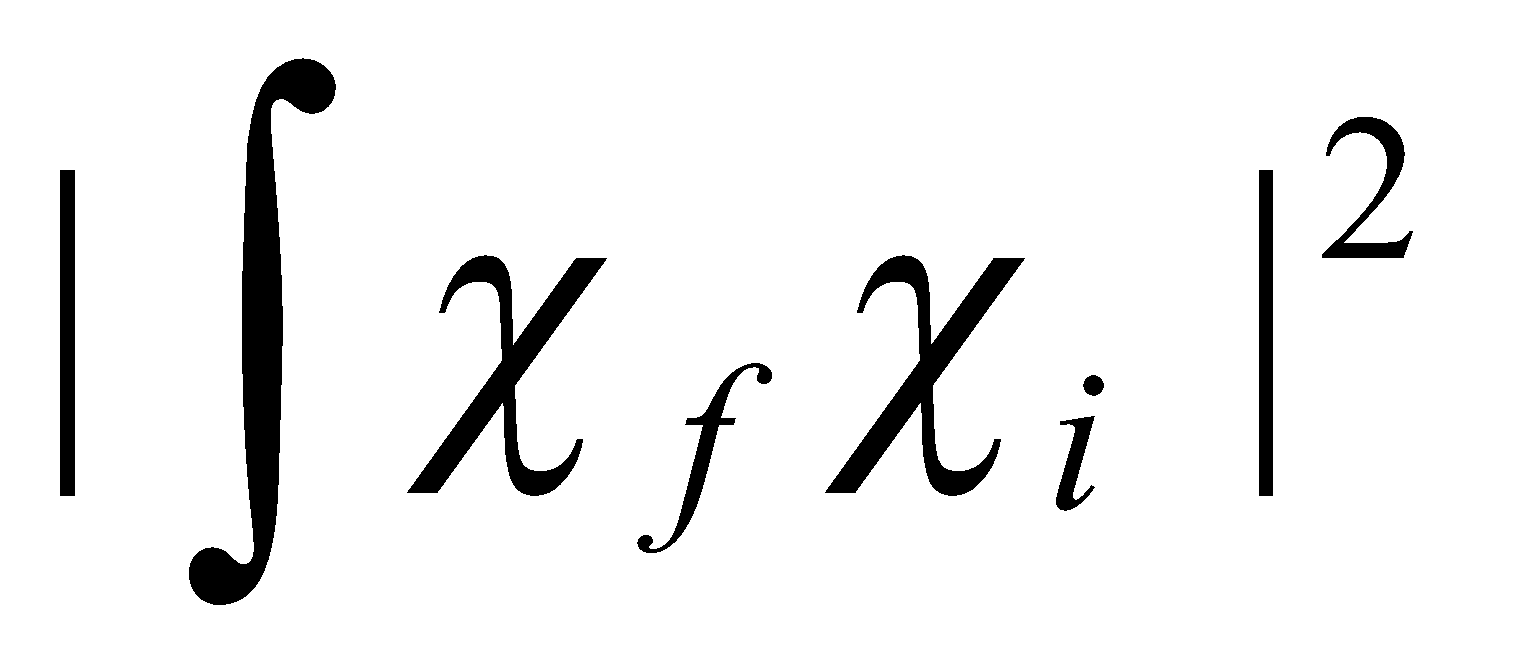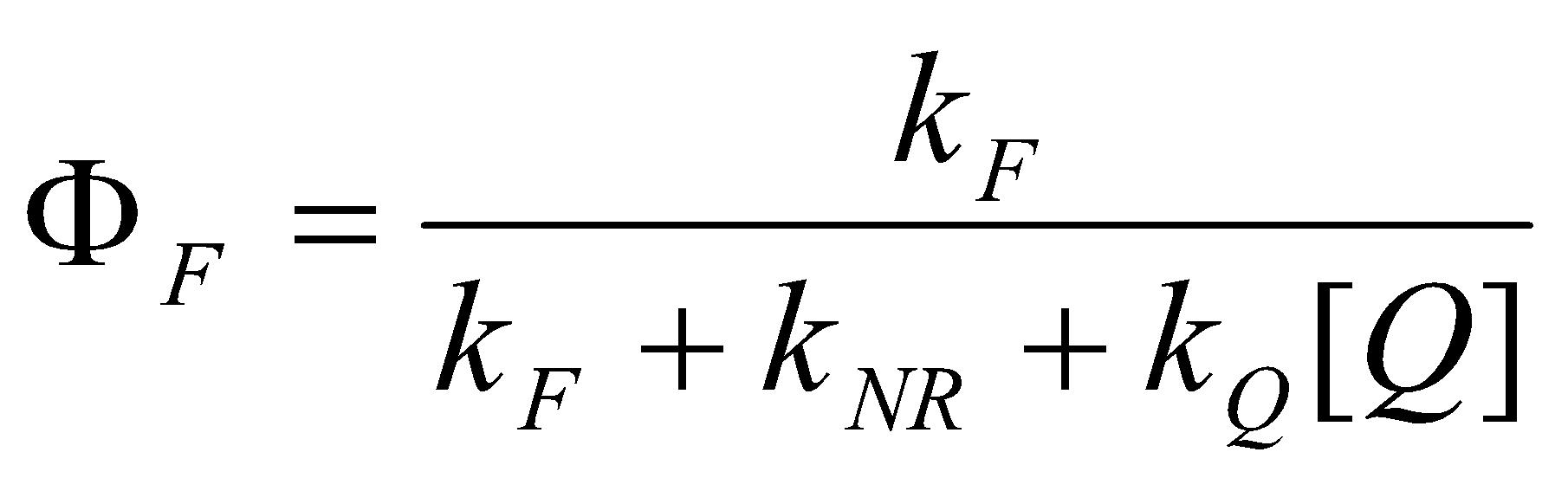Photochemistry Notes

1st Law (Grotthus-Draper Law) – “Only absorbed radiation produces chemical change”.

Exception – inelastic scattering of X- or γ-rays (electronic Raman effect).

2nd Law (Stark-Einstein Law) – “The number of excited molecules produced is equal to the number of quanta absorbed”.

Exceptions – two-photon or multiphoton absorption (lasers).

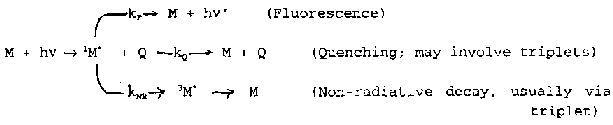
Luminescence

Fluorescence is fast (10-8s). Transition between states of the same spin (ΔS=0).

e.g. many aromatic hydrocarbons and dyes as vapours, in solution, or as solids, at room temperature. “Dayglo” paints. Highlighters.

Phosphorescence is slow (10-3-1s). The transitions are between states of different spin multiplicities, e.g. triplet to singlet (ΔS ≠ 0).

e.g. aromatic hydrocarbons, ketones, heterocyclic compounds in solid matrices at liquid nitrogen temperature. Glowstars.

Exceptions – in heavy atom compounds (e.g. I2) the strong spin-orbit coupling makes the distinction between singlets and triplets invalid. In other words spin-orbit coupling makes spin-changing transitions relatively allowed.

Kinetics of Primary Photochemical Reactions

The steady state hypothesis is always valid for M*:

Rate of change of [M*] = Iabs – kF[M*] – kNR[M*] – kQ[M*][Q] = 0.

[M*] = Iabs { kF + kNR + kQ[Q] }-1

Fluorescence intensity F = kF[M*]

Quantum yield of fluorescence, ΦF = photons emitted / photons absorbed:

ΦF = F/Iabs = kF / { kF + kNR + kQ[Q] }

A similar expression is valid for any primary product.

First-order rate constant for decay of [M*], keff = kF + kNR + kQ[Q]

The measured lifetime in all primary channels is the same, τobs = keff-1

{ τ is the mean lifetime, not half-life. t½ = τ ln 2 }

Hence, ΦF = kFτobs and similarly for all primary products. kF is obtained experimentally by measuring the quantum yield and lifetime.

Radiative Processes

Absorption Strength:

Beer’s Law: I = I0e-α[J]l = I010–ε[J]l

ε = α/ln 10 = molar absorption coefficient, [J] is concentration (mol dm-3), l is length.

Typical values of εmax (dm3 mol-1 cm-1) –

Allowed Transition	103 to 105	Ethene, double bond, π→π*
Symmetry forbidden	1 to 103	Ketones, aldehydes, n→π*
Spin forbidden (1st row)	10-5 to 1	Singlet to triplet absorption in all molecules

Simple form of symmetry selection rule – initial and final state wavefunctions must differ by just one mode (parity change, g↔u).

Spin Selection Rule – initial and final state spin multiplicities must be the same (ΔS = 0).

Emission Strength and Lifetime –

Fluorescence intensity depends on competition:

ΦF = kFτobs

The radiative rate constant (kF = (radiative lifetime)-1) is proportional to the integrated absorption coefficient for transition between the same states. kF is exactly the same as the Einstein A coefficient for spontaneous emission. Einstein proved that there are three radiative processes:

Absorption                         –         rate B [M] [hv]

Spontaneous Emission                 –         rateA [M*]

Stimulated Emission                 –         rate B [M*] [hv]

Stimulated emission is the basis of laser operation. Fluorescence and phosphorescence are forms of spontaneous emission. A practical formula for kF is:

kF (s-1) = 2.88 x 10-9 n2 ( /cm-1)2 ε dv, where n is the refractive index of the solution,  is the average wavenumber, and the integral is taken over the absorption band.

Strong absorption → large kF → chance of strong emission

Weak absorption → small kF → long radiative lifetime → more chance of quenching or internal non-radiative decay.

Examples:

Benzene at 260nm, 1/kF = 414 ns (symmetry forbidden)

Anthracene at 375nm, 1/kF = 14 ns (fully allowed)

Spectra

The shapes of electronic bands depend on vibrational Franck-Condon factors, which are absolute squares of vibrational overlap integrals between the initial and final vibrational levels.

Basic Theory:

Transition probability|μ|2 where μ =

By Born-Oppenheimer separation μ 

Where μ is the electric dipole moment operator, ψ is the electronic wavefunction and χ is the vibrational wavefunction.

So transition probability μelec2F, where F is the Franck-Condon Factor

Semi-classical model

“Vertical” transitions are strongest, because nuclei cannot change their positions or momenta during an electron jump. If there is no change in equilibrium geometry on electronic excitation, Δv = 0 transitions are strongest. If there is a big change (e.g. bonding → antibonding), many vibration levels may be reached giving a broad band.

Examples:

In π→π* transitions such as the first singlet absorption in benzene, a strongly bonding electron goes into an antibonding orbital so there is a significant change in bond lengths and the band is broad with many vibration levels excited.

In n→π* transitions a non-bonding electron goes into an antibonding orbital, but the change in bonding is less so the bands are narrower.

If a non-bonding electron is excited to a highly excited orbital (e.g. a Rydberg orbital) with no bonding properties, the band is essentially a single line showing no vibrational excitation at all.

The shapes of emission spectra (both fluor- and phosphorescence) in liquids are found to be independent of the exciting wavelength and are often mirror images of the corresponding absorption bands.

Exceptions: in molecules which change geometry on excitation (e.g. planar to non-planar), or which react rapidly in the excited state, there is no mirror image relationship.

Observations show:

1. Emission is always from the lowest state of each multiplicity (KASHA Rule)
2. Quantum yields are independent of absorbed wavelength (VAVILOV Rule)

Exceptions – Azulene, thiocarbonyls emit from S2.

3. Emission wavelengths change with changes of solvent.

Explanation – absorption goes from v’’=0 to v’=various. Vibrational relaxation brings all to v’=0 before emission. Franck-Condon factors are similar for (n,0) and (0,n) transitions. Solvation and solvent atmosphere relaxation cause levels to shift after each transition (absorption and emission), and these relaxation processes are much faster than emission.

Excited States

Energy – the energy left in M* = hv – vib. Relaxation (in solution).

Typical bond energies are 350-450kJ mol-1, while one photon at 600nm (red) is equivalent to 200kJ mol-1 but 200nm (ultraviolet) is equivalent to 598kJ mol-1.

Classification – orbital types, in typical E order σ, π, n,  π*, σ* give excitations n→π*, π→π* etc.

Characteristics – the difference between excited states and ground states comes from their Energy, and also e.g. biradical properties (dimerisation), different polarity, acidity, redox properties, equilibrium geometry (C=C), orbital symmetry (pericyclics).

More About Photochemical Reactions

Spin Conservation –

A reaction [AB] → A + B is spin allowed if series |SA + SB|, |SA + SB -1| … |SA - SB| contains SAB.

For example,

1AB → 1A + 1B, 2A + 2B, etc is allowed.

3AB → 1A + 3B, 3A + 3B, etc is allowed.

1AB → 1A + 3B, 2A + 4B, etc is forbidden.

Orbital symmetry has much less effect on a reaction rate than spin, but reactions which can happen on one single potential energy surface, without change of electronic state (“Adiabatic processes”, “homogeneous”) are the most favoured.

Any chemical change, whether light is involved or not, is said to be spin forbidden if ΔS ≠ 0. Because spin is flipped only by a magnetic field, but the fluctuating fields in normal matter are predominantly electric, such processes are generally slow.

Examples:

N2O → N2 (1Σ) + O (3P)	Forbidden
I2 → I(2P) + I (2P)	Allowed
O+ (4S) + H (2S) → H+ (1S) + O (3P)	Allowed
O+ (4S) + CO2 (1Σ) → O2+ (2Π) + CO (1Σ)	Forbidden
O+ (4S) + NO (2Π) → NO+ (1Σ) + O (3P)	Allowed
N2O+ (2Π) → NO+ (1Σ) + N (4S)	Forbidden
H2S+ (2B1) → H2 (1Σ) + S+ (4S)	Forbidden

Note: all the forbidden reactions do happen, but they are generally much slower than allowed ones.

Quenching

Since  and without quencher, and the observed lifetime without quencher τobs = 1/(kF+kNR), it follows that:

F0/F = Φ0/ΦF = 1 = kQ + kQτobs[Q]        [ Stern-Volmer equation ]

Actual fluorescence yields are not needed. If the intensity of fluorescence without quencher divided by its intensity with quencher is plotted against [Q], the slope of the straight line is kQτobs. If the lifetime is known, kQ is determined, or vice versa. Often quenching in solution occurs on every encounter and so is diffusion controlled.

Quenching may involve collision-induced intramolecular energy transfer:

1M* + Q → 3M* + Q [ NB: spin allowed if Q = O2 (3Σg-) ]

Or intermolecular energy transfer:

M* + Q → M + Q*

Excimers (Excited Dimers)

Two molecules may form a bound dimer in the excited state even though they do not bond in the ground state. Pyrene is the classic case.

Py + hv → 1Py* then Normal Fluorescence → Py + hv’

1Py + Py → 1Py2* then excimer fluorescence → [Py2] + hv’’

There is some triplet formation by ISC in pyrene too, and two triplets can pool their energy in the spin-allowed step:

3Py* + 3Py* → 1Py2* → excimer fluorescence

This produces “P-type delayed fluorescence” with a decay rate exactly twice that of the normal triplets.

If [T] = [T]0 exp { -kTt } then [excimer] (formed this way) [T]2 = exp { -2kTt }

Thus the decay of the P-type delayed fluorescence has exactly half the lifetime of the triplet (i.e. the phosphorescence) under the same conditions.

If different molecules are involved in a complex in the excited state, this is called EXCIPLEX.

Non-Radiative Transitions

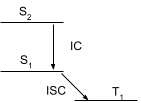
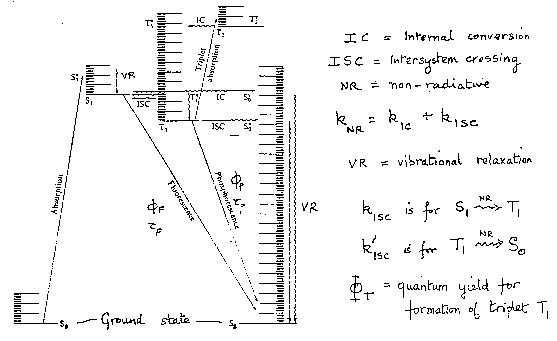
The nature of any luminescence (F or P) and of photochemical reactions depend on the identity of the excited state populated, mainly S1, T1 or S2.

Transitions between electronic states are summarised in the Jablonski diagram:

The type of excited state active in different compounds depends on the rates of the non-radiative transitions, particularly kISC(S1→T1). To determine them, first measure fluorescence quantum yield and lifetime (without quencher) as:

If internal conversion from S1 to S0 is negligible, as is often the case, then ΦF + ΦT = 1 and the intersystem crossing rate kISC(S1→T1) can be determined from the fluorescence lifetime and quantum yield.

If phosphorescence can be observed (usually at liquid nitrogen temperature), and its lifetime and quantum yield are measured, the radiative lifetime for phosphorescence and the intersystem crossing rate constant k’ISC(T1→S0) can be worked out in a similar way.

To determine triplet lifetimes we can also use flash photolysis to obtain relative values of triplet concentration immediately after a flash in solutions with different concentrations of quencher and extrapolate to zero concentration. This can be done at normal temperature.

Summary of Theory:

When IC (S1→S0) can be neglected, all the rate constants can be found by measuring the quantum yields and lifetimes of fluorescence and phosphorescence.

Radiative lifetime,

kF = ΦF / τF

ISC (S1→T1),

kISC = (1-ΦF) / τF

Radiative lifetime,

kP = Φp / (1-ΦF) τp

ISC (T1→S0),

k’ISC = (1 / τp) - kp

Important aspects of the measured rate constants are encapsulated in “El-Sayed’s rules”:

ISC: 1nπ* → 3nπ* and 1ππ* → 3ππ* are slow.

ISC: 1nπ* → 3ππ* and 1ππ* → 3nπ* are fast.

These determine how different classes of molecule behave photochemically, according to the form of their energy level patterns.

e.g. in aromatic ketones, the first medium strength (symmetry forbidden) absorption is to a singlet 1nπ* state, but the lowest triplet state is usually a 3ππ* state. So ISC is fast and the fluorescence yield is near zero, triplet yield is near one and phosphorescence or triplet reactions are observable.

Understanding Non-Radiative Transition Rates

Non-radiative transitions are internal energy transfers. In the large molecule limit their rates follow Fermi’s rule:

kNR = (4π2/h) Hif2ρf

ρf = density of final states (i.e. number of states per unit energy), and Hif = Ψf H ψi .

where Ψ is the total wavefunction (electronic, nuclear, spin), and H is the operator which couples the initial and final states.

For ISC: H is the spin-orbit operator. For IC: H is the nuclear kinetic energy operator (B-O breakdown).

Approximately (mainly B-O) –

kNR = (4π2/h) Hel2ρfF,

where F is a Franck-Condon factor.

HSO has the symmetry of a rotation about one of the axes.

HKE is totally symmetric.

Hence, Hel(ISC) vanishes in this approximation for ISC between states with identical orbital symmetry.

Hel(IC) vanishes except between states of the same symmetry.

The symmetry explains El-Sayed’s rules, but not the differences between kIC(S2→S1) and kIC(S1→S0) or kISC(S1-T1) versus kISC(T1→S0).

For a single, harmonic vibration the Franck-Condon factor can be calculated analytically. The largest arises for the smallest possible change in the number of vibrational quanta, and the rate can be written:

kNR = A Hel2 exp { -BΔE/hvmax }        The Energy Gap Law

where A and B depend only weakly on ΔE or v. The law predicts that in related compounds ln kNR should be a linear function of the energy gaps, as observed, and non-radiative transitions should be slower in deuterated compounds than in hydrogenated ones, as also found. Applied to normal energy level schemes it explains the KASHA, VAVILOV and ERMOLAEV rules. It also explains the exceptional behaviour of azulene (large S1 to S2 gap, small So to S1 gap, so emission (fluorescence) S2→So. Fast IC S1 to S0) and thiocarbonyls (large S2 to S1 gap. S2 = 1ππ* so S2-T2 gap, slow ISC. S1 = nπ* so fast ISC → T1. Hence when absorption is to S1, reaction from T1. Absorption to S2, reaction/emission from S2).