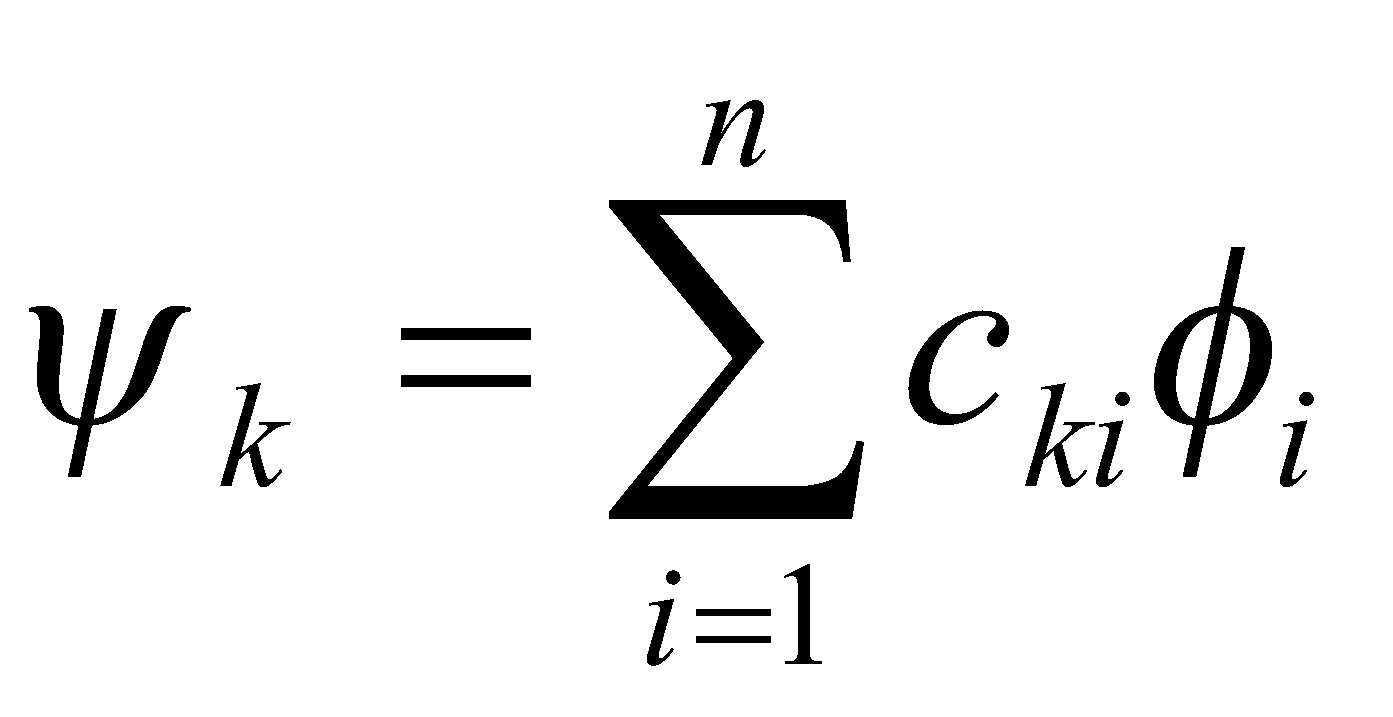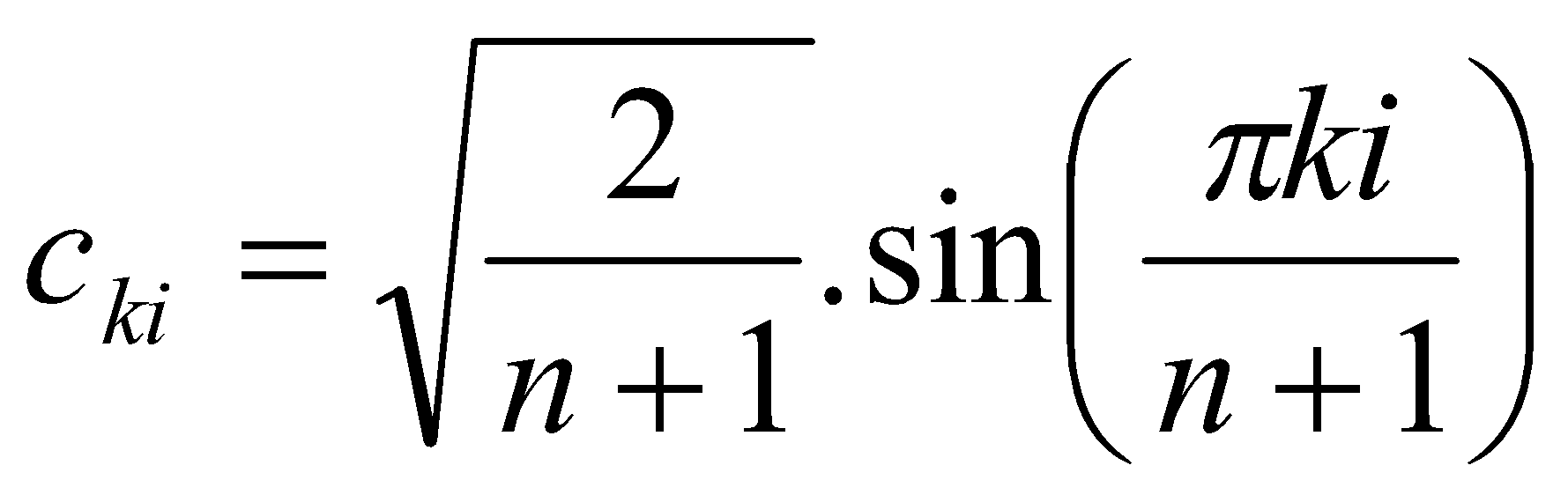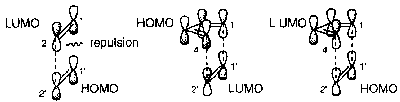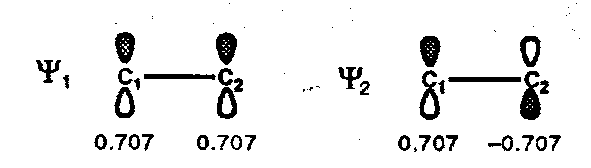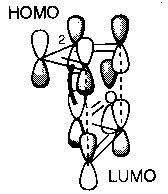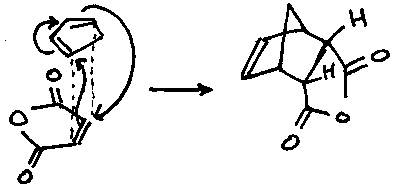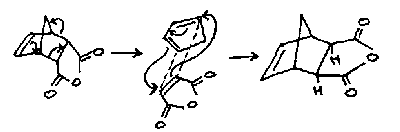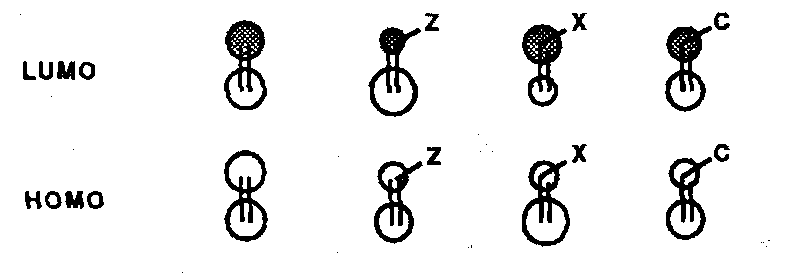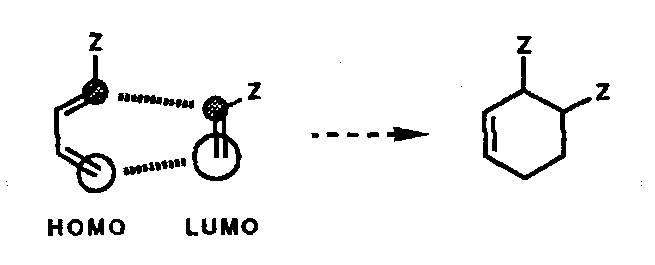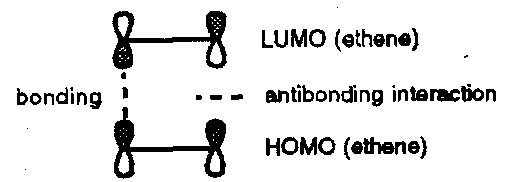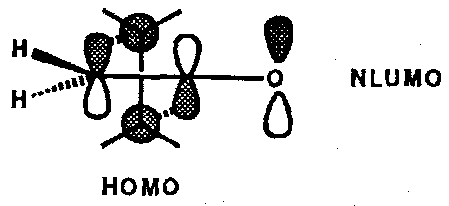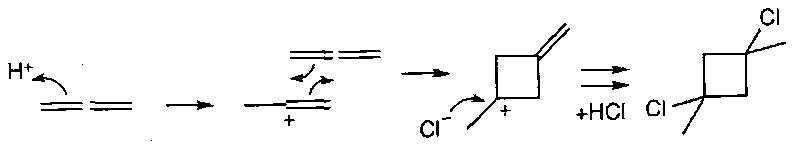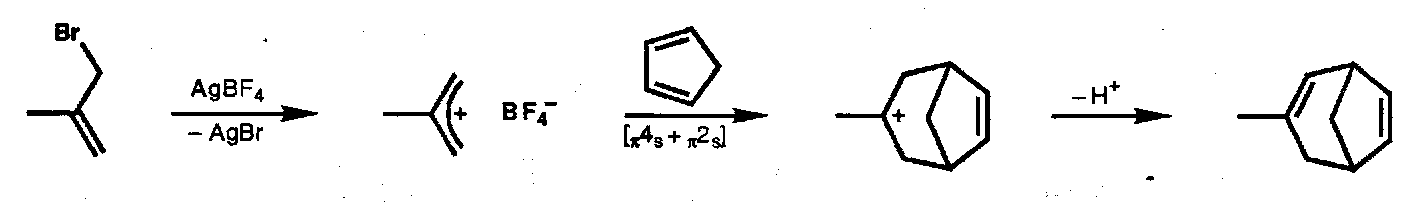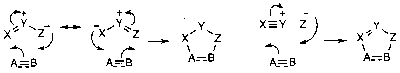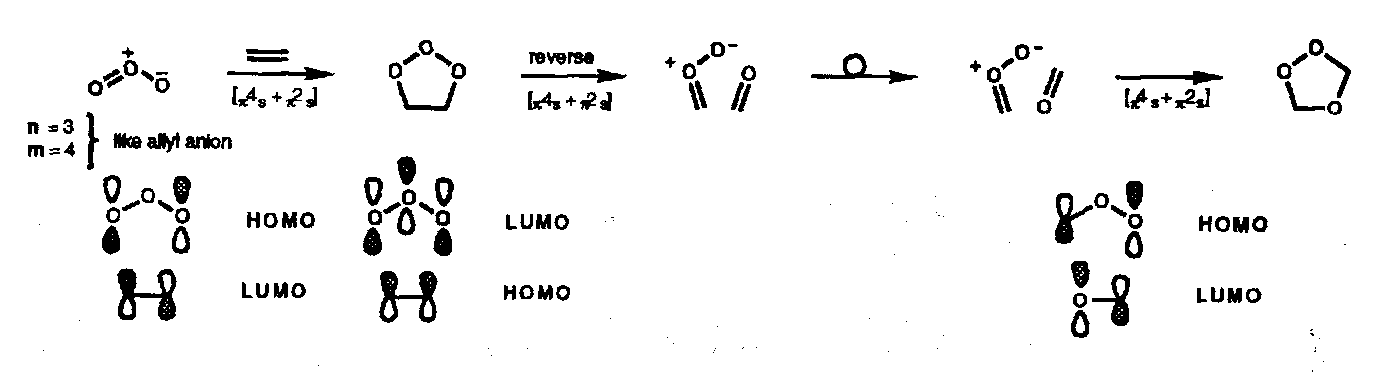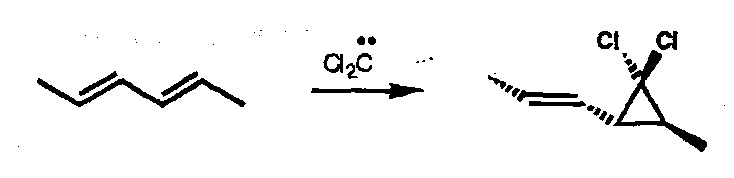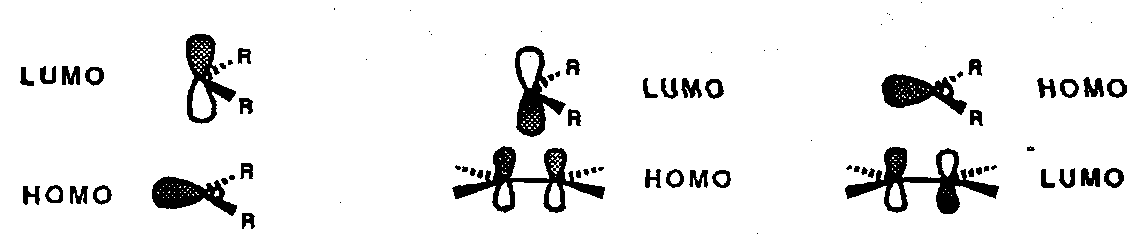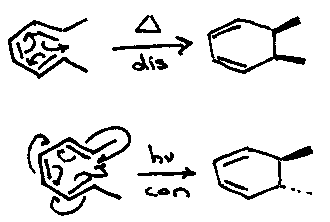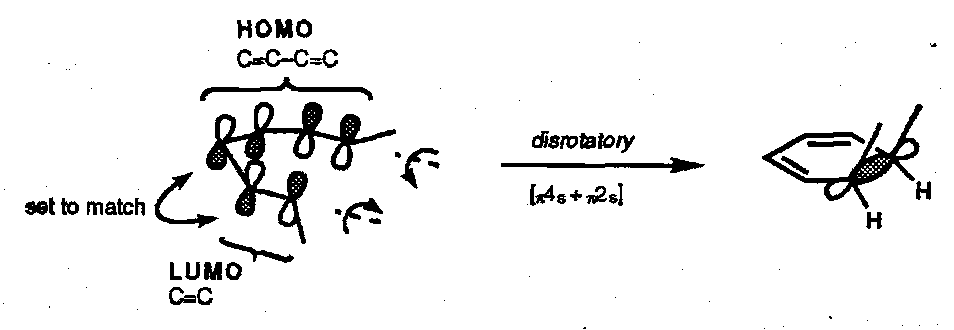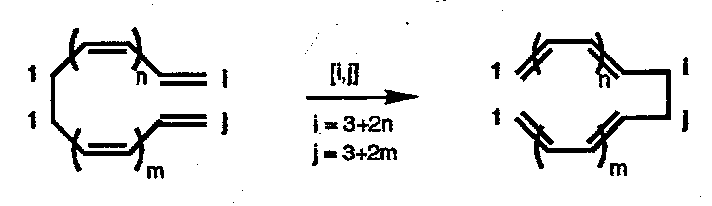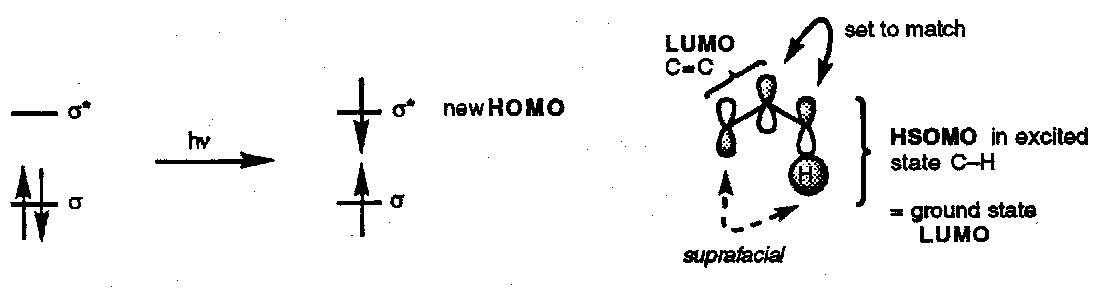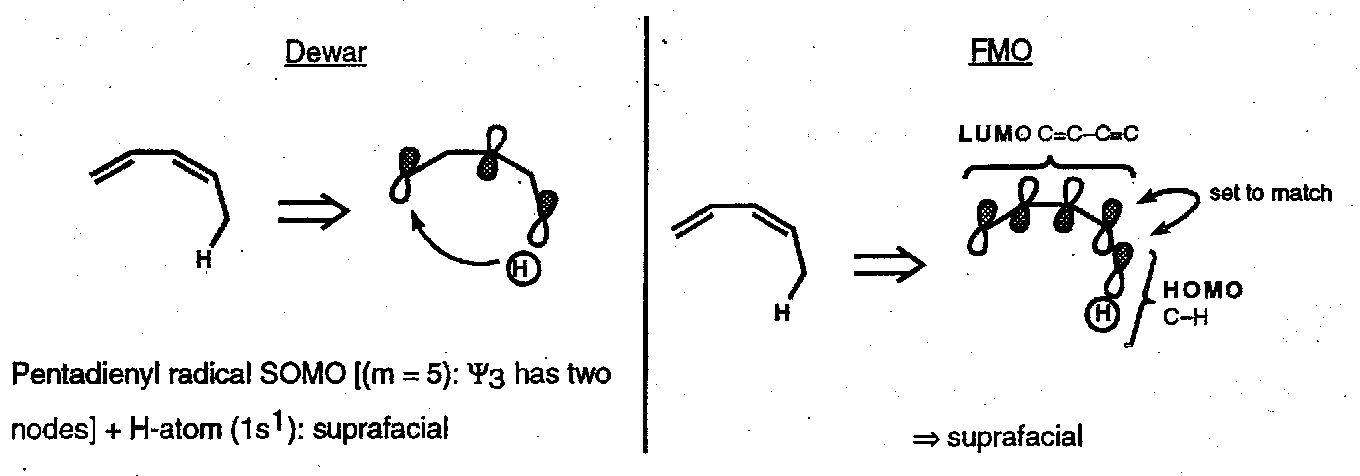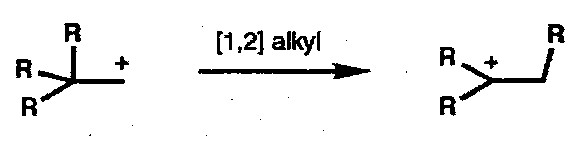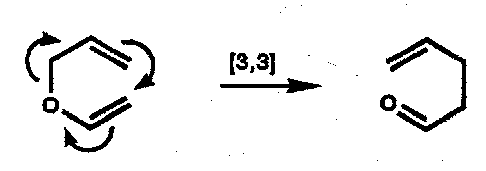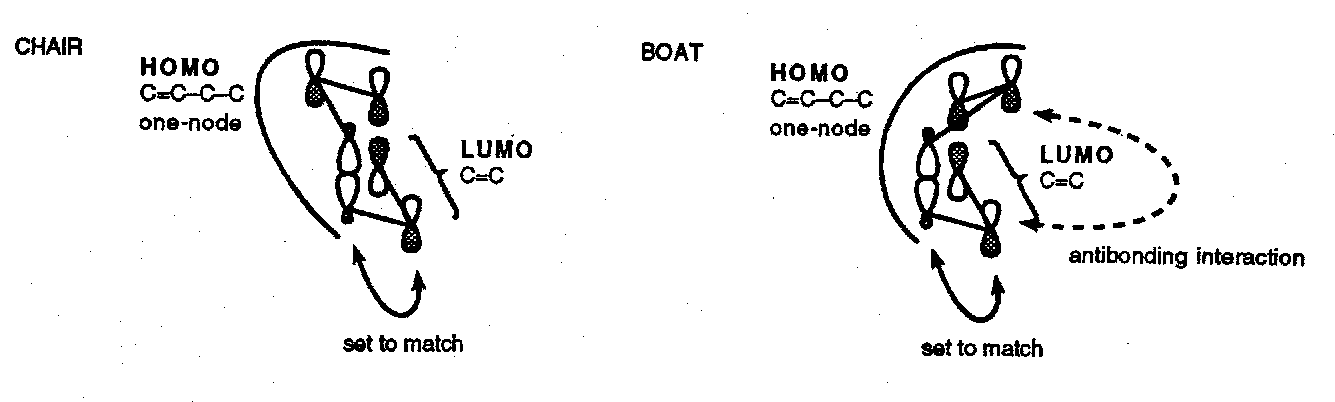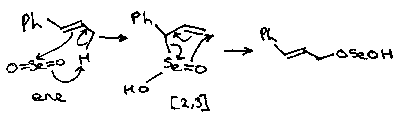Pericyclic Reactions Notes

Pericyclic reactions cannot be treated adequately by “curly-arrow” formalisms and a knowledge of molecular orbital theory is crucial to their understanding.

They are reactions in which “all first order changes in bonding relationships takes place in concert on a closed curve” (Woodward & Hoffmann).

More simply, the term “pericyclic” covers all concerted reactions involving a cyclic flow of electrons through a single transition state.

Pericyclic reactions can be predicted and controlled to a great degree, which makes them very useful in synthesis.

There are broadly four classes of pericyclic reaction:

Sigmatropic –

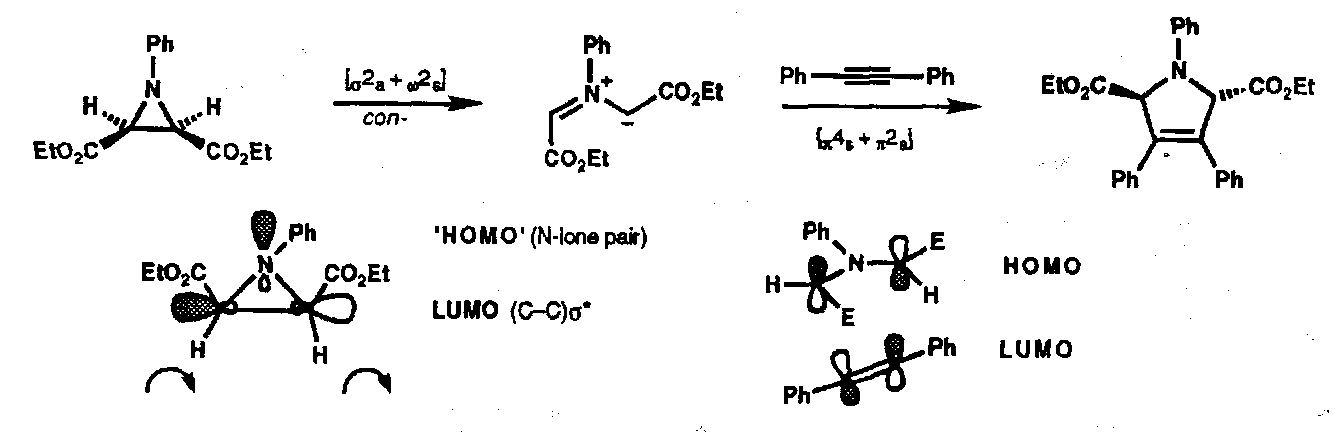
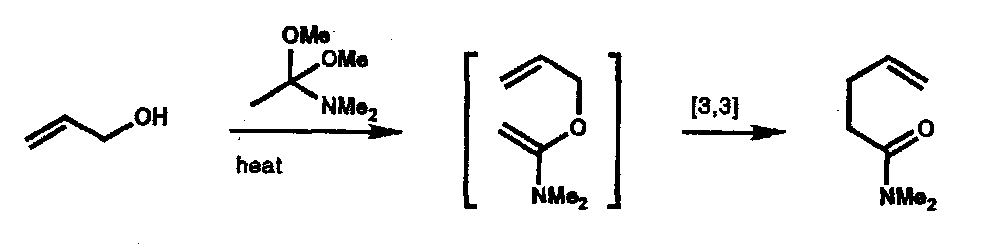
These are unimolecular isomerisations, and involve the movement of a σ-bond from one position to another. An illustration would be the first step of the Claisen Rearrangement:

Note the nomenclature of this reaction, being described as a [i,j] shift. For example, this following is a [1,7] shift:

Electrocyclic –

These are unimolecular. They are characterised by ring opening or closing with a σ-bond forming at one end. Ring closing is more common, since this is formation of a σ-bond at the expense of a π-bond, but ring strain can lead to opening. Two examples are:

Cycloaddition –

This is the largest class of pericyclic reaction. It is characterised by two fragments coming together to form two new σ-bonds in a ring. Some examples are Diels-Alder and Ozonolysis reactions, which are described below.

Chelotropic reactions are a specific type of cycloaddition, where the two bonds are made or broken at the same atom. The classic example of this is carbene addition to a double bond.

Group Transfer –

There are only a few of these reactions, the most common of which is the ene reaction (see further down). They resemble [1,5] sigmatropic shifts, since a σ-bond moves, and they also resemble Diels-Alder, but replacing a π-bond with a σ-bond.

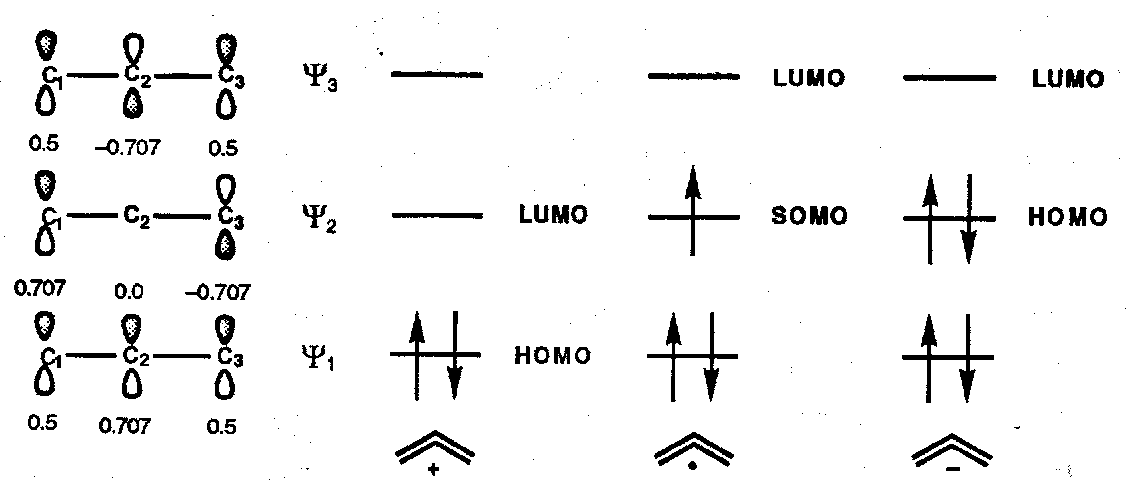
Huckel Molecular Orbitals for Linear π-Systems

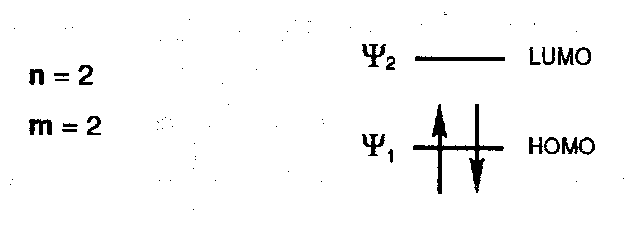
1. Count the contributing p-orbitals. Total = n.
2. Count the electrons held in these orbitals; two for each double bond, two for a carbanion or lone pair, one for an unpaired electron, zero for a carbocation. Total = m.
3. For n contributing p-orbitals there will be n molecular orbitals.
4. Draw n horizontal lines stacked on top of each other to represent the molecular orbitals and feed in the m electrons two at a time from the bottom (lowest energy) up (highest energy).
5. Identify the HOMO, the LUMO, and, for radicals, the SOMO. These are the Frontier Molecular Orbitals (FMOs).
6. Each molecular orbital ψk is considered to be a linear combination of atomic orbitals φi [ where i designates the atom position with the π-system (an integer in the range 1-n) ].

Each atomic orbital is “scaled” by a factor cki which is the coefficient at a particular atom position i within a particular molecular orbital ψk.

For a particular ψk, Σci2 = 1; for a particular atom position i, Σck2 = 1. Evaluated in radians the value of the orbital coefficient is given by the formula:

Aromatic Transition State 

All thermally induced pericyclic reactions have transition structures involving a total of 4n+2 electrons. This explanation in terms of an aromatic transition state can be extended to cover all situations (including those involving antarafacial thermal reactions) using Frontier Orbitals.

Frontier Molecular Orbitals

These are the HOMO of one component and LUMO of the other.

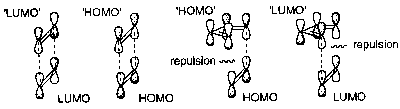
Compare the following:

The diagram on the left shows a [2+2] addition – not allowed due to the repulsion (antibonding effects of opposite sign of wavefunction). The other two show a [4+2] addition (the difference is the LUMO and HOMO are reversed – still both allowed). Note that barrier to [2+2] addition is only present when both bonds are trying to form at the same time – stepwise is allowed, but not pericyclic.

An alternative would be for the upper lobe of the C1 in the [2+2] addition to interact. This would represent an antarafacial reaction, which is allowed. However, this requires a long flexible conjugated chain.

From a photochemical viewpoint, one molecule has an electron promoted from HOMO to LUMO, and this excited state molecule reacts with a molecule in the ground state. The excited LUMO may react with the LUMO of the ground state molecule, or the excited HOMO with the ground state HOMO. Both of these are the lowest energy transition states, and can be depicted as ends of the [2+2] addition and it is thus allowed photochemically.

This can be shown in the following diagram, where the pair on the left represent a [2+2] addition and the pair on the right a [4+2]:

Frontier Orbital Theory is however only of any use for selectivity and small differences in reactivity. It is also inherently bimolecular. Thus, for unimolecular sigmatropic and electrocyclic reactions it is no use, nor does it explain why the barrier to forbidden reactions is so high.

π-MOs for Ethene

• calculate cki at each position within ψ1 and ψ2 (c11, c12 and c21, c22)
• represent this as a picture showing p-orbitals with the upper lobe shaded where the coefficients are positive and with the lower lobe shaded at positions with negative coefficients. This gives a representation of the relative phase properties of the atomic orbitals contributing to a particular MO.

• the HOMO of ethene (π) has no sign inversions (no nodes), the LUMO (π*) has one node.

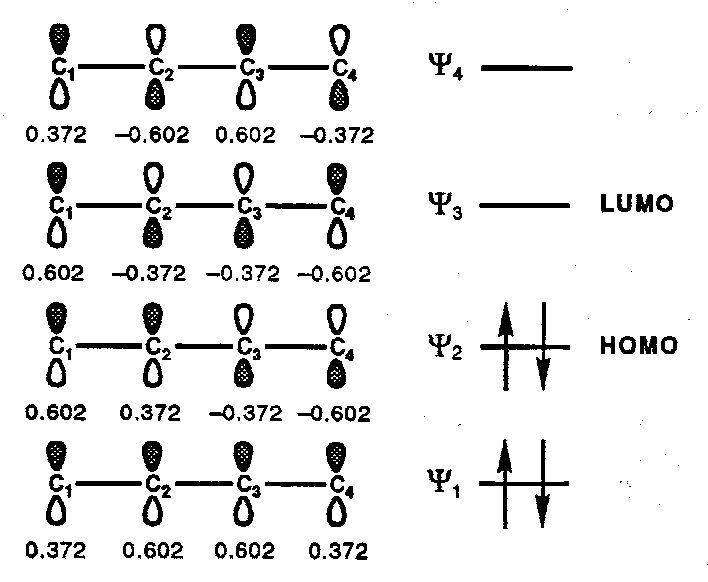
π-MOs for 1,3-Butadiene (n=4, m=4)

The number of nodes increases by one on going to the next higher MO and, in general, the number of nodes within a particular MO (ψk) is k-1. In a linear π-system if the number of nodes is Even then the terminal orbital coefficients will be of Equal sign (i.e. both positive or both negative); if the number of nodes is Odd the terminal coefficients will be of Opposite sign.

π-MOs for Allyl Systems [n=3, m=2 (cation), 3 (radical), 4 (carbanion) ]

Orbital Symmetry Control in Electrocyclic Ring Opening of Cyclobutenes

• consider the p-orbitals that comprise the σ-bond as this bond breaks; there are two modes of rotation of the methyl groups as the reaction proceeds (neglect the possibility of the two methyl groups swinging towards each other).
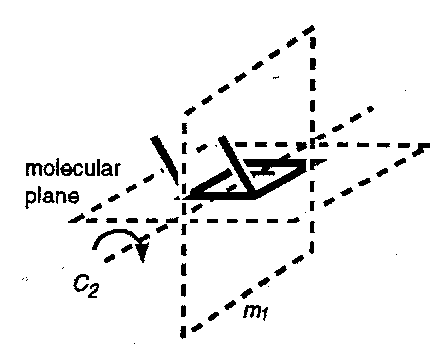
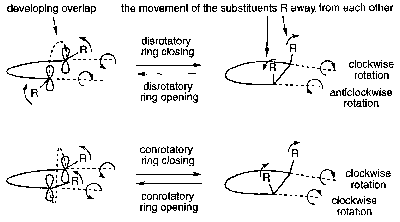
• In the first case both the bonds rotate in the same direction; this is conrotatory ring opening. Throughout this process the molecule retains a two-fold axis of rotation (the axis passes through the plane of the molecule and through the breaking σ-bond).

• in the second case the bonds rotate in opposite directions – disrotatory ring opening – and the molecule retains a plane of symmetry throughout (the plane is perpendicular to the plane of the molecule and passes through the breaking σ-bond).

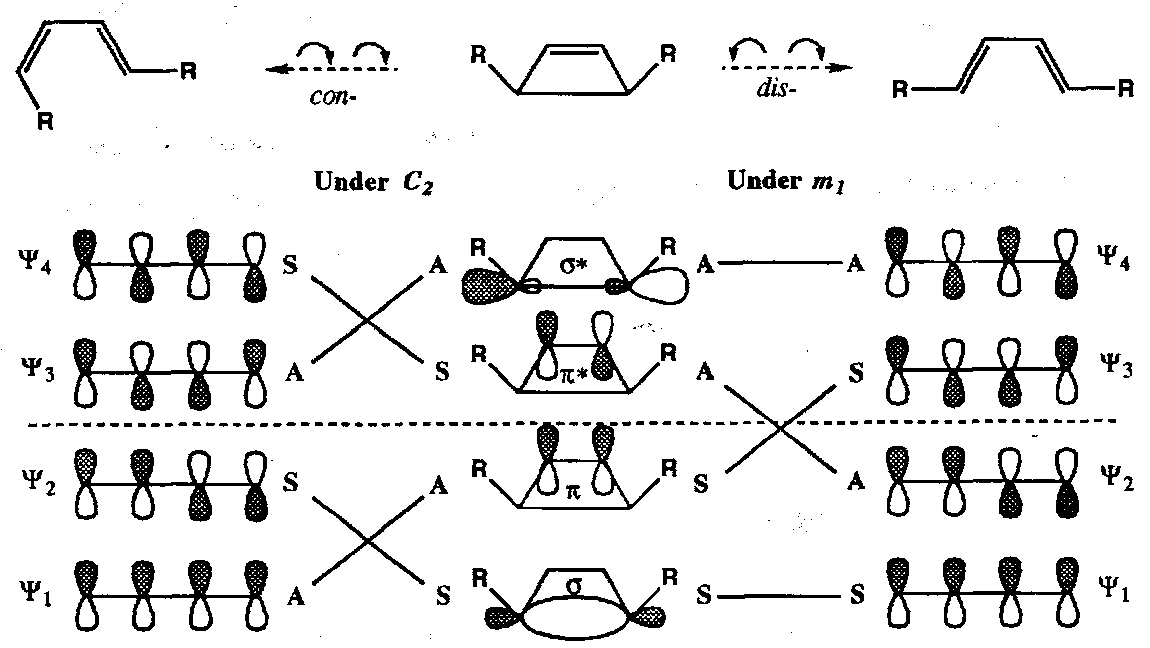
The orbitals directly-involved in the cyclobutene and butadiene product are designated as symmetric (S) or antisymmetric (A) with respect to these symmetry operations; rotation about C2 for the conrotatory case and reflection in m1 in the disrotatory case. Orbitals of like symmetry are then correlated with one another, as follows.

Correlation Diagrams

Correlation Diagram for Electrocyclic Ring Opening of Cyclobutenes

In the conrotatory mode all bonding orbitals in the cyclobutene correlate with bonding orbitals of the diene; this is thermally allowed (“favoured” is a better term). In the disrotatory mode one of the bonding orbitals correlates with an anti-bonding orbital; this is thermally forbidden (“disfavoured”).

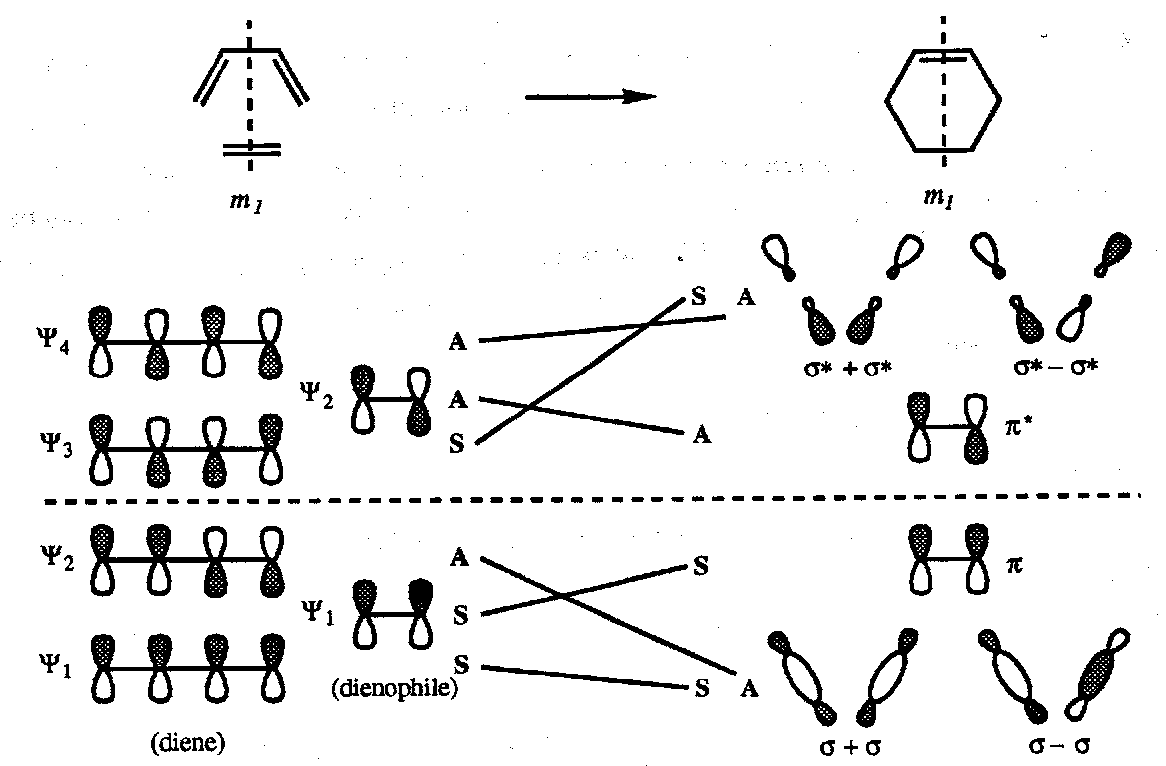
Correlation Diagram for the Diels-Alder Reaction

In this reaction a plane of symmetry m1 is preserved throughout the process (perpendicular to the molecular planes of both diene and dienophiles and passing through the double bond of the dienophiles and the central single bond of the diene) therefore the orbitals are designated S or A after reflection in this plane. In the product there are two new equivalent σ-bonds which are not proper symmetry combinations with respect to the plane m1; they have therefore to be taken as σ1 + σ2 and σ1 - σ2 combinations as shown:

Thus all the bonding orbitals are correlated with bonding orbitals, all the antibonding orbitals correlate with antibonding. Thermally allowed.

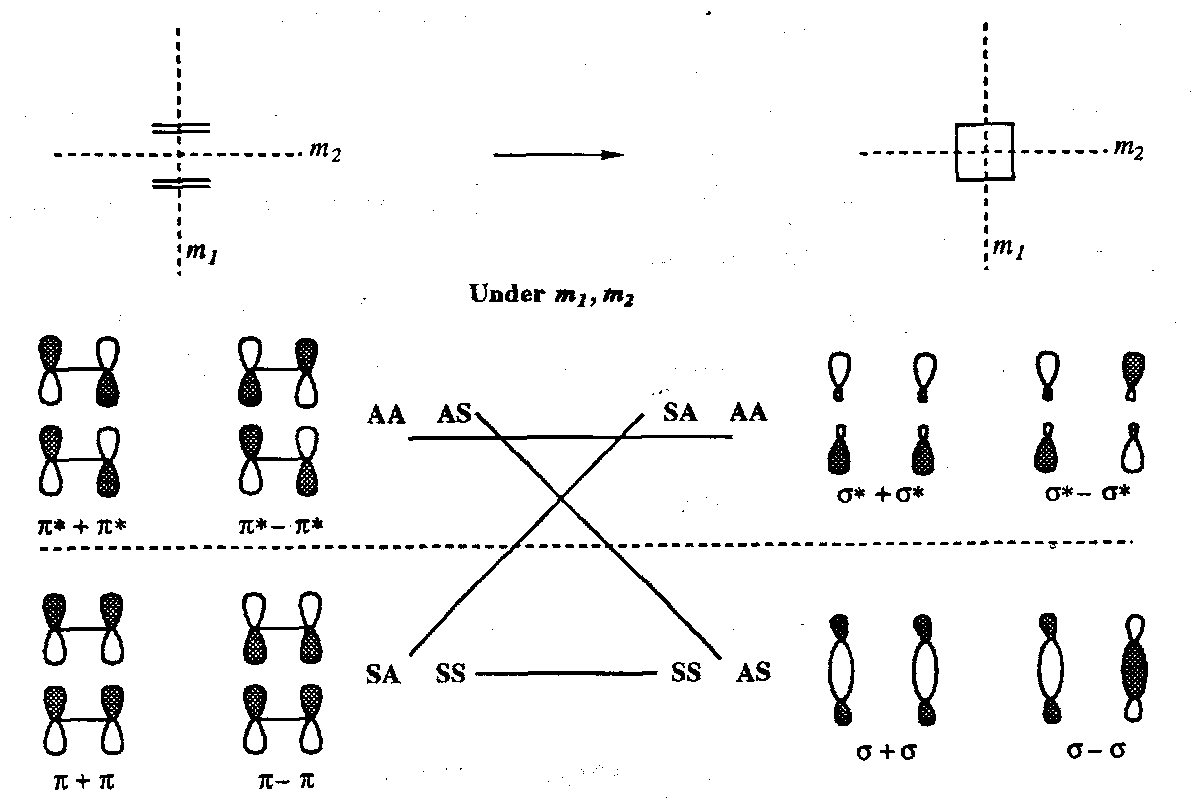
Correlation Diagram for Alkene Dimerisation

The natural (thermal) approach for [2+2] cycloaddition (one double bond stacking directly on top of the other) is disallowed since there is cross-correlation between bonding and antibonding orbitals. Note again the use of orbital combinations with equivalent pairs and that there are two planes of symmetry throughout the process:

Perturbation Methods and Frontier Orbital Treatments

• Allow easier practical prediction and understanding of pericyclic processes but it must not be forgotten that these are equivalent (although less rigorous) statements of the requirements of orbital symmetry and state correlation.
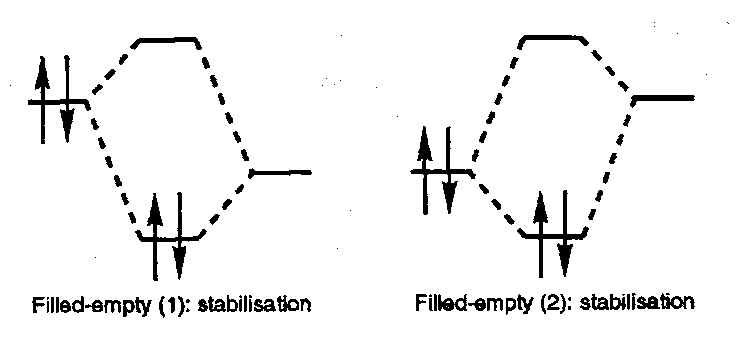
• The most important interaction between two molecules or molecular components is that between empty orbitals in one component and filled orbitals in the other.

For thermal reactions the significant interactions are as shown:

Component A	Component B
Unoccupied MO	Unoccupied MO
Occupied MO	Occupied MO

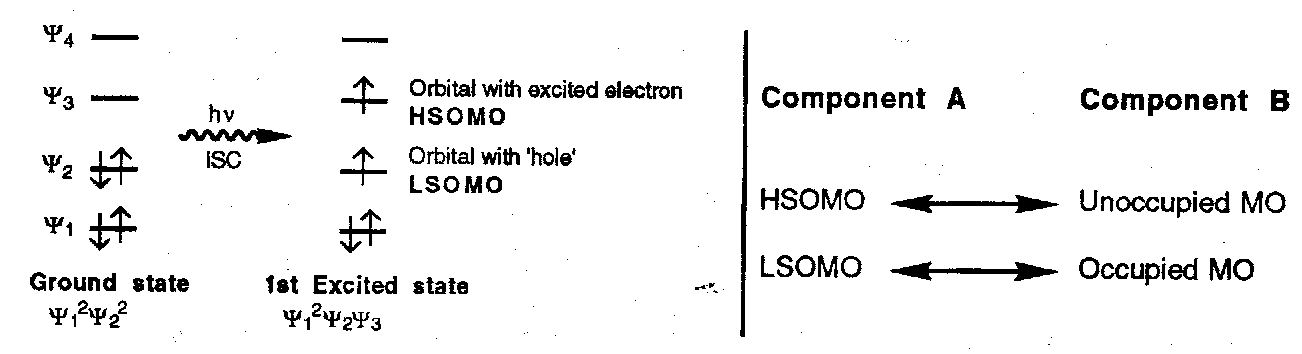
For photochemical reactions in which one molecular component (A) has been excited:

• When the occupied MOs in one component lie lower in energy than the unoccupied MOs in the second component (the usual situation) the stabilising interaction will be greater when these orbitals are closer in energy; this implies that the dominant interactions will be between the FMOs, i.e. the HOMO, the LUMO, the LSOMO, and the HSOMO as follows:

Thermal Reactions	HOMOA ↔ LUMOB
	LUMOA ↔ HOMOB
Photochemical Reactions	HSOMOA ↔ LUMOB
	LSOMOA ↔ HOMOB

• The interacting orbitals must possess phase properties that allow only bonding interactions; overlap of opposite orbital phases is antibonding and unfavourable.

Woodward-Hoffmann Rules

1. A ground state pericyclic change is symmetry-allowed when the total number of (4q+2)s and (4r)a components is odd.
2. A photochemical pericyclic change is symmetry-allowed when the total number of (4q+2)s and (4r)a components is even.

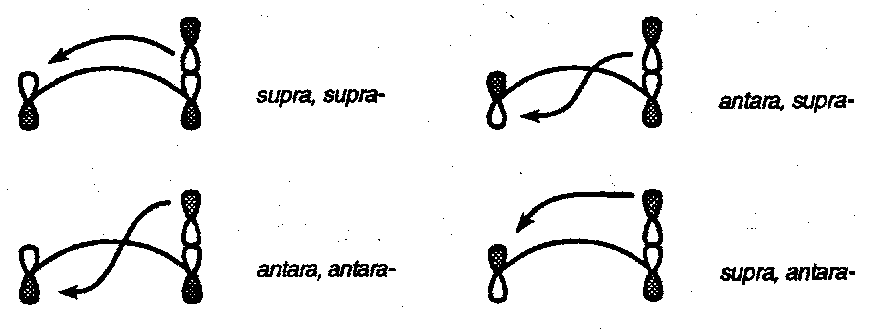
q and r are integers and the subscripts s and a denote suprafacial and antarafacial respectively.

The components of the cycloaddition are obviously the two separate electron systems (molecules) coming together. Looking at these components, we have to then consider:

1. How many electrons?
2. Suprafacial or antarafacial?
3. Which can be expressed as 4q+2 and which as 4r?

Definitions

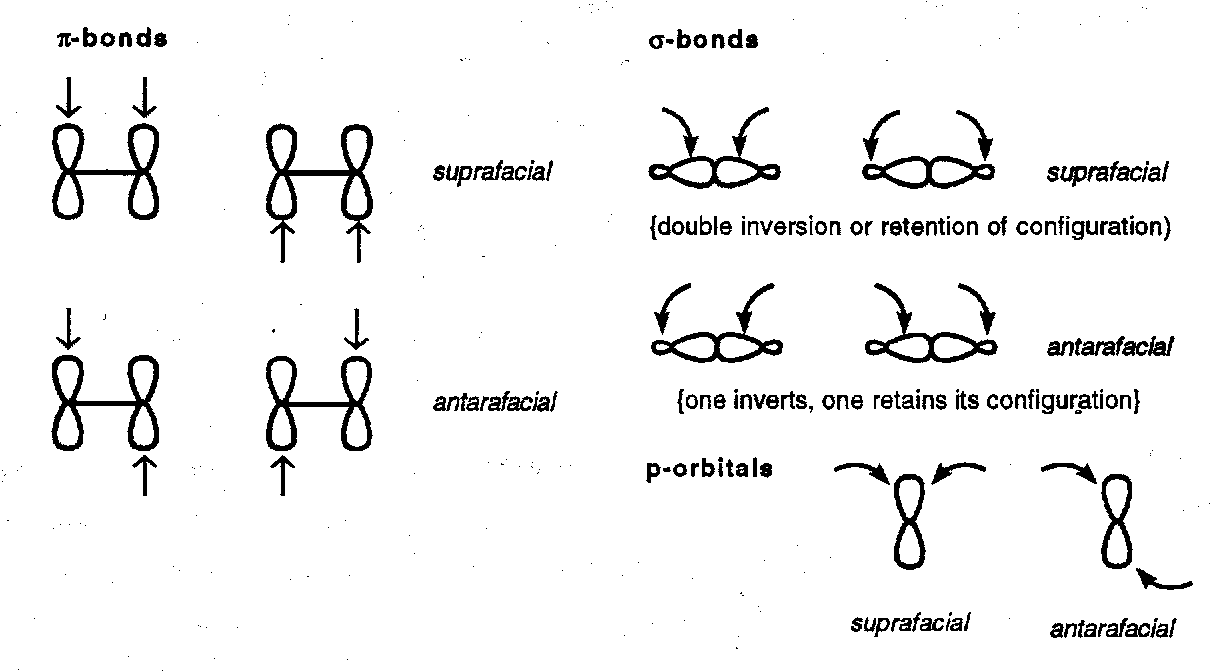
Suprafacial and antarafacial refer to modes of bond formation that are respectively on the same face and on opposite faces of a molecular component.

Because an s-orbital has no nodal properties all its reaction modes are suprafacial.

For example, the Diels-Alder has two components, one of 4 electrons and one of 2. They both undergo reaction in a suprafacial sense. The diene, with 4 electrons, can be expressed as 4r, and the dienophile can be expressed as 4q+2 (q=0).

Thus, the total components that are (4q+2)s and (4r)a is 1, because there are (4q+2)s and (4r)s only. Thus Diels-Alder is symmetry allowed thermally (which we knew). It is typically described as a [4s+2s] cycloaddition as established. This can be further enhanced by describing the location of the electrons in question – both π orbitals in this case, so the reaction becomes [π4s + π2s].

Note also that by considering the diene as two separate individual alkenes instead, the description then becomes [2s+2s+2s], but the W-H Rule still shows it is allowed.

One final piece of notation: when an atomic orbital is a significant component of a pericyclic process the symbol ω is used to designate this.

Cycloadditions

Two or more molecules or molecular components (from now on, “components”) react together to form two or more bonds in a new ring.

It should be noted for a sense of completeness that not all cycloadditions are pericyclic, and that they can occur in a stepwise manner. This allows the selection rules to be broken (i.e. [2+2] additions etc. can occur). The reactions can be made stepwise by equipping one reagent with a powerful electron-donating group (nucleophilic) and the other with a powerful electron withdrawing group (electrophilic).

In assigning a cycloaddition to a class we assign descriptors π-, σ- or ω- to the electrons directly involved in the process (i.e. those that move when curly arrows are drawn), count how many electrons are involved in each component, and identify whether the components are reacting in suprafacial (s) or antarafacial (a) modes.

Allowed and Forbidden Cycloadditions

Not all cycloaddition reactions are allowed. For example, [2+2] reactions are not. This is due to a kinetic barrier to reaction (2 alkenes forming a 4 membered ring is thermodynamically favourable, but kinetically impossible).

Generally, a thermal pericyclic reaction is allowed if the number of electrons involved can be expressed as 4n+2. 4n is forbidden. Crudely, an odd number of curly arrows is allowed while an even number is forbidden.

Conversely, photochemical pericyclic reactions are allowed if the number of electrons is 4n, but not if it is 4n+2. Note though that when putting that much energy into a reaction, other mechanisms may take precedence.

Diels-Alder Reaction

Constructive overlap is complete whichever way round we take the HOMO and LUMO interactions. The reaction is suprafacial with respect to both components, therefore it is a [π4s + π2s] cycloaddition and is thermally allowed by the W-H Rules (and photochemically disallowed) as mentioned earlier.

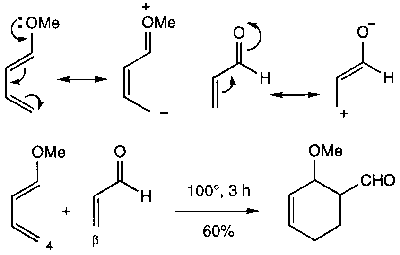
The reaction above would be very, very slow however. Electron-donating groups on the diene and electron-withdrawing groups on the dienophile greatly accelerate it. Also, the more powerful the electron-donating or withdrawing substituents, the more regioselective the reaction (see below).

Note that the diene must have the cis conformation to react – a trans diene would lead to a trans double bond forming in a ring, which is too high in energy to occur.

As with all pericyclic reactions, the path is determined by thermodynamics. Thus, studying the reverse retro-Diels-Alder reaction can often make determining the product easier.

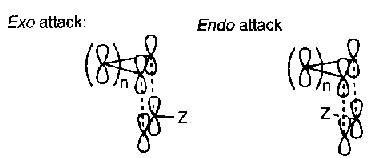
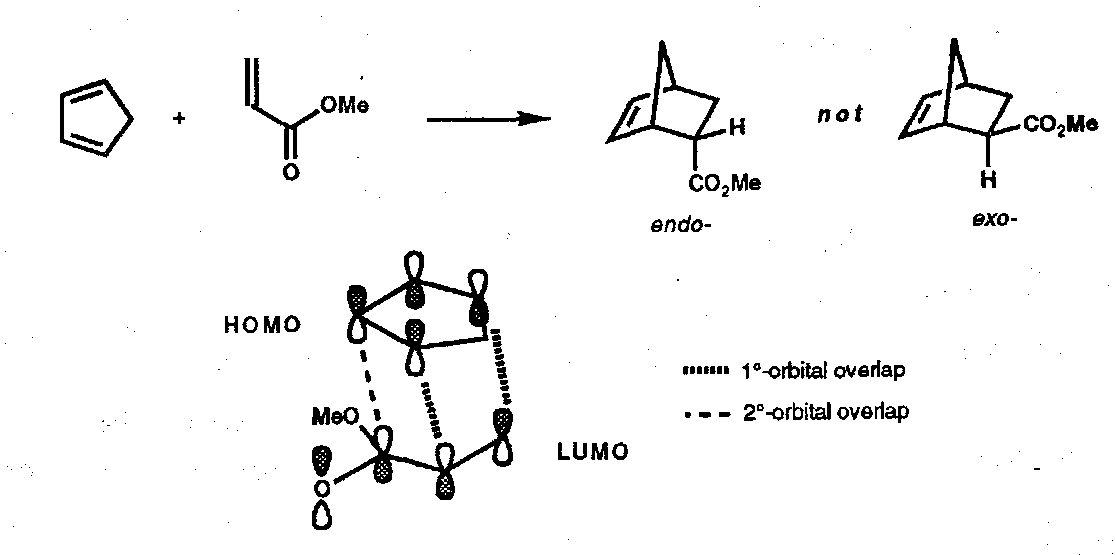
Stereoselectivity

There are two possible ways of attacking suprafacially, and these are described as ENDO and EXO. This usually governs speed of the reaction (since both are allowed by the rules above) and is affected mostly by substituents present. The two approaches can be illustrated:

The favoured transition structures are those with electron-withdrawing substituents in the more hindered environment, but these are thermodynamically less favoured. This can be explained by looking at the Frontier Orbital approach, best depicted as:

The bold line shows an additional bonding interaction in the endo form which favours this route.

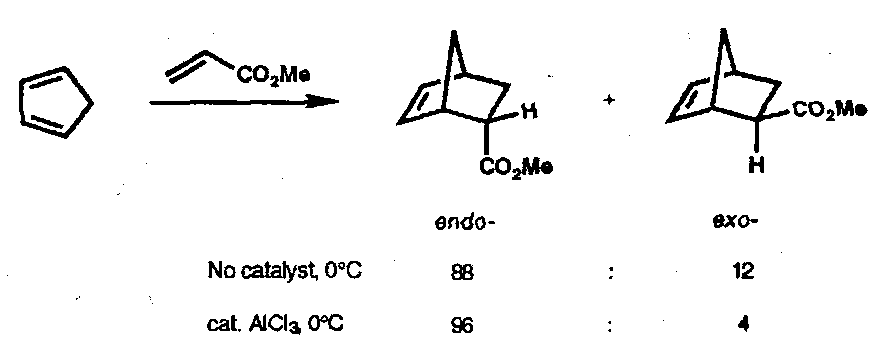
This leads to kinetic vs. thermodynamic control, depending on conditions. For example, the endo rule would suggest that at 0oC in ether:

However, refluxing in THF leads to further reaction of the above product, first by retro-Diels-Alder and then re-addition to form the thermodynamic product:

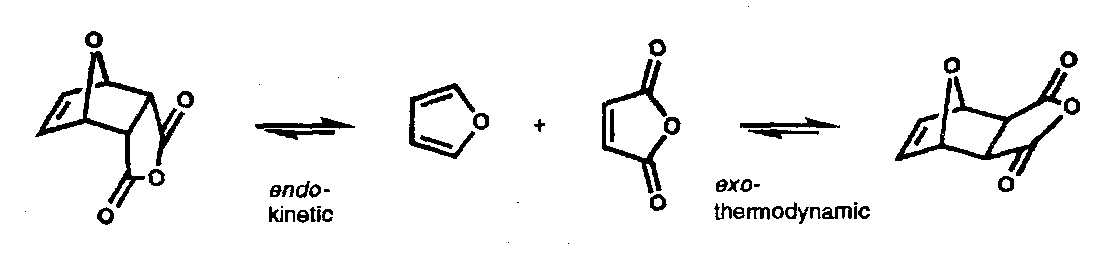
Endo-Selectivity

The preference for kinetic formation of the endo- adduct (which is less stable than the exo- adduct) has been described deceptively convincingly by “secondary orbital overlap”. This is a stabilising interaction of in-phase orbitals in the transition state that does not lead to new bonds. In cases where the reaction readily reverses – for example with stable dienes such as furans – the thermodynamically preferred exo- adducts are usually obtained.

There is not a great deal of evidence for this in general; high-level ab initio molecular orbital calculations have been unable to detect such effects. It is likely that charge transfer from the nucleophilic diene to the electrophilic dienophiles leads to the possibility for maximum Coulombic interaction when the electronegative activating group is folded under the diene. This is still a matter of debate.

1,3 dipolar cycloadditions (see below) tend to show a much lower degree of endo/exo stereoselectivity.

Regioselectivity

This applies when the dienes or dienophiles are unsymmetric. The outcome can usually be predicted by considering an extreme case of mechanism, where resonance puts a negative charge on one end of the diene, and positive charge on one end of the dienophile. Thus,

The above does not constitute a hard and fast rule, however, since Woodward-Hoffmann rules must be considered.

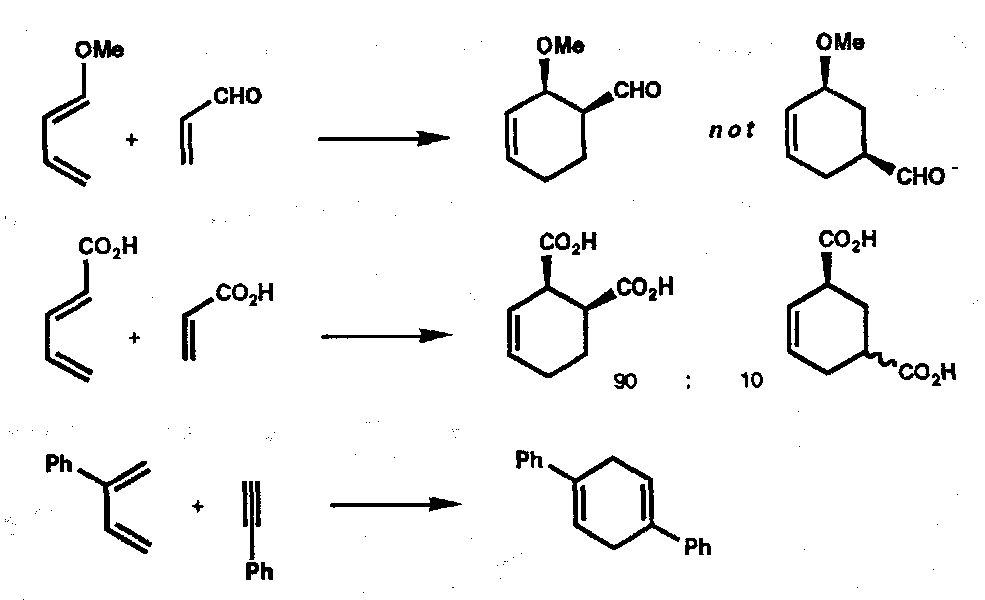
Also, “ortho” and “para” products tend to dominate in Diels-Alder reactions:

The first example might be expected (on arrow-pushing grounds) but in the less obvious cases knowledge of the orbital coefficients, cki, at the atoms to which new bonds are made is important. Orbital interaction (and hence transition state stabilisation) is maximised when large orbital coefficients pair (leaving the two smaller coefficients to pair), i.e. Large-Large + Small-Small > Large-Small + Small-Large. Generalising:

Energies

1. Electron withdrawing groups (Z, e.g. carbonyl) lower both the HOMO and LUMO.
2. Electron donating groups (X, e.g. methoxy) raise both the HOMO and LUMO.
3. Merely conjugating groups that do not significantly withdraw or donate electron density (C, e.g. C=C, Ph) raise the HOMO and lower the LUMO, i.e. they reduce the HOMO-LUMO gap.

Coefficients

Qualitative pictures of the dienophiles (derived from experiment and theoretical combinations of ideal substituents) depict top views of the π-system with larger circles representing larger coefficients.

• in all substituted cases the coefficient on the β-carbon is larger in the HOMO; in the LUMO the β coefficient is larger for Z and C cases, smaller for X cases.

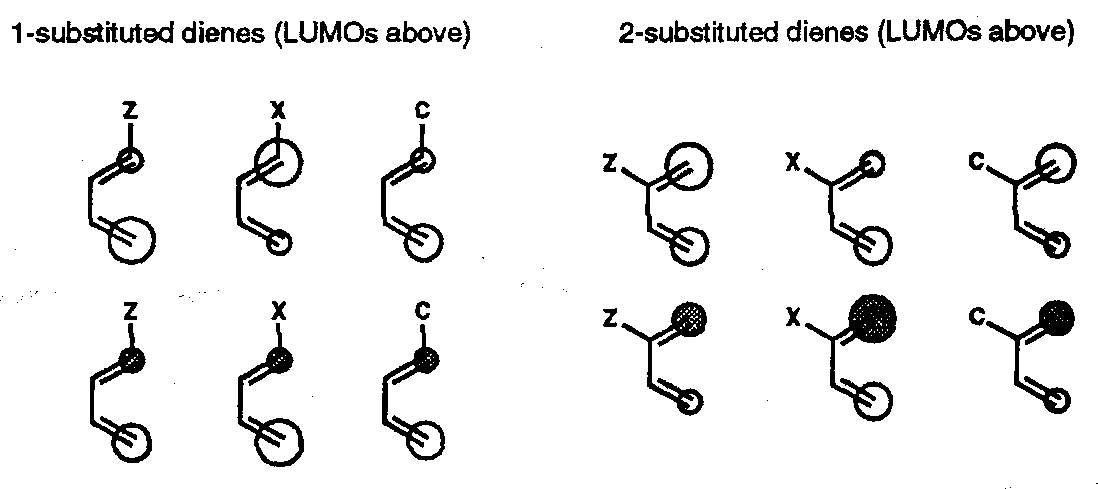
For dienes there are size generic cases (only the coefficients of the terminal positions are shown):

The diene HOMO-dienophile LUMO interaction usually dominates; for 1-substituted dienes the larger HOMO coefficient is at the remote terminal carbon; for 2-substituted dienes the larger HOMO coefficient is at the closer terminal carbon.

Taking the second example above, a 1-Z-substituted diene reacts with a Z-substituted dienophile, i.e.

The same result would be predicted if the diene LUMO and dienophile HOMO had been considered.

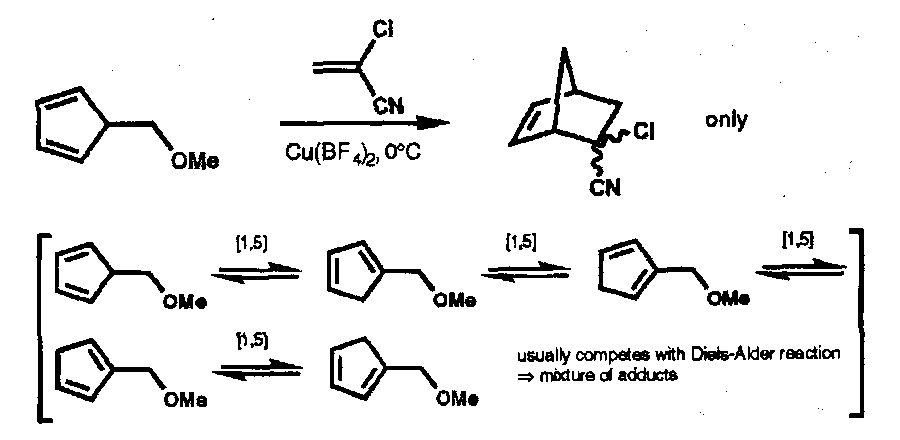
Lewis Acid Catalysis

Diels-Alder reaction are usually accelerated by Lewis Acid catalysis and an increase in the regio- and stereoselectivity is often observed.

Rate Enhancement

Improved Regioselectivity

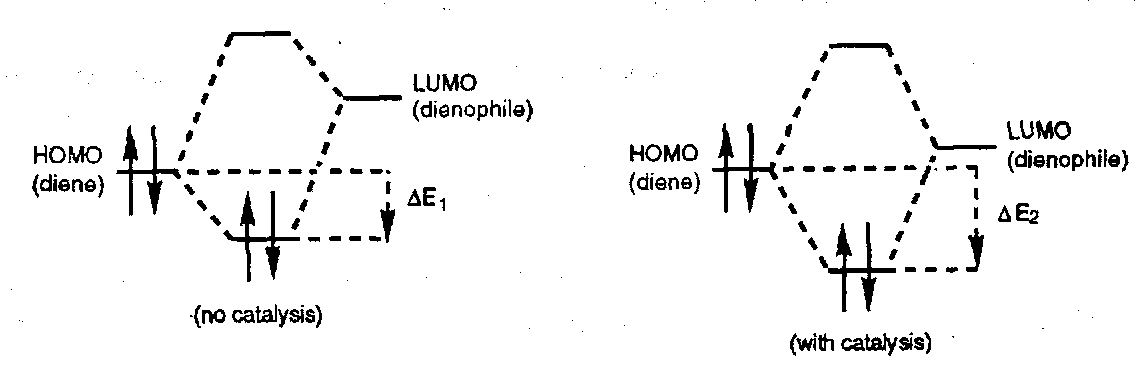
Adding a Lewis Acid results in reversible complexation to Lewis basic sites. Complexation to the dienophile increases the electron withdrawing ability of the activating substituent; the LUMO is lowered and the HOMO(diene)-LUMO(dienophile) gap decreases resulting in a more favourable transition state and a faster reaction.

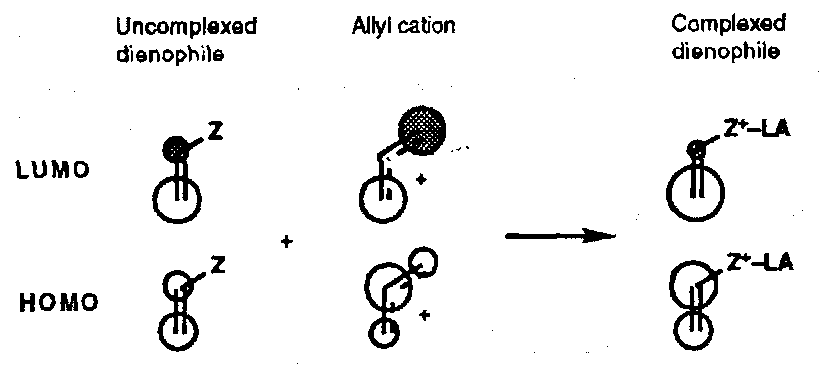
Complexation of the Z substituent on the dienophile imparts some of the orbital characteristics of an allyl cation, and the coefficients are altered accordingly:

There is a larger difference between the orbital coefficients in the LUMO which results in an enhancement of the regioselectivity.

Lewis Acid complexation also enhances the endo- selectivity of Diels-Alder reactions, but arguments involving favourable secondary interactions may not be valid; increasing favourable electrostatic interactions may be of more importance.

[2+2] Cycloadditions

When considering the overlap of the HOMO of ethene and the LUMO of a second molecule of ethene it is clear that a suprafacial-suprafacial interaction is disfavoured (no net bonding):

However, if the two components approach in a crossed-transition state favourable overlap can be achieved:

This approach is suprafacial with respect to the HOMO component and antarafacial with respect to the LUMO component. This [π2s + π2a] cycloaddition is therefore favourable in terms of overlap of the orbitals but is difficult to achieve in practice since the substituents on one alkene have to be oriented directly towards the molecular plane of the second alkene which is sterically unfavourable.

Photochemically induced [2+2] cycloadditions can (but often don’t) proceed through a concerted [π2s + π2s] pathway since under these conditions one of the alkenes will be excited; illustrating with ethene itself:

Unsaturated components that form part of a cumulated π-system (allenes, ketenes, and heteroatom analogues) undergo rapid [2+2] cycloaddition at or below room temperature. In this case of [2+2] cycloadditions of ketenes it is insufficient to consider the ketene molecular orbitals as merely two orthogonal π-systems since orbital mixing with the C-H bonds and oxygen lone pairs is significant: molecular orbital calculations show the FMOs to have the form shown:

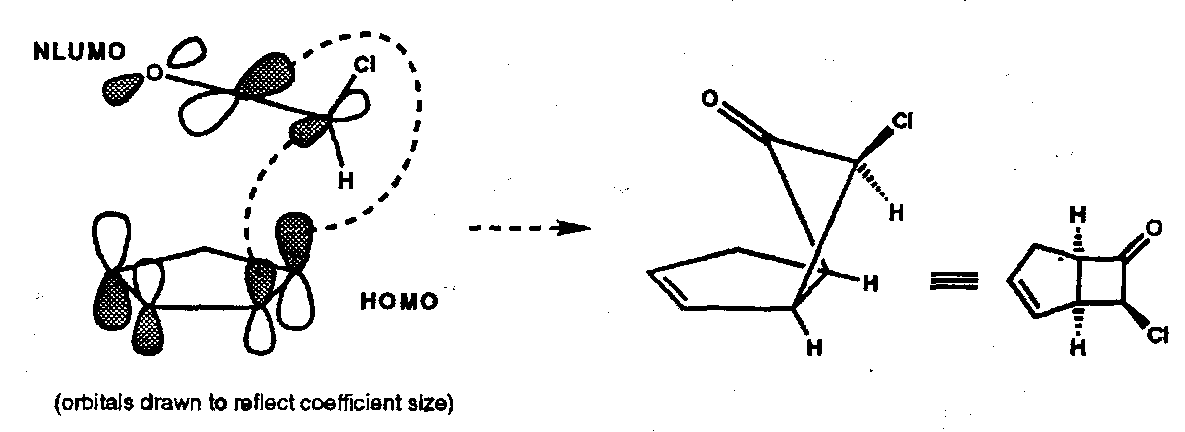
Because the terminal carbon atom in the C=C bond is the site of a node (a zero orbital coefficient) in the LUMO the significant interaction of the second alkene component’s HOMO must be with the next available unoccupied MO (NLUMO) if bonding to that carbon is to be achieved. Thus the orbital picture for the cycloaddition looks like:

This [π2s + π2a] orientation has further consequences:

1. in reactions with an unsymmetrical alkene the less sterically demanding C=O part of the ketene will be oriented above the larger alkene substituents;
2. if an unsymmetrical ketene (R1R2C=C=O) reacts with an alkene the favoured transition state will have the larger of the two substituents oriented away from the plane of the alkene;
3. applying the rule of favoured bonding between atoms bearing larger orbital coefficients allows the regioselectivity of the process to be predicted.

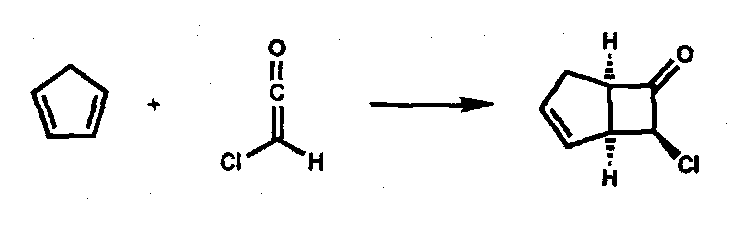
A useful example that illustrates all of these points is the reaction between chloroketene and cyclopentadiene which reacts to give a single [2+2] cycloadduct, the regiochemistry being dictated by the large NLUMO coefficient on the ketene central carbon and a large HOMO coefficient on the terminal carbon of the butadiene substructure in cyclopentadiene.

Via:

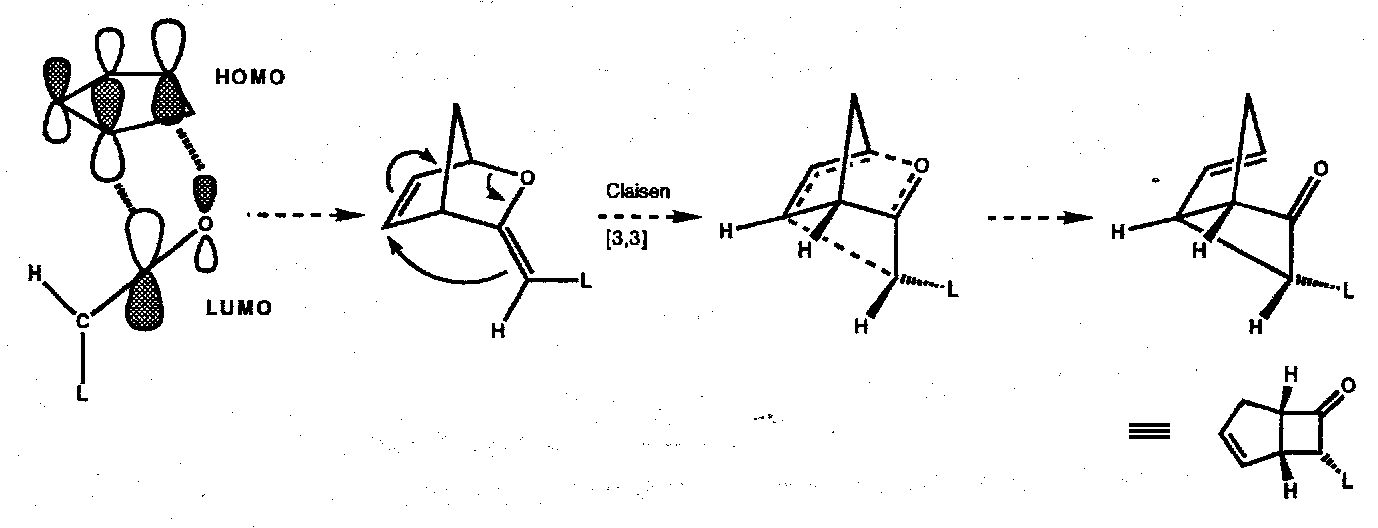
But it not be as “simple” as this. Recent experimental and theoretical work showed that, at least for the case of diphenyl ketene and cyclopentadiene the reaction is not a genuine [2+2] cycloaddition but a stepwise process consisting of Diels-Alder reaction following by a Claisen rearrangement (see below).

In this reaction mode, just the C=O bond of the ketene is involved in the first (regio- and stereochemistry dictating) step, therefore the diene HOMO may usefully interact with the ketene LUMO. The ketene can orient itself with the large group away from the plane of the diene to result in a specific stereochemistry in the adduct. Subsequent Claisen rearrangement (a [3,3] sigmatropic process which is suprafacial in all components) gives rise to the same product that we predict on the basis of a [2+2] cycloaddition:

It is too early to say whether this is the preferred mode in the majority of ketene “[2+2]” cycloadditions.

Vinyl Cations

Related to ketene cycloadditions are the group of cycloadditions with vinyl cation intermediates, e.g. the reaction of allene with hydrogen chloride:

Vinyl cations, like ketenes, have two p-orbitals at right angles to each other, and overlap can develop to each simultaneously, just as with ketenes. In a sense, a ketene is merely a special case of a vinyl cation, with the carbonyl group a highly stabilised  carbocation.

Other [4+2] Cycloadditions

Oxyallyl-diene

Allyl Cation-Diene (similar)

Allyl Anion-Alkene (reverse process)

1,3-Dipolar [3+2] Cycloadditions

The 1,3 dipole reacts with alkene/alkyne to form a hetero-atom containing double/triple bond in a ring. The dipole is isoelectronic with an allyl anion, and so can usually be made up by many combinations of S, N, O and C.

Generally, the mechanism may occur as:

Note that ozone has a 1,3 dipole, and so Ozonolysis is an example of this type of reaction.

Ozone

Azomethine Ylids

TCNE Oxide (a carbonyl ylid, similar)

Chelotropic Reactions

These are cycloadditions and their reverse (extrusion) during which two σ-bonds are made to a single atom. Examples include extrusion of carbon monoxide from oxabicycloheptanes:

Of more importance are singlet carbene additions to alkenes generating Cyclopropanes. Even with dienes Cyclopropanes are formed; the reaction is stereospecific:

A side-on approach can accommodate simultaneous HOMO-LUMO overlap in either combination. This is a [π2s + ω2a] process:

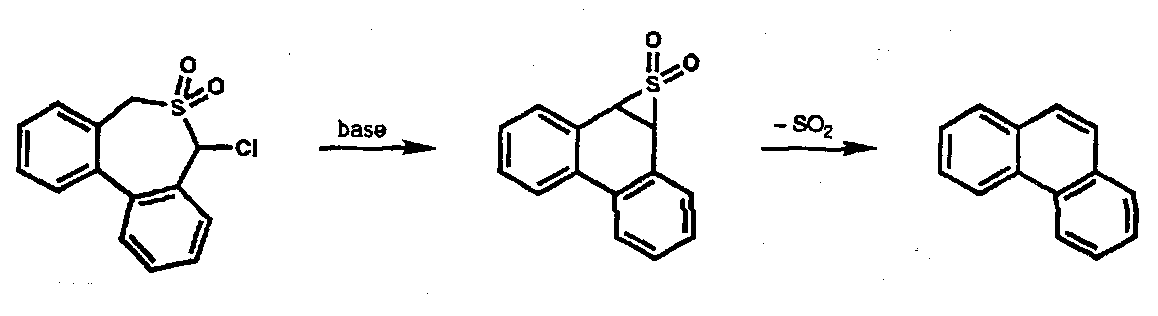
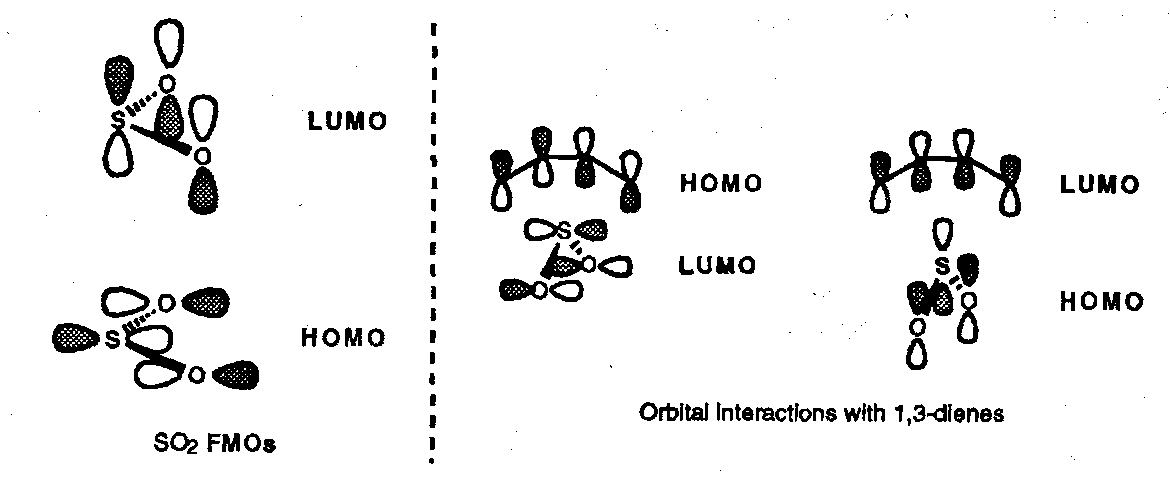
Both of these processes are essentially irreversible; reversible Chelotropic reactions are seen in the chemistry of sulphur dioxide; in this case orientation of SO2 is head-on (in contrast to carbenes). Extrusion of SO2 occurs from episulphones during the Ramberg-Backlund alkene synthesis.

Reaction with 1,3-dienes is reversible; the sulphones are useful precursors for controlled formation of dienes.

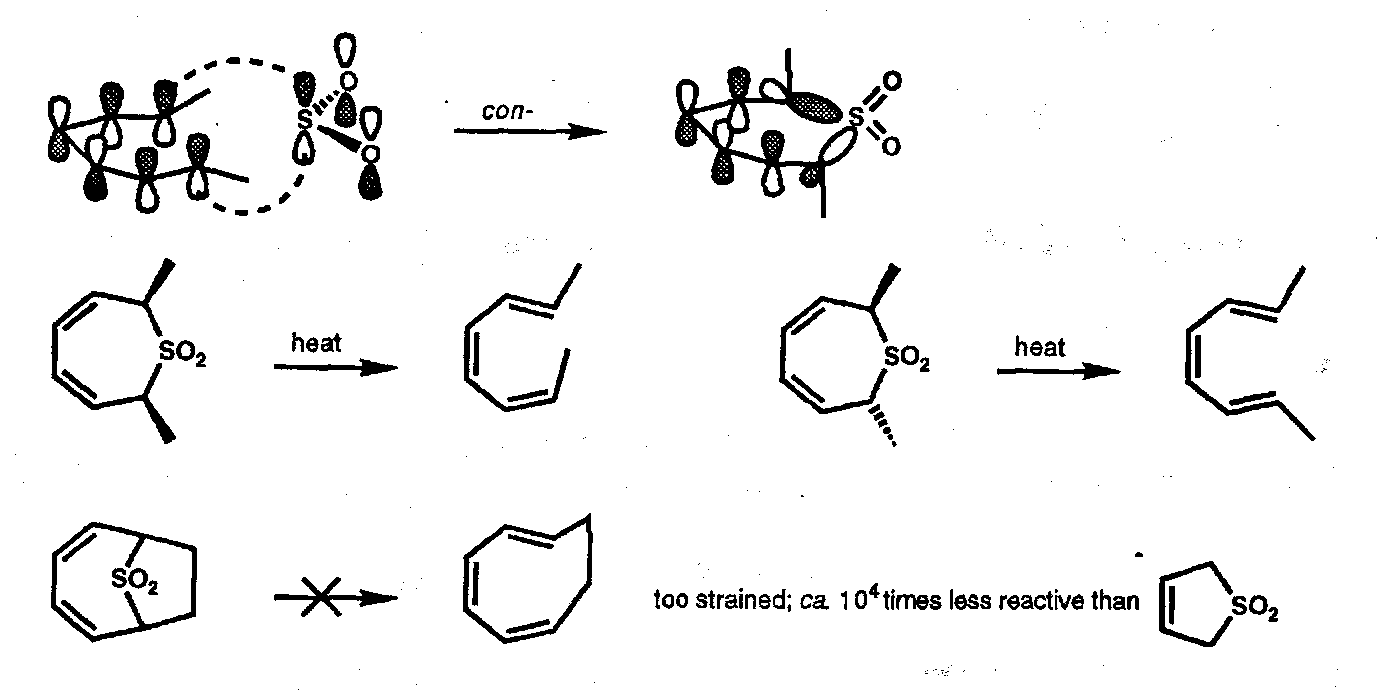
This is suprafacial with respect to both diene and sulphur atom, [π4s + ω2s]. The extrusion process is disrotatory.

With trienes the extrusion process dominates but considering the reverse process the reaction must be antarafacial with respect to the alkene π-system and suprafacial with respect to the sulphur atom, [π6a + ω2s]. This results in conrotatory ring opening during the extrusion with the result that certain bicyclic sulphones undergo SO2 extrusion extremely slowly (probably via diradical mechanism):

Electrocyclic Reactions

These are pericyclic processes in which a ring is formed or opened in an intramolecular way. Woodward & Hoffmann provided an early (workable) means for predicting the stereochemistry of these processes (a simplification of the correlation diagram approach discussed earlier).

This modifies the Woodward-Hoffmann Rules slightly, since this con/dis consideration must be added. Basically, all thermal reactions involving 4n+2 electrons are allowed if disrotatory, and all thermal reactions involved 4n are allowed if conrotatory. Photochemical reactions are then the opposite.

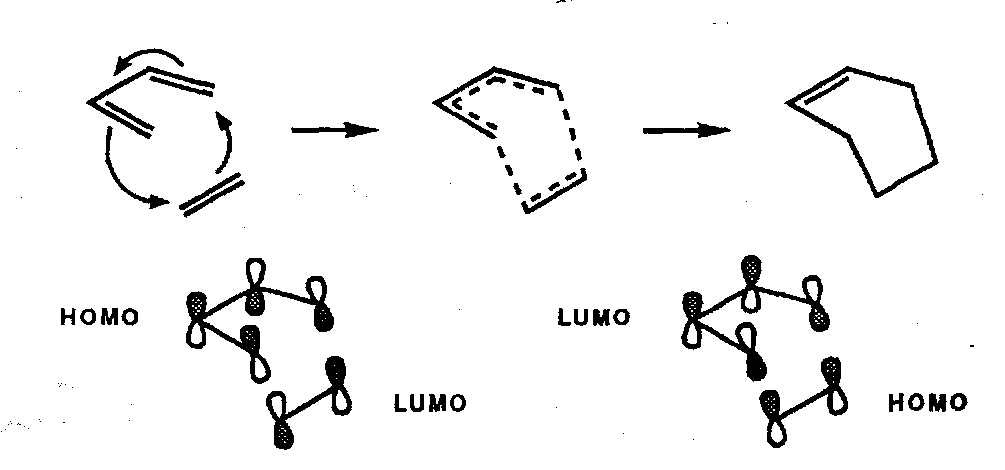
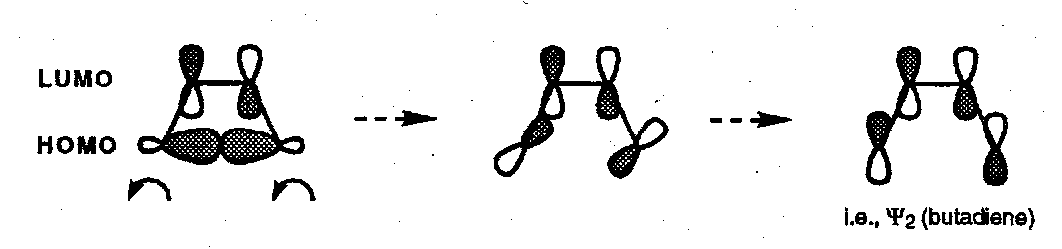
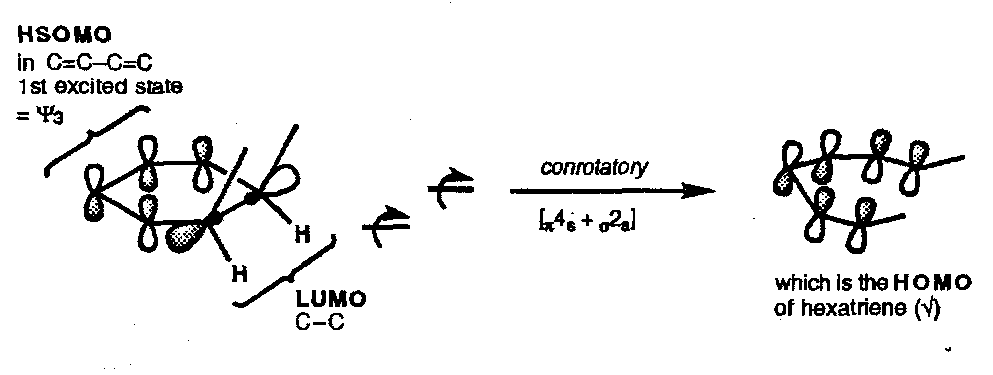
In this analysis the mode of rotation is determined by the phase properties of the HOMO (in the ring closure process). Thus, although cyclobutene opens thermally to butadiene, its mode of ring opening is inferred by analysing the reverse process.

The HOMO for the thermal case is ψ2 (one-node); that for the photochemical case is ψ3 (two nodes) giving the complementary stereochemical outcome.

This approach is essentially a truncated version of the FMO method which may be easily applied to both the forward and reverse reactions:

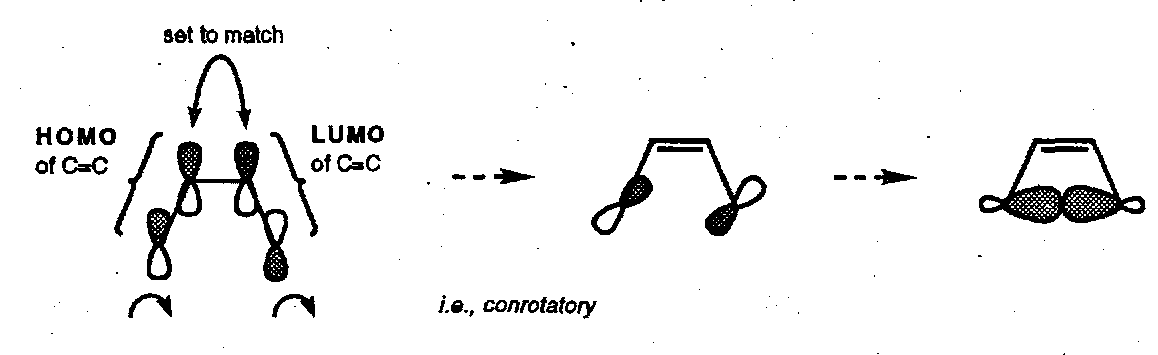
Cyclobutene Ring Opening

Note that this process may equally well be designated as [π2a + σ2s] or as [π2s + σ2a] depending on how the matching lobes are chosen.

Butadiene Ring Closure

Have to designate one alkene to be the HOMO component and one as the LUMO component (entirely arbitrarily). Since a new double bond is being made the phases at this position must be set to match for this to work. [π2s + π2a]:

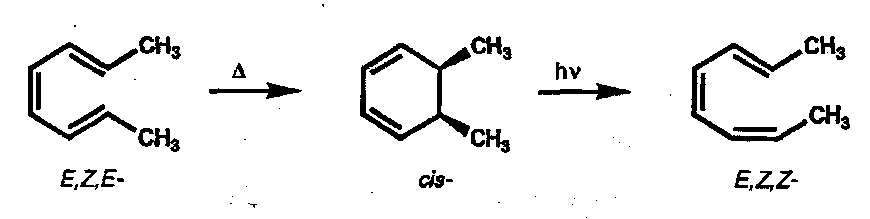
Hexatriene Ring Closure (and the reverse)

Ring closure is the preferred mode for the thermal reaction. The FMO approach is similar to that used above:

Thermal Ring Closure

Photochemical Ring Closure

FMO theory is a little clumsy in these electrocyclic reactions and it may be found easier to use the Woodward & Hoffmann “HOMO” method.

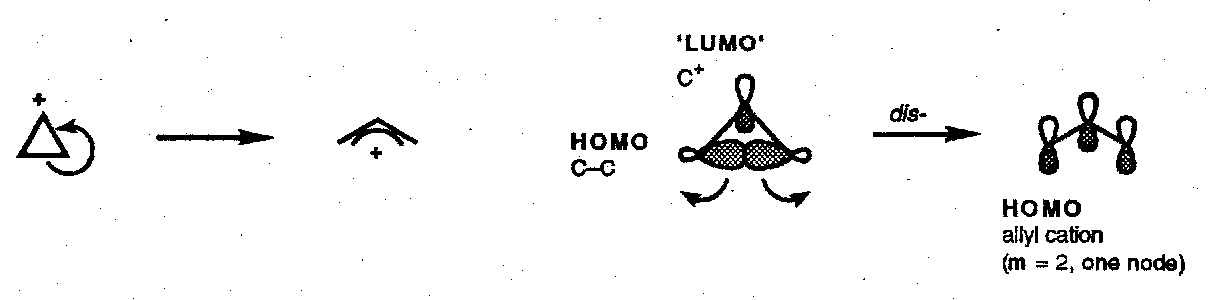
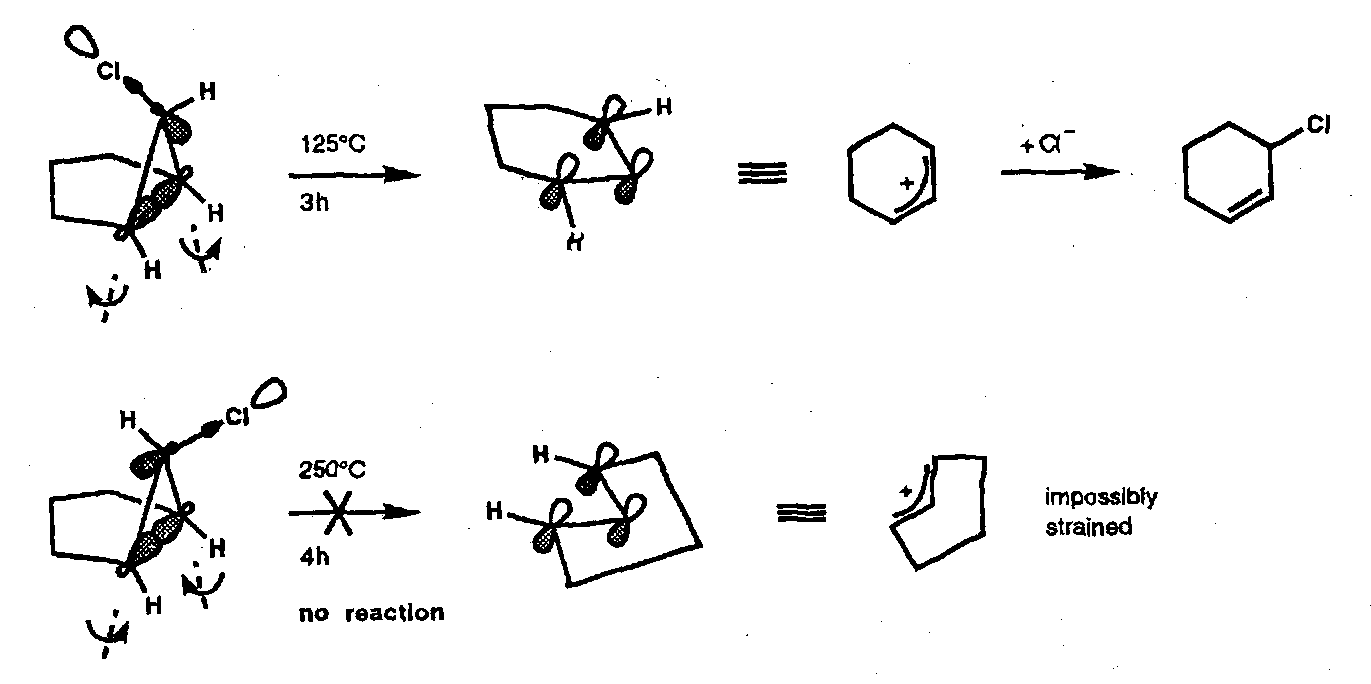
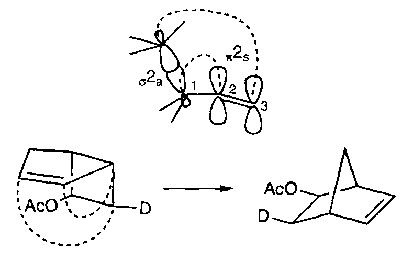
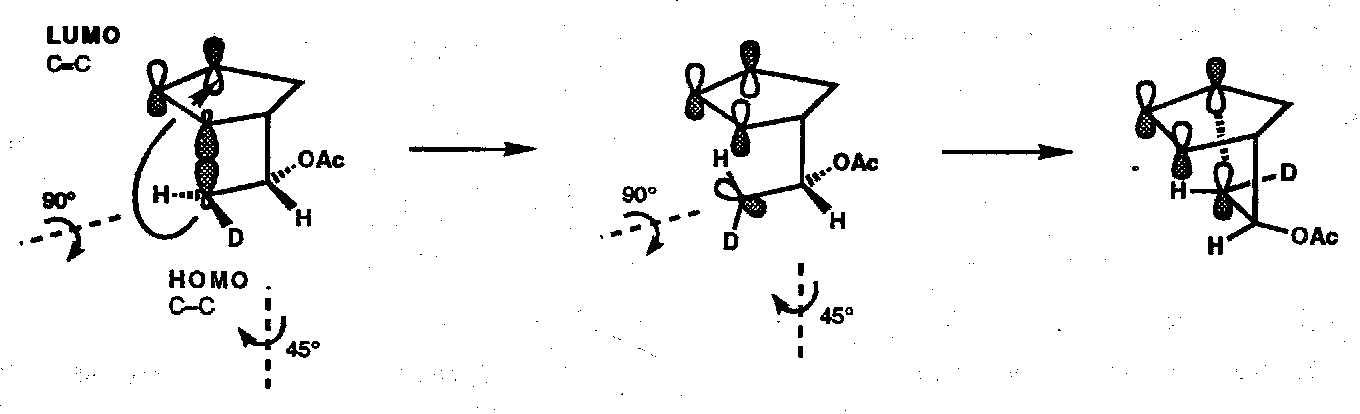
Cyclopropyl Halide Solvolyses

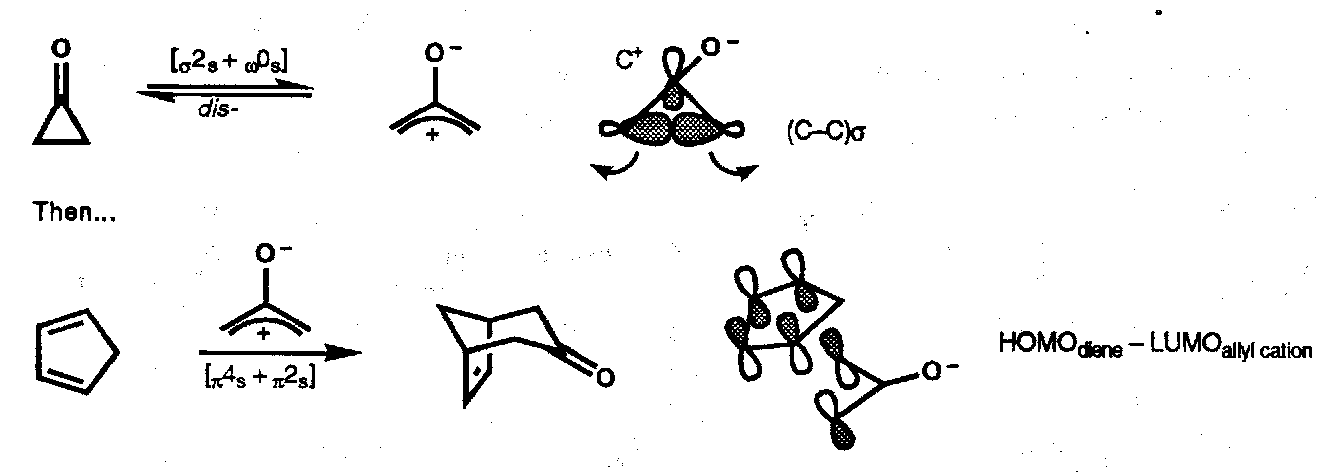
The cyclopropyl cation to allyl cation conversion is a [σ2s + ω0s] electrocyclic process that proceeds with disrotatory opening.

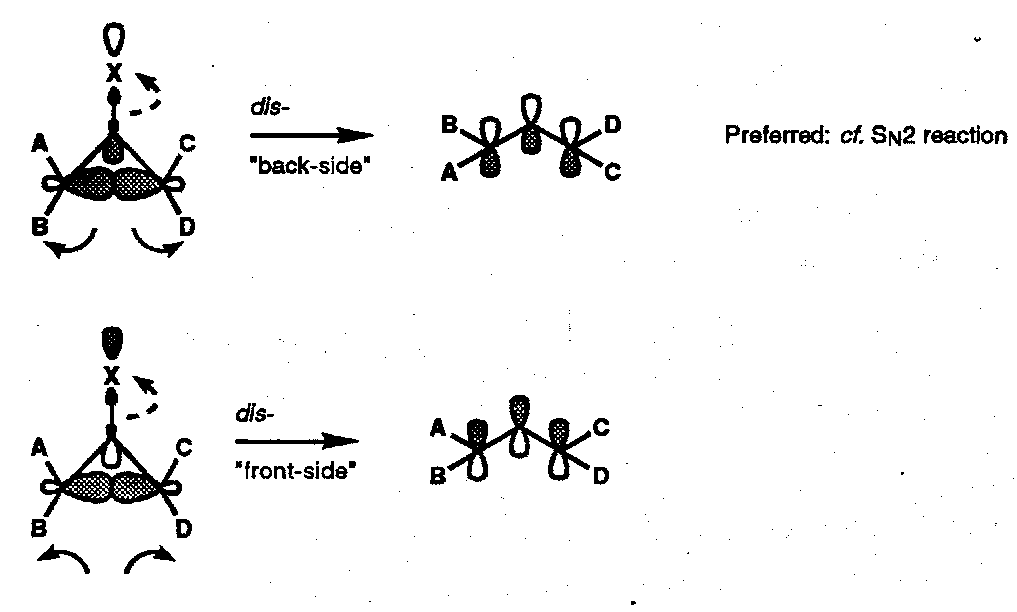
The ionisation of cyclopropyl halides and tosylates is a concerted process (i.e. that does not proceed through a discrete cyclopropyl cation) and can be viewed as an internal elimination in which the σ-bond electrons (HOMO) feed into the (empty) σ*-orbital (LUMO) of the C-X bond. Thus, not only is the ionisation disrotatory, but the sense of rotation is specified; this has important consequences for the reaction rate:

Endo- substituents A, C are brought together in the transition state, whereas exo- substituents B, D are moved apart. This is reflected in the relative acetolysis rates shown; whilst more phenyl substituents allow additional mesomeric stabilisation of the allyl cation. Their effect is greatest when they are sited exo- with respect to the leaving group.

A further consequence of this sense of disrotatory opening is that diastereomeric fused bicyclic cyclopropyl halides behave dramatically differently when heated; only leaving groups in the endo- position are capable of being ejected in a concerted manner.

Sigmatropic Rearrangements

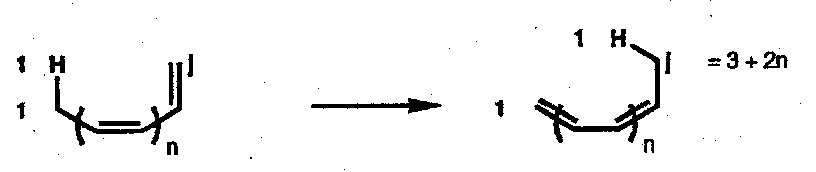
A sigmatropic change of order [i,j] was defined by Woodward & Hoffmann as the migration of a σ-bond, flanked by one or more π-electron systems, to a new position whose termini are i-1 and j-1 removed from the original bonded atoms, in an uncatalysed intramolecular process.

Illustrated for [1,j] hydrogen shift:

• number the breaking σ-bond as 1, and count out to the position at which the new bond is made. This number gives the order of the change. In the more general case:

[1,j]-Hydrogen shifts must be suprafacial with respect to the hydrogen atom, but whether a shift is suprafacial or antarafacial with respect to the polyene component will be determined by orbital symmetry.

With groups other than hydrogen, a p-orbital is involved in the shift and suprafacial and antarafacial descriptors need to be applied to the migrating bond as well as the polyene component:

Two equivalent methods are used to predict which operates for a particular shift, either the FMO (HOMO-LUMO) approach or Dewar’s NBMO approach.

Consider a thermal [1,3] hydrogen shift; is it predicted to be suprafacial or antarafacial?

FMO Method

Dewar’s Method

In this treatment the molecule is mentally split, at the σ-bond that breaks, into two radicals; the SOMO for each component is drawn and the symmetry requirements deduced. This predictive formalism implies nothing about the mechanism.

This method also predicts an antarafacial [1,3] hydrogen shift, a [π2a + σ2s] process. However, in practice it is almost impossible for bonding to be maintained in an antarafacial [1,3] H-atom shift and the reaction is not seen thermally. This is an example of a symmetry allowed but geometrically unfeasible reaction.

Photochemical [1,3] H-atom shifts are common because these are [π2s + σ2s] processes.

Thermal [1,5] hydrogen shifts are common; the example is a demonstration of the suprafacial nature of the change. [π4s + σ2s]:

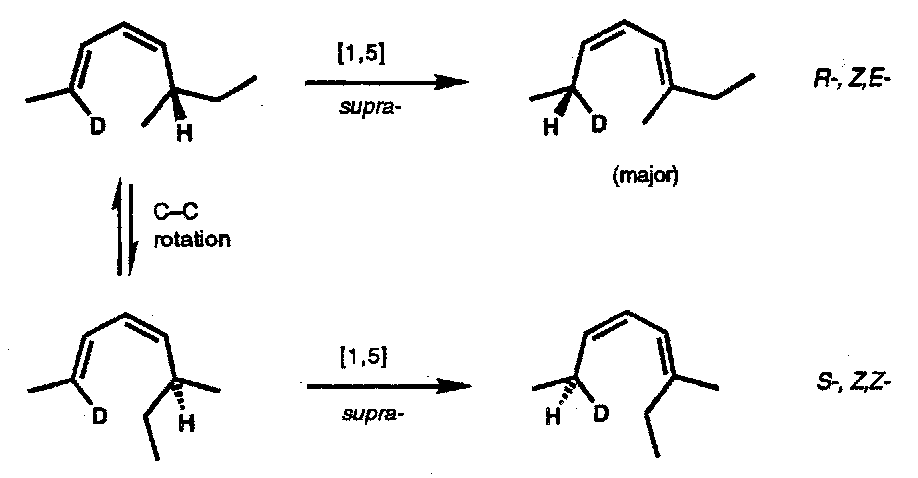
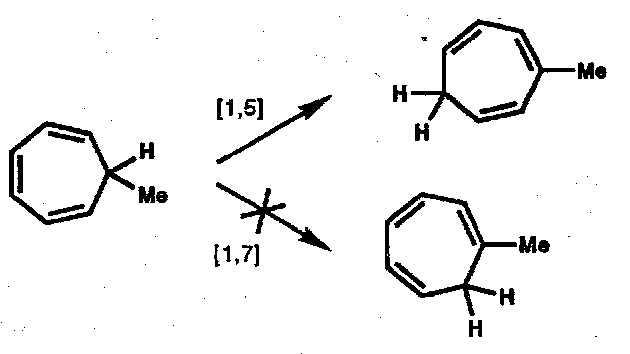
Thermal [1,5] H-atom shifts are particularly fast when the termini are close together as in monosubstituted cyclopentadiene derivatives; here isomerisation is rapid even at 0oC.

Thermal [1,7] H-atom shifts are predicted to be antarafacial [π6a + σ2s] processes; with acyclic trienes there is enough flexibility in the linking chain to allow the antarafacial transfer to proceed through the required helical transition state:

Where a helical transition state cannot be achieved, suprafacial [1,5] H-atom transfer occurs instead:

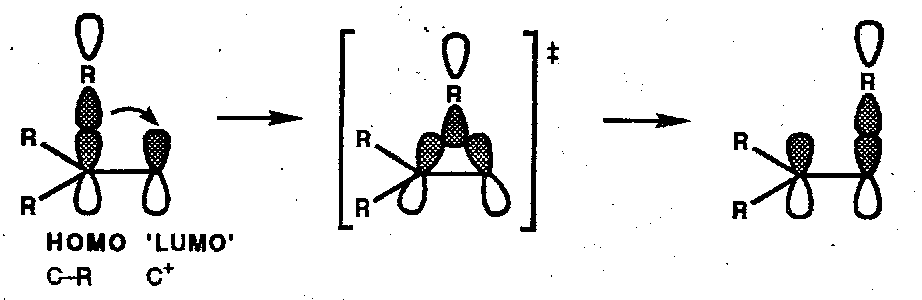
Thermal [1,2] shifts of alkyl groups are also pericyclic processes; one component is a σ-bond, the other an empty p-orbital, i.e. [σ2s + ω0s]:

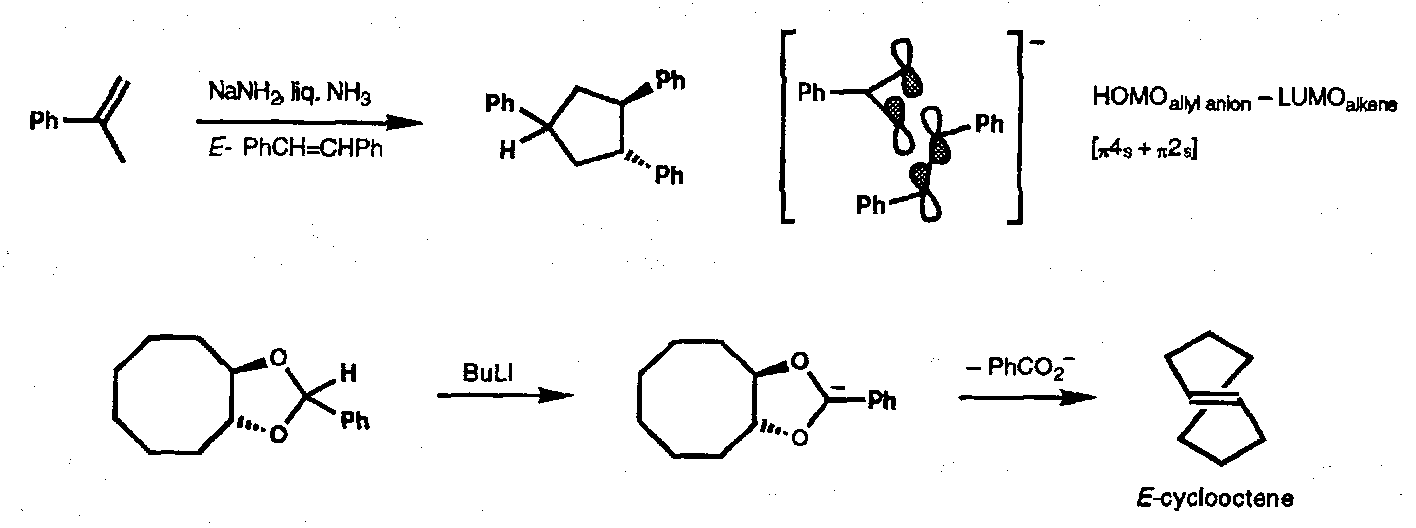
Thermal [1,3] alkyl shifts occur suprafacially with respect to the alkene component which requires inversion at the migrating group (antarafacial). Classic demonstration of this:

The Dewar method can be easily applied to explain this result, but here the FMO method is illustrated:

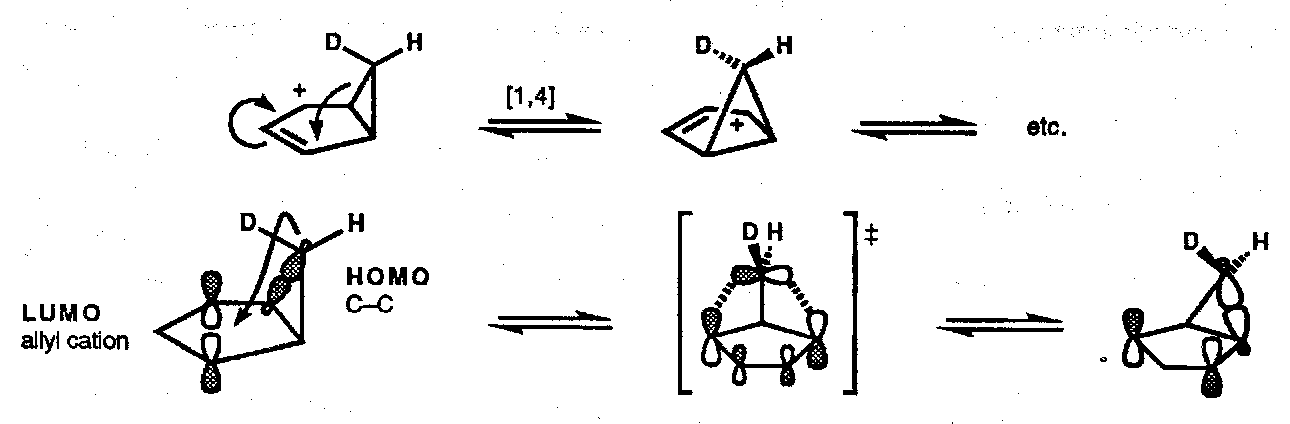
Other alkyl shifts abound; an interesting case is the degenerate thermal [1,4] alkyl shift within bicyclic cyclopropyl allyl cations: [π2s + σ2a]

Thermal [2,3] shifts are common in heteroatom chemistry:

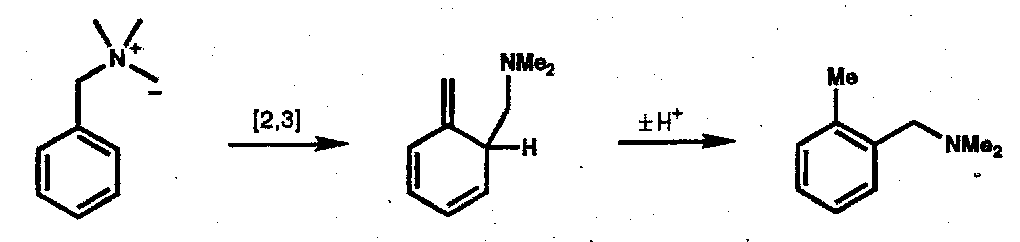
Wittig Rearrangement

Sommelet-Hauser Rearrangement

An analogous reaction of allylic sulphonium ylids yields homoallyl alkyl sulphides.

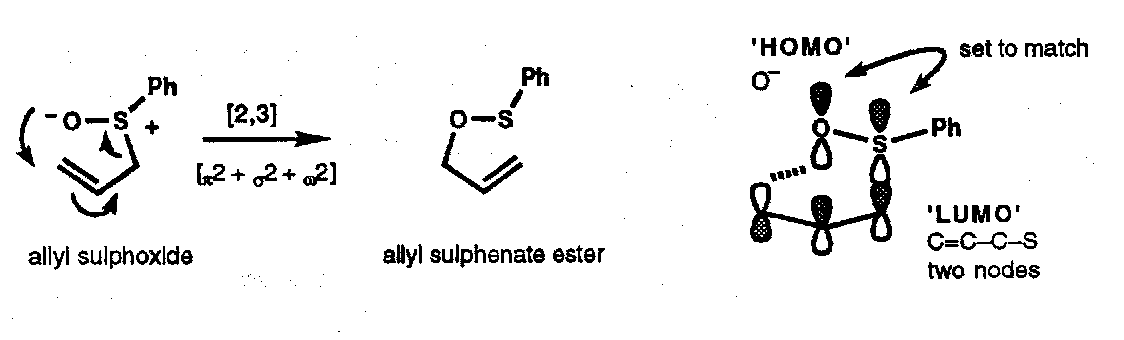
Meisenheimer Rearrangement

Exactly analogous reactions occur with allyl sulphoxides (to give allyl sulphenates), and allyl phosphine oxides (to give allyl phosphinates).

These are difficult to treat since they are formally three component systems; thus the rearrangement of allyl sulphoxides is a [π2 + σ2 + ω2] process.  To treat this in a reasonable way using the FMO approach, we have to mentally combine two of the components to make a new four-electron component, the HOMO of which will contain one node and the LUMO two nodes. Thus, a rationalisation in FMO terms is shown:

Although this seems rather arbitrary, it allows us to use the nodal properties of the orbitals to predict that the new bond to oxygen occurs suprafacially with respect to the allyl component. In fact, all of these thermal [2,3] shifts are suprafacial in all components, [π2s + σ2s + ω2s].

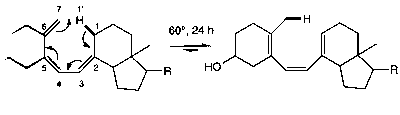
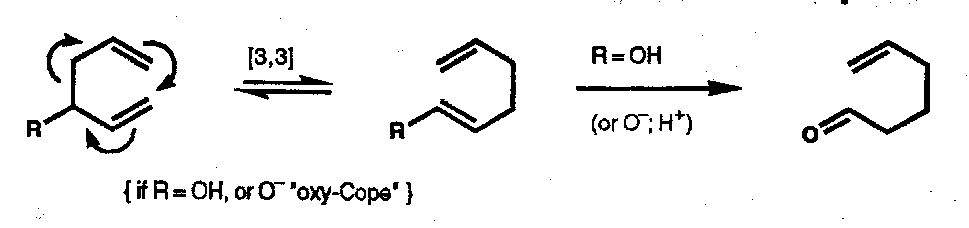
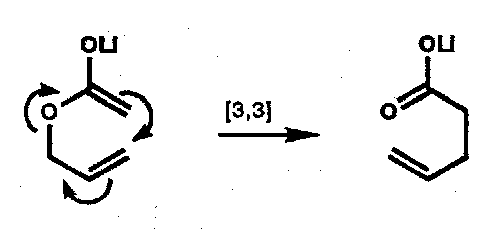
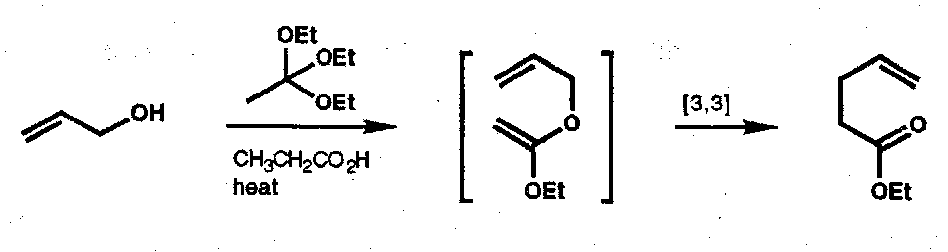
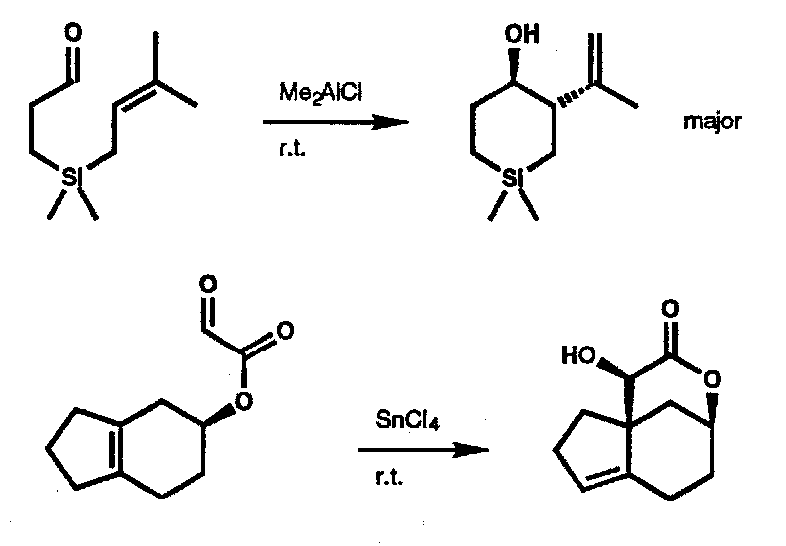
Thermal [3,3] sigmatropic rearrangements form a large class of reactions including famous named examples:

Cope

1,5-diene.

                

Claisen

Allyl vinyl ether.

Ireland-Claisen

Allyl ester enolate.

Johnson Orthoester-Claisen

Allyl alcohol + orthoester.

Eschenmoser-Claisen

Allyl alcohol + orthoamide.

Carroll Rearrangement

Enol of an allyl β-ketocarboxylate.

Often such sigmatropic processes form a key step within a more complex sequence, e.g.

The Dewar procedure can be used to show that these [3,3] sigmatropic rearrangements are suprafacial in all components, i.e. [π2s + π2s + σ2s].

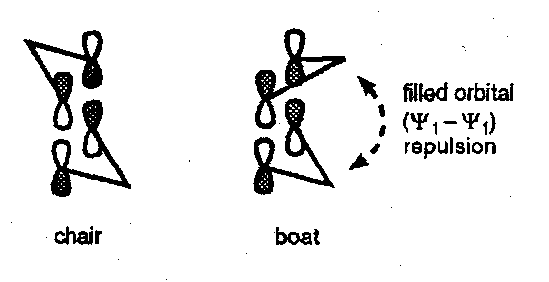
Since ψ1 of an allyl radical is filled, a chair-like transition state is preferred to avoid destabilising non-bonded interactions between the central atoms …

In the FMO treatment of thermal [3,3] shifts we can go a step further and note that there is antibonding interaction in the boat-like conformation not present in the chair-like conformation. Once more, because this is a three-component reaction, we need to take σ2-π2 combination to generate a HOMO with four electrons and view its interaction with a two π-electron LUMO:

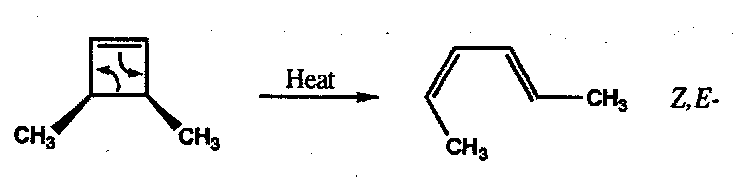
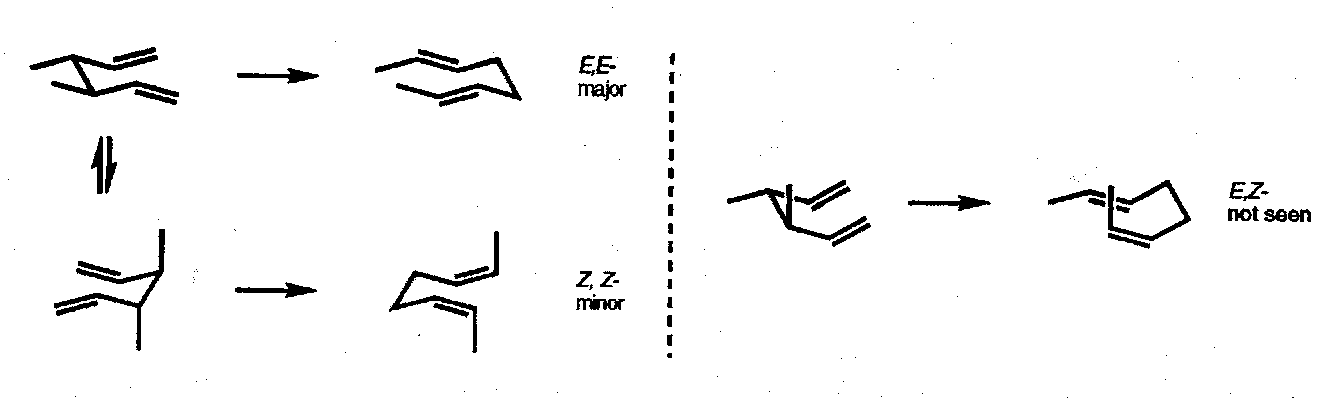
This preference for a chair conformation is strongly followed unless there are steric constraints that impose a boat-like transition state. The requirement for substituents to adopt equatorial sites is a secondary preference as shown by the Cope rearrangement of anti-dimethyl penta-1,5-diene which gives none of the E,Z product that would arise through a boat transition state:

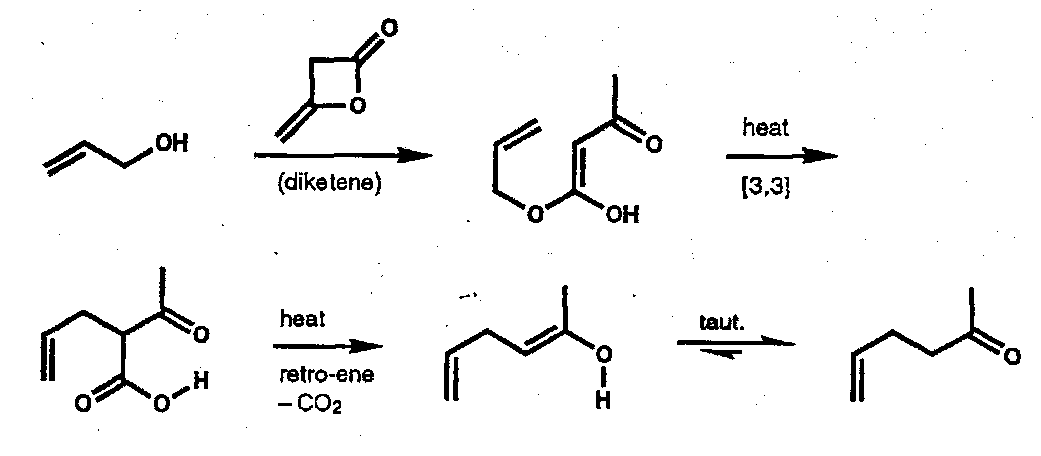
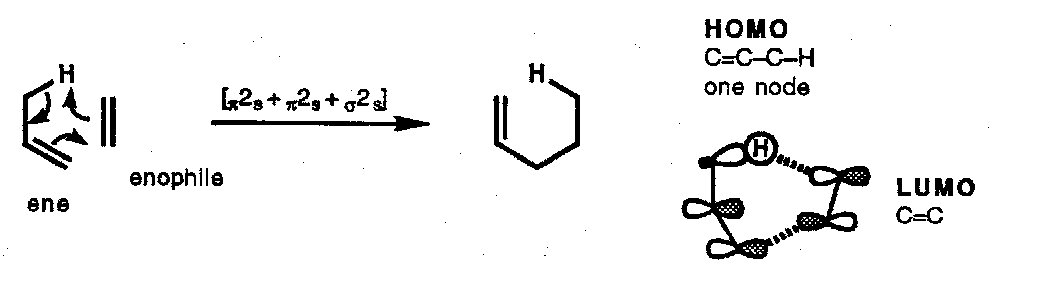
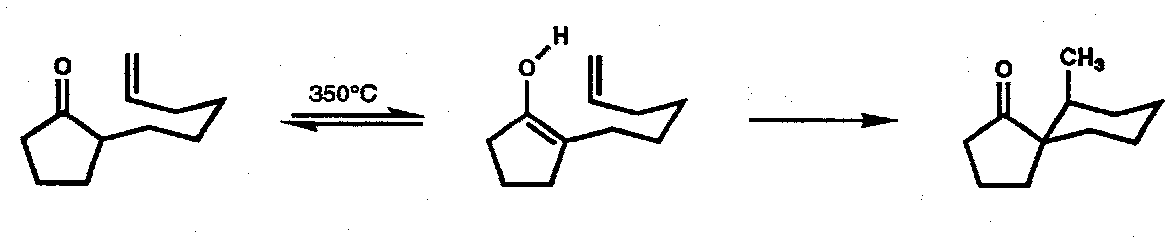
Ene Reaction

Although not a sigmatropic reaction, the ene reaction is mechanistically related to a [1,5] H-atom shift except the two alkene components are not connected with a σ-bond (and are therefore not conjugated). As for the [3,3] shift, the FMO treatment takes σ2-π2 combination (the ene component) and views the interaction with the second alkene (the enophile).

Reactions with SeO2 are often ene reactions as well, such as:

Note that this is then followed by a [2,3] shift.

Ab initio calculations for the simplest case (propene + ethene) suggest a flattened chair or envelope conformation for the transition state.

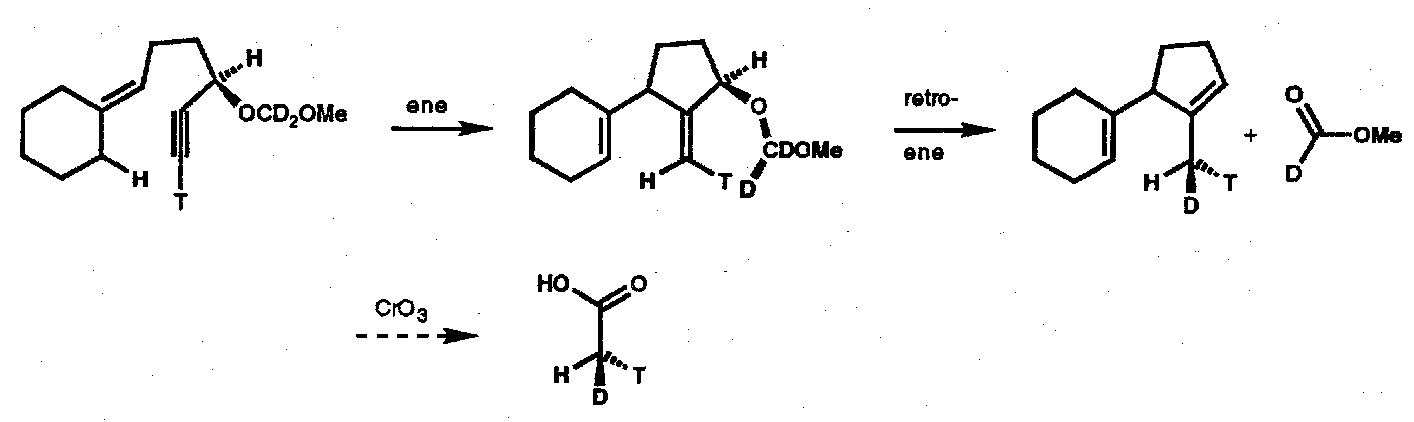
Many examples of both inter- and intramolecular ene reactions are known, e.g.

Synthesis of Chiral Acetic Acid

Carbonyl Ene

(responds well to Lewis Acid catalysis to lower the enophile LUMO energy).

Conia Ene Reaction

(of enol tautomers of unsaturated carbonyl compounds).