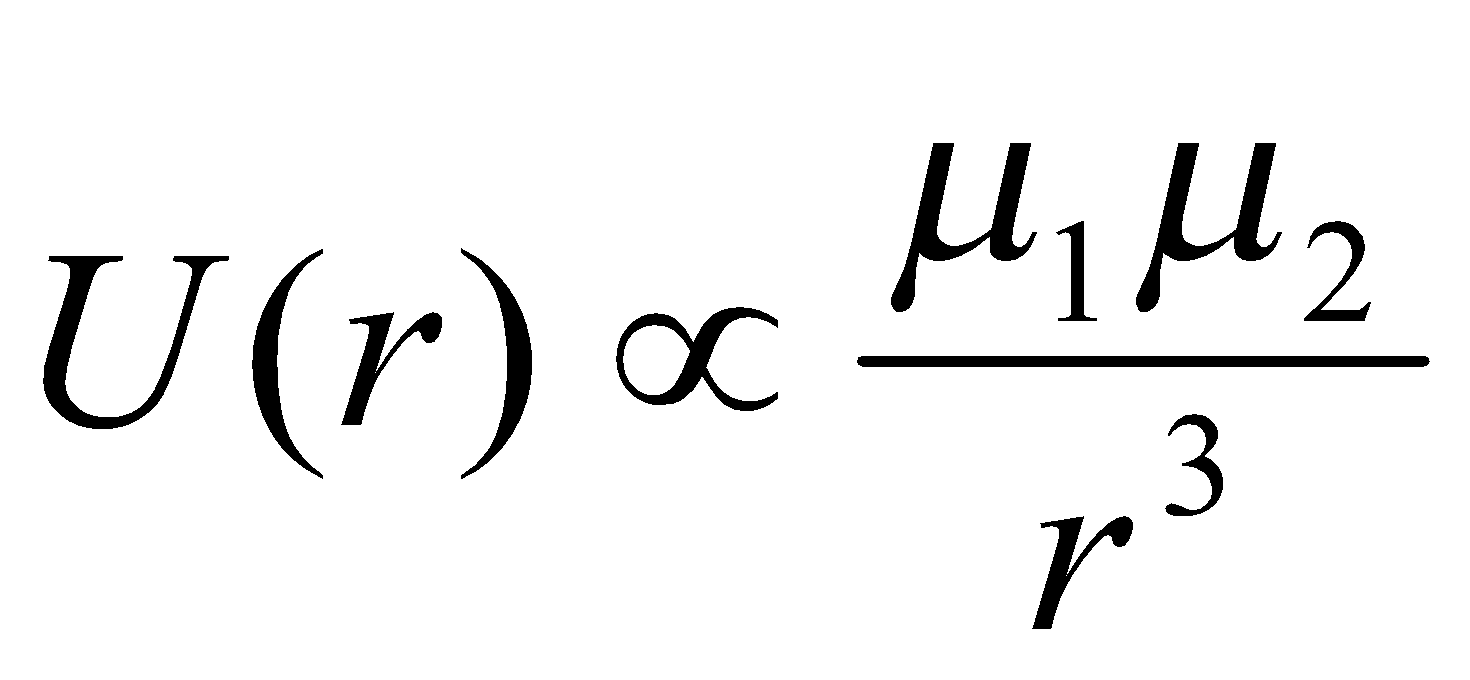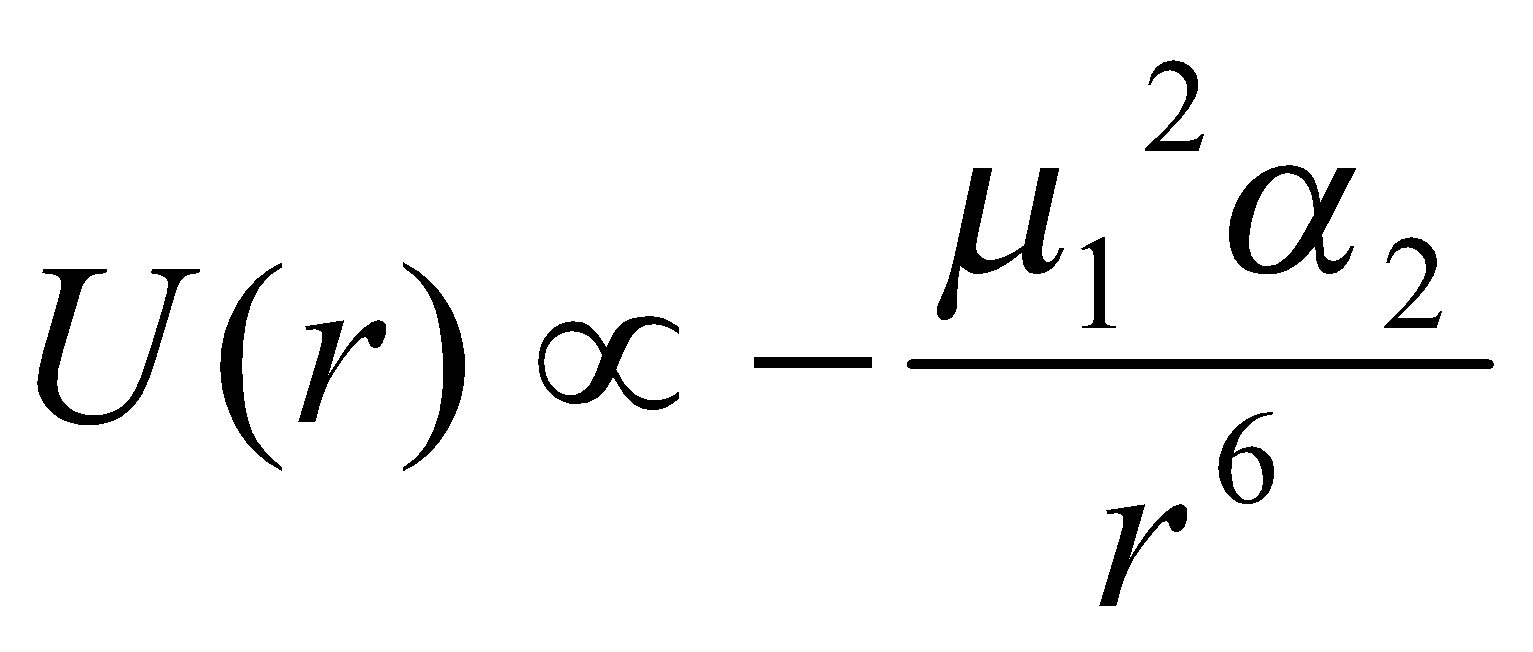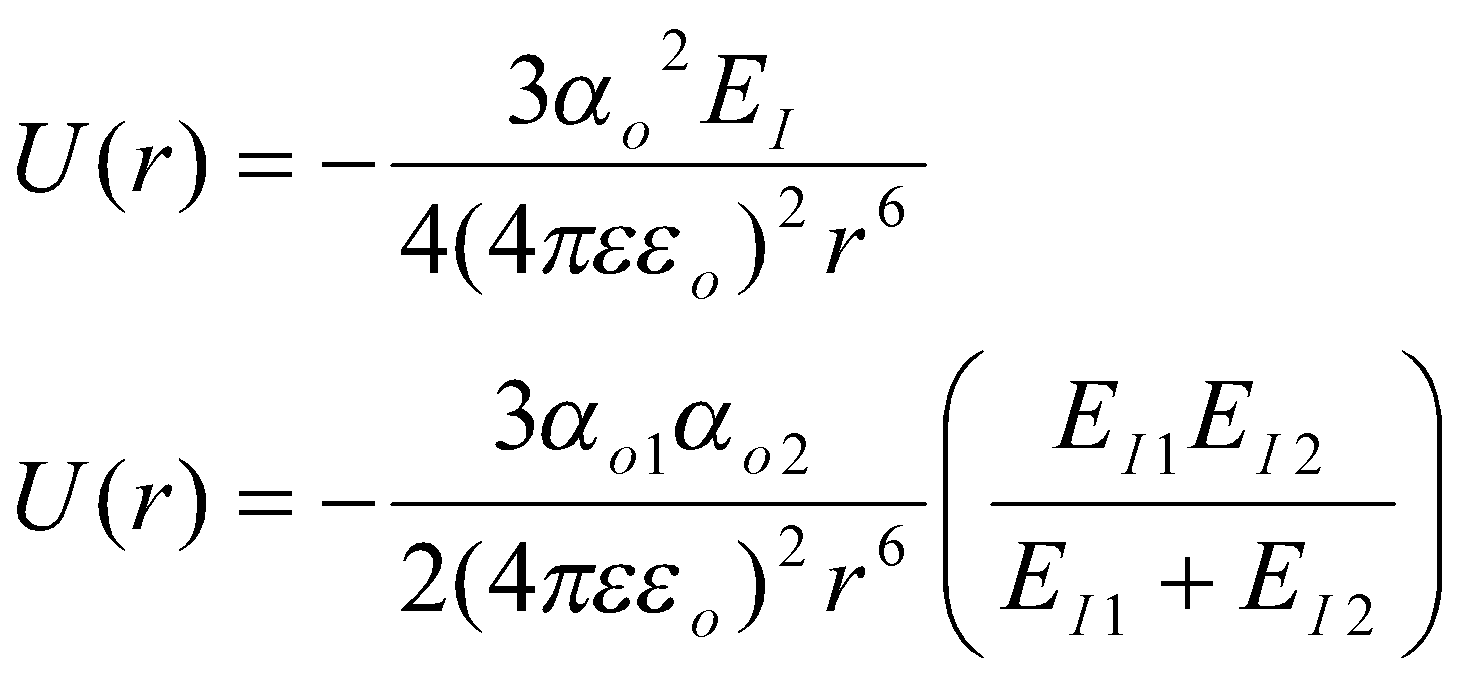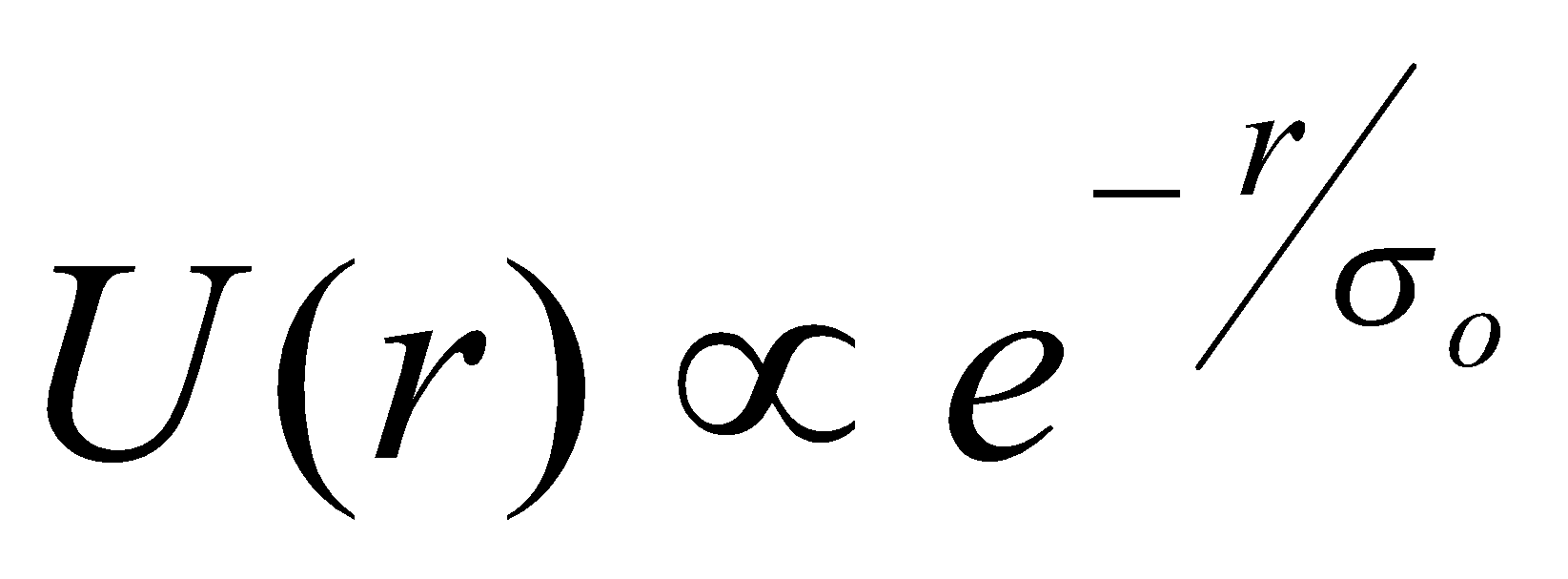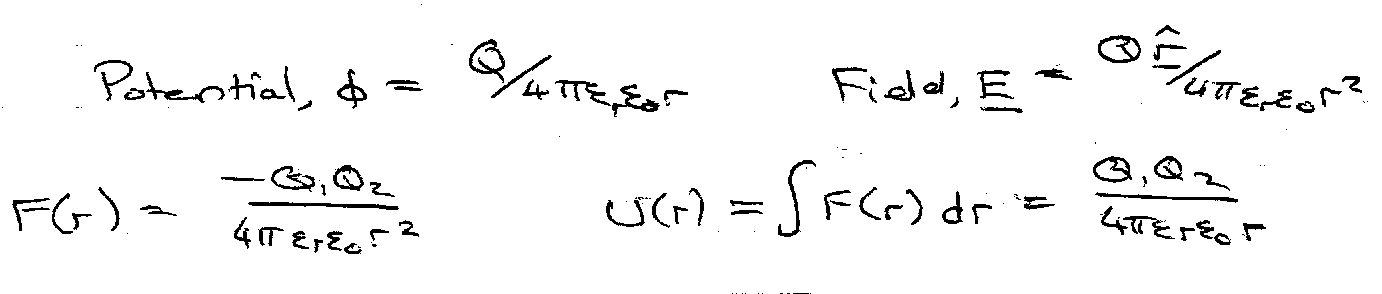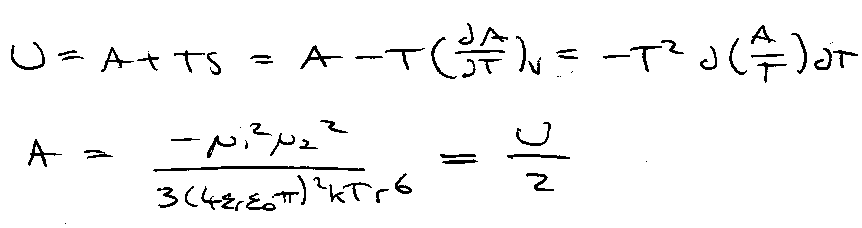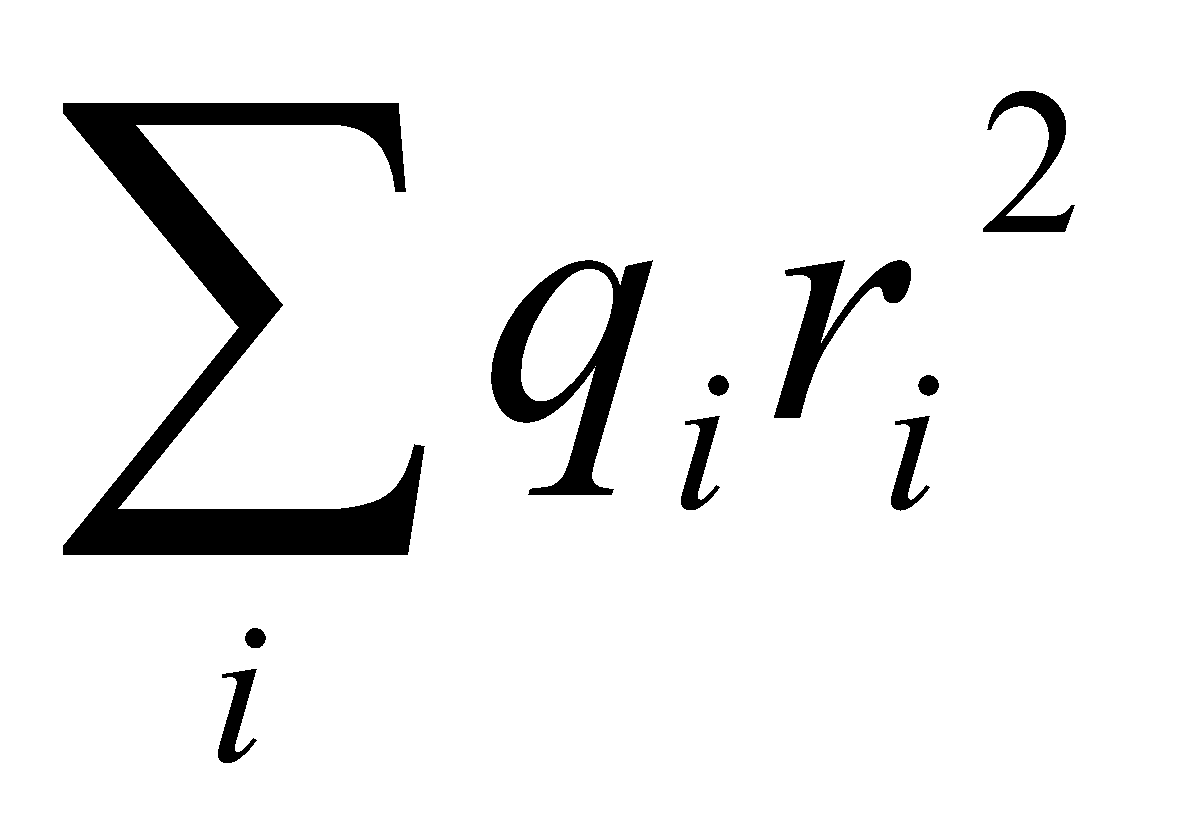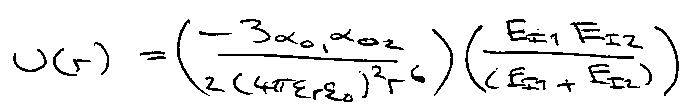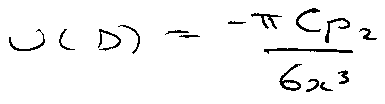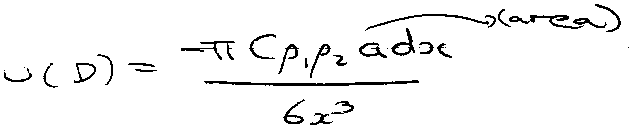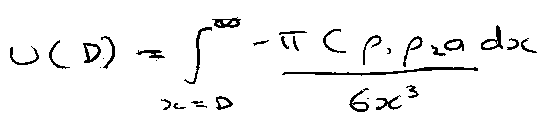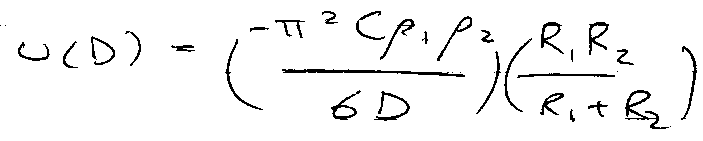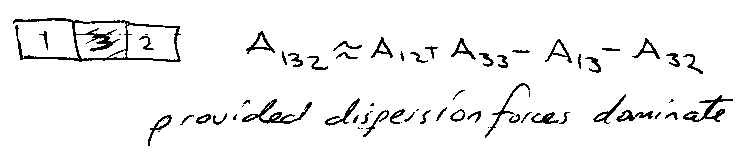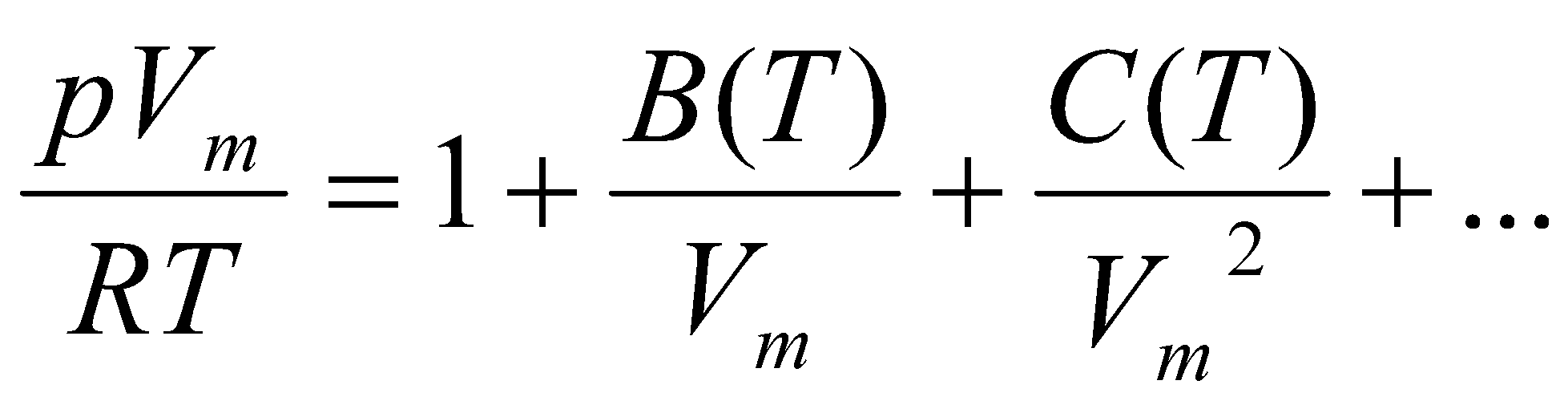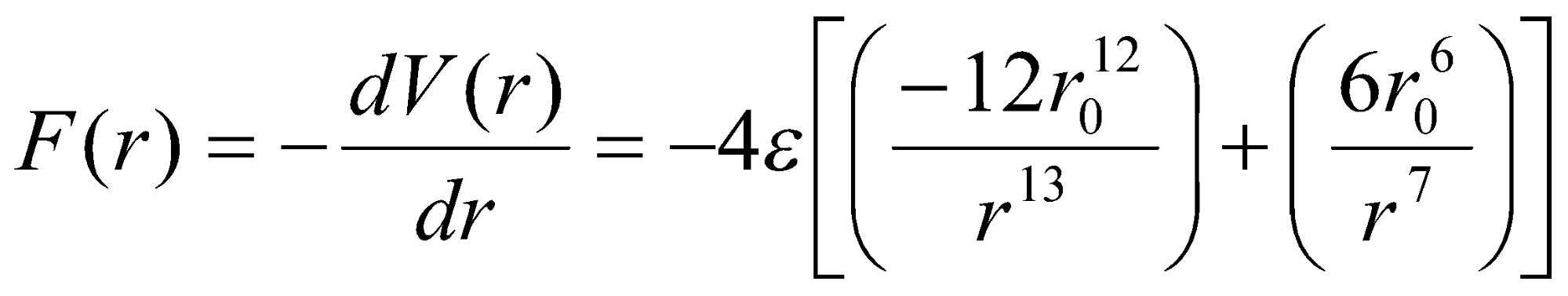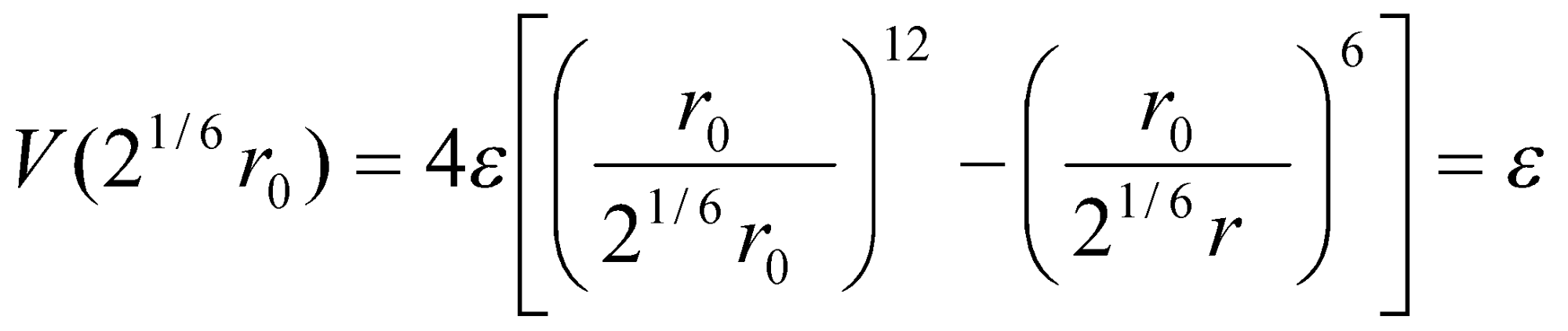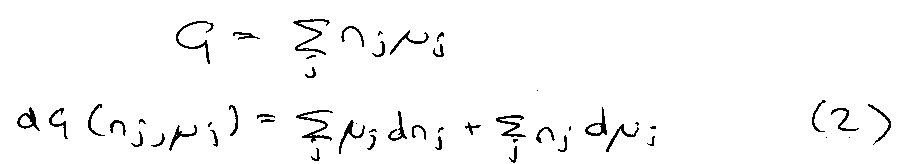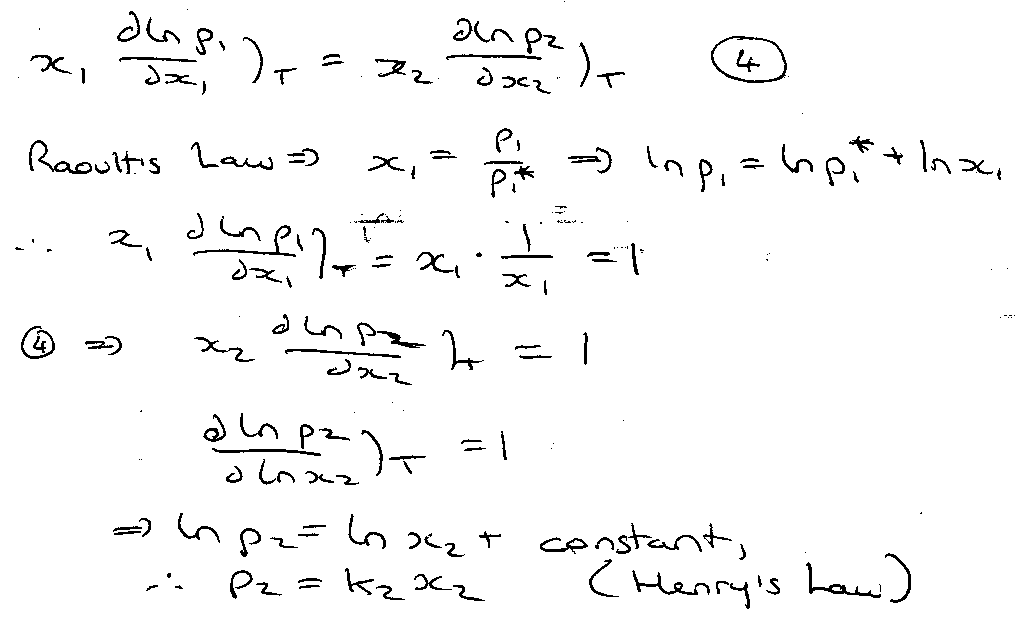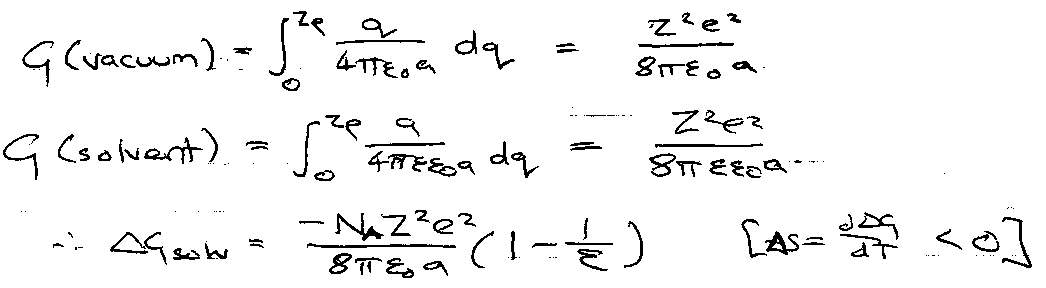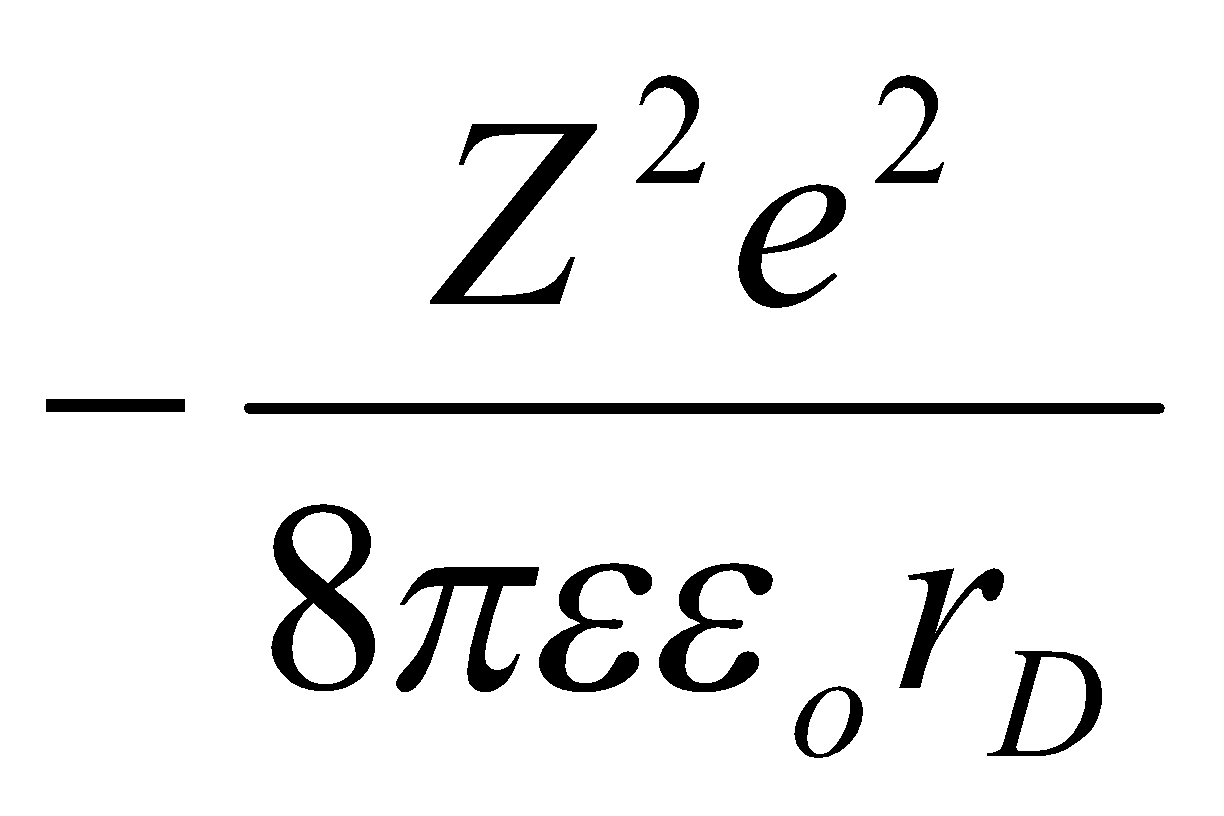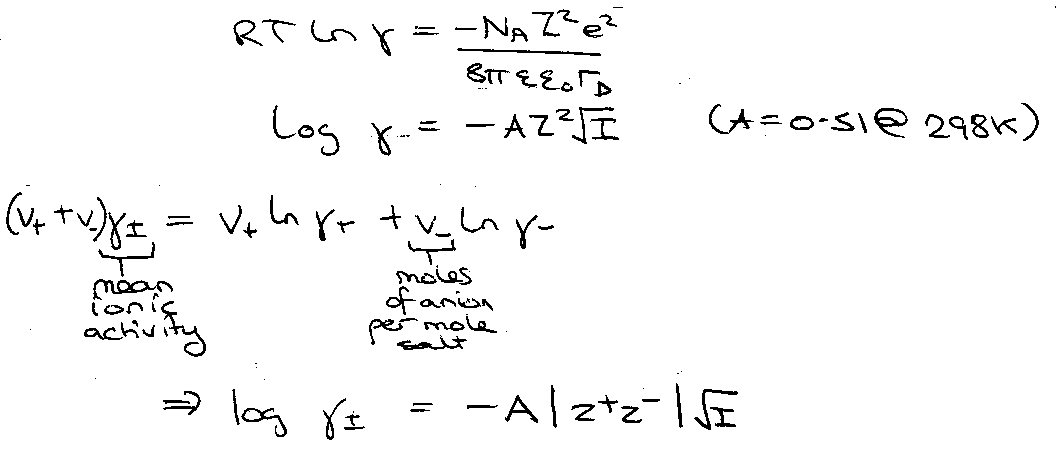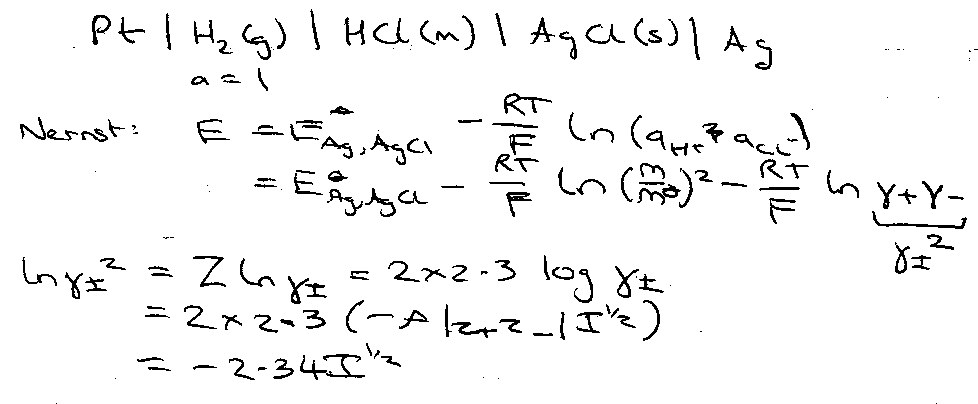Molecular Interactions Notes

Summary of Fundamental Molecular Interactions

Ion-Ion
Ion-Dipole
Dipole-Dipole (fixed)
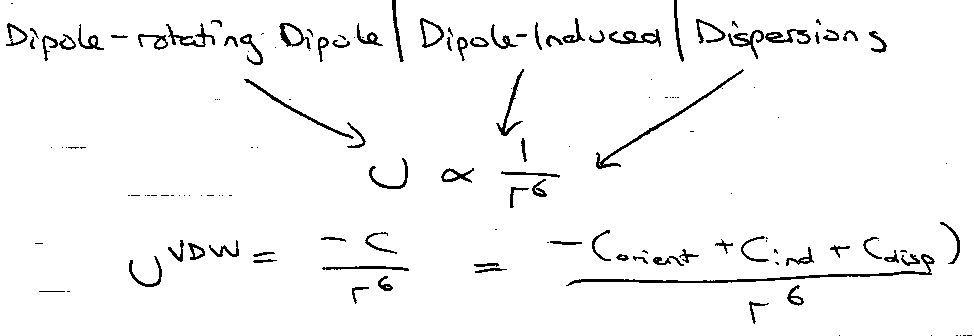
Dipole-Rotating Dipole
Dipole-Induced Dipole
Dispersion
Quadrupolar	Short range
Van der Waals Repulsion	[ Buckingham ]  [ Lennard-Jones ]
H-bonding	Short range

Microscopic Interactions

Coulombic Force –

Polar Molecules

In the limit r2 >> l2, treat molecule as point dipole.

Inductive Interactions

There are several types of dipole interaction.

Charge-Dipole Interactions –

2 Fixed Dipoles –

Rotating Dipoles –

Dipole-dipole: generally << kT.

Free rotation, but Boltzmann Weight, e-U/kT, favour orientations of lower energy.

Thus, average over all possible orientations:

Must be entropically unfavourable to align dipole (ΔS larger when aligned).

Quadrupolar Interactions –

Some molecules have no μ, but quadrupole moment (H) = (for linear charge distribution)

e.g. CO2, benzene.

Compare values:

QUADRUPOLE:

U(r) r-5 (fixed)

U(r) r-10 (rotating)

DIPOLE:

U(r) r-3 (fixed)

U(r) r-6 (rotating)

Also, some molecules neither, e.g. CH4.

Multipoles –

An n-pole is an array of charges with an n-pole moment but no lower moment.

Higher order → weaker.

V(r) 1/rn+m-1 (n-pole to m-pole interaction).

Dipole-Induced Dipole –

Field due to one dipole (~μ/r3) induces dipole in 2nd molecule – 2 dipoles then interact → U ~ αμ2/r6.

Induced dipole, μind = el (i.e. electron’s charge).

Dispersive Interactions

Instantaneous dipole due to asymmetry in electron distribution, therefore exists even in non-polar molecules → U ~ α2/r6.

 Induced-Induced Dipole –

• Acts between all atoms and molecules. Always present.
• Long range.
• Quantum Origin.
• Not a simple power law.

Consider an instance where a finite dipole moment exists because of instantaneous position of electrons.

London Expression for identical molecules:

London Expression for dissimilar molecules:

These forces are Van der Waals –

Hydrogen  Bonds –

Strong, highly directional (linear favoured).

Repulsive Interactions

Overlap electron clouds. For closed shell molecules / atoms, net interaction is antibonding and hence repulsive, e.g. H cations.

Interactions b/w Particles, Surfaces & Particles + Surfaces

Physisorption –

ΔHads ≈ -ΔHvap ≈ -10 … -40 kJ mol-1.

Bound by Van der Waals or dipolar forces (weak, but long range).

Physisorbed molecule retains identity.

e.g. noble gas on any solid, stable gases on salts, oxides, silicates (some exceptions).

Molecules diffuse and rotate rapidly at rtp.

Chemisorption –

ΔHads ≈ -100 .. -400 kJ mol-1.

Strong interactions between adsorbate and solid, normally leads to some kind of chemical bond formation.

• Chemically selective.
• Surface catalysts.
• Adsorption essentially irreversible at rtp.

e.g.

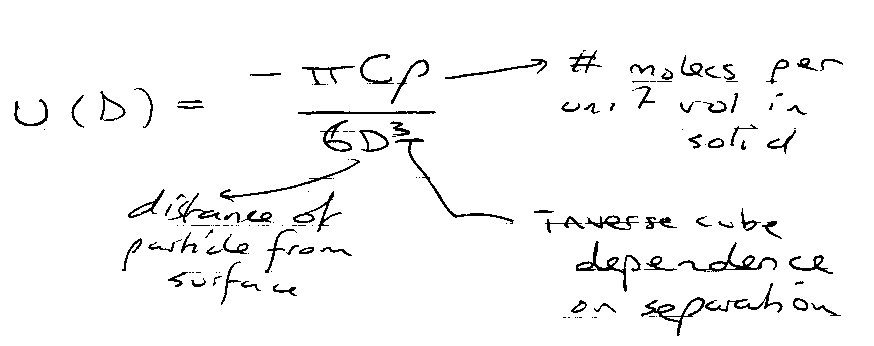
Molecule-Surface Interactions

Assume purely attractive, and additive.

Total interaction:

Total interaction between Molecule and Solid:

Surface-Surface Interactions

Molecule in slab 1 interacts with all of slab 2 as:

Interaction between sheet of thickness dx in slab 1:

Therefore total interaction between slabs:

Total Interaction Energy per unit area between 2 flat surfaces:

Surface & Sphere:

Sphere-Sphere:

The Hamaker Constant

A12 = π2Cρ1ρ2

NOTE: A > 0 means attractive force.

Hamaker Constants usually fall in the range (0.4-4) x 10-19 J.

Interaction between 2 dissimilar particles related to interaction between identical particles:

A12 ≈ √(A11A22)

Particle-Particle Interactions

Important in Colloids – “a dispersed phase distributed uniformly in a finely divided state (1nm – 1μm) in a dispersion medium”.

• fog, smoke, foam, milk, ink, stained glass.

Interaction between 2 particles in a dielectric medium:

Interaction between identical particles always attractive:

A131 ≈ A313, i.e. 2 droplets of water in fog = 2 air bubbles in foam.

Summary:

• interaction between identical molecules always attractive (A > 0).
• If medium 2 has same properties as 1 & 3 then A123 effectively zero (no interaction).
• For dissimilar particles A123 may be attractive (positive) or repulsion (negative) → dispersion forces can lead to repulsion.

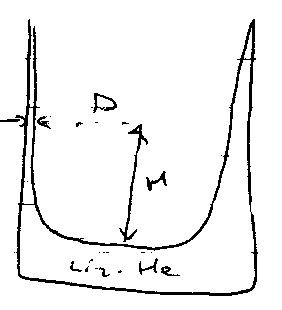
Consequences of Repulsive Interactions –

A123 + AHe,g / He,l / glass < 0.

• Repulsive van der Waals across adsorbed liquid He film.
• Lower energy by thickening film.
• Counteracts gravity.

At equilibrium, dU/dD = 0, → climbs up container.

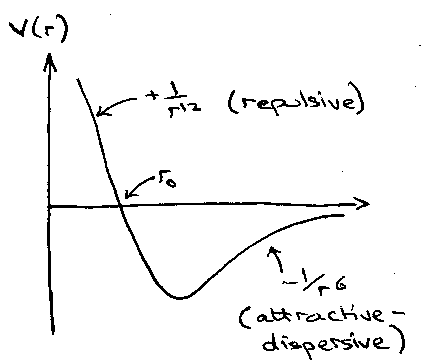
Lennard-Jones Potential –

How measure – van der Waals complexes very weak.

Use Molecular Beam Experiments –

• Transfer momentum in direction of beam.
• Molecules travel at similar speeds, very low translational temperature (supersonic).

Even better → supersonic nozzle – skims off some molecules off jet and results in better defined velocity.

• Trap Van der Waals molecules, few Energy Levels populated.
• Virtually collision-free – no break up of complexes.

Other information –

• Gas imperfections.

B(T) → pairs, C(T) → threes, etc…

Gas Transport Properties –

• Momentum, mass, energy – depends on intermolecular forces.

Shear velocity, diffusion coefficient (pair potential for dilute gas) and thermal conductivity can also be used.

Pair Distribution Function, g(r)

Measures probability of finding another molecule at distance r from reference, ρ(r) = ρog(r)

How measure – diffraction methods.

X-ray Scattering – electrons, increase scattering with atomic number, to locate heavy atoms.

Neutron Scattering – strong Nuclear force scattering by nuclei. Don’t vary much with atomic number, therefore good for locating light atoms.

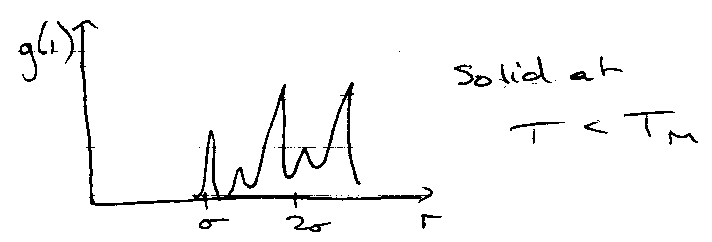
Solid:

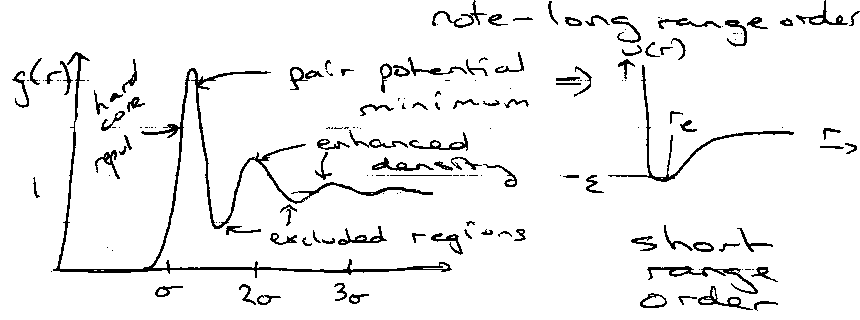
Liquid:

Gas:

Examples –

Ar(l) –

Model as hard spheres. Dispersion forces hold molecules together:

Structure dominated by repulsion between atoms.

CCl4(l) –

Cannot treat as soft sphere. Very high density.

Molecules interlock with neighbours, increasing viscosity and decreasing the diffusion constant.

Atom-Atom Pair Distribution Functions:

H2O(l) –

Hydrophobic Effect – in non-polar medium, need one or more (partial) H2O charges to point to inert solute, i.e. lost to H-bond formation.

→ arrange so that least number of tetrahedral charge point towards non-polar molecule but towards water phase, i.e. H-bond formation.

All H-bond sites can be active if non-polar molecule is not too big. Reorientation of water molecules in cages. But this orders water molecules, so process is entropically unfavourable.

Presence of non-polar molecules makes neighbouring molecules more ice-like (increased H-bonding, decrease entropy).

Consequences:

• Detergents congregate around dirt particles.
• Membranes (polar heads, hydrophobic tails).
• Protein folding (hydrophobic side chains buried inside folded protein).

Macroscopic Interactions

Gas Imperfections –

Ideal, pV = nRT

Z, compression factor, = pVm/RT = 1.

Real Gas:

Virial Equation:

At Boyle Temperature, TB, B = 0

Van der Waals Equation:

Principle of Corresponding States –

Molecules that interact through a pair potential of the same form will have the same equation of state in “reduced” variables. Such systems are said to be “conformal”.

Potential Well –

At the minimum,

Well depth at r = r0:

Assumptions –

• Ignore interactions beyond inner layer.
• Ignore 3 body interactions.
• Ignore interactions in gas phase.
• Inadequacy cf. Lennard-Jones.
• Close packing assumed.

Lennard-Jones Potential (again!) –

ε = well depth, σ = collision diameter.

Principle of Corresponding States works well at near critical temperature, where dispersion dominates (low ρ, high thermal E).

At triple point, short-range interactions are important. For liquid, Vm,c ~ 3 x Vm,t

Also, some interactions are not pairwise additive. This means,

• This applies to fixed charges (crystals).
• Dipole/induced are non-additive.
• Dispersions are weakly non-additive.
• H-bonding is highly non-additive, cf. H2O(l) and H2O(g).

Condensed Phases –

Gas → Liquid via Tb – attractive, Van der Waals. Boiling Point of simple Van der Waals liquid:

Vm,g/Vm,l ~ 300.

ΔSvap ≈ R ln 1000 ≈ 7R.

ΔHvap = ΔUvap + p ΔVvap ≈ ΔUvap + RTb.

In simple liquids, max nearest neighbours is 12. Minimum in pair potential is U = -ε, then:

ΔUvap ~ 6ε

At normal boiling point:

Liquid → Solid via Tm – short-range interactions. Repulsive forces. Specific interactions become important.

Mixtures of Non-Electrolytes

Reminder:

Ideal Behaviour –

Molar Free Energy:

Separate components,

Mixing,

Also for ideal, ΔVmixi = 0.

Non-ideal Mixtures

As x → 1, solvent obeys Raoult’s Law.

As x → 0, solute obeys Henry’s Law, pB = KBxB(l)

Gibbs-Duhem Equation

Chemical Potentials of the components in a mixture cannot vary independently.

Open system,

Integrate at constant μj:

Compare (1) and (2):

Example –

Binary Mixture. Component 1 obeys Raoult’s Law over certain range of composition. Show that component 2 obeys Henry’s Law over this range.

Gibbs-Duhem:

x1dμ1 + x2dμ2 = 0

Vary x1 at constant T and prot:

Assume vapour ideal:

Sub (2) and (3) into (1):

Simple Non-ideal Mixture –

2 components, A and B. ΔSmix ideal – no association or preferred orientation.

Each molecule interacts with Z neighbours through pair potential with average E (ΔVmix=0). Each A surrounded by, on average:

ZxA molecules of A

ZxB molecules of B

If β < 0 – mixing exothermic. Liquid miscible in all proportions.

If β > 0 – mixing endothermic. Behaviour depends on β.

For dispersions,

Effect of β on Phase Behaviour:

T-dependence –

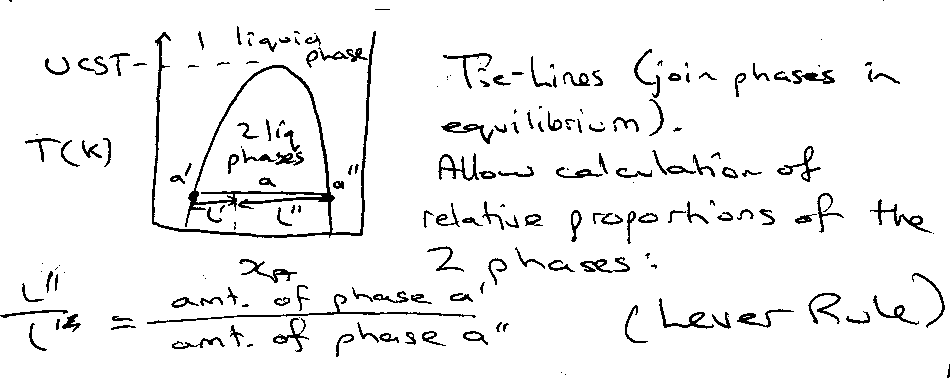
The minimum temperature at which the mixture is miscible in all proportions is the Upper Critical Solution Temperature, Tc.

β = 2RTc

Temperature-Composition Diagram –

Phase Rule –

P + F = C +2

P = number of phases.

C = number of independent components.

F = number of degrees of freedom, i.e. number of variables (T, p, μj …) that can be varied independently.

e.g.

• 1 component & 3 phases, F = 0. Therefore triplet point (T, p fixed).
• 1 component & 2 phases, F = 1. Therefore solid-liquid and liquid-gas equilibria are lines in phase diagram ( p = f(T) ).
• 2 components & 1 phase, F = 3. Therefore at constant T and p, μA can vary.
• 2 components & 2 phases, F = 2. Therefore at constant T and p, μA ad μB are fixed (and so are xA and xB as a result).

Vapour Pressures –

Ideal vapour,

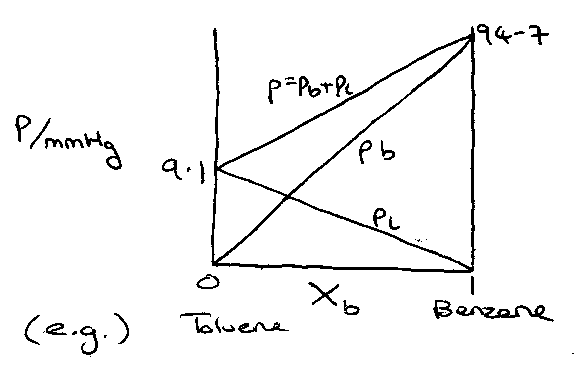
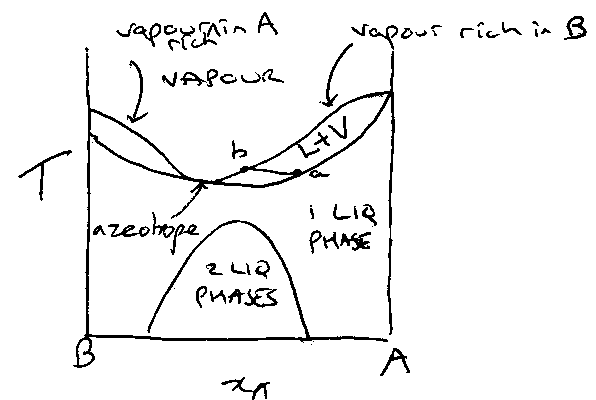
Pressure-Composition Diagram

X = 0.38 → liquid and vapour have same composition, this is AZEOTROPIC.

Liquid at a is in equilibrium with gas at b.

System at c consists of liquid with composition c’ in equilibrium with vapour of composition c’’.

Lever Rule gives relative amounts.

Temperature-Composition Diagram

• Minimum boiling point occurs at azeotropic composition.
• Liquid at a is in equilibrium with vapour of composition b.

Fractional Distillation

From c, cannot generate pure B (get azeotropic composition “d”).

Eutectic Point – temperature at which solid/liquid equivalent of azeotropic (vapour/liquid).

Ions in Solution

Born Equation:

Ion is a sphere, radius a. Charge sphere from q = 0 to q = Ze (self-energy of ion).

Therefore salts dissolve in media of high dielectric constant, ε, but not in media of low ε.

Ions are stabilised by charge-dipole and charge-induced dipole interactions.

Born used a continuum model → not correct in detail for aqueous solution.

Consider structure of water nearest the ions – neutron scattering.

If the water molecules are strongly coordinated to the ions (e.g. Al3+, Ni2+) there are sharp, well-resolved peaks in the pair distribution function and the hydration number is well-defined (e.g. 4 for Be2+, 6 for Al3+).

If water molecules are weakly bound, peaks in g(r) are broader and weaker.

In water, H+ is always found as H3O+, never as a free proton. The predominant species is believed to be planar H9O4+.

Conductivity – very, very high. Relay mechanism – it is INCORRECT that there are concerted proton “hops”, in fact a series of uncorrelated single proton hops is more likely.

Extent of hydration increases with increasing charge and increasing ionic radius. As a consequence, cations are more strongly solvated than anions.

DeBye-Huckel Theory

Treatment of interactions between ions in solution directly analogous to diffuse double layer.

ASSUMPTIONS:

• Central ion of radius a. Other ions point charges (no allowance for finite counterions).
• Ions move in average potential due to all other ions (no ion correlation).
• Purely electrostatic (no ion pairing).
• Weak interaction: Zeφ / kT << 1 (best for univalent ions).
• Continuous, structure-less solvent with uniform dielectric constant (ignores salvation shells, dielectric saturation).

METHOD:

Solve Poisson-Boltzmann equation in spherical polar coordinates.

SOLUTION:

Average distance to counterion = rD.

DeBye Length → “thickness” of ionic atmosphere.

Self-energy absent of ionic interactions:

, where a = radius of ion.

With ionic interactions,

Lowering of energy due to ionic interactions –

Assuming deviations from ideality are purely electrostatic:

DeBye-Huckel Limiting Law –

Good for I ~< 0.001

Worse for I > 0.01

EXAMPLE 1: Standard Electrode Potential

EXAMPLE 2: Solubility Products