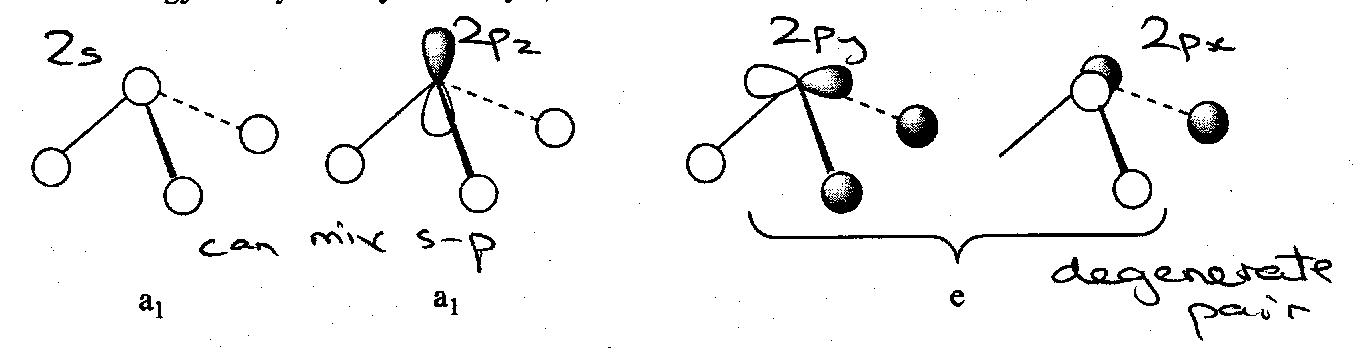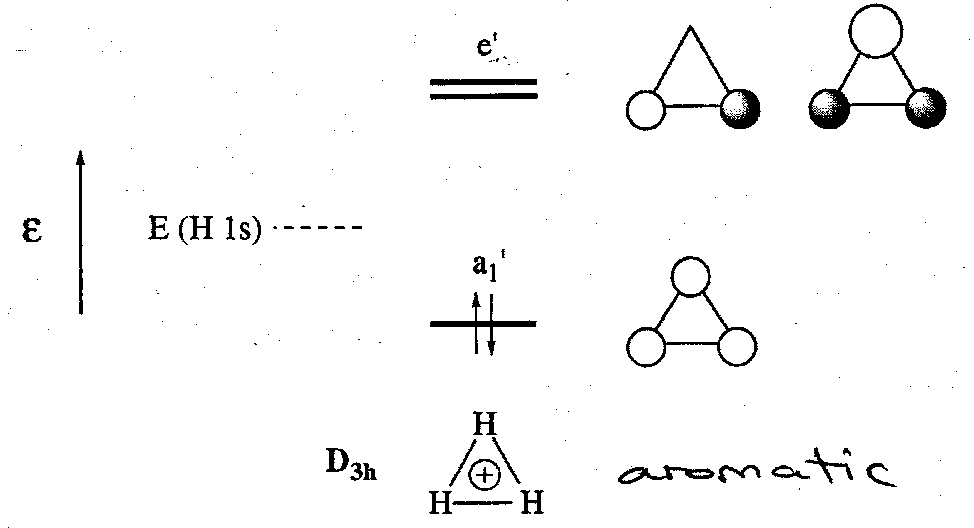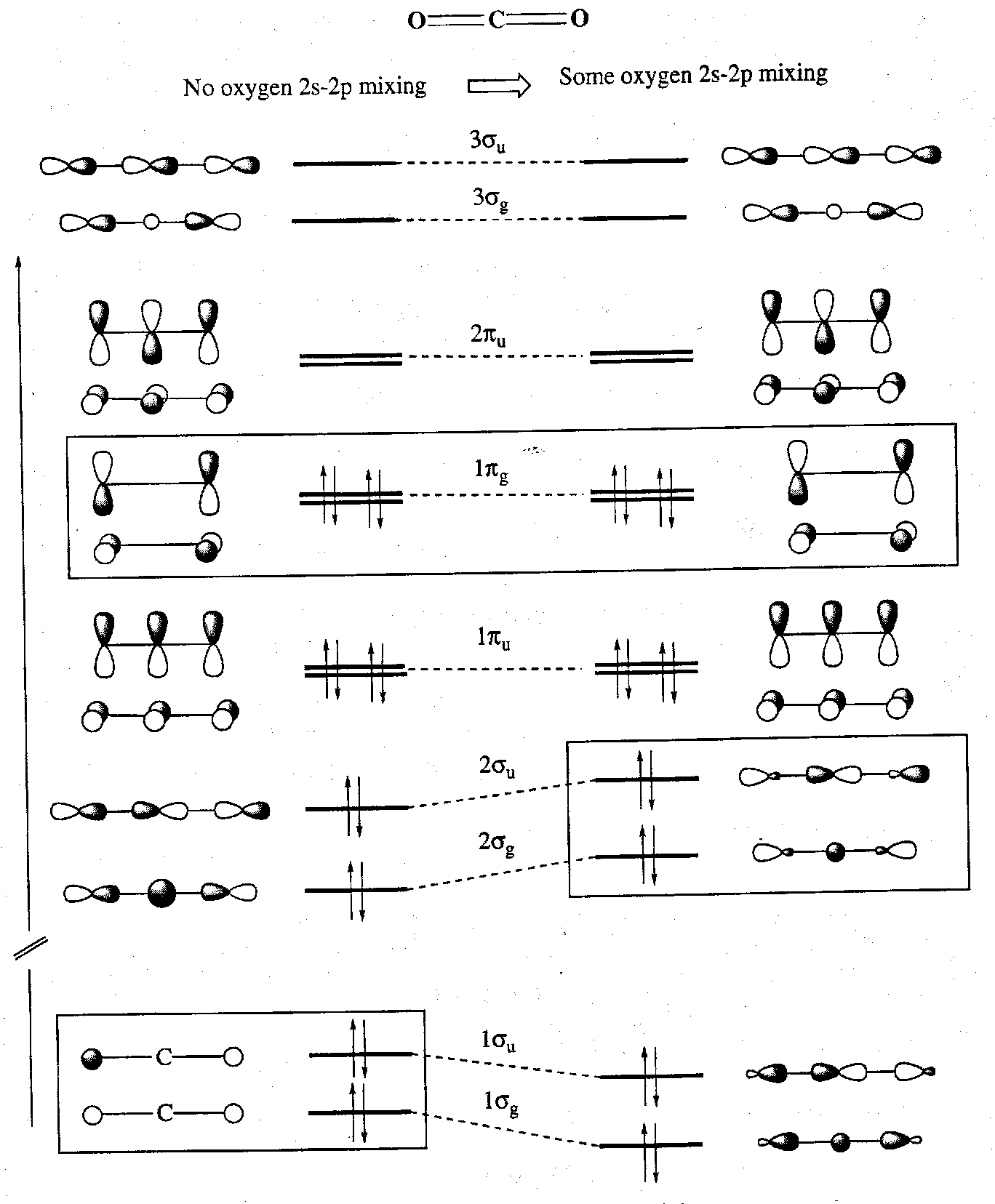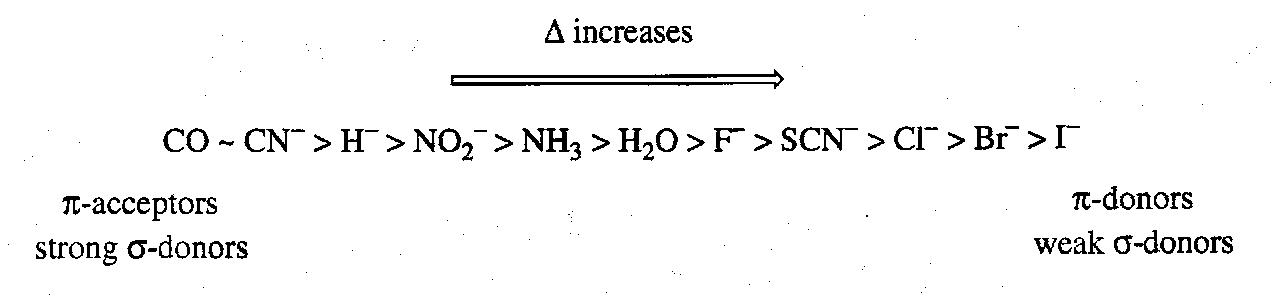Molecular Orbital Theory and Bonding Notes

The Orbital Approximation

In an attempt to handle the problem of calculating a molecular wavefunction, we must break it down somewhat. The most popular approach is to assume that the wavefunction for all the electrons in a molecule can be written as a product of N one-electron wavefunctions. The square of the total wavefunction gives the total electron density in the molecule.

The one electron wavefunctions are molecular orbitals. Clearly a recognition of the nature of these molecular orbitals is part of the key to gaining an understand of bonding in molecules.

The Nature of Molecular Orbitals

“A molecular orbital is the wavefunction of an electron in a molecule moving under the influence of the nuclear attraction and the average repulsion of all other electrons.”

It has the same formulation as an atomic orbital does in a many electron atom. It has an energy associated with it which gives the energy of an electron with such a wavefunction in the field of the nucleus and the other electrons.

The square of the MO gives the probability density for the electron.

MOs are delocalised. An electron wavefunction extends throughout the molecule, and is not confined to a “bond” between two atoms, except in diatomic molecules.

The Linear Combination of Atomic Orbitals approach to Molecular Orbitals

The method of using LCAO, an approach that can be considerably simplified through the benefits of symmetry and group theory, to gain best-guesses of the MOs is crucial to our aim of understanding the bonding in molecules. From this follows all of the consequences for structure, spectroscopy, properties and reactivity. The LCAO approach is a very successful one, especially when more sophisticated versions are implemented.

When an electron is close to the nucleus of one atom, A, its wavefunction closely resembles an atomic orbital (AO), χA, of that atom. We can therefore make a reasonable approximation to an MO by superimposing AOs of each atom in the molecule. This method is known as the LCAO. The coefficients ci represent the contribution of each AO to the resultant MO:

φi = cAχA + cBχB + …

In the simplest form of LCAO theory, only the valence orbitals of the atoms are used to construct MOs (e.g. just the 1s for hydrogen, only the 2s and 2p for carbon, and so on). In more accurate forms of calculation other orbitals are also included. The atomic orbitals used are known as the basis set. In general, the larger the basis set the more accurate the calculations, but the more demanding they are computationally. In general, only the simplest systems can be calculated with a great degree of accuracy.

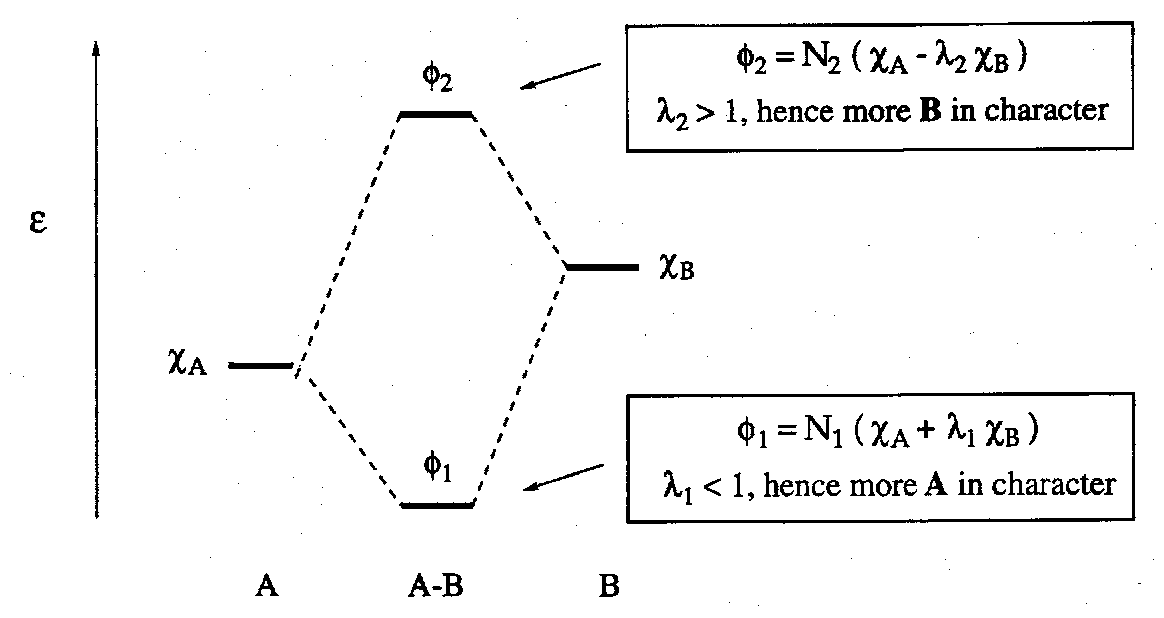
LCAOs are used to construct MOs. If we take two AOs, χA and χB, of energies -εA and -εB respectively, we form two molecular orbitals:

φ1 = N1(χA + λ1χB)

φ2 = N2(χA - λ2χB)

The MOs must form an orthonormal set.

The number of MOs obtained from LCAO equals the number of AO basis functions.

It is obvious that atomic orbitals must overlap in order to combine to form an MO. In other words, the overlap integral SAB between two atomic orbitals must be non-zero. Only orbitals carrying the same symmetry labels can overlap, otherwise SAB equals zero. This is one example of how useful group theory can be in analysing the bonding in polyatomic molecules.

Orbitals which overlap constructively concentrate charge in the internuclear region and are bonding. Orbitals which overlap destructively strip the internuclear region of charge and are antibonding. In general, the greater number of internuclear nodes the higher the energy of an orbital (cf. AOs in the H atom, particle in a box, etc).

The energy of stabilisation of a bonding MO, and the energy of destabilisation of an antibonding MO (wrt combing AOs) depends on the size of overlap and the energy separation of the combining AOs. The energy of stabilisation of an MO is at a maximum when the two combining AOs have the same energy.

The interaction of AOs can be represented on a MO diagram where the respective energies of the combining AOs and resultant MOs are plotted. This is a very helpful approach, especially for polyatomics, since the AO origins of the individual MOs can be readily followed visually.

Once an MO ordering has been established for a particular molecule, the MOs are filled according to the Pauli Exclusion Principle and the Aufbau Principle – just as for atoms. The MOs are occupied with pairs of electrons with opposite spin in ascending energy. There are some further important points that follow from this:

• The same set of MOs may be used for molecules with the same valence AOs but different numbers of electrons. Again the comparison with the treatment of many-electron atoms is evident. An example is the use of the same MO scheme (but with differing orbital occupation by electrons) to qualitatively account for the reduction in formal bond order 2.5 to 1.0 on going along the series: O2+ → O2 → O2- → O22-.
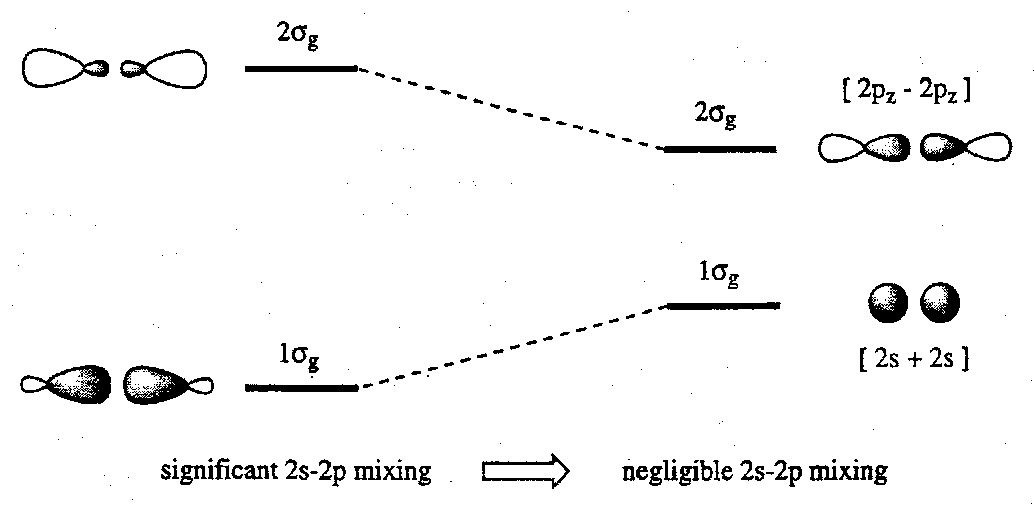
• The order of the MOs may change along a series as the energies of the AOs and/or the overlaps between them change. A good example of this is found for the 1st row diatomics Li2 → F2 in which increasing 2s-2p atomic orbital separation leads to reduced 2s-2pz mixing and consequence inversion of the relative 2σg and 1πu MOs.
• The effect of 2s-2p mixing (ignoring any change in orbital energies) may be represented by:

• The energy of the MOs depends on electron-electron repulsion, and hence on the occupancy of orbitals. This is effectively ignored in simple 1-electron MO schemes.

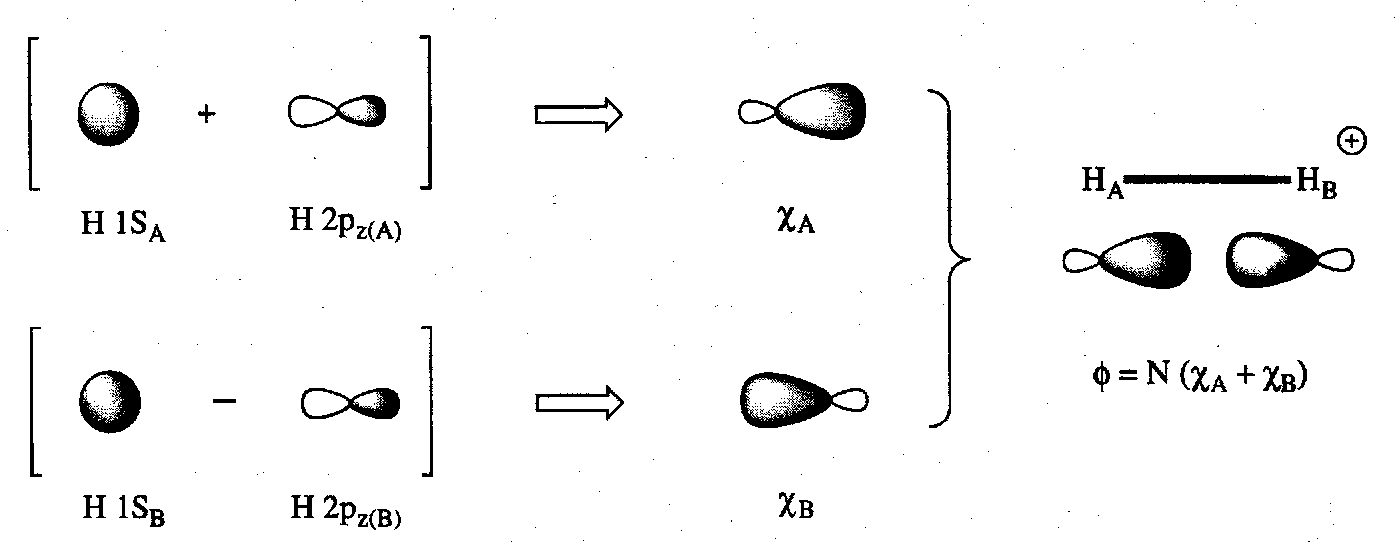
Diatomic Molecules: H2+, H2 and AH

The wavefunctions for H2+ and H2 using an LCAO approach

MO Schemes for AH molecules (A = second period atom, Li to F)

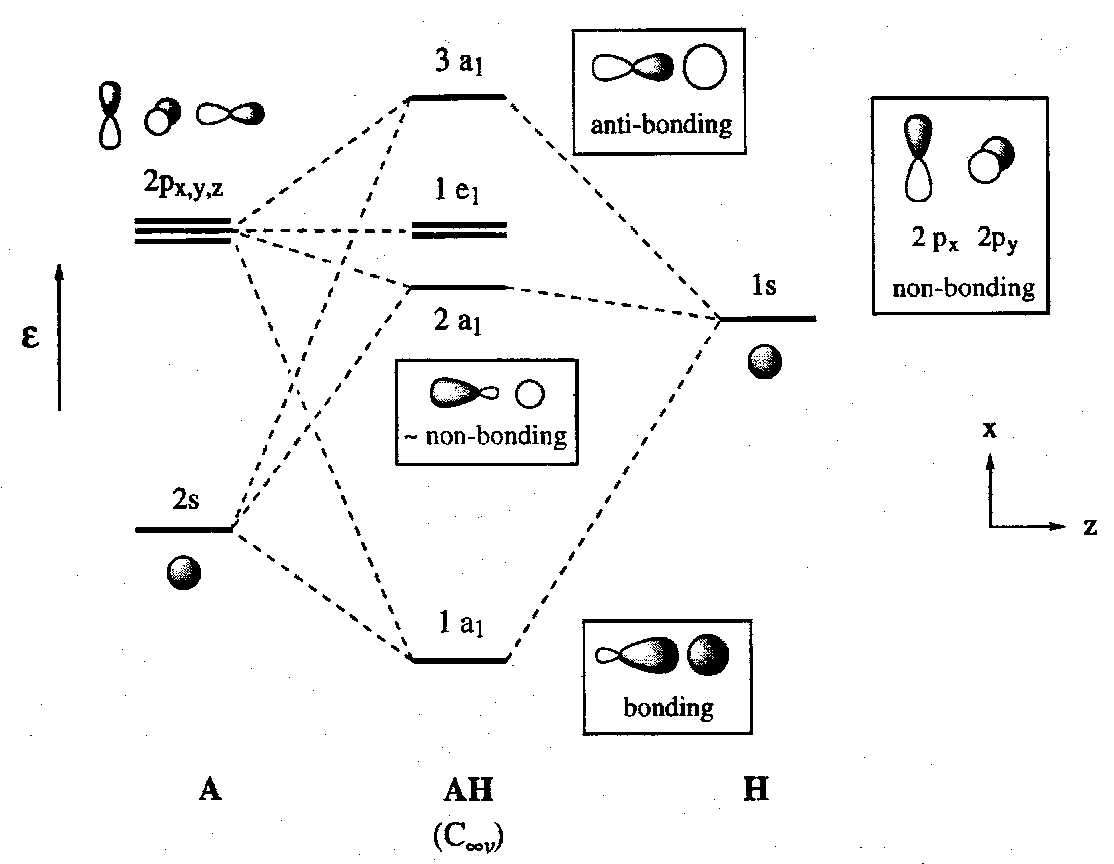
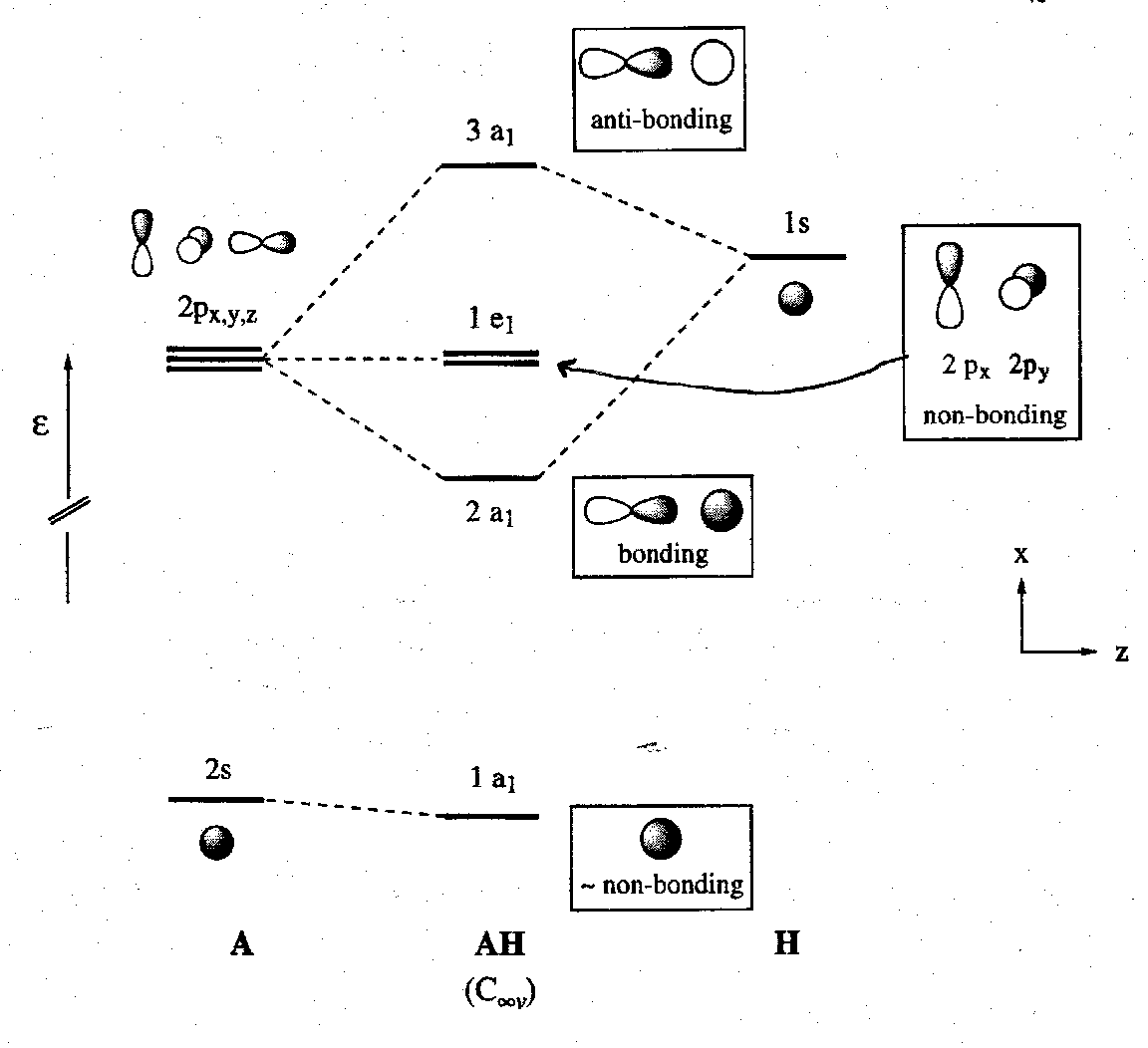
Considering linear diatomic molecules AH. The A atoms have one 2s and three 2p valence orbitals. In such systems it is conventional to take z as the molecular axis.

It is a general result that the exact pattern of MO energies and coefficients varies when three AOs interact. We can distinguish two limiting cases. In both, one σ-bonding, one σ-non-bonding and one σ-antibonding orbital are formed, but the identities of the three MOs vary.

In the first limiting case, both the 2s and the 2pz orbitals of the atom A interact strongly with the H 1s orbital because they are close together in energy and overlap well. Note that this is permitted by symmetry since these three AOs all have a1 irreducible representations in the C∞v symmetry of the AH molecule. 2px and 2py orbitals are strictly non-bonding by symmetry alone since they transform to e1.

In this situation bonding is maximised in the more stable orbital (1a1 level above). The mixing of s and p orbitals in the MO of a molecule is the equivalent of hybridisation in valence bond theory.

In the second limiting case the A atom’s 2s orbital is too low in energy to interact significantly with the 1s orbital. Note that the symmetry analysis for the AH molecule is the same as in the first case, but the atomic orbital make-up is very different in each of the MOs, and the 1a1 MO is almost entirely made up from the 2s atomic orbital of the A atom.

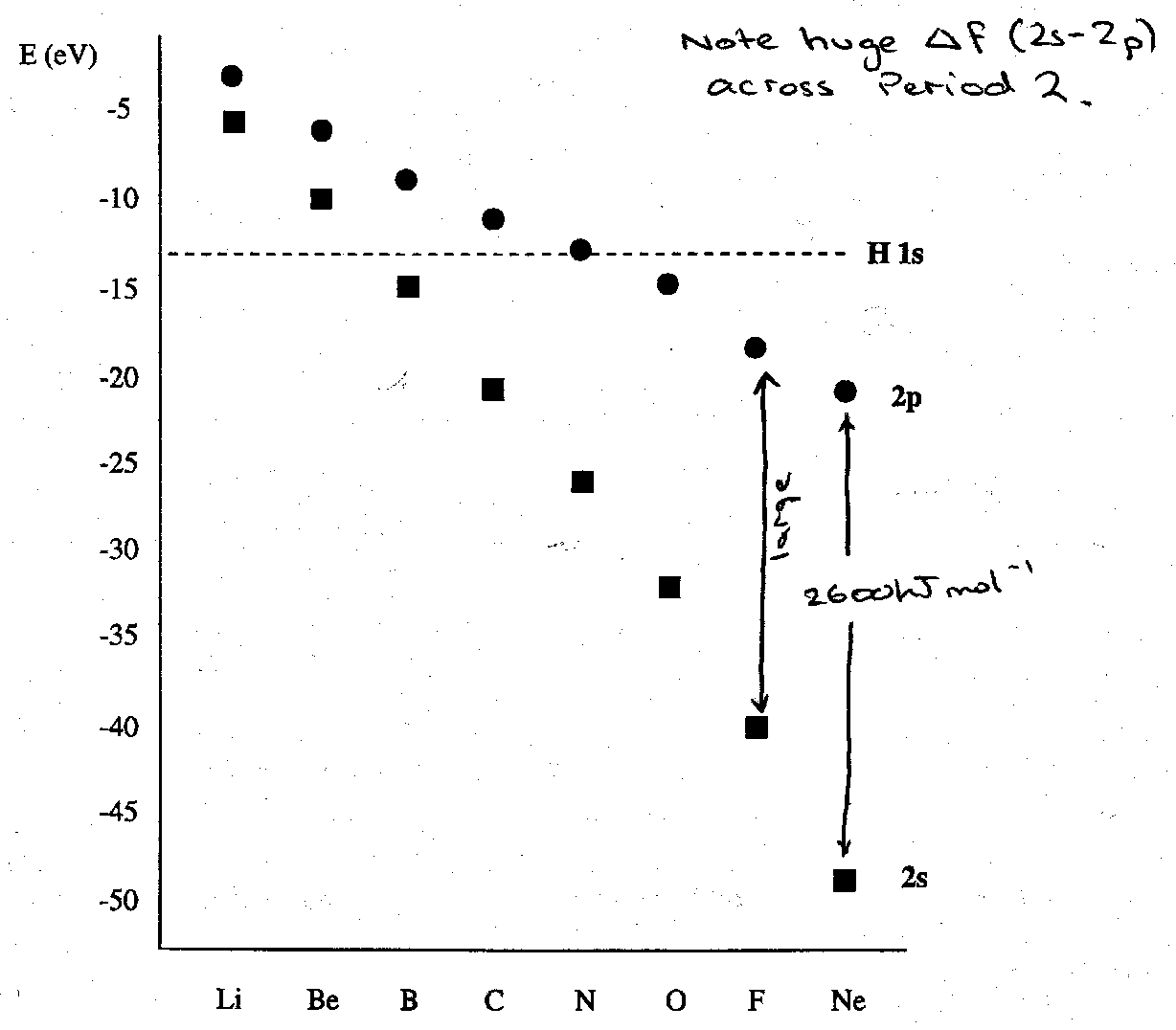
Atomic orbital energies are therefore crucial in determining the MO pattern. If the A atom is very electropositive (Li, Be) the 2s and 2p valence orbitals lie high in energy and above that of the H 1s orbital. If, on the other hand, A is very electronegative (e.g. F) its 2s and 2p orbitals lie lower in energy than 1sH. For elements of intermediate electronegativity, such as B, C and N, the H 1s orbital lies between the A atom’s 2s and 2p levels. In general we expect much more s-p mixing in B and C than in O and F because the energy difference between 2s and 2p levels is not yet prohibitively large.

The valence shell energies are plotted below to emphasise the dramatic effect of the 2s atomic orbital stabilisation relative to 2p. This follows from the differing extents of penetration of the 2s vs. 2p atomic wavefunctions:

Symmetry and MO Diagrams for the first row Hydrides AHn

The Use of Symmetry in Polyatomic Molecules

With polyatomic systems, there are potentially very many AOs to consider, so we expect an equally large number of MOs. However, if a molecule is symmetric, we can still deal with their interactions in a semi-qualitative way.

If two or more atoms are chemically identical, they must be associated with equal electron density. Therefore in any molecule with two equivalent H’s the contribution to any MO in the molecule will be the same. Such linear combination of equivalent AOs is known as Symmetry Adapted Linear Combinations (SALCs).

If we can generate SALCs for equivalent orbitals for molecules just by using symmetry, we pre-fix the relative coefficients of the AOs in the MOs and the interaction between the different atoms is then often reduced to that between 2 or 3 orbital sets.

MO Treatment of AH2 (C2v), e.g. H2O

Group Theory analysis shows that there are 6 MOs possible from the combination of 6 AOs (4 on O and 2 on 2H). 2 of these are bonding and thus 2 are antibonding, and the remaining 2 are non-bonding.

These can be depicted thus:

We can now construct an MO diagram:

In this MO diagram the highest occupied Molecular Orbital (HOMO) is the non-bonding 1b1 level. The lowest unoccupied MO (LUMO) is the 3a1 level.

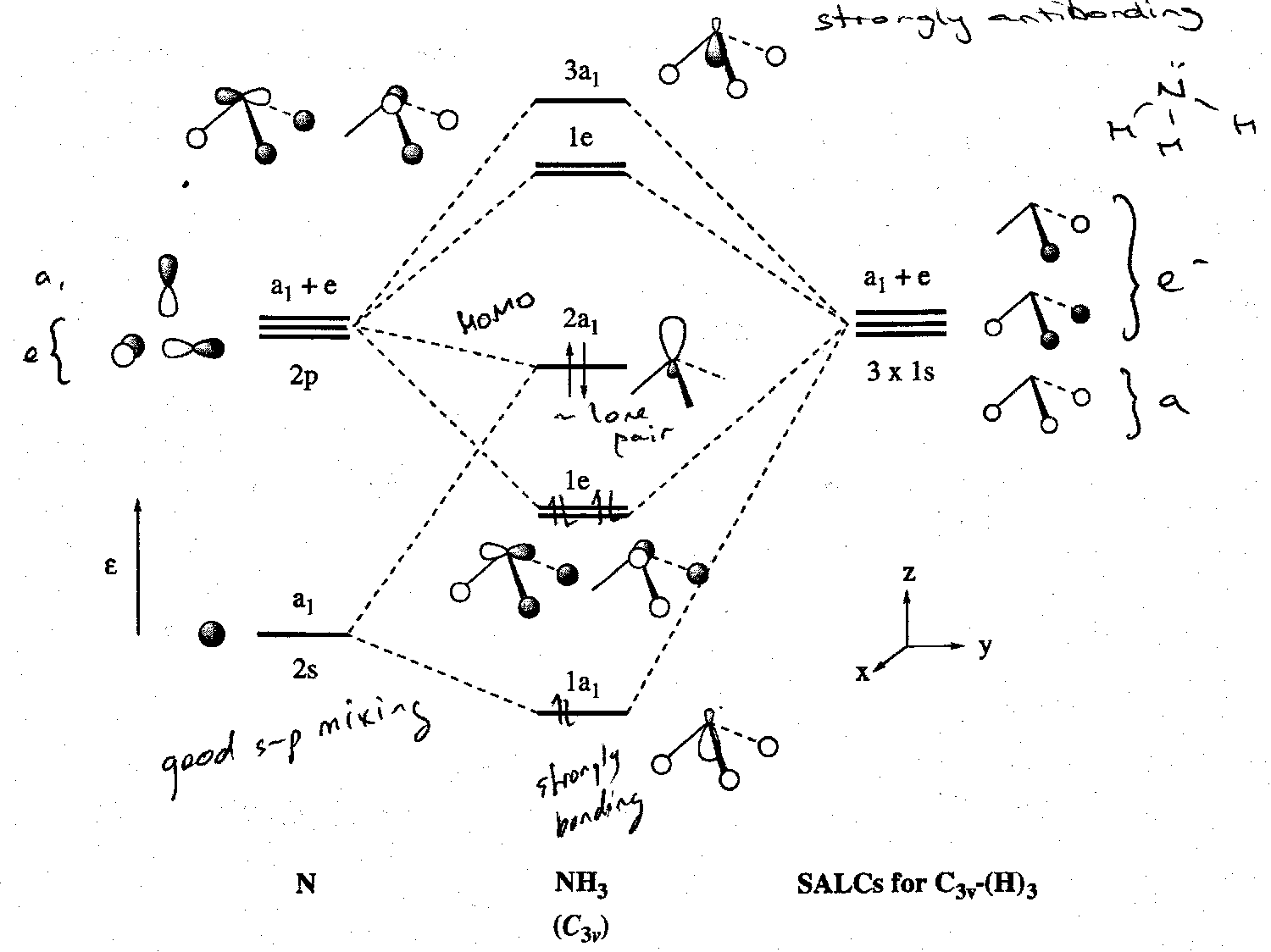
MO Treatment of AH3 (C3v), e.g. NH3

4 AOs on N and 3 for 3H gives 7 MOs to consider. Of these, 3 are bonding and hence 3 are antibonding, leaving 1 non-bonding orbital. These can be depicted thus:

The resultant MO scheme for NH3 is:

Note that there is a fair degree of 2s-2p mixing. In the a1 orbital manifold N-H bonding is well-developed in the more stable orbital (1a1 MO) with 2a1 MO possessing somewhat more non-bonding character. The two electrons in the 2a1 level are the MO equivalent of the NH3 lone pair obtained in valence bond descriptions of the bonding.

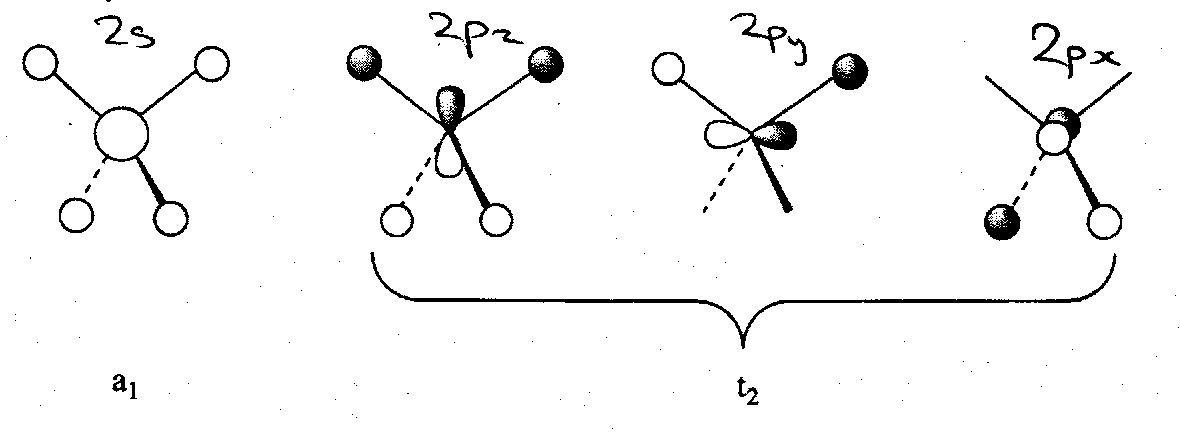
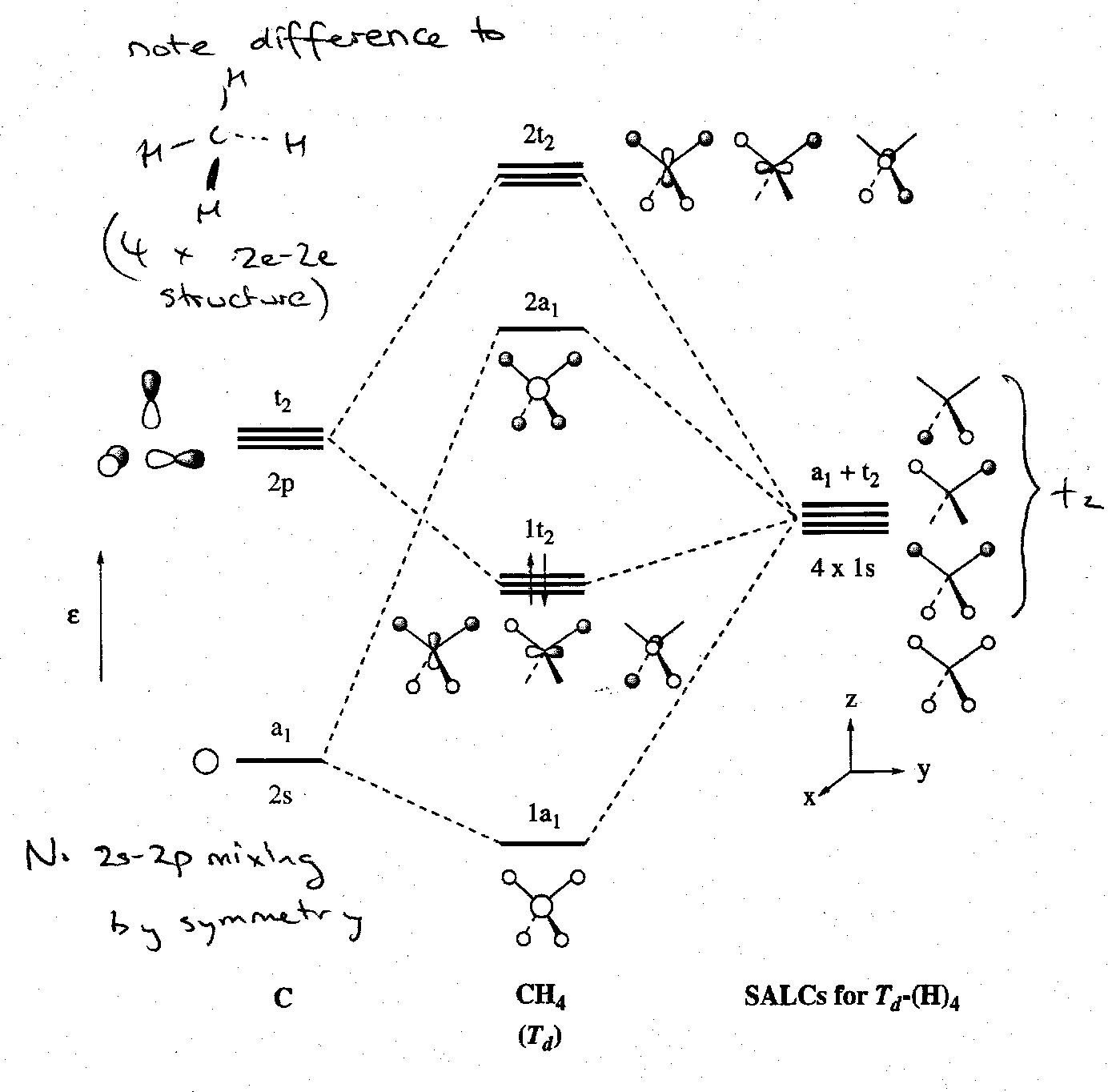
MO Treatment of AH4 (Td), e.g. CH4

We now have 4 bonding and 4 antibonding MOs to consider. This is because all of the carbon AOs have a symmetry match among the H SALCs. This can be depicted as follows:

The MO scheme is illustrated below. Note that although there is a favourable 2s-2p AO energy separation, there is no s-p mixing in CH4 because the 2s and 2pxyz orbitals have different irreducible representations in the Td point group.

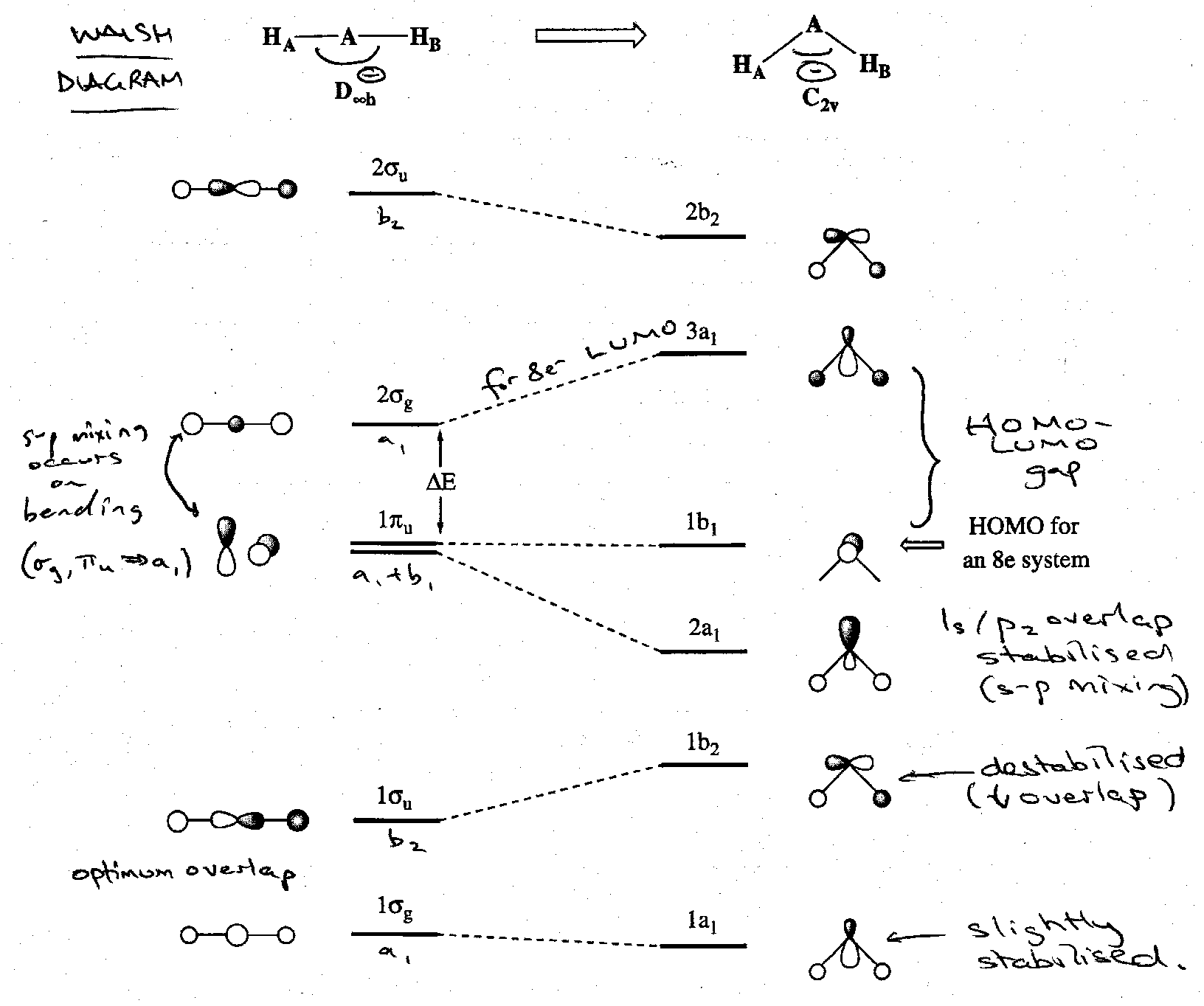
The Use of Walsh Diagrams in Exploring Molecular Shapes

A Walsh diagram is a correlation diagram that portrays the variation in the orbital energies of a molecule as its shape is changed. By selecting the geometry that results in the lowest total energy (which is approximated as the sum of the orbital energies) it is possible to predict the likely shape of a molecule from the occupation of its orbitals and also from their relative energies. Walsh’s rule for predicting molecular shapes stated:

“A molecule adopts the structure that best stabilises the HOMO. If the HOMO is unperturbed by the structural change under consideration, then the occupied MO lying closest to it governs the geometric preference.”

Another general “rule of thumb” is that molecules tend to adopt the geometry that maximises the HOMO-LUMO gap.

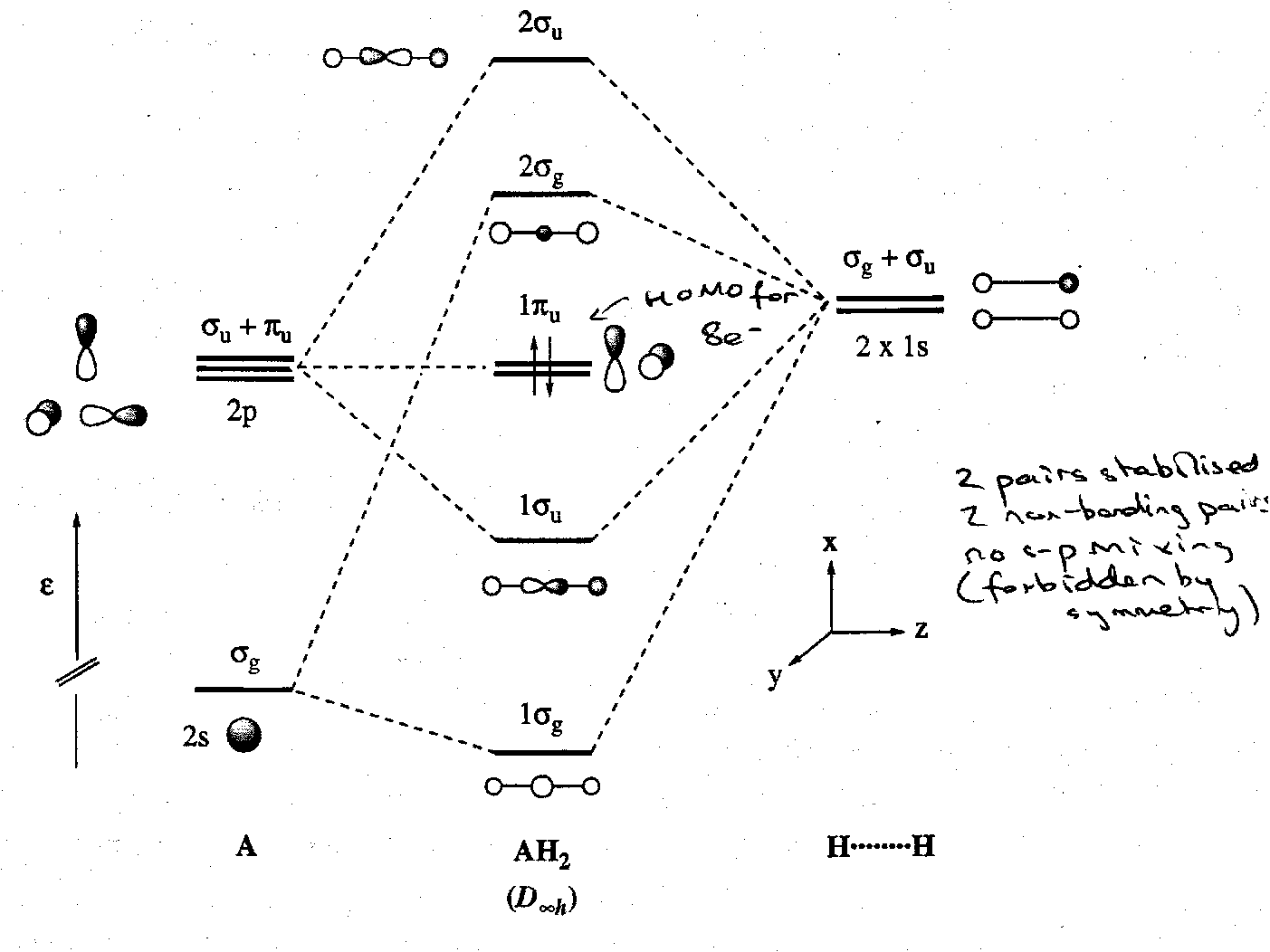
The Shapes of AH2 molecules

MO schemes for two alternative structures are set up and the orbital energies of the two are correlated.

Consider the case of a general AH2 molecule. It can have either a linear (D∞h) or a bent (C2v) structure. We already have an MO scheme for a bent AH2 molecule such as water. A linear one is readily derived. In a linear geometry with z as the molecular axis, the A 2s and 2pz orbitals are the only ones that can combine with the SALCs for two H atoms. Hence:

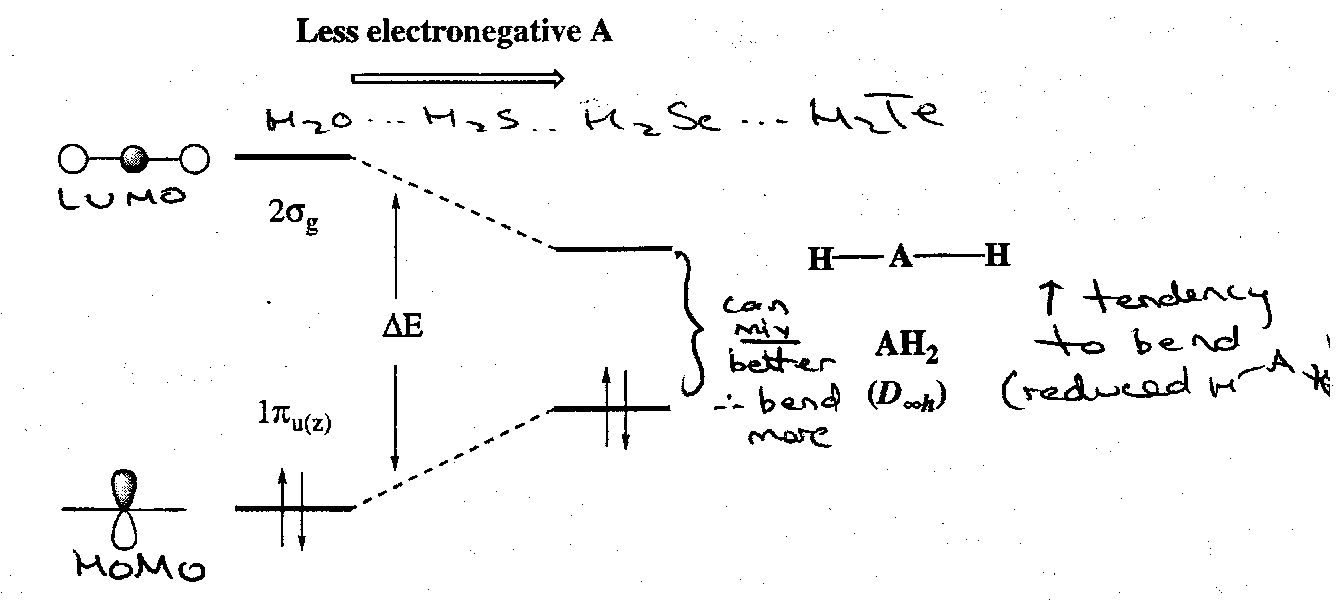
The exact form of the Walsh correlation diagram for AH2 (see below) is disputed. However, all agree on the essential features of the change in energies of the 2a1 and 1b2 orbitals on bending. The 2a1 orbital drops in energy on bending as the originally non-bonding 2pz orbital can now overlap with the H 1s orbitals, and it also mixes with the 2s orbital. The 1b2 (bonding) orbital becomes less stable as the H-A-H angle is decreased from 180o because the 2py orbital no longer points directly at the H atoms and so overlap decreases.

It is important to emphasise that it is the reduction in symmetry that allows the mixing of the 2s and 2pz orbitals of the central A atom. In the lower C2v symmetry the 2s and 2pz AOs both transform as the symmetry a1 and can mix. This effectively results in the mixing of the 1σg and 2σg MOs of linear AH2 with the pz component of the πu non-bonding set. It is the 2σg MO that mixes best with the 2pz component of the 1πu MO because the energy separation between these two MOs is much smaller than between them and the 1σg MO.

The principal feature that determines whether or not an AH2 molecules is bent or not is whether the 2a1 orbital is occupied. This orbital has a much lower energy in the angular molecule than the linear one. Hence, when the 2a1 orbital is occupied, a lower energy is achieved if molecule is bent. The shape adopted by an individual AH2 species depends on:

• Primarily the number of electrons in the valence orbitals.
• Secondly the energy gap ΔE between the 2σg and 1πu MOs (this governs the extent of s-p mixing and the extent of stabilisation of the 2a1 MO on bending).

Known shapes of some AH2 molecules are summarised in the following table.

Known Shapes of some AH2 molecules
Molecular Species	# valence electrons	Shape
LiH2+	2	Bent
LiH2	3	Linear
BeH2	4	Linear
BH2	5	Bent
CH2	6	Bent
NH2	7	Bent
OH2	8	Bent

For three or four electron species the molecules are linear as this results in a more stable 1b2 orbital. For more than four electrons the molecules are bent as the 2a1 orbital is then occupied and this orbital changes the most (i.e. stabilises) in energy with angle.

Molecules with just one electron in the 2a1 orbital have significantly larger H-A-H angles than those with two. Remember that to bend the molecule destabilises the b2 electrons. With two electrons in the 2a1 orbital there is more stabilisation on bending than with just one. Occupation of the b1 orbital, which is non-bonding in both the linear and bent configurations, makes less of a difference to the angle.

The energy gap between the orbital decreases with decreasing electronegativity of the atom A (e.g. down Group 16):

This is because:

• The antibonding 2σg level becomes less antibonding (so is stabilised) as the ns atomic orbitals of A become more diffuse on descending the group.
• The non-bonding 1πu(z) MO becomes less stable as electronegativity decreases and principal quantum number increases.

Therefore as ΔE decreases, the mixing of the 2σg and 1πu(z) MOs increases, giving a more stable 2a1 level and so greater driving force for bending.

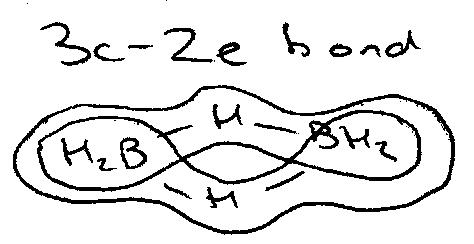
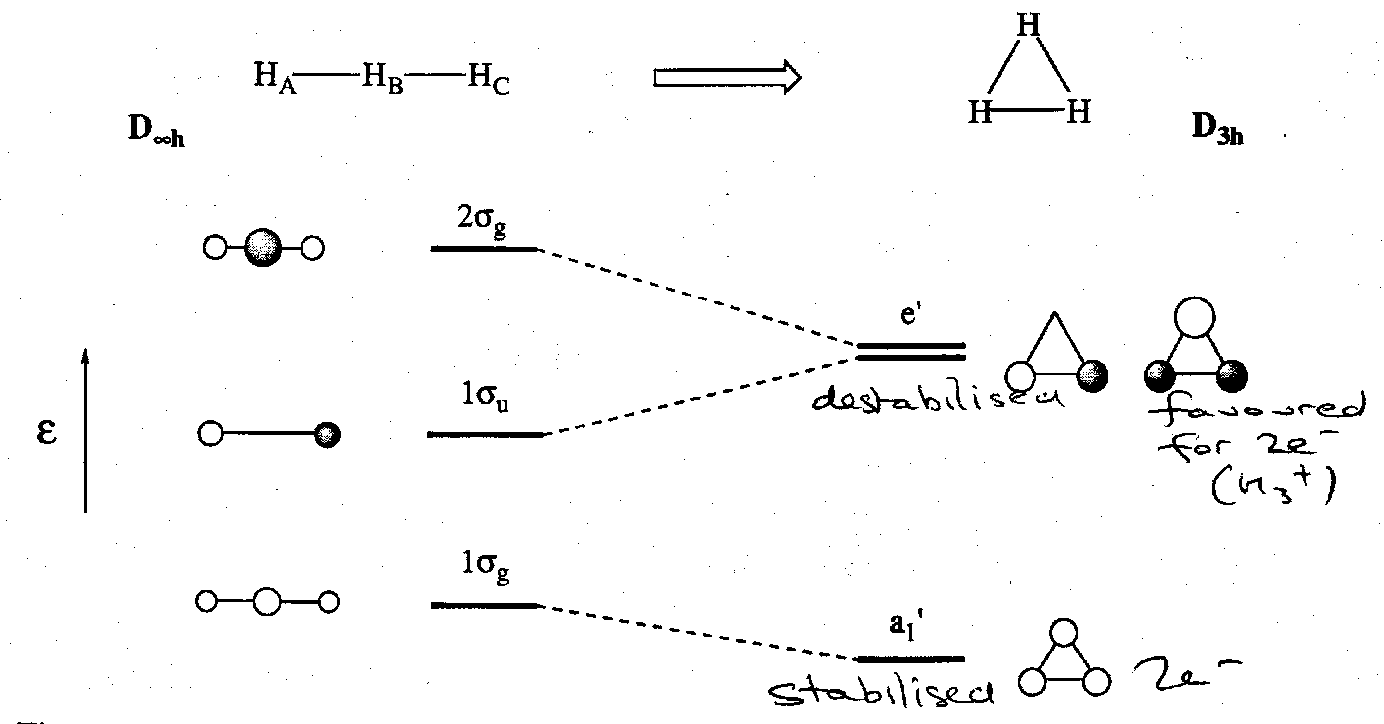
The Shapes of H3+ and H3- : 3c2e and 3c4e bonds

The molecules so far considered are typical ones which involve traditional ideas about electron pair bond formation. This is however not always the case, e.g. borane, B2H6.

Walsh diagrams can be used to explore the molecular structures of H3+ and H3- and analyse 3-centre 2-electron and 3-centre 4-electron bonding.

The principal shapes for H3+/- are triangular (D3h) and linear (D∞h). The SALCs of triangular H3+ are easily derived from the three H 1s AOs. They combine to give three MOs:

The H3+ ion has been observed by mass spectrometry. The bonding orbital a1’ accommodates the two electrons and the overall electronic structure can be described by a 3c2e bond. The H3+ ion is thermodynamically stable wrt H+ (g) and H2 (g). The enthalpy for this process is comparable to the H2 bond itself. This shows how important delocalisation of electron pairs is for producing stability in molecules.

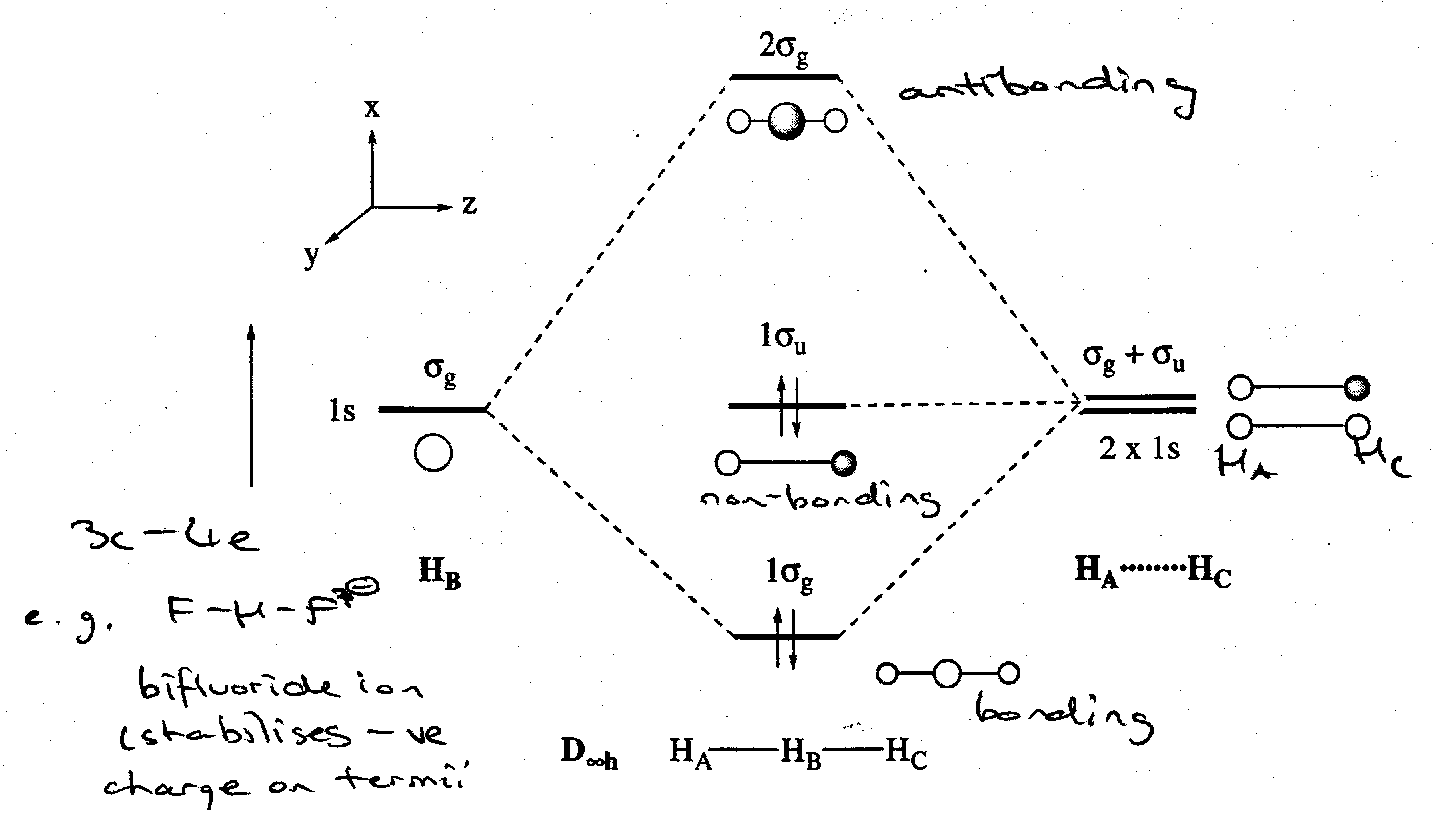
The SALCs of linear H3- can be constructed using a fragment orbital approach, as usual. In this case the two outer hydrogens (σg + σu) combine with a central H atom (σg), in an analogous manner to a linear AH2 molecule, although obviously the central H does not possess valence p orbitals.

The situation in H3- is usually described as 3c4e bonding. H3- is the simplest example of this quite widespread model. The “surplus” two electrons are accommodated in a H--H non-bonding MO (1σu) localised on the terminal H atoms.

Knowing why H3+ has a triangular structure but H3- has a linear one can be explained by using a Walsh Diagram. It is seen that for 4 electrons the linear structure is favoured but for 2 electrons the triangular one gives the best electronic stabilisation:

Molecular Orbital Descriptions for Hypervalent Molecules

Bonding in XeF2

This is one of the simplest examples of a post-transition metal hypervalent compound. Xe atoms have 8 valence electrons in 5s and 6p orbitals (full octet) while each of the terminal F atoms provides (in a Lewis picture) a further electron to the bonding. Hence the Xe atom has 10 electrons around it. This can be rationalised by considering resonance forms of F- and +Xe-F. This suggested delocalised bonding with an average XeF bond order of 0.5. This can just about be rationalised by valence bond theory by invoking the use of 5dz2 orbitals on Xe (although these are very high in energy).

An MO description is best developed by first considering CO2, which has the same symmetry analysis (except that XeF2 brings np valence AOs as well as the ns AOs).

CO2 possess 16 valence electrons, and these form a framework of σ and π bonds like so:

It is seen that whether or not s-p mixing is taken into account affects the results. In both descriptions however there are 8 filled MOs: 2 σ-bonding, 2 π-bonding, 2 σ-non-bonding and 2 π-non-bonding.

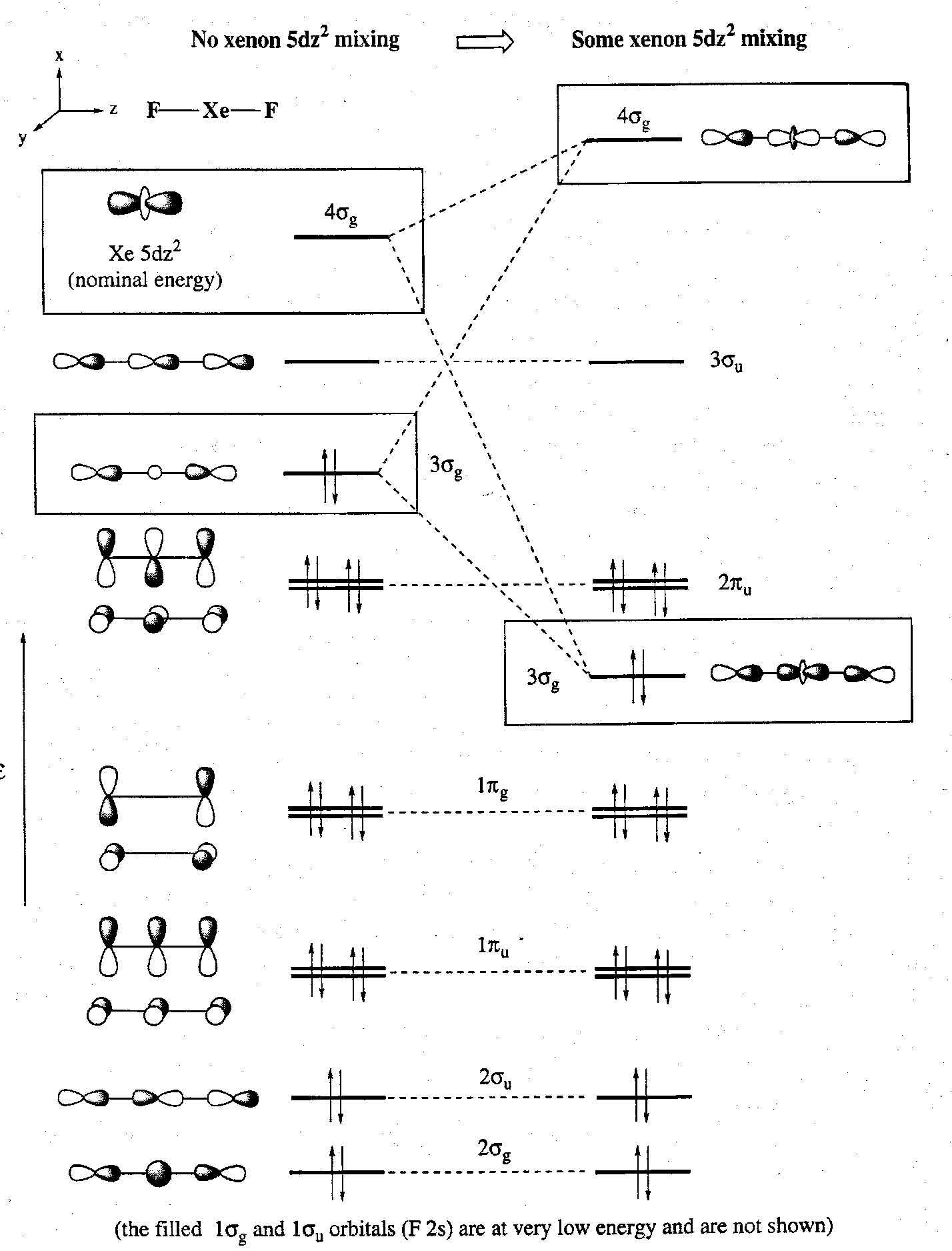
An approximate XeF2 MO description is shown below. The left hand side shows it without and 5dz2 contribution, while it is included on the right, where mixing with the 3σg MO stabilises the two electrons in that orbital. Antibonding character subsequently builds up in the new 4σg MO.

The 2s AOs of fluorine lie very low in energy and so they do not participate significantly in Xe-F bonding (i.e. no mixing, unlike in CO2).

XeF2 has 22 valence electrons (8 from Xe, and 7 from each F) to be accommodated in this MO scheme. Without the 5dz2 contribution this requires the MOs to be filled up to and including the 3σg level. Thus gives 11 filled MOs. This leaves only 1 antibonding MO unoccupied, compared to 4 in CO2. In XeF2 therefore the Xe-F bonding can be considered to be based on a net 3c4e interaction derived from the σu manifold.

The symmetry-allowed mixing in of the 5dz2 AO would have a stabilising effect by adding some bonding character. It is not clear, however, to what extent this orbital mixing actually occurs, if at all. The 5dz2 AO is expected to lie fairly high in energy relative to the 5s and 5p AOs, although the electron withdrawing effects of the F atom will generate a partial positive charge on Xe that would to some extent stabilise this orbital.

The key conclusion is that the bonding in XeF2 can be described without d-orbital participation (i.e. delocalised 3c-4e bonding). Any stabilisation by 5dz2 will not be to the same extent suggested by a formal sp3d hybridisation model.

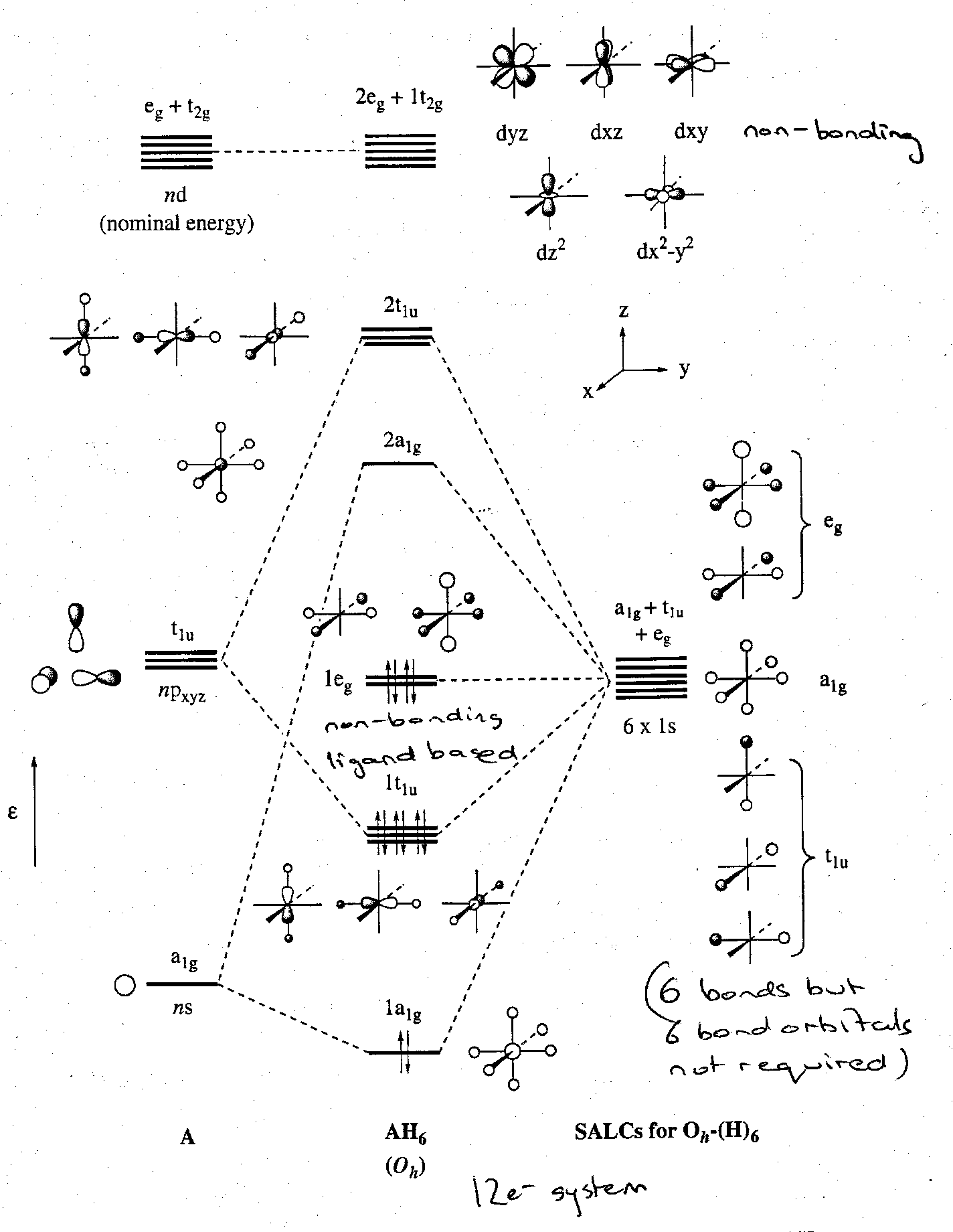
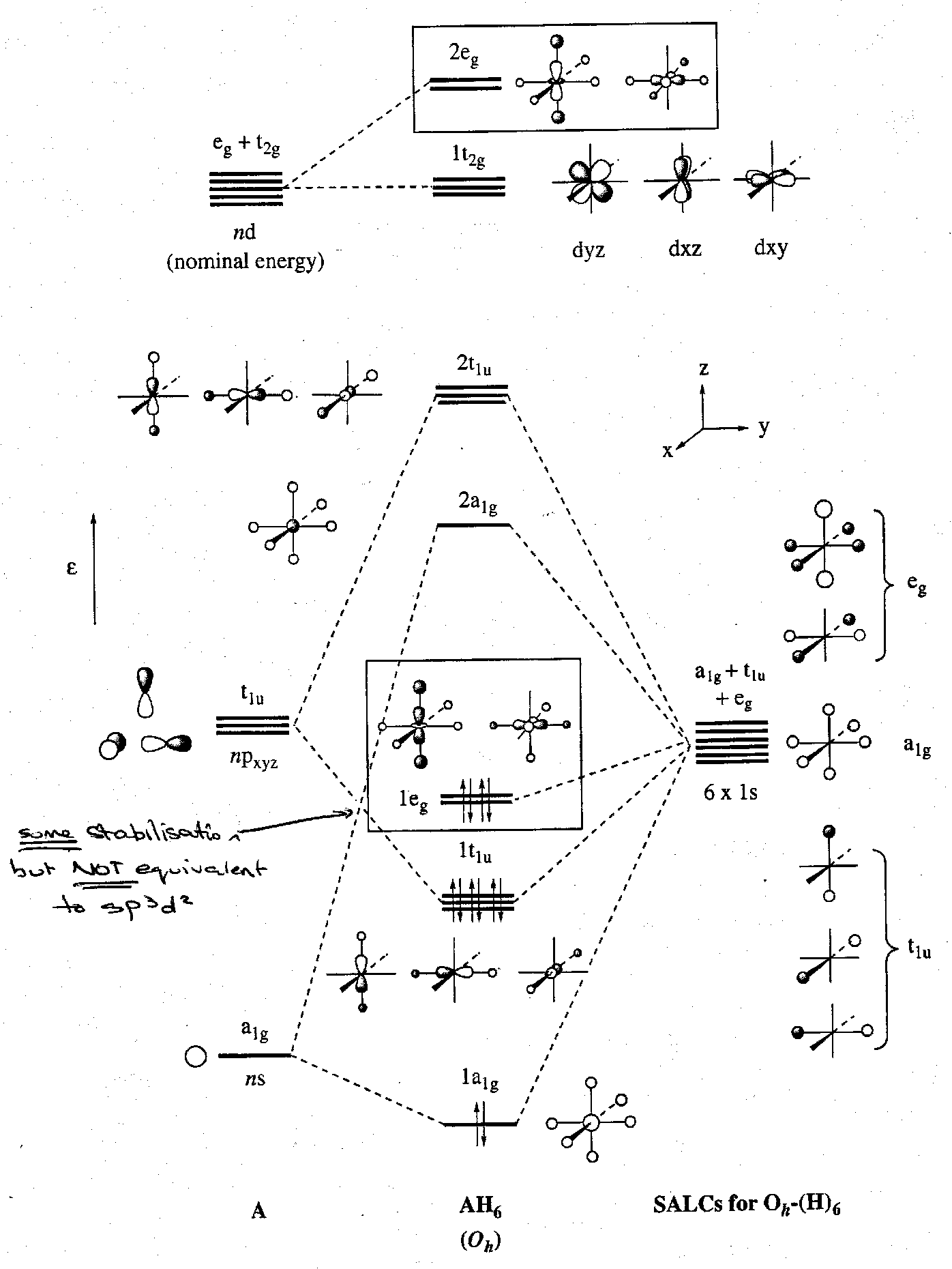
12-electron Main Group Octahedral Systems: SF6 as an example

This is another hypervalent complex, which has 12 valence electrons. As for XeF2, molecules such as SF6 have more than 8 electron pairs around the central atom and so satisfactory Lewis octet structure require a series of resonance forms. As with XeF2 hybridisation can be invoked (sp3d2) to allow for 2c-2e bonding. This again requires the use of high energy 3d orbitals (on S), so it is unlikely that this is valid.

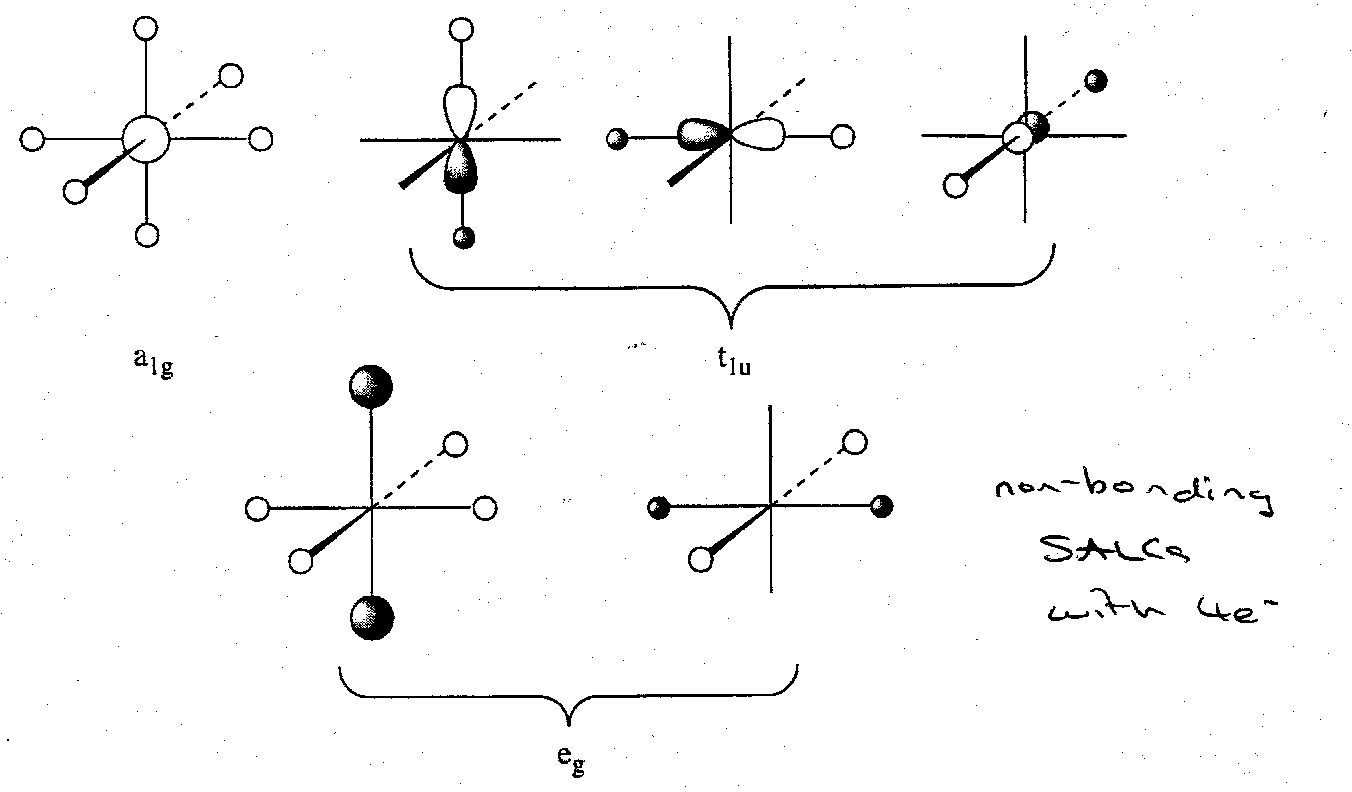
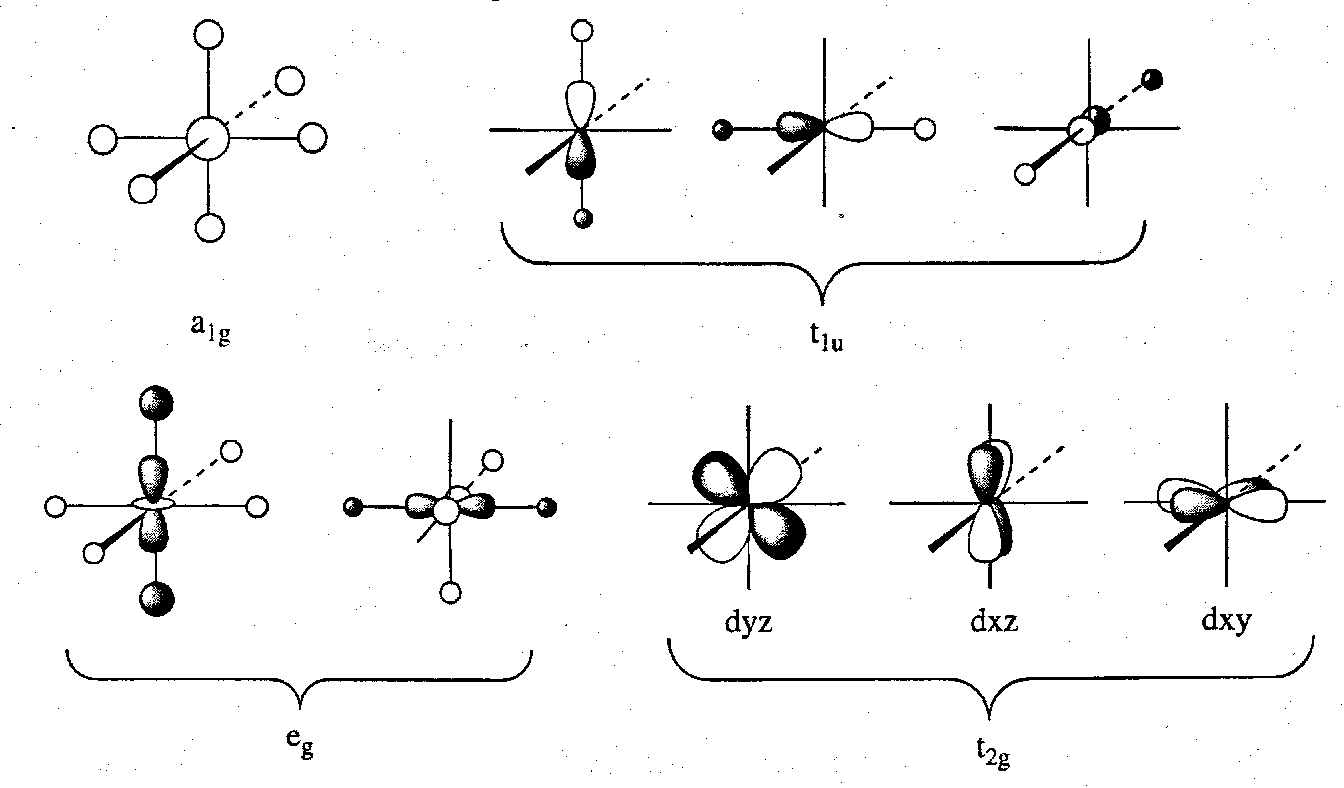
The general result for any AH6 σ-only octahedral complex with s, p and d AOs gives rise to 15 MOs, 2a1g + 2t1u + 2eg + t2g, and this is useful later on when considering transition metal complexes.

In the post-transition metal complexes, we need only consider two distinct cases – with or without nd orbital participation.

If we first consider the nd AO as being too high in energy to contribute to bonding, symmetry analysis predicts 4 bonding MOs, 4 antibonding MOs, 5 A atom based non-bonding and 2 H atom based non-bonding.

The 4 A-H bonding LCAOs are depicted thus:

The subsequent MO diagram is:

The 12 valence electrons occupy the six lowest energy MOs. 4 highly delocalised electron pairs are involved in forming six A-H bonds. This clearly parallels the linear H3- case. Just as in H3-, there is a build up of electron density on the peripheral atoms. This actually accounts for the lack of formation of compounds such as XeH2 and SH6.

The best stabilisation of a 12-electron AH6 system will arise when the terminal atoms are electronegativity ones, i.e. best able to stabilise the build up of negative charge. If the peripheral ligands are electropositive then the 1eg set will lie at high energy and the compound would be expected to undergo oxidation very easily (inherently unstable).

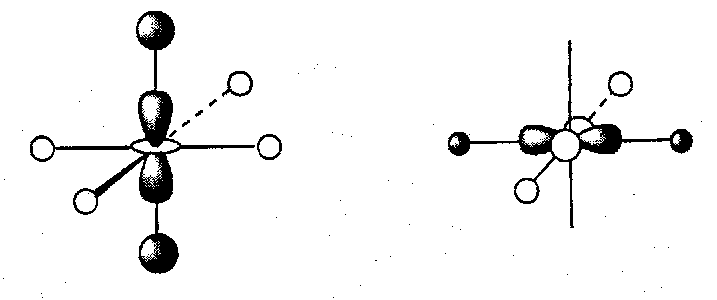
Considering now the effect of bringing the five nd orbitals into the bonding picture. The t2g set are unable to find a match with any of the H SALCs, but the eg set have the correct nodal properties and symmetry to interact with the previously non-bonding H eg SALCs. This can be depicted thus:

The effect of introducing d-orbitals into the A-H bonding can be illustrated:

It is apparent that the previously non-bonding 1eg set is stabilised. However, the extent to which d-orbital participation contributes to the bonding in post-transition metal compounds is still subject to investigation.

All things considered it is currently believed that the role of d-orbitals in such compounds is at most minimal; the bonding is best considered in terms of multi-centre bonding with d-orbitals making only a minor contribution.

Molecular Orbital Analysis of Transition Metal Complexes

This is particularly useful to consider over the Ligand Field Theory approach when looking at complexes such as Cr(CO)6 (zero oxidation state and neutral ligands), i.e. a more covalent bonding model is likely to be more accurate.

Octahedral Transition Metal Complexes: σ-bonding

This is typified by ligands such as NH3, H and CH3.

d-Orbital Overlaps –

This is small as they belong to the inner quantum shell and are not very radially extended. The overlap improves on going down a group as the d-orbitals acquire radial nodes and extend more into the interatomic region. Hence, we expect transition metal– ligand bond strengths to increase down a group. This contrasts with the situation for main group metal-ligand bond strengths which tend to decrease.

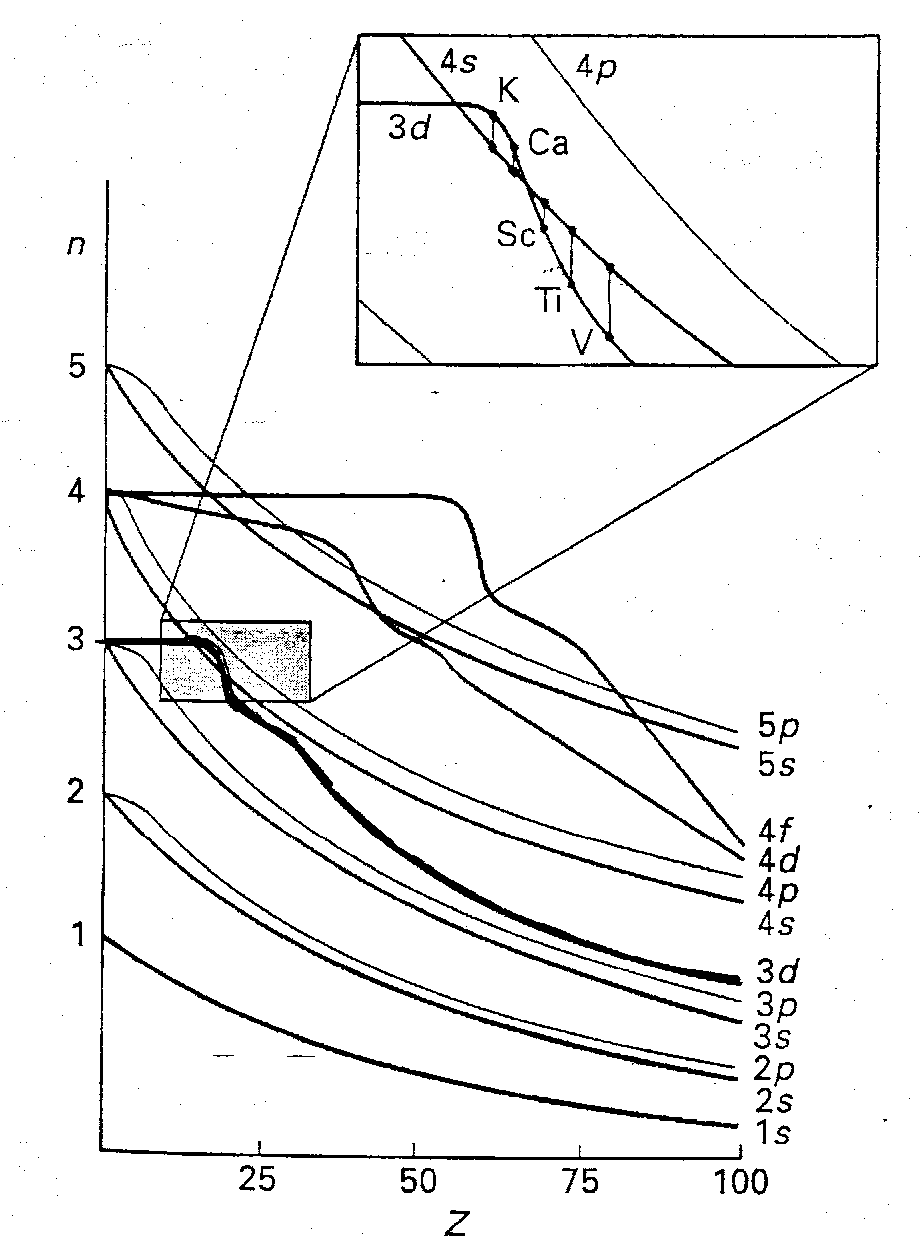
d-Orbital Energies –

For Transition Metals, the valence AOs are the (n+1)s, (n+1)p and nd. Of these three sets, the nd orbitals are the most stable of the valence orbitals in metal complexes (shown right).

The nd orbitals are stabilised on crossing the transition series, and after the end of the series are best considered as being core-like and playing no further direct role in metal-ligand bonding (as for SF6).

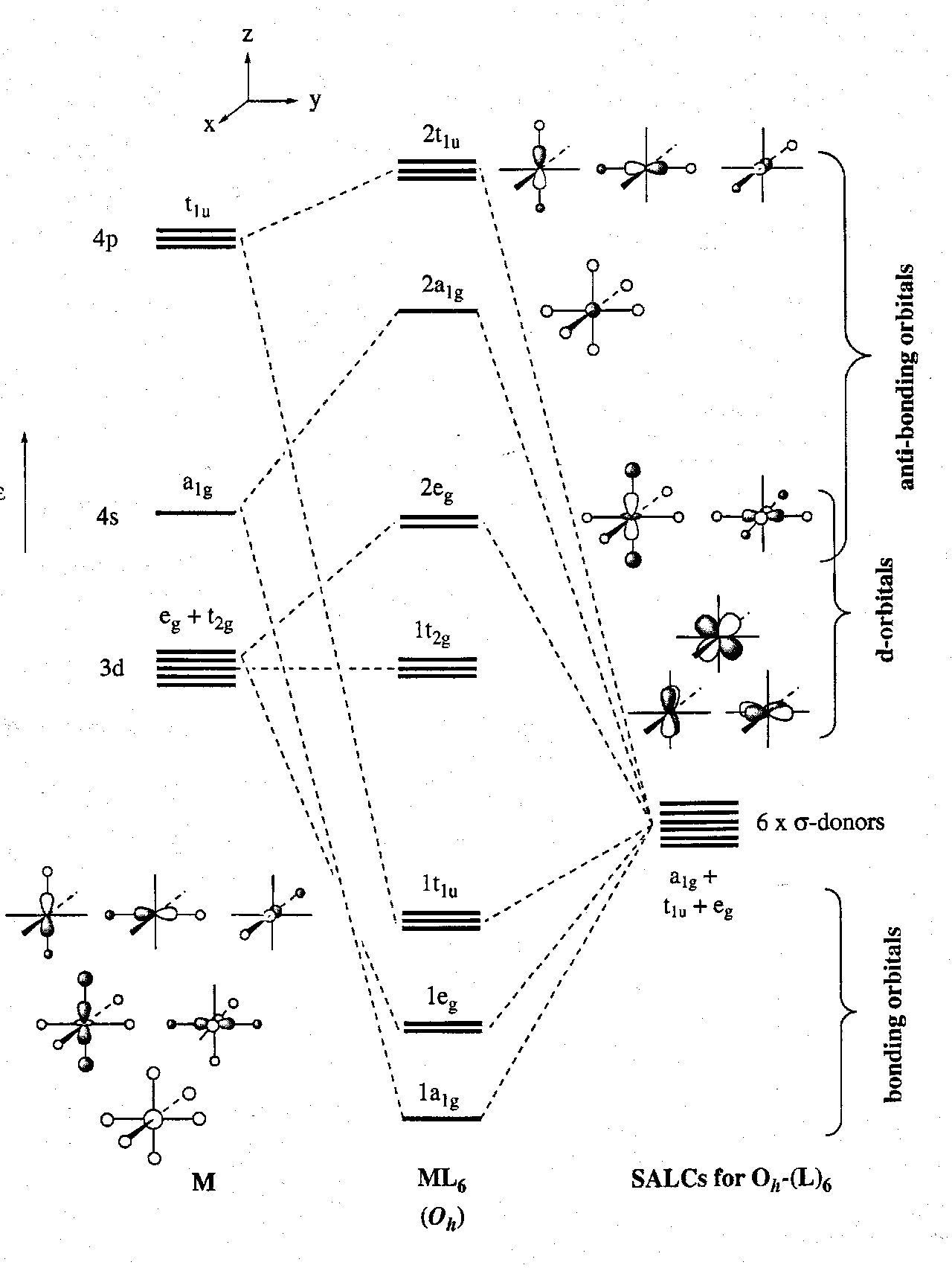
For a hypothetical ML6 complex with σ-only donor ligands (symmetry properties are the same as H 1s orbitals), we have already considered the symmetry analysis. We must remember to include the d orbitals this time, however.

The six M-L σ-bonding + the t2g non-bonding LCAOs are depicted:

The MO Diagram for a model first row octahedral metal features featuring only σ-interactions:

A number of important points follow from this scheme:

• The 1a1g, 1eg and 1t1u form a set of M-L σ-bonding orbitals. Because M is less electronegative than L they are more localised on the ligands than the metal. In other words, electrons in these MOs are ligand-based.
• The 2a1g, 2eg and 2t1u orbitals form a set of M-L σ-antibonding orbitals. They are localised on the metal. Populating these will obviously weaken the M-L bond.
• The 1t2g and 2eg σ-antibonding MOs have entirely or predominantly d orbital character. Any electrons in these are considered to be “d-electrons”.
• It is therefore clear from the MO diagram that any metal complex MLn can never have electrons in the s-orbitals despite any corresponding gas-phase atomic configurations. All metal-localised electrons in transition metal complexes are best considered as “d-electrons”, i.e. Cr(g) = 3d54s1 while Cr(0) in Cr(CO)6 is 3d6.

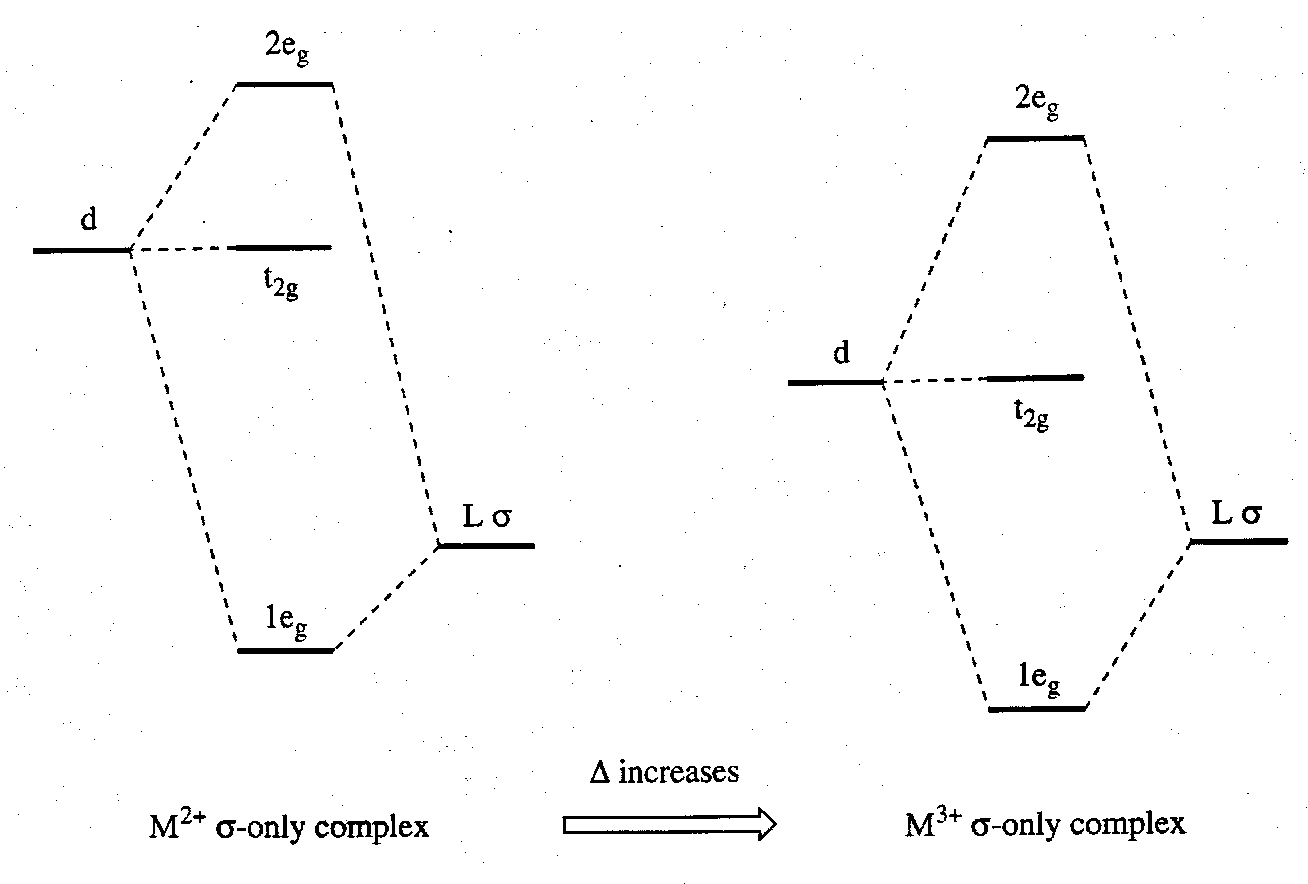
In the case of σ-only bonding ligands the 2eg to 1t2g separation depends on the strength of the M-L σ-interaction. This should:

• Increase on going down a group as M-L overlap increases.
• Increase with charge on the metal, as this will stabilise the d-orbitals and decrease the energy gap between metal and ligand orbitals.

MO filling in Octahedral Complexes

For an octahedral compound to be fully bonded we need 12 electrons to occupy the bonding orbitals. The t2g and eg are not necessarily filled.

Hund’s rules tell us that an atom or molecule achieves a lower energy if electrons are placed in separate degenerate orbitals with the same spin. This is because such a state keeps the electrons further apart, decreases electron-electron repulsion, and maximises exchange energy.

If the lowest energy available orbitals are close in energy, but not actually isoenergetic, it may still be advantageous to populate them separately with electrons of parallel spin rather than pairing electrons in the same, lower energy, orbital. This leads to the concept of low-spin and high-spin complexes.

High-spin and low-spin complexes: For octahedral complexes with between 4 and 7 d-electrons there are two alternative ways of filling the d-orbitals. The complex may either maximise the spin putting electrons into the upper eg orbitals, or fill the lower t2g orbitals pairing the electrons. The size of Δo relative to the pairing energy is critical in determining whether a complex is high or low spin.

Octahedral Transition Metal Complexes: π-interactions

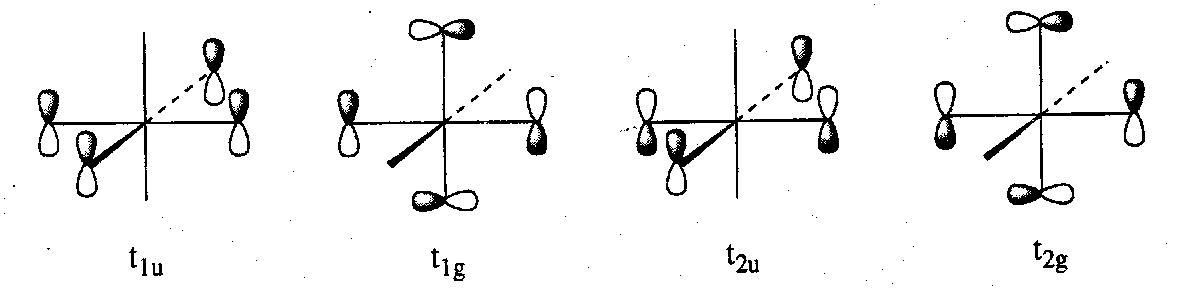
It is necessary for a complete picture to consider the π-orbitals that may be present on the ligand. It is only the t2g combination of π-orbitals on the ligands that has a productive symmetry match among the metal valence set. The possible SALCs of ligand π-donor orbitals are shown below:

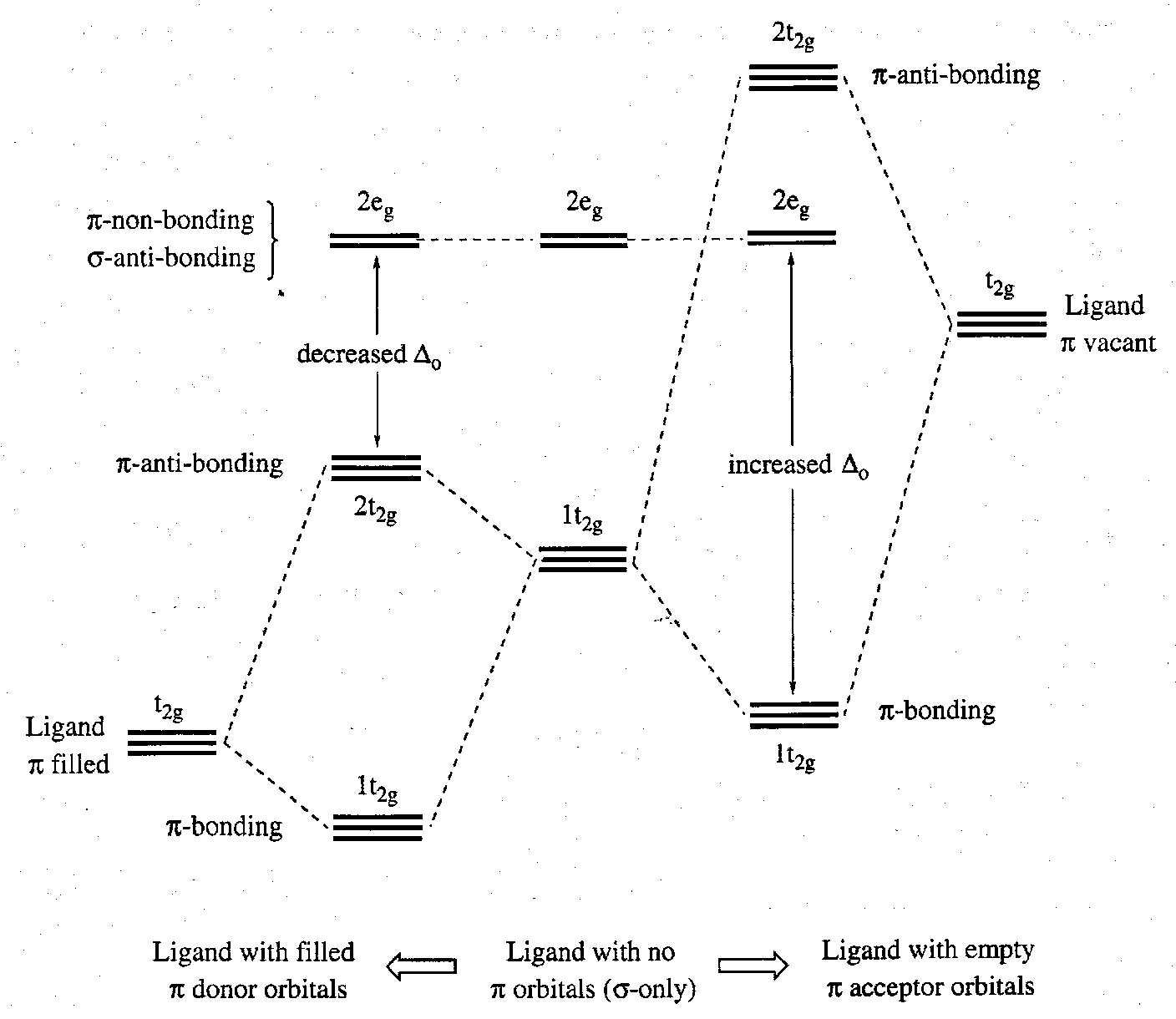
Ligands tend either to have low-lying π-orbitals that are occupied (e.g. F, Cl, NR2) or higher lying π-orbitals that are unoccupied (e.g. CO, CN-). The effect on the largely metal t2g orbitals will differ in the two cases. The nature and extent of the π-interaction is very important in determining the size of Δ.

• π-donor ligands destabilise the metal t2g d-orbitals. These metal-localised MOs become M-L π-antibonding. The magnitude of Δ decreases. A consequence of these effects is that π-donor ligands tend to stabilise high oxidation states (i.e. low d electron counts).
• π-acceptor ligands stabilise the metal t2g d orbitals these metal-localised MOs become M-L π-bonding. the magnitude of Δ increases. A consequence of these effects is that π-acceptor ligands tend to stabilise low oxidation states (i.e. higher d electron counts).

Factors that affect the magnitude of Δ

The size of Δ may be found empirically by analysis of the electronic spectra of transition metal complexes. It is found to depend principally on the following factors:

Nature of the Ligand –

Ligands are ordered according to the relative magnitude of Δ they produce. This order is known as the Spectrochemical series. For the more common ligands:

The Spectrochemical series is rationalised in terms of the σ / π donor/acceptor properties of the ligands. π donor/acceptors have already been discussed. σ-donor ability is rationalised by noting that the metal eg symmetry d orbitals are metal-ligand σ-antibonding. Ligands that are good σ-donors form complexes in which the σ-bonding 1eg MO is better stabilised. Consequently the metal-based 2egorbitals are more strongly antibonding and thus higher in energy.

Principal Quantum Number of the Metal –

The overlap between metal d orbitals and the ligand orbitals increases down a transition metal group. This results in an increase in Δ as the metal eg orbitals become more strongly antibonding.

The Charge on the Metal –

The t2g-eg splitting tends to increase with charge when M-L σ-interactions are the most important feature in the bonding. this is because the charge stabilises the metal orbitals and brings them closer in energy to the ligand orbitals.

However, a balance needs to be struck between any improved σ-interactions as the d orbitals are stabilised and any decreased π-bonding as the metal t2g orbitals move further away in energy from any ligand π-acceptor SALCs. For example, both Fe(CN)64- and Fe(CN)63- have the same value of Δ. This is because as the 3d orbitals get closer in energy to the σ-donor orbital they get further away from the π-accepting orbital of CN-.

Molecular Orbitals for 4-coordinate geometries, ML4 (Td and D4h)

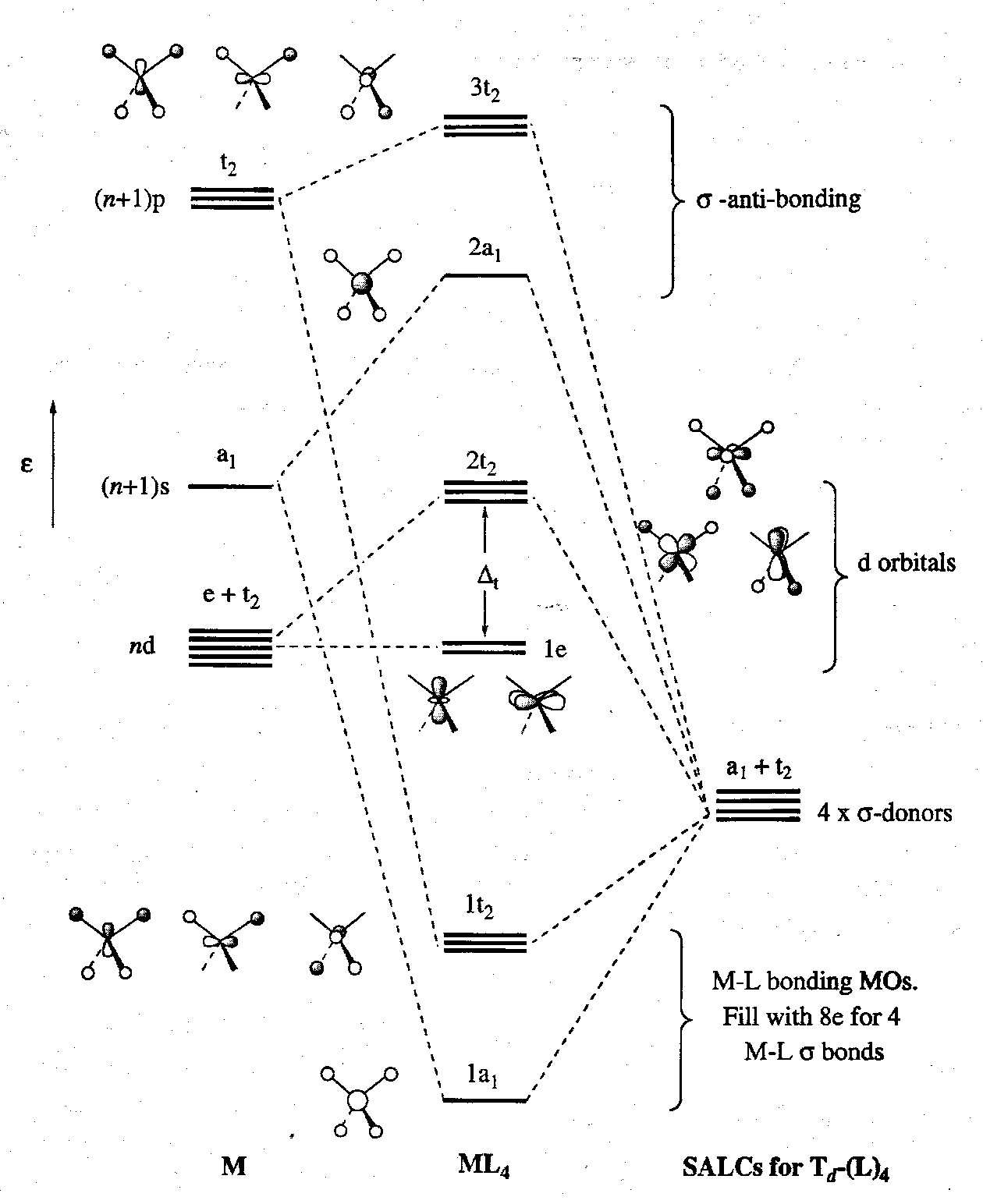
Tetrahedral ML4 Complexes

The MO Diagram is thus:

Notice that the 1e and 2t2 orbitals are analogous to the octahedral non-bonding d-orbital character t2g and eg orbitals. The separation between 1e and 2t2 is often referred to as Δt. The value is less than half that of Δo for the same ligand set. This can be attributed to the following:

• fewer ligands in an ML4 complex.
• Competition between the (n+1)p and nd metal AOs for the 4L t2 SALCs, thus helping to keep the d orbital localised 2t2 set relatively low in energy.
• The diminished metal-ligand σ-overlaps between the d orbital t2 AOs and the Td 4L SALCs in ML4 compared with those for the eg AOs and Oh 6H SALCs in ML6. This is a consequence of the relative spatial arrangements of the metal d AOs and ligand SALCs.

It has been established that Δt ≈ 4/9 Δo. A consequence of the small splitting is that virtually all Td complexes of the first row transition metals are high spin (Δt < spin pairing energy even for strong field ligands).

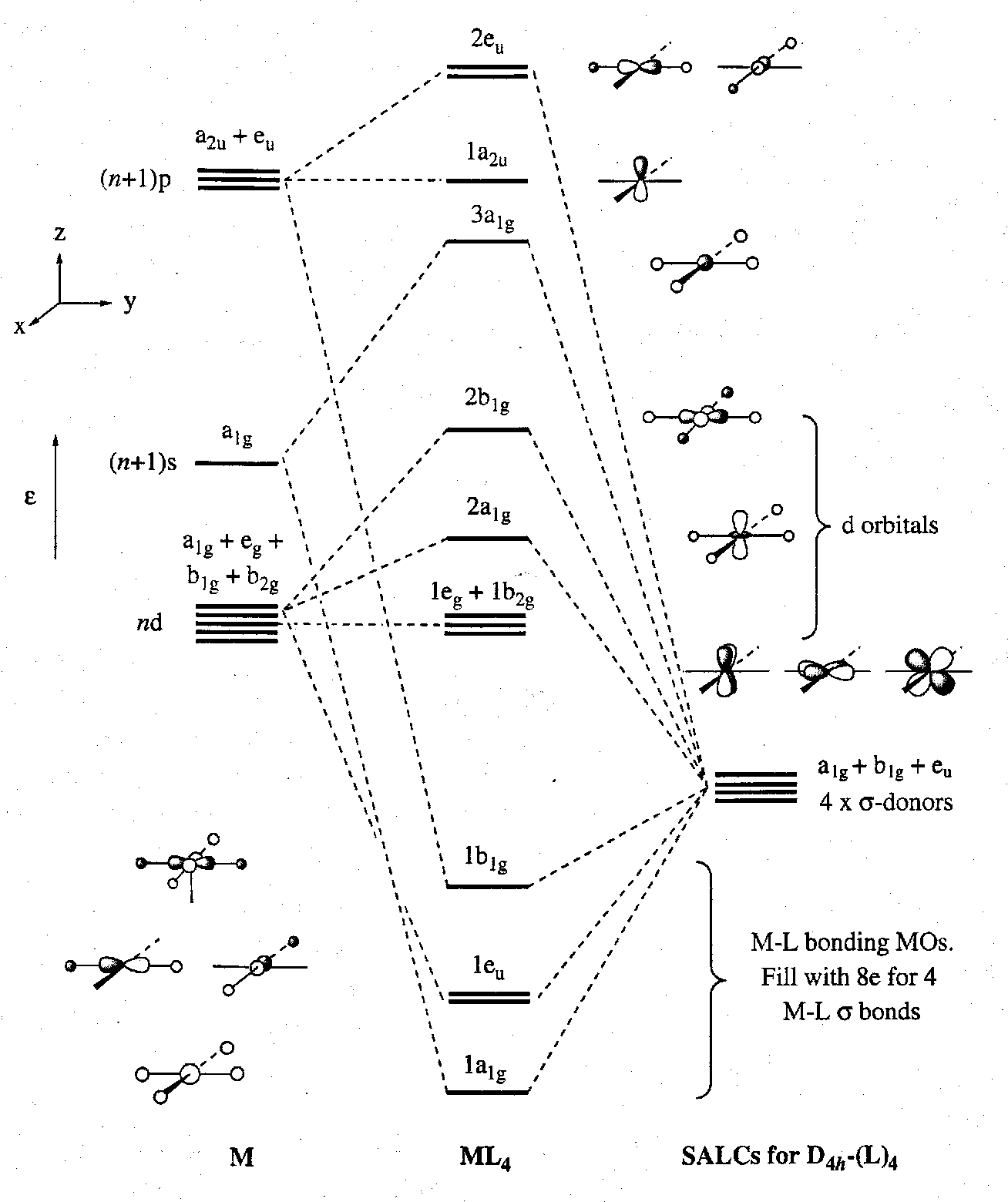
Square Planar ML4 Complexes

MO Diagram is thus:

We see from the MO diagram that:

• There are four strongly σ-bonding and strongly σ-antibonding levels. The former set accommodate the eight pairs of electrons required to form the four M-L σ-bonds. Another a1g symmetry MO is found at intermediate energy. This is because there are two AOs on the metal that can interact with the Ligand a1g SALC. As usual, it is the (n+1)s metal orbital that overlaps best with the ligand donors. Hence the only weakly antibonding “middle” level, namely 2a1, has predominantly ndz2 character.
• There are four strictly (by symmetry) σ-non-bonding MOs. The 1a2u lies relatively high in energy because it is pure (n+1)pz AO in character. The 1eg and 1b2g are mutually isoenergetic, but are not all degenerate by symmetry.
• The 1eg and 1b2g orbitals are equivalent to the triply degenerate t2g d orbital manifold in octahedral ML6 complexes, and can potentially engage in M-L π-bonding.