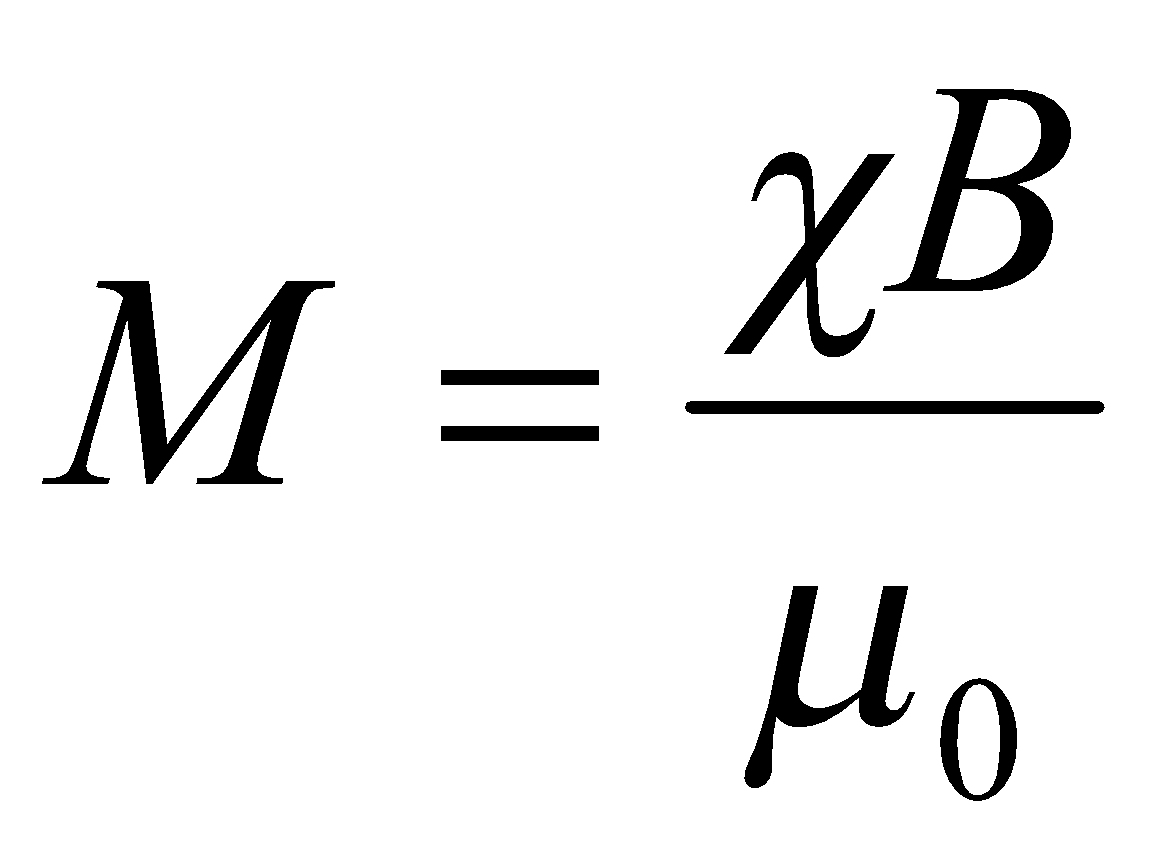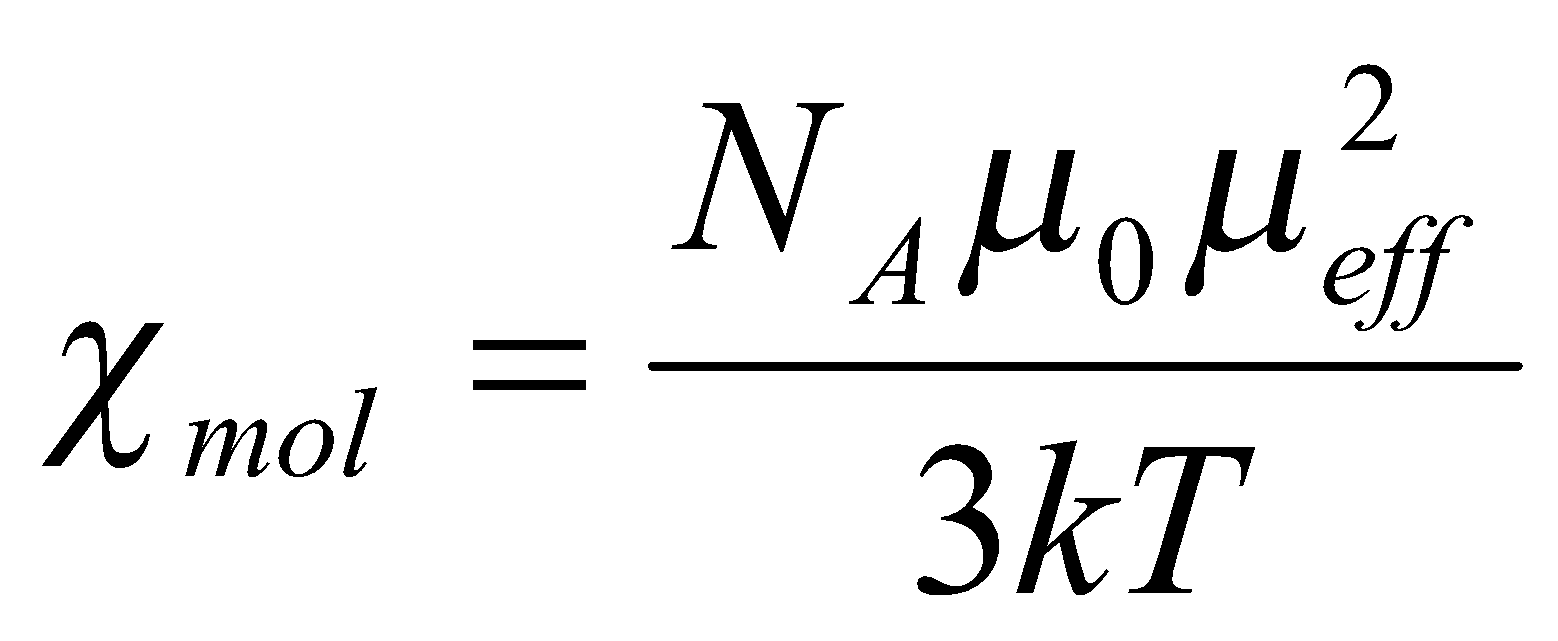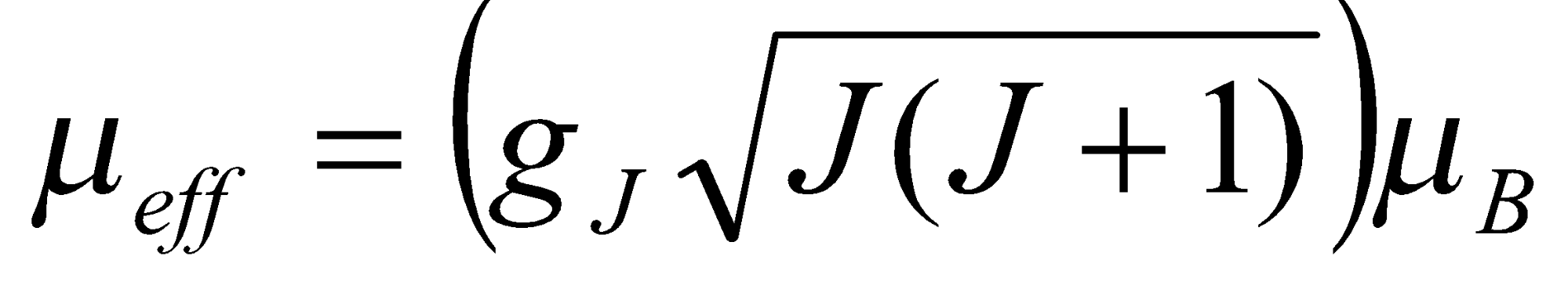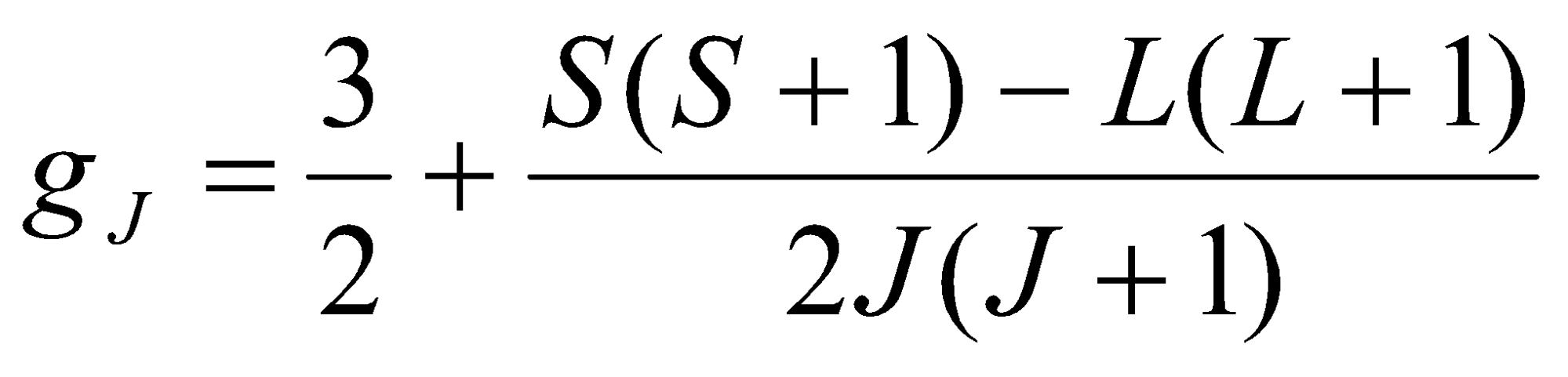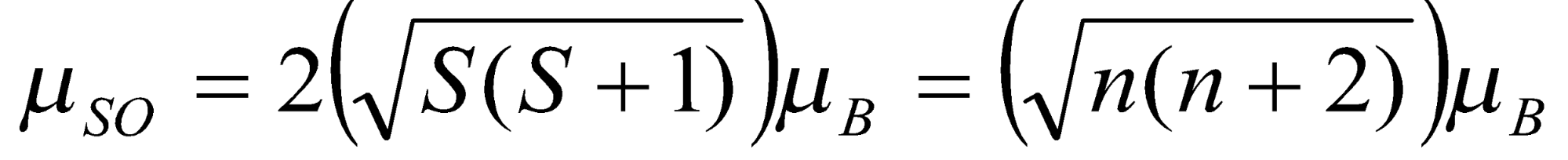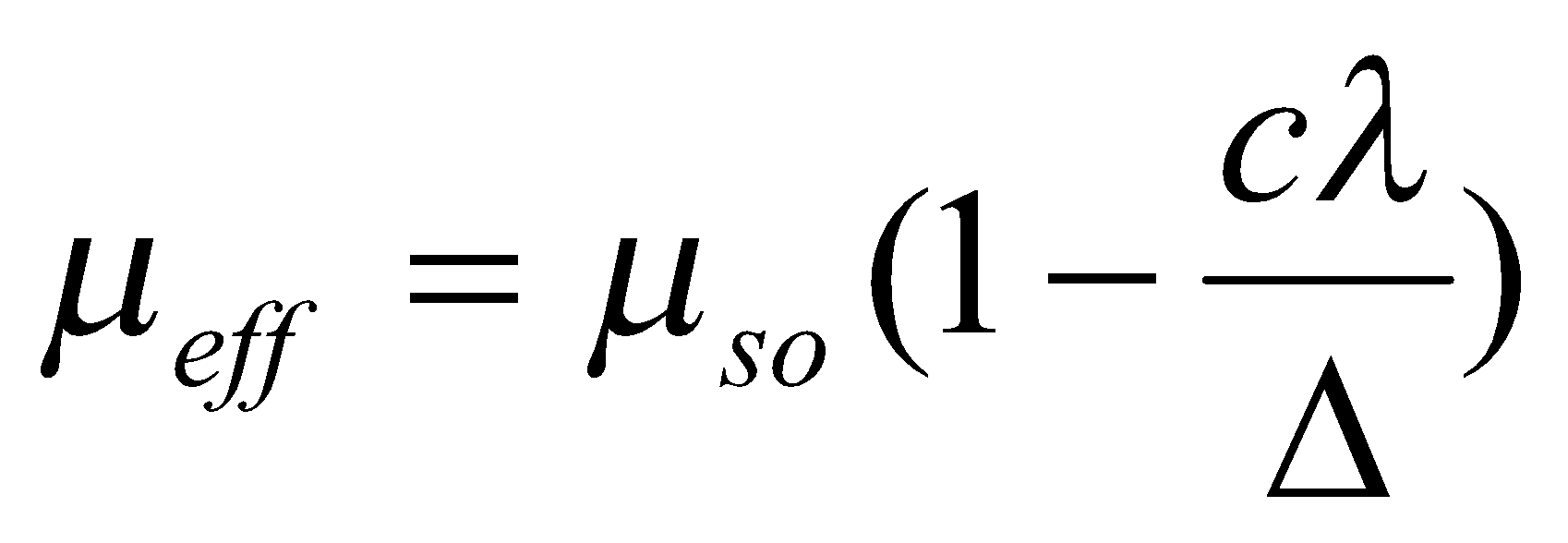Magnetism Notes

Magnetism generally occurs for all materials, and is a result of Lenz’ Law, which indicates that when a magnetic field is applied to a substance, it responds by opposing that field by creating an induced field due to its electrons. This phenomenon is known as diamagnetism.

Magnetic properties can be increased when unpaired electrons are present, where the material is instead attracted to an applied field as a consequence of spin and orbital angular momentum. This is called paramagnetism. It can also arise by “mixing in” of excited states to give a small effect (Temperature Independent Paramagnetism, TIP) and free electrons in a metallic solid also give a contribution (Pauli Paramagnetism).

The magnetization, M, and magnetic susceptibility, χ, of a substance is defined by:

.

There exists a further 3 types of magnetism, all of which are examples of cooperative magnetism.

Ferromagnetism:

The state where the spins on different metal centres are coupled into a parallel alignment that is sustained over thousands of atoms in a magnetic domain. The net magnetic moment increases (often greatly) as the individual spins augment each other. It generally occurs in materials containing unpaired electrons in d/f orbitals that can couple with similar orbitals on adjacent atoms. The key feature is that this interaction is strong enough to align spins but not to form covalent bonds (pairing of electrons).

Antiferromagnetism:

In this case, neighbouring spins are locked into an antiparallel alignment and this reduces the magnetic moment. It is often shown by paramagnets being cooled to a low temperature (and the magnetic moment then falls). It is usually brought about by an intervening ligand with paired spins causing polarization.

Ferrimagnetism:

This can be thought of as essentially a combination of the two above examples. There is a net magnetic ordering but the difference is that ions with different local moments are present. These ions order with opposite spins, as in antiferromagnetism, but because of the different magnitudes of spin moments do not cancel out completely and there is a net overall moment. As with antiferromagnetism, it is often caused by a polarising bridging ligand.

Curie Law

The paramagnetic susceptibility due to ions with magnetic moments often approximately obeys the Curie Law, χ=C/T, where T is the absolute temperature. There are several conditions under which this applies:

1. single degenerate ground state separated from all other states by energies much greater than kT.
2. the Zeeman splitting in the ground state is much less than kT.
3. the ions are magnetically dilute (do not interact significantly with each other) – i.e. not ferri-, ferro-, antiferro-magnetism effects.

The Curie Law can be written as:

Lanthanides

The lanthanides illustrate simple paramagnetic effects. They are paramagnetic because the f-electrons are often unpaired in their orbitals and also held tightly in by the nucleus and unavailable for bonding (essentially free ions). The degree of paramagnetism can be approximated quite accurately by the Lande formula which takes into account Spin-Orbit Coupling (using Russell-Saunders):

        with        

Transition Metals

The transition metal ions are also often paramagnetic. The difference here that needs to be considered is that the ligand field splittings give rise to a quenching of the orbital angular momentum present in free ions, and so a different approximation is used. It is called the spin-only formula:

, where n = 2S = number of unpaired electrons.

Deviations

The lanthanides experience deviations from the predicted results mainly due to two effects:

1. At low temperatures small ligand field splittings become significant, invalidating the approximation.
2. Sm3+ and Eu3+ have ground states with low moments and also low-lying excited states which are thermally accessible. When the occupation of these excited states with higher J-values are taken in to account, the approximation can be adjusted and the value obtained is accurate.

Deviations for the Transition Metals are normally due to either spin-orbit coupling occurring and/or incomplete quenching of orbital angular momentum. The Ground State configuration is often relevant in deciphering the deviations.

For example, for the A1 ground state there should be very little deviation (it is found to be the Ground State for d=0,5,10). This is a consequence of a perfectly symmetrical ground state configuration, and matches the spin-only prediction as a result.

For A2 and E ground states, there is the possibility of mixing of angular momentum between ground state and excited states. This should not depend on temperature. For A and E ground states, the following formula for a more accurate value for μ is often useful:

For T1 and T2 ground states there is likely to be incomplete quenching of the orbital angular momentum. This results in an additional orbital contribution to the magnetic moment, and spin-orbit splitting effects. The latter is temperature dependent, and Kotani Diagrams are often used to interpret this:

Another major deviation that can be seen using thermal data is spin crossover. This occurs where the ligands surrounding a transition metal give a Δ which is around the borderline between high and low spin states. Thus, at lower temperatures, low spin is favoured but when heated, the energy supplied allows the electrons to occupy higher energy unpaired states, giving a much higher magnetic moment.

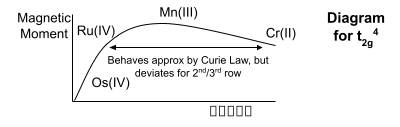
Also worthy of note is the possibility of metal-metal bonding (particularly for 2nd/3rd row Transition Metals). This quite simply occupies the unpaired electrons in the M-M bonds, so the magnetic moment is reduced.