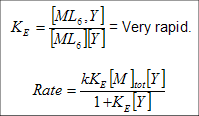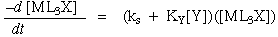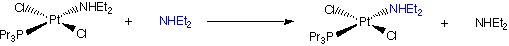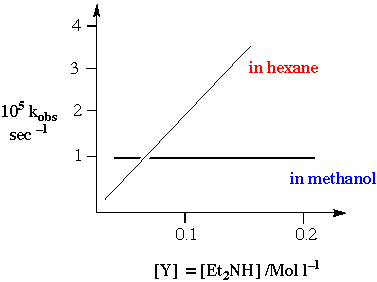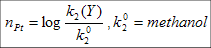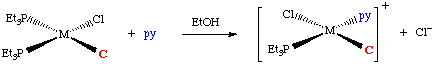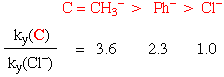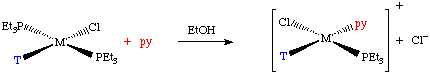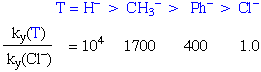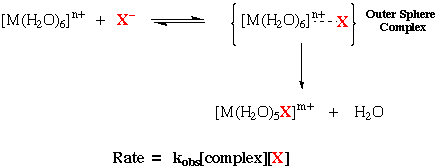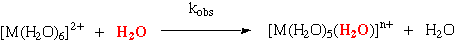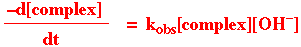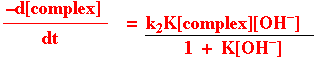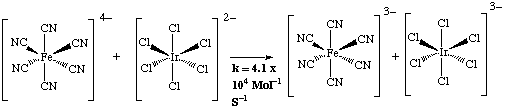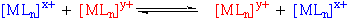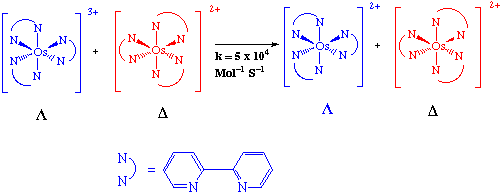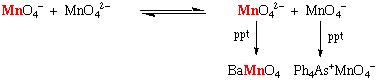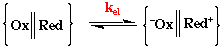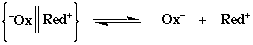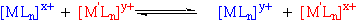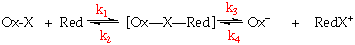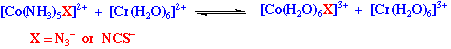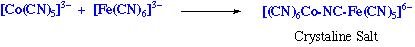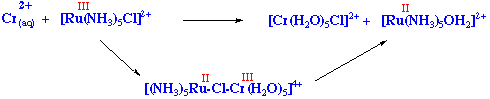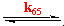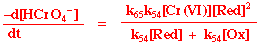Inorganic Reaction Mechanisms and Redox

Mechanisms

Dissociative (D) Mechanism

MLnX → MLn + X  → MLnY + X

Rate is independent of Y, and is determined by the breaking of the M-X bond (analogous to SN1).

Associative (A) Mechanism

MLnX + Y → MLnXY → MLnY + X

Common for Square Planar complexes.

Also, there is often a stereochemical change from the A mechanism, via an intermediate (analogous to SN2).

There is a third type of mechanism, distinguished by the fact that the intermediate cannot be isolated, and is thus some sort of amalgamation of the A and D mechanisms.

Interchange (I) Mechanism

MLnX + Y                MLnY + X

Y--MLn--X

This is common for 6-coordinate complexes.

It can have greater A or D mechanism characteristics, denoted Ia and Id.

Eigen-Wilkins Mechanism (for describing I kinetically) –

ML6 + Y ⇌ ML6Y → ML5Y + L

If KE[Y] << 1,

rate = kobs[M]tot[Y]

kobs = kKE.

If KE[Y] >> 1, i.e. Y is the solvent, kobs = k.

Factors Favouring A or D (or Ia or Id)

Sterics – Bulky ligands clearly will obstruct the nucleophile, so favouring the D mechanism over A.

Large Metal Ion favours A (easy attack by Y).

Good Leaving Group favours D.

Nucleophilicity highly favours A. I- is good for soft metals, F- good for hard metals.

Spectator ligands – no trans effect present for octahedral. However, strength of ligand matters. A good σ-donor increases e-density on the metal, so M-X breaks more easily. They may also stabilise low coordination number activated complex after the dissociation.

Associative Activation –

Shrinking as ligand binds leads to increased A character. Thus, increase in number of non-bonding d electrons increases the volume of activation, so more Dissociative. Low d-count implies Ia.

For large metals, a large ΔV is seen because they are more accessible. Also low non-bonding d count. Hence, tend towards Ia.

Substitution at Square Planar Metal Complexes

General Rate Law:

Factors Which Affect The Rate Of Substitution

1. Role of the Entering Group

2. The Role of The Leaving Group

3. The Nature of the Other Ligands in the Complex

4. Effect of the Metal Centre

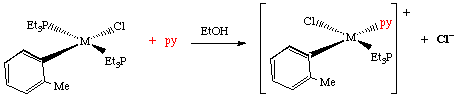
An illustration of the importance of solvent on the substitution pathways for square planar reaction centres.

1. Role of the Entering Group

• Rate is proportional to the nucleophilicity of entering group
• Element specific
• It is best to define the strength of Y by the term NUCLEOPHILICITY – the rate of attack on a complex by a given Lewis Base (relative to the rate of attack of a reference).

The nucleophilicity parameter is calculated as:

Reference reaction is:

Trans-[PtCl2(py)2] + Y → trans-[PtCl Y(py)2]+ + Cl-

Y best when CN-/CO, and worst when H2O/F-.

The opposite is true for X. A good nucleophile is a bad leaving group (relevant for the D mechanism).

• No correlation of nPt scale with other properties of the nucleophiles, such as basicity, redox potentials, or pH, e.g. strongly basic ligands such as OH- or OMe- do not react with Pt(II) substrates.
• For the reactivity series I- > Br- > Cl- the most important factor seems to be the polarisability or "softness" resulting from the existence in low lying excited states.
• PR3 > AsR3 > SbR3 >> NR3 
• Notable exceptions to this series are NO2-, SeCN-, which are "biphilic".
• "Biphilic" ligands exhibit different reactivities depending on the charge on the complex.

Biphilic Ligands:

• Biphilic properties originate from -acceptor properties from non-bonding electrons
• Availability of non-bonding electrons is dependent on ligand environment

2. The Role Of The Leaving Group

For the reaction:

[Pt(dien)X]+ + py →[Pt(dien)(py)]2+ + X-

in H2O at 25oC the sequence of lability is:

NO3 > H2O > Cl >Br > I > N3 > SCN > NO2 > CN

with a spread of over 106 in rate across series.

Leaving group does not affect the nucleophilic discrimination factors only the intrinsic reactivity.

The series tend to parallel the strength of the M-L bond.

3. The Nature of other Ligands in the Complex

The Trans Ligands

Definition:

The trans effect is best defined as the effect of a coordinated ligand upon the rate of substitution of ligands opposite to it.

For square planar complexes, this is a kinetic effect.

T is a spectator ligand trans to the Leaving Group. If T is a π-donor it will push electrons in to the metal, and weaken the M-X bond opposite it.

π-acceptors instead stabilise the transition state by reducing the electron density in antibonding orbitals.

For example, in the substitution reactions of Pt(II) square planar complexes, labilising effect is in the order:

H2O ~ OH- ~ NH3 ~ amines ~ Cl- < SCN- ~ I- < CH3- < Phosphines ~ H- < Olefins < CO ~ CN-

Note that the "labilising effect" is used to emphasise the fact that this is a kinetic phenomenon.

This labilisation may arise because of destabilisation (a thermodynamic term) of the ground state and/or a stabilisation of the transition state.

 

The trans influence is purely a thermodynamic phenomenon. That is, ligands can influence the ground state properties of groups to which they are trans. Such properties include:

(i) Metal-Ligand bond lengths

(ii) Vibration frequency or force constants

(iii) NMR coupling constants

 

The trans influence series based on structural data, has been given as:

R- ~ H- ≥ PR3 > CO ~ C=C ~ Cl- ~ NH3

The cis ligands

In cases where a relatively poor nucleophile act as the entering group

Note: Compare with the trans series below, it acts in the same way.

4. Effect of the Metal Centre

The order of reactivity of a series of isovalent ions is:

Ni(II) > Pd(II) >> Pt(II)

• This order of reactivity is the same order as the tendency to form 5-coordinate complexes.
• The more readily the formation of a 5-coordinate intermediate complex is, the greater the stabilisation of the transition state and so the greater the bimolecular rate enhancement.

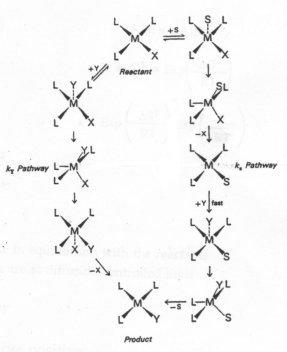
The Intimate Mechanism for Substitution at Square Planar Complexes

The associative pathways utilized in the substitution of one ligand for another at a square planar reaction centre:

The 1st order dependence of the rate of the reaction on:

• The concentration of the substrate
• The concentration entering reagent

Indicates that these complexes undergo substitution of ligands by a bimolecular mechanism.

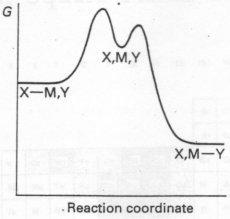
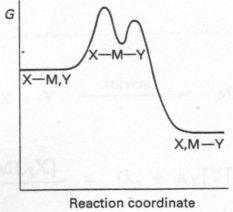
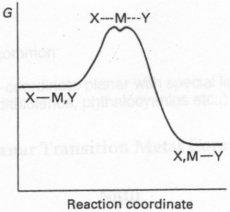
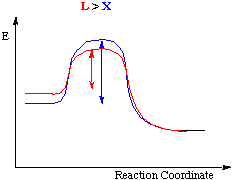
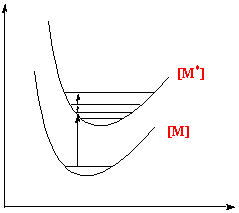
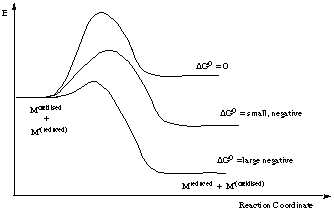
Some important points concerning the "intimate" mechanism

• Profile A applies when the energies of the reactants and products are almost equal, and in which the energies of the transition states are almost equal.
• Profile B is appropriate to a reaction for which the bond breaking is rate determining (D mechanism from the intermediate)
• Profile C depicts the situation when bond forming is rate determining, a situation in which the entering group (Y) lies higher in the trans effect series than the leaving group.

In a few cases the intermediate is reasonable stable and so lies at lower energy than the products.

General Substitution Reactions of Octahedral Complexes

Studies on octahedral complexes have largely been limited to two types of reaction:

Replacement of coordinated solvent (e.g. water). Perhaps the most thoroughly studied replacement reactions of this type is the formation of a complex ion from a hydrated metal ion in solution.

Anation: When the entering group is an ion the reaction is called anation.

Solvolysis. Since the majority of such reactions have been carried out in aqueous solution, hydrolysis is a more appropriate term. Hydrolysis reactions have been done under acidic or basic conditions.

General Comments

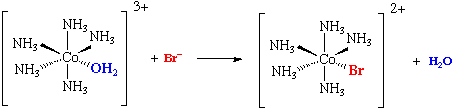
[M(H2O)6]n+ + X- → [M(H2O)5X](n-x)+ + H2O

Observations / Implications

• Rates quite similar to water exchange rates (H2O dissociation important factor)
• Rate increases with charge on anion ("Outer Sphere" Complex)
• Rate unaffected by nucleophilicity, basicity, etc... (A and Ia paths thus unlikely)
• Rate strongly dependent on M (suggests D or Id mechanism)
• Kinetics 2nd order (does not eliminate any mechanism)
• Intermediates not detected (very few cases, e.g. [Co(CN)5H2O]2-)
• V +ve, generally

All this generally suggests an Id mechanism.

General Scheme for Substitution Reactions

Rates of Water Exchange

The 1st Order rate constants for the substitution of inner sphere water in transition and non-transition metal complexes fall over 10-orders of magnitude.

General Comments

The rate constants of a given ion are approximately constant, no matter what the nature of the entering group. (evidence for dissociative activation)

The substitution rates divide the metal ions into 4-distinct groups:

Class 1	Very fast water exchange (k>108s-1), essentially diffusion controlled. These include the Group 1 and 2 ions (except Be2+ and Mg2+), Group 12 except Zn2+, and Cr2+ and Cu2+.
Class 2	Rate constants in the range 104-108s-1. This includes Mg2+, the Ln3+ cations, and most of the first row of transition metal divalent ions (except for V2+, and those in Class 1).
Class 3	Rate constants are in the range 1-104s-1. Examples are Be2+, Al3+, V2+ and some first row trivalent cations.
Class 4	Slow rates of water substitution down to <10-7s-1. Ions in this class are Cr3+, Co3+, and 2nd and 3rd row transition metal ions.

Factors which control the rate of H2O Substitution

For Class 1, ionic size, and ionic charge are clearly the important ones. As the ion becomes smaller the substitution rate slows. Reflecting importance of orbital overlap between metal ion and departing ligand. Group 2 and 12 show similar trend, (Be2+ is anomalous due to complex hydrolysis reactions).

For T.M. metals the correlation of rate with size is not obeyed, e.g. Cr2+, Ni2+, and Cu2+ have identical radii.

Mechanism – activation parameters have been determined for many water exchange reactions, and they support Id (Eigen-Wilkins) for ions of Groups 1,2,12,13 and the lanthanides (typically ΔSa and ΔVa > 0).

However, other data indicates that associative activation is also possible. This is particularly seen for early transition metal ions, but it changes to dissociative (Id) across the 1st row.

2nd/3rd row transition metal ions and more highly charged 1st row ions tend to follow the Ia mechanism.

The rationalisation for this is as follows:

• For ions following the Id mechanism, bond breaking is important in the rate limiting step and therefore one key factor must be the strength of the M-O interaction. We expect rate to increase as ionic radius increases and charge decreases. This is clearly the case for Groups 1,2 and 13, and most of the lanthanides. Hence Be2+ and Al3+ undergo slow water substitution.
• For transition metals the correlation between rate and size is not always obeyed, e.g. Cr2+, Ni2+ and Cu2+ have the same ionic radii. Octahedral Cr2+ (HS d4) and Cu2+ (d9) are susceptible to Jahn-Teller distortions which lengthen two of the M-O bonds, which will facilitate substitution by a dissociative mechanism (breaking a weaker bond).
• Group 2 vs. Group 13: Ca2+/Zn2+ and Sr2+/Cd2+ are as expected. Hg2+ faster than expected. Perhaps due to 2-short/four long Hg-OH2 bonds due to sdz2 hybridisation for d10.
• Ligand field stabilisation energies affect the rate for transitions metals. Essentially ions which have large LFSE’s will be less labile for both associative and dissociative activation. Hence d3 (e.g. Cr3+), d8 (Ni2+) and low spin d4, d5 and d6 are expected to be inert, while d0, d10, d1 and d2 can be expected to be much more labile, and the rate should also follow the order Mn2+ > Fe2+ > Co2+. Cr2+ and Cu2+, Jahn-Teller effect. Trivalent ions should have slower rates, as should second and third row ions.
• Al3+ is smaller than Cr3+ but the rate for Cr3+ is 3 orders of magnitude lower – effect of covalence and d electron configuration.

The many factors considered when assessing different rates are summarised below:

Charge – higher charge lowers the energy of d-orbitals, making them closer in energy to ligand orbitals. This leads to a better overlap, and a stronger bond (assuming they do not hydrolyse the water ligand).

Generally, as ΔHa decreases, k will increase (common sense!). Similarly, increased ionic radius leads to increased rate (bigger target!).

An entropy change greater than 0 indicates a Dissociative-like mechanism (more disorder in the transition state). Smaller radius also favours the D mechanism (harder to attack by nucleophile of A mechanism).

CFSE – lower is better, since reaction involves loss of stabilising CFSE influence.

Considering now the change in electron configurations and orbital splittings during the reaction:

Factors to consider here:

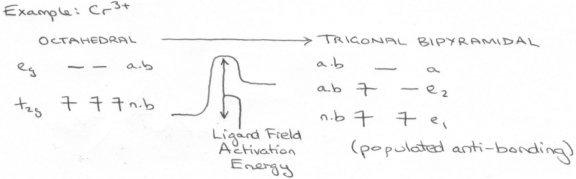
• d3 is inert, since to rearrange electrons, one must be promoted to an eg orbital (antibonding – expends energy). Thus ΔHa will be high.
• CFSE = 6/5Δo . This is at a maximum, and this energy is lost on change of configuration, which is a loss of stabilisation.
• Cr3+ is small and charged, so the Cr-O bond is likely to be strong. One of these bonds is lost on reaction.
• Mechanism requires population of an antibonding orbital in the intermediate stage – this is energetically unfavourable.

All of these lead to a high Ligand Field Activation Energy, and thus it can be seen why Cr3+ is very inert to substitution.

For less charged metals, and for metals with lower CFSE, the exchange will occur more rapidly.

Moving down a Group, the 4d and 5d orbitals are lower in energy, and make a closer energy match with better overlap to the ligands. This leads to a stronger bond, and so a higher ΔHa. Similarly, down the Group the orbital splitting is larger for 2nd/3rd row, which leads to a larger LFAE (bigger energy gap for promotion of any electrons into antibonding).

Another factor to consider is an increased Volume of Activation. This is a factor when there are more d electrons (e.g. in Ni2+), and leads to a greater entropy change, and drives the Dissociative mechanism of the reaction.

Predominant factor is electron configuration requirements, however.

Orbital Occupation Effects on Substitution Reactions of Octahedral Complexes

The basic assumption is that there is a significant contribution to the activation energy in a substitution reaction is the change in d-orbital energy on going from the ground state of the complex to the transition state. Any loss in energy would contribute to the activation (and slow the rate). Using this approach the [M(H2O)6]2+ ions show the following relative rates:

V2+ << Cr2+ >Mn2+ > Fe2+ > Co2+ > Ni2+ < Cu2+ > Zn2+

General Comments

Series is generally in good agreement with experimental data.

The d3 ions are predicted to be substitutionally inert.

Except for Ni2+(d8), the high spin d4-d10 M2+ ions are predicted to be labile by either C4v or D3h transition state pathways.

Some deviation that need further explanation: Cr2+(d4),and Cu2+(d9) complexes are especially labile. This is due as mentioned earlier to the Jahn-Teller effect.

Mn2+, Fe2+, and Co2+ are predicted to have equal labilities, but we observe experimentally that substitution rates decrease across the series. This is due to the increase in Zeff across the series and increase in E(M-L).

Stereochemistry of Substitution of Octahedral Complexes

General Points about Stereochemistry

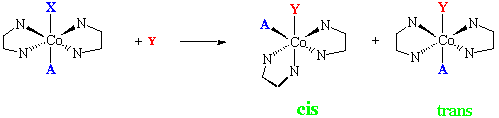
1. In general, trans-[Co(en)2ACl]2+ undergo stereochemical change on hydrolysis, whereas cis-[Co(en)2ACl]2+ react with retention of original chirality.
2. cis isomer generally react faster than trans isomers
3. Ligands A, that lead to stereochemical change in the trans series are those with p orbitals
4. If the reaction proceeds through a square pyramidal intermediate, retention of configuration will be observed.
5. Proceeding through a trigonal bipyramid, has 75% chance of leading to stereochemical change.

Points 3 and 5 above:

Stereochemistry of Substitution of Octahedral Complexes

Compound	D or Id Mechanism
	Tetragonal or Square Pyramid Intermediate			Trigonal Bipyramid Intermediate
	cis product	trans product		cis product	trans product
trans-ML4AXn+	0	100		66.6	33.3
cis-ML4AXn+	100	0		83.3	16.6
trans-M(L-L)2AXn+	0	100		66.6	33.3
cis-M(L-L)2AXn+	100	0		= 58.3 = 25.0	16.7

Hydrolysis under Acid and Alkaline Conditions

The hydrolysis reaction:

[ML5X]n+ + H2O → [ML5(OH2)]m+ + Xa-

This is often called aquation. The rate law for such a reaction is commonly of the form:

Rate = kA [ML5X] + kB[ML5X][-OH]

Water as the entering ligand (55.5M) does not appear in the rate law. This reaction has been studied extensively for Co3+ complexes. The second term occurs when there are ionisable protons in the complex. In general, kB (for base hydrolysis) is about 104 times kA (for acid hydrolysis).

Acid Hydrolysis –

Data for Co3+ complexes indicate an Id mechanism very close to the D limit.

• For [Co(NH3)5X]n+ the rates correlate well with the stability of the complexes, indicating that Co-X bond breaking in important in the rate limiting step.
• For a series of [Co(NH3)5(RCO2)]n+ complexes there was a correlation with the basicity of the carboxylate.
• For a series of substituted bidentate amines, the rate increases with increasing bulk of substituents on the chelating ligand (e.g. Me2en faster than en), indicating a dissociative mechanism.
• ΔV for X=Cl was close to the molar volume of water, indicating an Id mechanism close to the D limit.

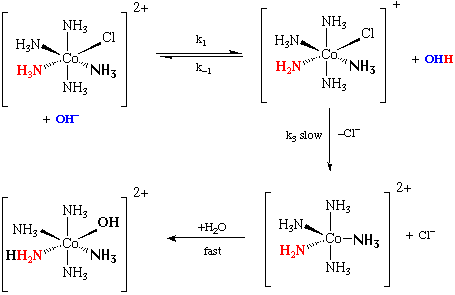
Base Hydrolysis –

As mentioned earlier the rates of substitution of octahedral complexes are not sensitive to the nature of the entering group-with one exception. In basic media Co(III) complexes having ligands of the type NH3, RNH2, R2NH are sensitive to the nature of the entering group.

The base catalysed reactions are generally much more rapid than anation or hydrolyses in acid solution.

The agreed mechanism, involves the removal of a proton from the amine ligand. This step is generally very fast, (105 faster), and represents rapid pre-equilibrium to the rate determining loss of leaving group.

The second order rate law for base hydrolysis of complexes with ionisable protons on the ligands does not arise from direct attack of –OH on the complex in an A mechanism. The reaction is generally accepted to occur via the conjugate base of the complex like so:

If, however, K is quite small (it is in the range 0.01-0.2 for Pt(IV) complexes) so that K[OH] << 1,, the rate law would reduce to that experimental observed.

• The rate of H/D exchange for the coordinated ammonia is 105 times faster than the hydrolysis reaction, consistent with the rapid pre-equilibrium between the complex and its conjugate base.
• The rate in the presence of the HOO- ion, which is a weaker base but stronger nucleophile than –OH, is slower.
• The acidity of coordinated ammonia is low, so the equilibrium concentration of the conjugate base is low, and the actual rate acceleration by the amide group is > 106.
• The proposed trigonal bipyramidal structure of the conjugate could result in stereochemical change.

Another factor which should be considered here, as well as those above for Water Exchange, is vacancy in the non-bonding orbitals. This is because the amide created in the base hydrolysis above is now a very strong π-donor, and the electrons it donates must enter low energy non-bonding orbitals in order to increase the rate. In fact, if the t2g is full, the rate will decrease due to the destabilising influence. This influence is worse when large splittings are involved, e.g. from strong field ligands or 4d/5d orbitals.

Electron Transfer Reactions

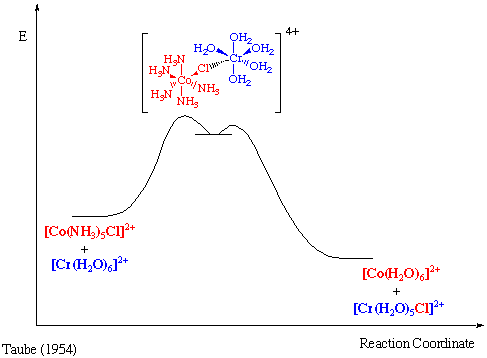
Electron transfer reactions may occur by two mechanisms: outer or inner sphere. In principle outer sphere mechanism involves electron transfer from reductant to oxidant with the coordination shells or spheres of each staying intact. That is one reactant becomes involved in the outer or second coordination sphere of the other reactant and an electron flows from the reductant to oxidant. Such a mechanism is established when rapid electron transfer occurs between two substitution-inert complexes.

An inner sphere mechanism is one in which the reactant and oxidant share a ligand in their inner or primary coordination spheres the electron being transferred across a bridging group.

Outer Sphere Electron-Transfer

Electron-transfer will lead to change in the total optical rotation, thus if equal concentrations of reagents are used:

Rate of Racemisation ≡ Rate of Electron Transfer

Studied by :

• Isotopic labelling with 54Mn
• 17O NMR studies

Mechanism

Electron transfer from the reductant to the oxidant, with the coordination shells or spheres of each staying intact. (One reactant becomes involved with outer sphere or second coordination sphere of the other reactant).

Such reactions are observed in electron-transfer reactions of substitutionally inert complexes.

Elementary Steps in the Outer Sphere Mechanism

Formation of a precursor (cage) complex

Chemical activation of the precursor,

electron transfer and relaxation of the successor complex

Dissociation to the separated products

kobs = KAkel

Step 1. Formation of the Precursor Complex

This step is always considered to be fast, the rate is generally determined by kel.

Step 2. Chemical Activation and Electron Transfer

Important factors are:

• Solvent reorganisation
• Electronic structure
• M-L reorganisation small

Franck-Condon Factors

Electron-transfer processes must satisfy the Frank-Condon restrictions, i.e. the act of electron transfer is much shorter than atomic motion. The consequences are that no angular momentum can be transferred to or from the transition state during electron transfer, there is also restrictions in changes in spin.

For example:

Has an outer sphere electron transfer rate of 1.1 M-1 sec-1, simply requires the transfer of electron from eg orbital of one Co to the other.

The reaction:

Is very slow k = 10-9 M-1 sec-1 requires a change of spin multiplicity as well.

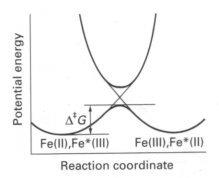
In addition the oxidant and reductant must structurally reorganise themselves before electron transfer so that the energies of their transition states are equal. For example:

If electron transfer took place at their equilibrium positions, then we would have compressed Fe(II) ion and a stretched Fe(III) ion. These are in vibrationally excited states and would release energy, contravening thermodynamics. Thus the reagents must match their energies before electron transfer can occur.

Generalised Rules for Chemical Activation

The factors mentioned above can be combined with basic MO theory to give a basis for predicting trends in electron transfer rates using electron structure arguments.

You could expect more facile electron transfer when both donor and acceptor MO's are * type.

Reasons are:

Changing M-L distance is usually less for a change in d* than d* orbital

Donor-acceptor overlap is better for * * transfer than * * transfer, since * orbitals point to faces of Oh rather than the corners (*)

How do you Spot an Electron Transfer Reaction ?

• Is it a Redox Reaction ?
• Are the Complexes Substitutionally Inert ?
• Do the Complexes contain Potentially Bridging Ligands ?
• Which Electrons are Being Transferred ?

* * (good especially for -acceptor ligands)

* *

Cross Reactions and the Marcus Equation

In general the rates of outer sphere electron transfers involving a change in free energy is given by the Marcus Equation:

k12 = (k1k2K12f)1/2

where K12 is the equilibrium constant for the cross reaction

k1, and k2 are the rate constants for the self exchange reactions

The parameter f is usually close to 1.

The barrier to electron transfer consists of two parts, the "intrinsic" contribution and the thermodynamic part (G12°).

The free energy of activation for electron transfer (G12 ) is given by:

Summary

Simple electron transfer. No sharing of ligands.

Occurs when redox is faster than ligand substitution. The key to the mechanism is the matching of the energies of the reactants.

To Enhance Outer-Sphere Electron Transfer Rates

• Minimal solvent reorganisation (large ligands)
• Small changes in M-L bond lengths (* -> *)
• Good orbital overlap (-> *, -acceptor ligands)

Ideally, the electron transfer should be between the same energies of reactants, so that electrons do not have to move (Frank-Condon Principle).

This means BOND LENGTHS adjust to match (ΔGin). There is also a solvent rearrangement factor, ΔGout.

An example:

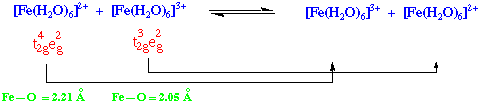
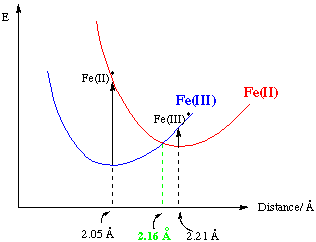
Fe(OH2)62+ + Fe(OH2)63+.

Fe(II) shortens, Fe(III) lengthens – minimises energy.

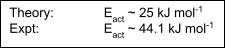
A high ΔHa indicates sharp potential curves as bonds distort, therefore a large ΔGa.

The degree of bond lengthening is governed by several factors.

Nature of Metal Centre – the larger 4d / 5d orbitals allow for greater bond length adjustments due to reduced e-e repulsions and larger orbital splittings.

Electron Configuration is often an important factor, since placing electrons into antibonding orbitals during oxidation increases bond lengths greatly. Also change from low to high spin expends energy. Both of these increase ΔGin.

Large metals (2nd / 3rd row) tend to be low spin, so do not vary bond lengths as significantly. This is because the low spin configuration means that antibonding orbitals are not occupied, and these would reduce bond lengths far more than non-bonding orbitals would.

Nature of Ligand – also an important factor. For example, the pyridine ligand, possessing a π-delocalised MO, can extend this over the metal t2g orbitals, which greatly decreases the reorganisation energy, so there is a faster transfer.

Strong field ligands may also split the crystal field of the metal greatly, making them adopt a low spin configuration. This reduces Δr as mentioned above.

Inner Sphere Electron Transfer

Reduction of hexaamminecobalt(3+) by hexaaquochromium(2+) occurs slowly (k = 10-3 M-1sec-1) by an outer sphere mechanism.

However, if one ammonia ligand on Co(III) is substituted by Cl-, reaction now occurs with a substantially greater rate (k = 6 x 105 M-1 sec-1).

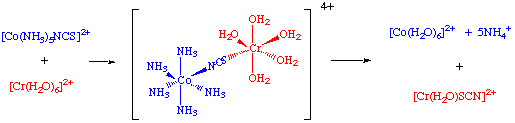
The reductant and the oxidant share a ligand in their primary coordination sphere, the electron being transferred across a bridging group.

Prerequisites for Inner Sphere Mechanism

One reactant (usually the oxidant) possess at least one ligand capable of binding simultaneously to two metal ions.

The other reactant is substitutionally labile; i.e. one ligand must be replaced by the bridging ligand.

Examples

Ligand transfer is not a requirement for inner sphere mechanism.

The Elementary Steps and Rate Expression for the Inner Sphere Mechanism

Ox-X + Red(H2O) Ox--X--Red + H=O

Formation of a precursor complex

Ox--X--Red -Ox--X--Red+

Activation of the precursor, and electron transfer

-Ox--X--Red+ + H2O Ox(H2O)- + RedX+

Dissociation to the separated products

The overall reaction can be given by:

k1 is rate limiting, formation of the precursor complex (usually substitution of the bridging ligand for H2O on the Red complex).

k3 is rate determining, electron transfer within the complex, or fission of the successor complex.

Both extremes give 2nd order kinetics

Important Factors which Affect the Rate of Inner Sphere Reactions

1. Formation of the Precursor Complex

This step is closely related to the rates of substitution in Octahedral Complexes.

• Octahedral d3 are relatively inert
• High spin d4 and d5 are labile

Thus the rates of electron transfer involving [V(H2O)6]2+ (d3) are comparable to the rate of water substitution.

2. Electronic Structure of Oxidant and Reductant

Many electron transfer reactions are greatly enhanced when they proceed via an inner sphere mechanism.

This can be explained by consideration of the symmetries of the reductant orbital from which the electron is lost and the oxidant orbital into which the electron moves.

EXAMPLE

The *→* electron transfer is the most accelerated, and is the route that requires most chemical activation, i.e. bond rearrangement in the transition state. These requirements seem to be largely over come by forming 3-centre bonds in the transition state.

 

3. Nature of the Bridging Ligand

Inner sphere electron transfer reactions are very sensitive to the nature of the bridging ligand.

The bridging group has two roles:

1. To bring the metal centres together (Thermodynamic contribution), important factor here is the stability of the intermediate, and M-L bond strengths.

2. The kinetic contribution is the transfer the electron, important factor is the matching of the donor and acceptor MO's.

Bridging ligands can be organic or inorganic.

However the major difficulty is deciding whether the e-transfer is either outer or inner sphere. A useful test has been developed, consider the reaction;

The azide ion can better form an intermediate, than thiocyanate.

Studies of inner sphere reactions involving organic bridging ligands, show that reduction rates can be controlled by steric effects, electronic structure of the bridge, the point on attack on the bridge, and its reducibility.

 

4. Fission of the Successor Complex

Occasionally, the rate determining step can be the fission of the binuclear complex, after e-transfer has occurred. For example

The reason of the stability of the binuclear complex in this case is that both Cr(III) (d3) and Ru(II) (d6) are substitutionally inert.

Differentiation between Outer Sphere vs. Inner Sphere Electron Transfer

1. Outer sphere mechanism is open to all redox active systems, while inner sphere mechanism requires substitutionally labile reactants and products.
2. Evidence from ligand transfer, labelling, etc..
3. V 
4. Marcus Relationship (outer sphere reactions)
5. N3- vs. NCS- ratio (Outer Sphere ) ~ 1

ratio (Inner Sphere) >> 1

 

Relative Rates of Reduction of N3- and NCS- Complexes

Oxidant	Reductant	k(N3-)/k(NCS-)	Reaction Type
[Co(NH3)5X]2+	Cr2+	104	inner sphere
[Co(NH3)5X]2+	V2+	27	not determined
[Co(NH3)5X]2+	Fe2+	>3 x 103	inner sphere
[Co(NH3)5X]2+	Cr(bipy)32+	4	outer sphere
[Co(H2O)5X]2+	Cr2+	4 x 104	inner sphere

Two Electron Transfer Reactions

Many p-Block and transition metals has stable oxidation states separated by two, and do not usually form stable in complexes with odd numbers of electrons;

e.g

Sn(II)/Sn(IV); Tl(I)/Tl(III); P(III)/P(V); Pt(II)/Pt(IV)

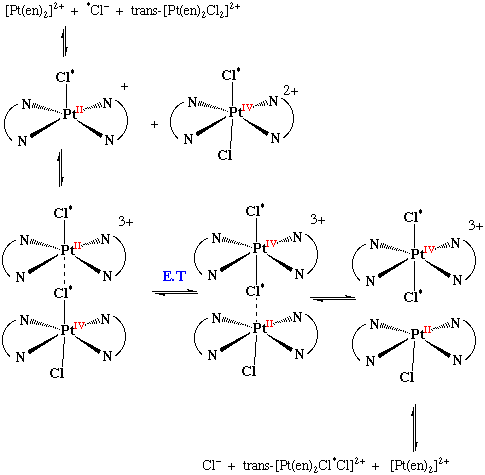
One of the best understood two-electron transfer reaction, in T.M. chemistry is the Pt(II)-catalysed exchange of free Cl- for chloride bound to Pt(IV).

[Pt(en)2]2+

trans-[Pt(en)2Cl2]2+ + *Cl- trans-[Pt(en)2*ClCl]2+ + Cl-

The rate law:

kf = k[Pt(II)][Pt(IV)][Cl-]

The mechanism seems to involve rapid addition of free chloride to the Pt(II) complex to form a five coordinate, which then forms an inner sphere complex with Pt(IV)

The Pt centres are then in very similar environments and two-electron transfer takes place. (c.f. Frank Condon restrictions)

Mechanism:

Exchange of *Cl- was found to occur at the same rate as change in optical rotation in the reaction of trans-[Pt(l-pn)2Cl2]2+ with [Pt(en)2]2+

Complementary and Non-Complementary Reactions

All the electron transfer reaction discussed previously are described as complementary.

The oxidant and reductant change their oxidation state by an equal number of units. This termed a Complementary Reaction.

The oxidant and the reductant change their oxidation states by a different number of units. This is termed a Non-Complementary Reaction

Most non-complementary reactions proceed via elementary steps each involving one electron transfers. The most commonly observed kinetic scheme is, for example in chromate ion oxidations (HCr(VI)O4-):

Cr(VI) + Red Cr(V) + Ox

Cr(V) + Red Cr(IV) + Ox

Cr(IV) + Red Cr(III) + Ox

Applying steady-state approximation to Cr(V) then the following rate law can be derived:

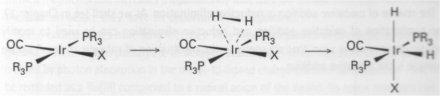
Oxidative Addition

(MORE DETAIL IN ORGANOMETALLICS NOTES)

d8 uses non-bonding axial electron-pair to bond to Lewis Acid, and moves to d6.

This reaction is shown as concerted, since H2 does not have a good leaving group, so no charge separation will occur. H-I would react in a more stepwise fashion, and this would not guarantee a cis product.

It is initiated by:

1) non-polar addition

2) nucleophile attack on a C by lone pair

3) stepwise radical addition

Rate Law:

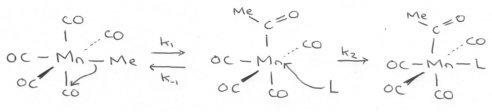
Alkyl Migration

(MORE DETAIL IN ORGANOMETALLICS NOTES)

This mechanism is known by the negative ΔS term (a ligand must be added to the complex) and that making CH3 more electron-withdrawing slows the reaction, showing CH3 is a nucleophile.

Conclusive evidence is the formation of a trans product, which indicates the migration of Me as opposed to CO insertion. This was measured by using labelled CO ligand. Ratios are expected to be 25% trans, 50% cis and 25% unlabelled for the Mn(CO)4(*CO)Me compound (since it forms Mn(CO)4(COMe)(L), *CO ligand may be lost, trans, or one of two cis positions).

Clearly the ligand’s nucleophilicity is a factor in the rate, unless it is very highly concentrated. Other factors that may affect this reaction is the nature of the metal, such that it strengthens the M-Me bond (often due to increased size / overlap – 2nd/3rd row metals). This slows the rate determining step.