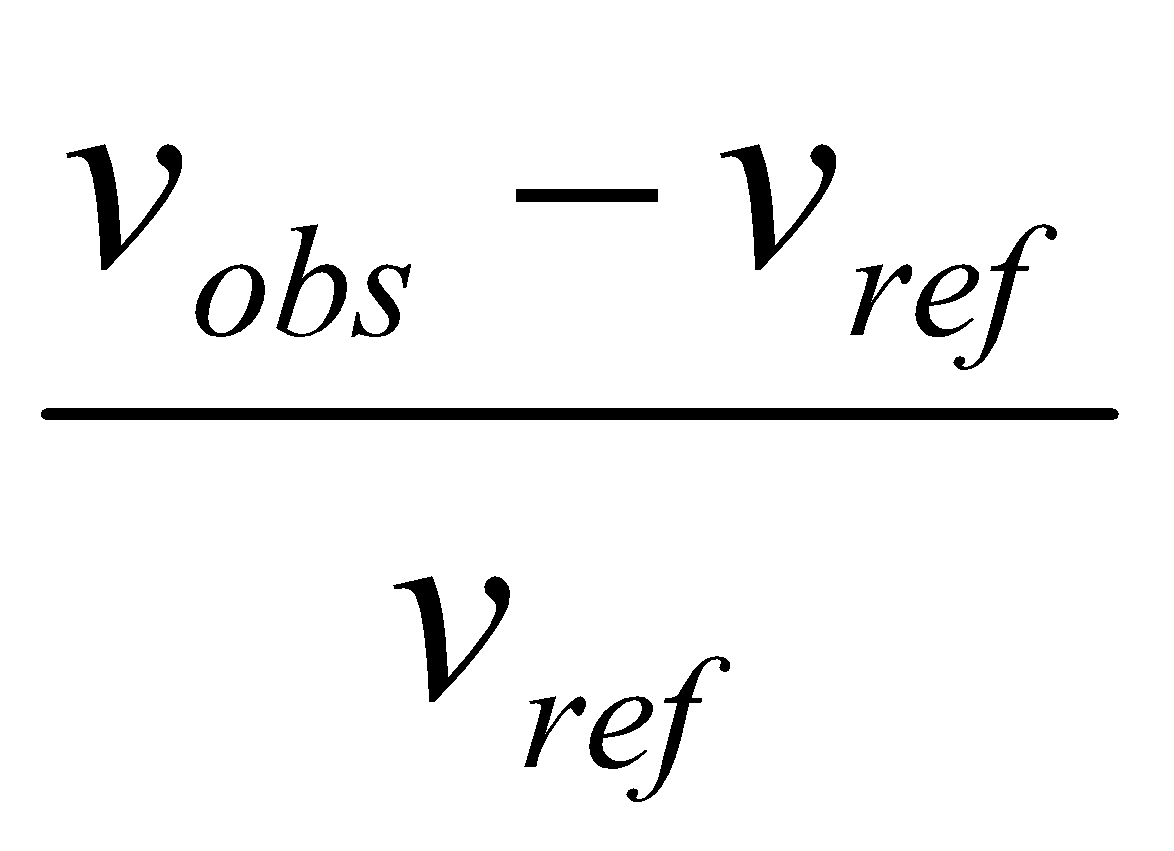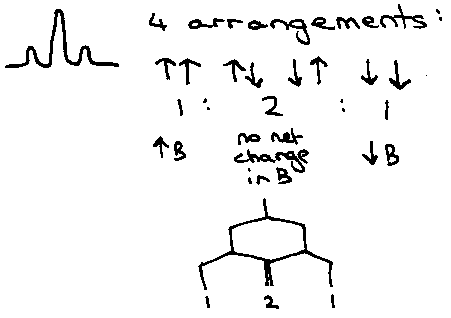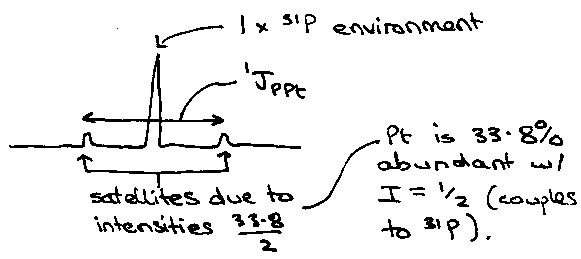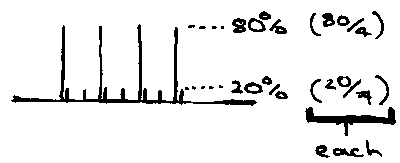General Inorganic NMR Notes

Basic Principles

Nuclei possess a magnetic moment when spin quantum number, I, is non-zero. In the absence of a magnetic field all magnetic states are degenerate, but in a field there are a number of allowed orientations:

m = I, I-1, … -I

i.e. 2I + 1 possible orientations.

The selection rule that applies is Δm = ±1

I = ½ → m = ± ½, and the difference corresponds to the difference in energy of the states:

ΔE = γhB/2π

where B is the magnetic field strength, and γ is the gyromagnetic ratio for the nucleus in question.

From ΔE = hv, the frequency is thus given by:

v = γB/2π

This is typical in the radiowave region of the electromagnetic spectrum. The magnetic field usually is between 2 and 14 Tesla.

Suitability of a Nucleus for NMR Studies

The ease with which an NMR signal can be observed for a particular nucleus with spin quantum number I and abundance A is determined by its receptivity, measured with respect to the 1H nucleus, DXH, where:

Nuclei with I = ½ give higher resolution spectra than quadrupolar nuclei (I > 1) because the latter are typically subject to more efficient (rapid) relaxation.

The signal intensity S is given by:

S = γ4B02NB1g(v)/T

Where N is the number of nuclei sampled, B1 is the field due to the applied radiofrequency radiation, and g(v) is the lineshape function.

Hence,

• S  N (large sample and desirability of high isotopic abundance).
• S  γ4 (signals due to nuclei with large γ easiest to observe).
• S  B02 (advantage of maximum B0).
• S  1/T (low temperatures give enhanced intensity, in principle).

Parameters to be Measured

• Number of resonances identifying the number of structurally distinct nuclei.
• Relative intensities of resonances identifying relative numbers of nuclei in each set.
• Chemical Shift of each resonance defining the shielding of the nucleus, measured as a dimensionless parameter with respect to an appropriate reference.

Frequency separations between resonances (chemical shifts) vary linearly with B0 and hence the Larmor Frequency v.

• Multiplet Structure due to Spin-Spin coupling indicates I and number of nuclei to which a given nucleus is coupled.
• Spin-Spin Coupling constants, nJ, given by the frequency separation (in Hz) between adjacent components of a multiplet. n denotes the number of bonds separating the two nuclei involved. This parameter is invariant with respect to B0 and the Larmor Frequency.
• Linewidths and Lineshapes. The linewidth of an NMR signal depends ultimately on the mechanism and rate of relaxation. There is an inverse relation of linewidth to Relaxation Time. Two such times are important:

• T1, the spin-lattice relaxation time, relates to energy transfer from the nucleus to its surroundings with a change in the component of the magnetisation parallel to B0.
• T2 the spin-spin relaxation time, relates to energy redistribution between spins with a change in the components of the magnetisation perpendicular to B0.

For non-viscous fluids T1 ≈ T2. For viscous liquids and solids T1 >> T2.

Chemical Shift

The effective magnetic field experienced by the nucleus is not equal to the external field, B0. This is due to the motion of electrons surrounding the nucleus – the induced field. This leads to the phenomenon known as shielding:

Beff = B0(1-σ)

Where σ is the shielding constant, and this depends on environment.

Ramsey Formulation of Shielding - σ = σd + σp , i.e. diamagnetic and paramagnetic contributions to the shielding.

Thus, energy and hence frequency for transitions depends on the characteristic environment.

σ is small, so usually convert:

δ = 106 x ,

so

δ = 106 x Δv / (spectrometer frequency)

Each nucleus has an independent reference compound to compare to, e.g. 1H → (CH3)4Si, 19F → CFCl3.

Increased shielding leads to Beff dropping, and so follows the frequency. Thus the peak shifts to a lower chemical shift value.

Increased chemical shift means less shielding around the nucleus = “deshielded”.

Consider HI vs. HF (1H NMR), peaks at -13.5ppm vs. 1.9ppm.

The proton in HF is more deshielded, since the electronegativity of F is higher than for I, so less electron density is found around the H in HF.

Chemical Environment

Shielding of the nucleus is influenced by the types of atoms around it, as shown by the previous example. These each give rise to different chemical shifts, e.g.

Si(CH2CH3)4 – 2 environments for 1H (CH3 and CH2), 2 environments for 13C (C nearest Si and C furthest from Si) and 1 environment for Si.

Similarly, for IF5, the 4 equatorial F atoms are in a different environment to the axial one, as they are trans to other F’s, while the axial one is trans to a lone pair.

This is often useful, as it allows distinguishing of stereoisomers, e.g. cis/trans, mer/fac, etc.

Integration

This corresponds to the area under the peaks, e.g. IF5 has 5 F atoms, but the 4 that are equatorial (in the same environment) will superimpose their peaks, and so be 4 times the height of the axial F.

However, this does not always accurately determine the number in the environment, due to other factors, e.g. varying rates of relaxation of nuclei, or fluxionality.

Coupling

Non-equivalent magnetically active nuclei will couple to each other, if close enough.

Because the coupling is mutual, the degree of splitting seen on the 1H spectrum is the same as that on the 19F spectrum (same coupling constant).

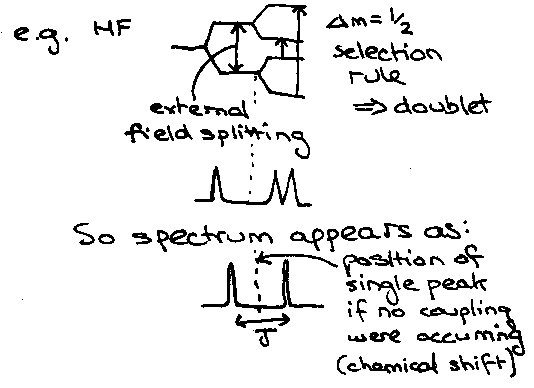
HF2- -

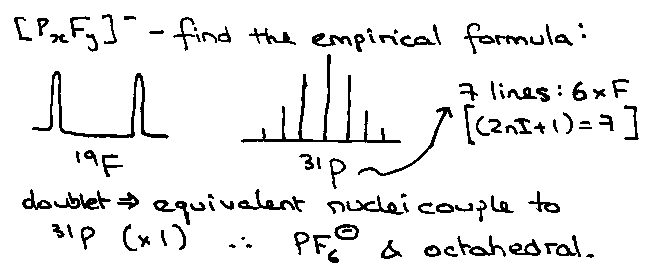
In general, any nucleus will couple with every other magnetically active nucleus in the molecule, providing they are chemically non-equivalent to give rise to a pattern consisting of (2nI+1) lines.

e.g. HF2- -

2F nuclei couple to 1H, so 2x1x0.5 + 1 = 2 lines in 19F.

1H nucleus couples to 2F, so 2x2x0.5 + 1 = 3 lines in 1H.

Intensities can be approximated using Pascal’s Triangle.

Example,

How far can coupling go?

Spatially, not far – but bonds (e-density) favour extended coupling. Usually indicate the number of bonds when quoting the coupling constants, e.g. for PF6-, 1JPF, for H-C-C-H, 3JHH.

Affecting the value of Coupling Constants –

Many factors, e.g. gyromagnetic ratios of nuclei, distance, bonding, angular arrangement and geometry. The latter is particularly useful for stereochemical assignment (e.g. trans usually lot larger than cis, as trans allows interaction via the same orbitals – more direct mechanism for interaction).

Labelling Spin Systems

Identify type and number of spin active nuclei. Coupling constants << chemical shift differences, and this makes it easier to interpret. This is called a first order system.

These use letters close in alphabet to describe nuclei that resonate at similar frequencies and letters far apart for those that don’t.

e.g. Cl3Si(OCH2CH3) – triplet + quartet. Similar resonance frequencies, therefore A2B3 system. This is also true for e.g. CF3CF2Cl or M(PR3)5.

IF4 = AB4.

Well separated shifts are for example HF (AX system) or PF2Cl (AX2).

Magnetic vs. Chemical Equivalence

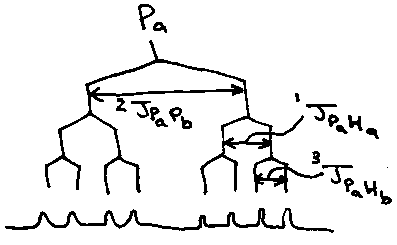
e.g. H2P2O52-

Would expect 1 proton 1 P environment, as Ha/Hb and Pa/Pb are chemically equivalent.

However, Pa couples to Ha differently to Pa coupling to Hb (1 bond vs. 3 bond). The same is true for Pb. Hence, they are magnetically non-equivalent. This is termed a A’XX’ system.

Magnetically non-equivalent nuclei may couple, so the 31P NMR appears as a doublet (Pa←→Pb) of doublets (Ha) of doublets (Hb).

The same kind of pattern is seen in the 1H NMR (doublet of doublets of doublets).

Decoupling

This is used when interpretation is difficult due to larger number of couplings / shifts. This is usually the case when there are many protons on ligands in 13C or 31P NMR.

It is achieved by providing energy over a range of frequencies that cover the proton resonances, and this saturates any transitions that cause coupling. The terminology is usually written as 13C {1H} (which means 1H has been removed).

Spin-dilute Systems

Many elements have one some isotopes which are spin active, e.g. 13C (1.1%). This particular case has such a low abundance that homonuclear coupling is practically observable.

As an example, take Pt(PEt3)2Cl2:

Non-Spin-1/2 Systems

I > ½ means that the nuclei possess a magnetic quadrupole moment. This leads to broad peaks (harder to interpret).

For example, 11B I = 3/2 implies that the quantised energy levels correspond to m = 3/2, 1/2, -1/2, -3/2, which gives 3 allowed transitions. All of these occur at the same energy, so single peak for a single non-coupling 11B nucleus.

But, 4 allowed orientations affects the pattern observed when coupling.

e.g. BH4- (Tetrahedral, equivalent H’s).

This has 10B and 11B coupling to 4 H’s.

11B (80%, I=3/2) has 1H NMR showing 4 lines [(2nI+1) = 2 x 1 x 1.5 + 1 = 4]. Each of the 4 possible m’s equally likely for 11B nucleus, so expect 4 equal intensity lines (1:1:1:1).

10B (20%, I = 3). 1H (2nI+1) = 7 lines.

These combine on the spectrum as:

Chemical shifts are likely to be very similar, but coupling constants differ due to different gyromagnetic ratios.

The 11B NMR consists of one boron resonance coupled to 4 equivalent H nuclei (5 lines in a binomial intensity pattern). The 10B NMR shows the same pattern, but only a quarter of the intensity of the 11B (80% vs. 20%).

Exchange Processes

This offers a likely explanation when fewer lines than expected are seen.

e.g. FeI(CO)2Cp – expect different environments for the H’s on the Cp ring, as some are over the CO ligands, while others are nearer the I. However, the Cp ring rotates around the central axis rapidly (within the lifetime of the NMR experiment). Thus, they all appear equivalent.

In general, if τ is the lifetime of a molecule in a particular conformation, then its energy will be uncertain according to:

ΔE ≈ h/2πτ.

When this energy corresponds to the difference between resonance frequencies (2πΔv) of the two states, a single broad peak is observed.

If lifetime is much greater than equivalent frequency separation, the uncertainty is smaller and so 2 resonances are observed. Thus,

τ << 2πΔv gives a sharp singlet (averaged).

This is often seen in transition metal systems, e.g. alkene complexes where the ligand rotates about its η2 bond.

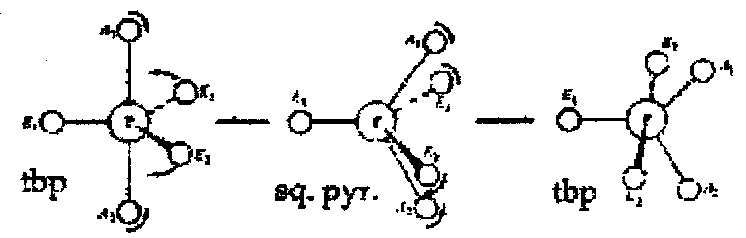
Also common in trigonal bipyramidal systems (e.g. PF5) – flips between 2 forms via square based pyramid structure (Berry pseudorotation).

If nuclei (resonances separated by Δv) are in chemical exchange with each other, the resultant spectrum depends on the rate of exchange, k:

• In the limit of slow exchange, k << Δv – separate sharp resonances are observed.
• In the coalescence region, k = Δv – peaks have broadened and coalesced to a single line.
• In the limit of fast exchange, k >> Δv – broad line has narrowed to a sharp line at δnv.

Typical spectra of [Fe(C5H5)(CO)2]2 – cis ↔ trans isomer interconversion –

Relaxation Processes

Return of perturbed higher energy states to ground state.

There are 2 methods for this – spin-lattice relaxation (where energy is given up to surroundings) or spin-spin relaxation (energy goes to other spin systems in the molecule).

Typically, both are about 1 second for liquid phase NMR.

Spin-lattice relaxation can be affected by e.g. viscosity – slows motion for collision with other molecules to release the energy.

Spin-spin relaxation can be affected by the environment, e.g. 13C relaxes slowly, but protons to couple to speed this up (hence no integration for 13C NMR).

Also, paramagnetic or quadrupolar nuclei can result in very fast relaxation. This leads to the broad peaks, due to the Heisenberg Uncertainty Principle.

This is not always the case though, as it depends on symmetry. Highly symmetric (e.g. octahedral or tetrahedral) compounds relax less efficiently and give sharp peaks.

Structure Determination

The most important tools for this are chemical shift (symmetry in their location) and scalar couplings (symmetry about chemical shift), and intensity (relative).

Also, coupling is reciprocal – coupling constant for A-B in A’s spectrum will be the same value as in B’s spectrum.

Also, it is important to watch out for satellite peaks – coupling arising from coupling to non-100% abundant magnetically active nuclei.

General Trends in Chemical Shift

Usually due to effects on shielding, such that as shielding constant increases, chemical shift decreases, i.e. to less positive / more negative values.

Geometry – affects environment, e.g. axial / equatorial in PF3R2.

Also, cis/trans or mer/fac isomerism.

Electronegativity, Charge & Oxidation State – all affect the electron density around nucleus, so as electron density decrease the shielding constant falls, so the chemical shift rises. This occurs for high electronegativity, positive charge, and high Oxidation State.

Coordination Number – increased coordination causes a fall in chemical shift. This is due to increased electron density around M by more M-L bonds.

Coordination Effect on Ligands – usually small coordination shifts due to high shielding from Transition Metal.

Sometimes not though, e.g. strong π-acceptors such as carbonyls deshielded due to a paramagnetic contribution from backbonding.

Coordination Effect on Metal – in addition to the above, also influenced by magnitude of ligand field splitting and nephelauxetic effects. These are often in competition, though tends to follow the spectrochemical series (e.g. CO, PR3 give large downfield shifts).

The halogens are special in this sense – they balance the paramagnetic contribution due to mixing low lying excited states (Downfield) and diamagnetic effect of electronegativity (upfield).

Hence, the late transition metals give shifts: Cl > Br > I, while early transition metals give shifts: Cl < Br < I. This is called inverse halogen dependence.

General Trends in Coupling Constant

Gyromagnetic Ratio – for a given pair of elements, scalar coupling is proportional to product of gyromagnetic ratios (if all other factors constant). A particular example is comparison of 10B vs. 11B (1JBH = 28Hz vs. 80Hz respectively).

Periodicity – J increases down the group. Most easily measured using reduced coupling constant. J will vary randomly due to different nuclei.

2J increases as intervening atom in 2 bond system moves down a group.

s-character in bond – coupling is transmitted via bonds. Only s-electrons have finite density at the nucleus – more easily contact nucleus via bonds with s-character.

Hybridisation – increase coupling with increased s-character of the bond.

Coordination Number – increasing this decreases J – change in hybridisation of central atom (amount of s-character in any given ligand decreases as number of ligands increases).

Electronegativity – J increases with increasing electronegativity due to increased s-character of the bond.

Trans-influence – M-L coupling influenced by other ligands in the complex. D4h with π-acid trans to M-L bond leads to decreased J.

Again this is due to s-character in the bond and s-electron density at the nucleus.

Interbond Angles – affects s-character. Increase bond angle leads to more s hybridisation required (900 = pure p). Therefore increase J with bond angle. For three bond couplings, dihedral angle, φ, also matters – Karplus Equation: 3J = C cos 2φ + B cos φ + A. Thus, 3J greatest near 0o and 180o.

Lone pairs – usually make J more negative. However, lone pair used in coordination means positive contribution. Magnitude of J decreases on coordination.

Oxidation State – J decreases as Oxidation State of nucleus increases.