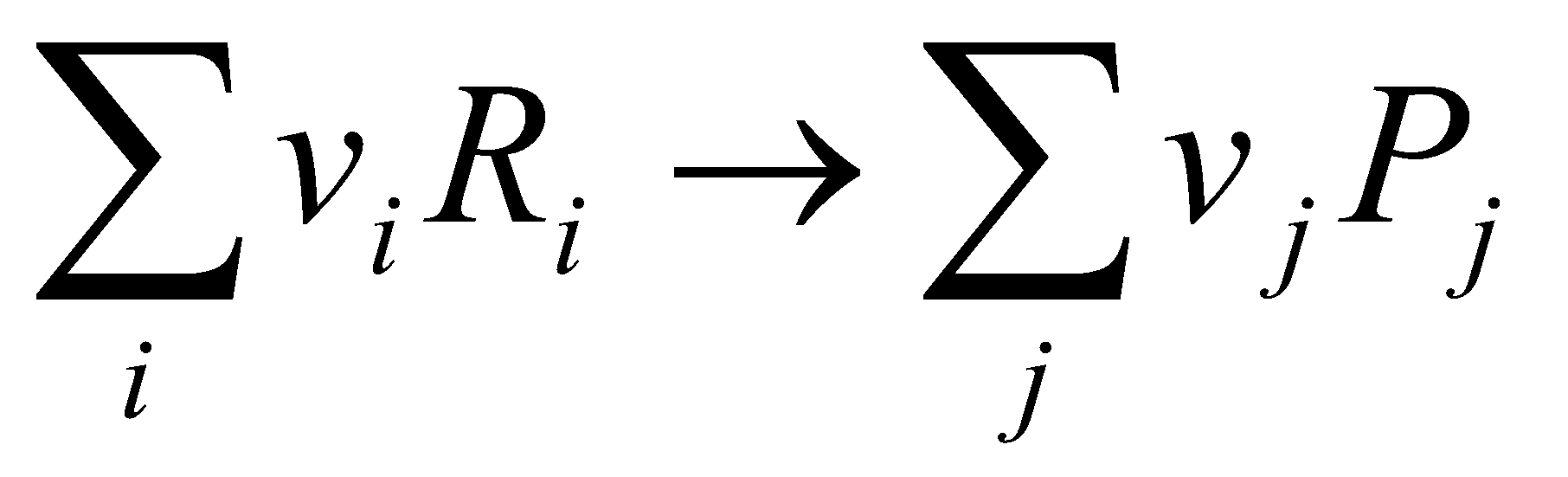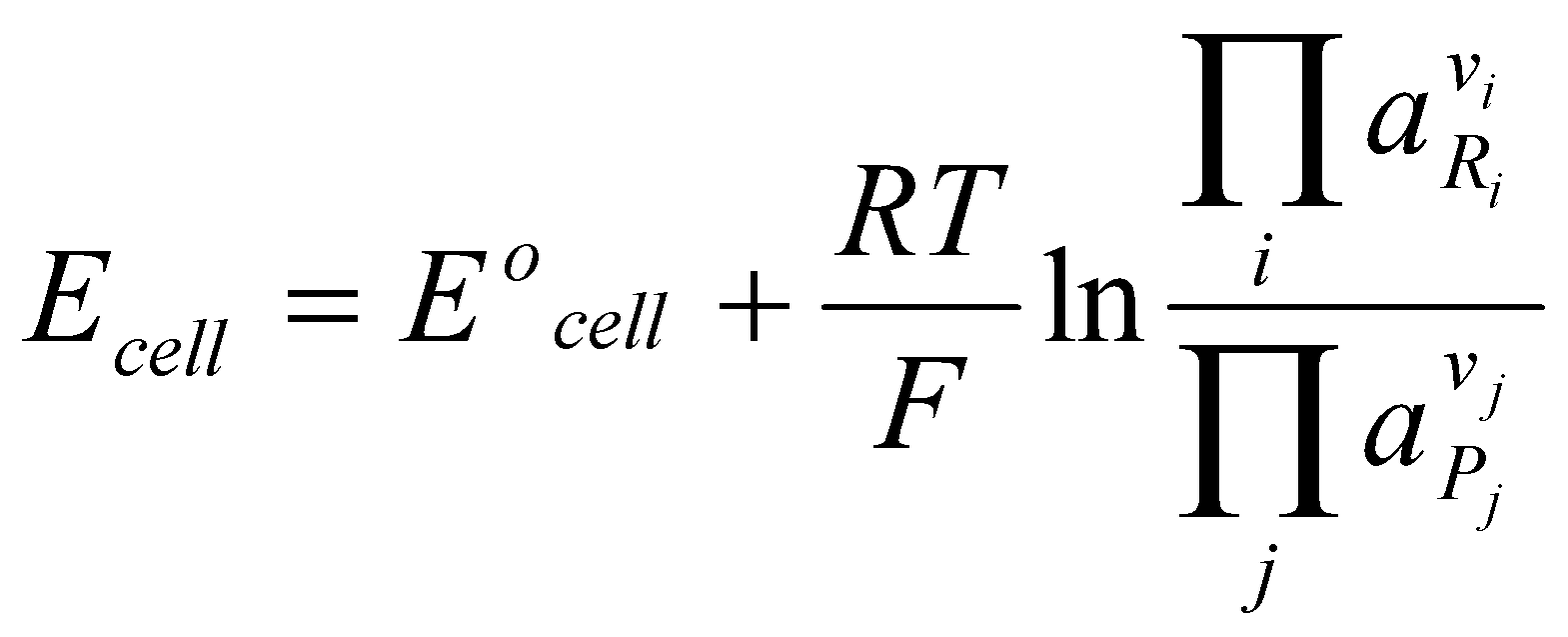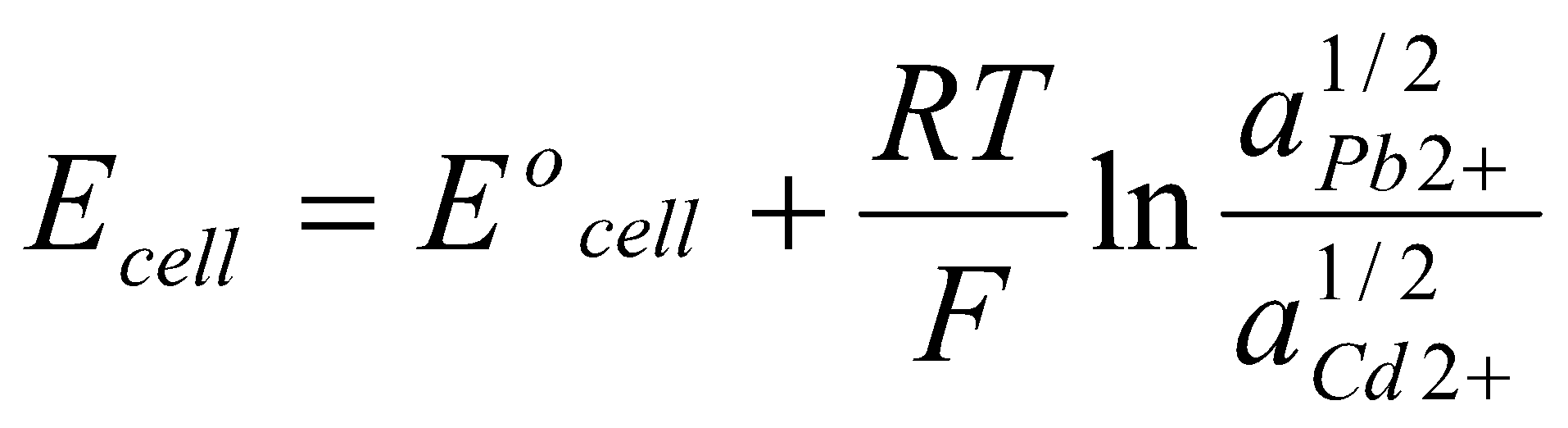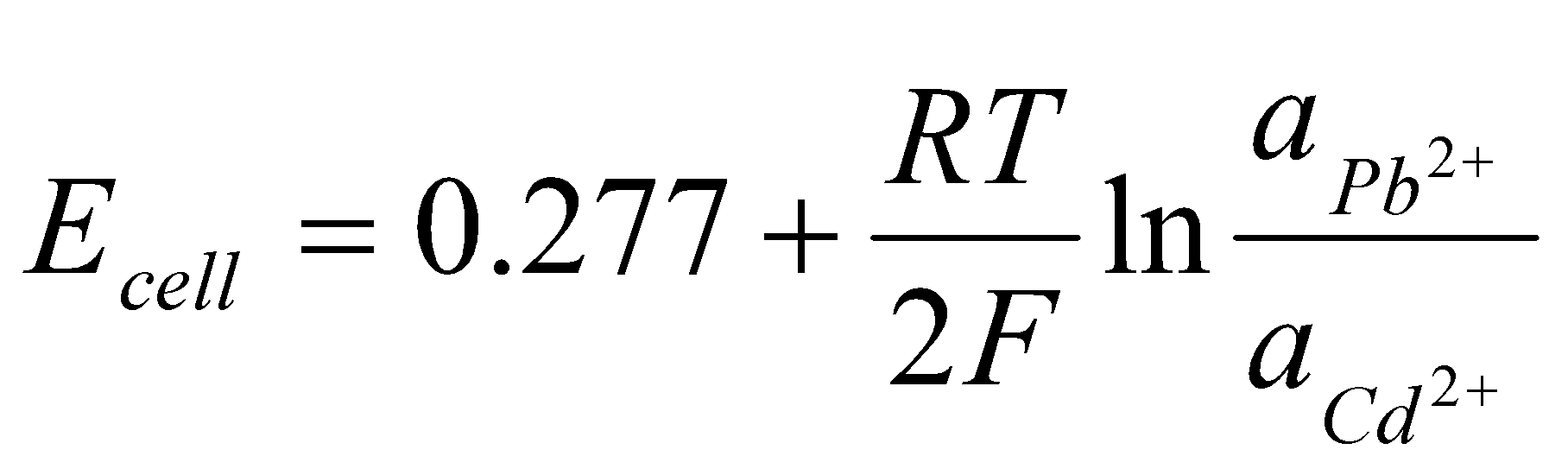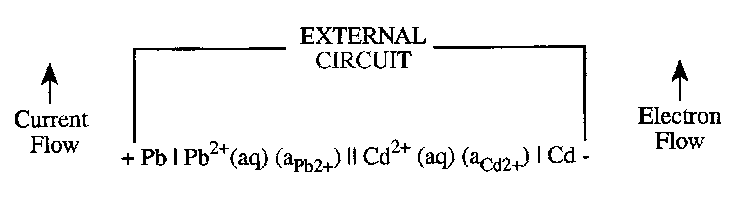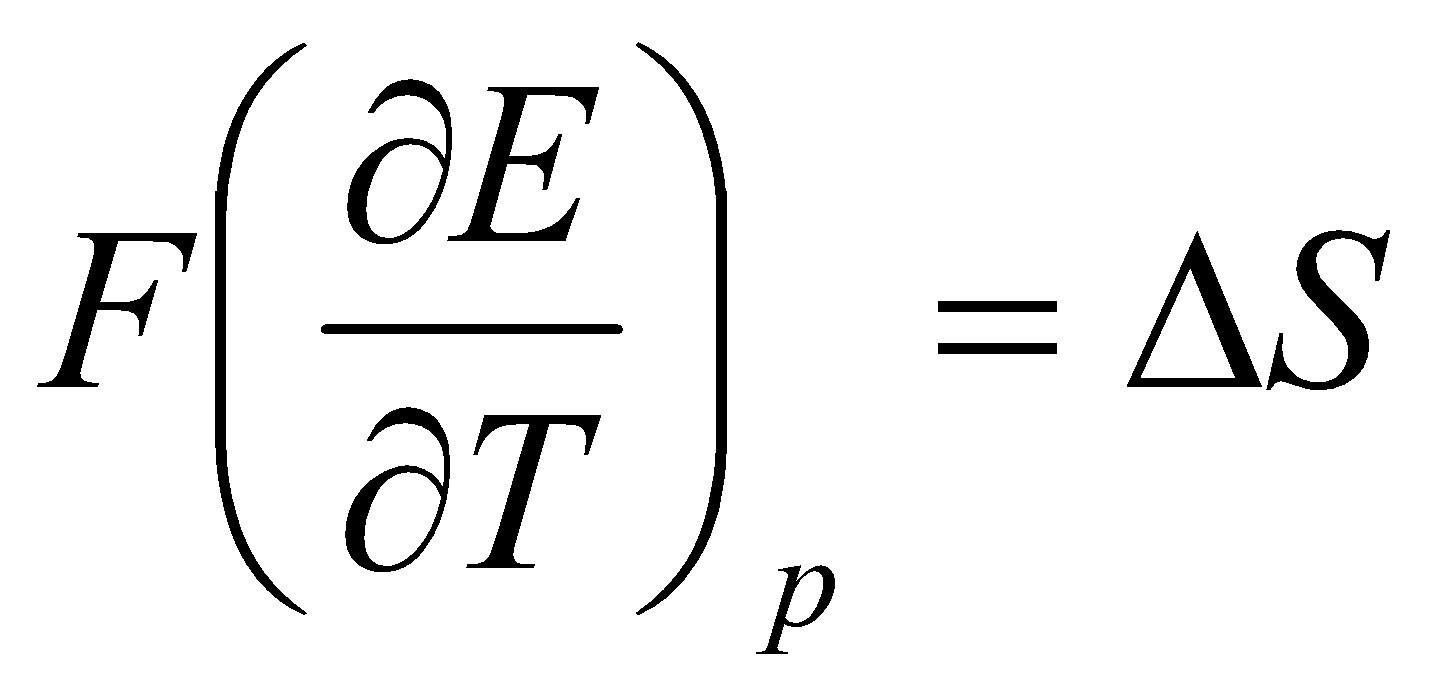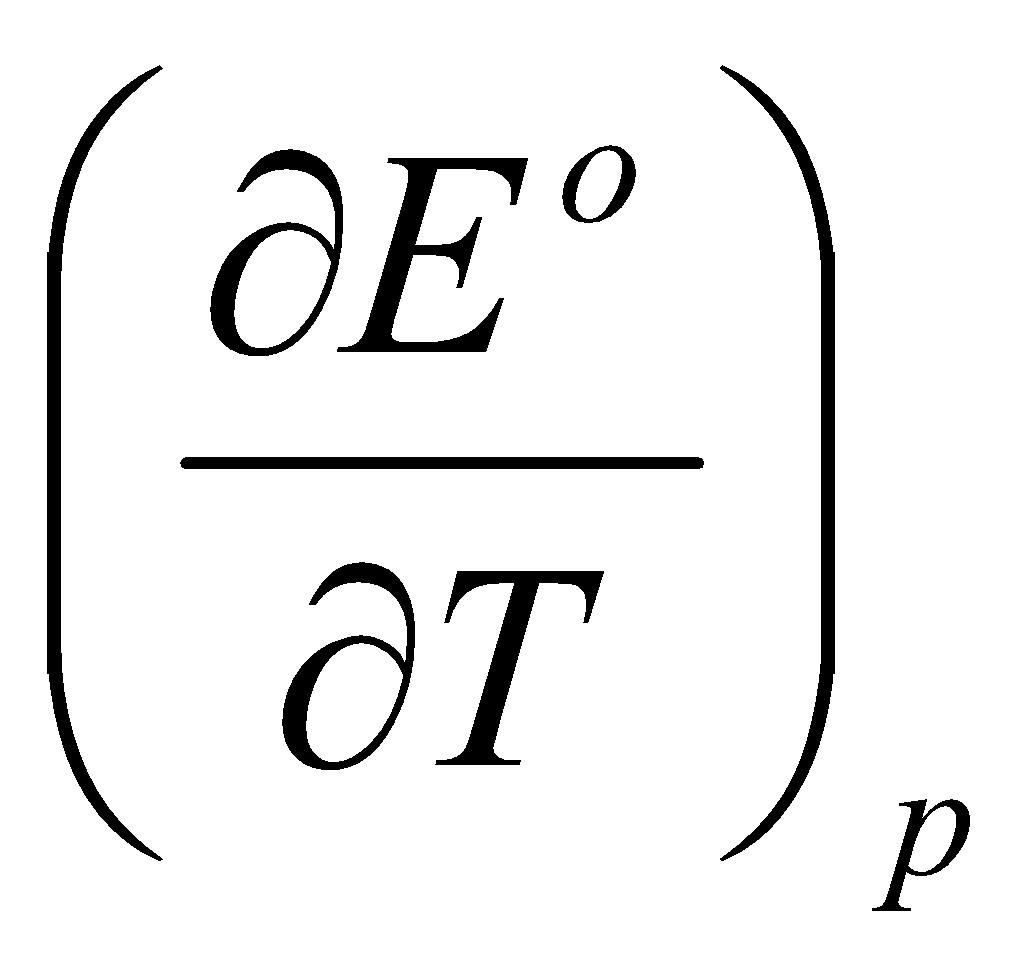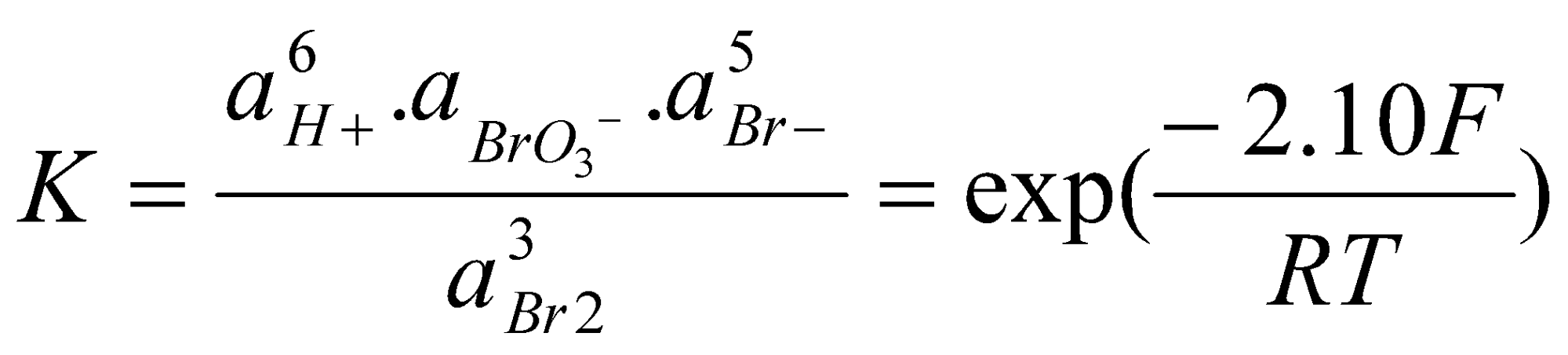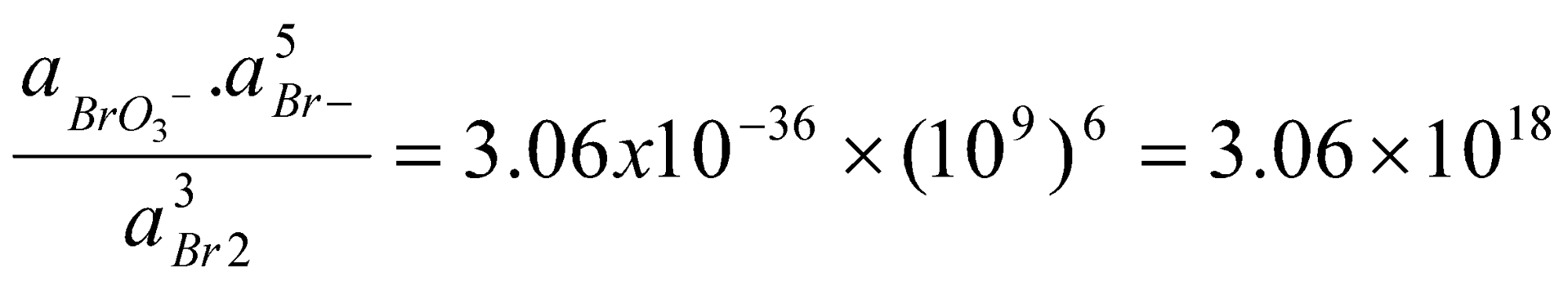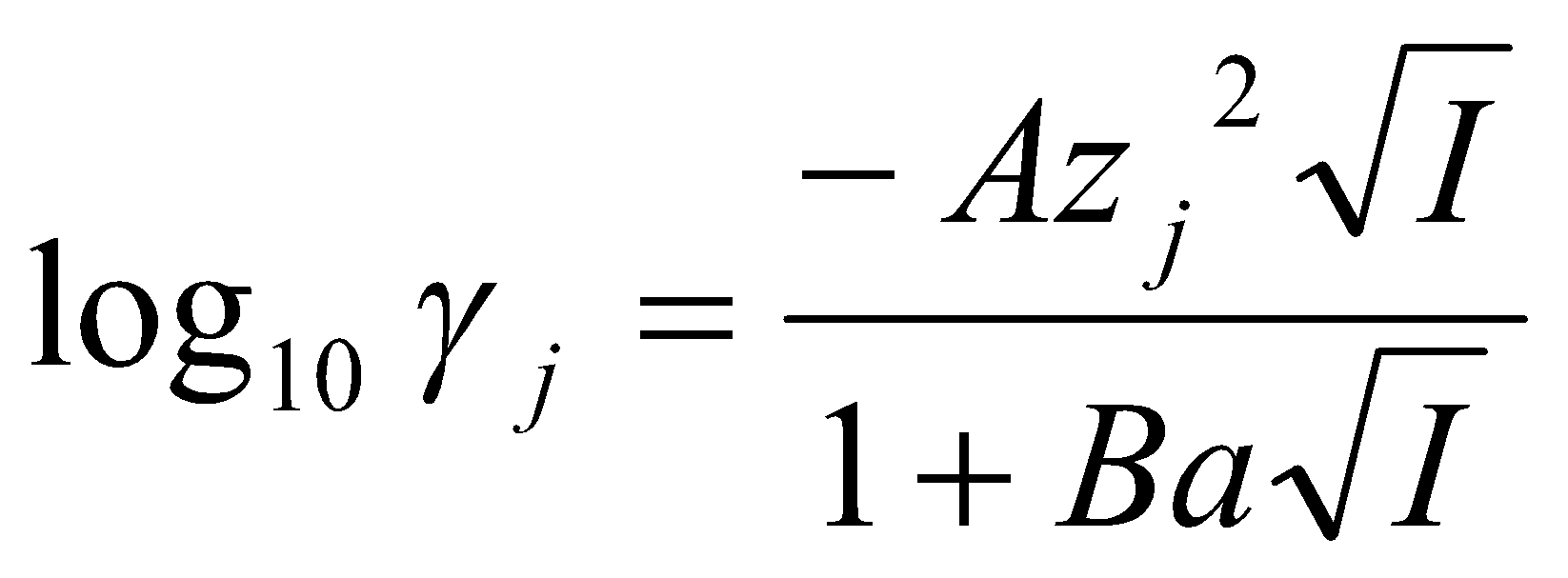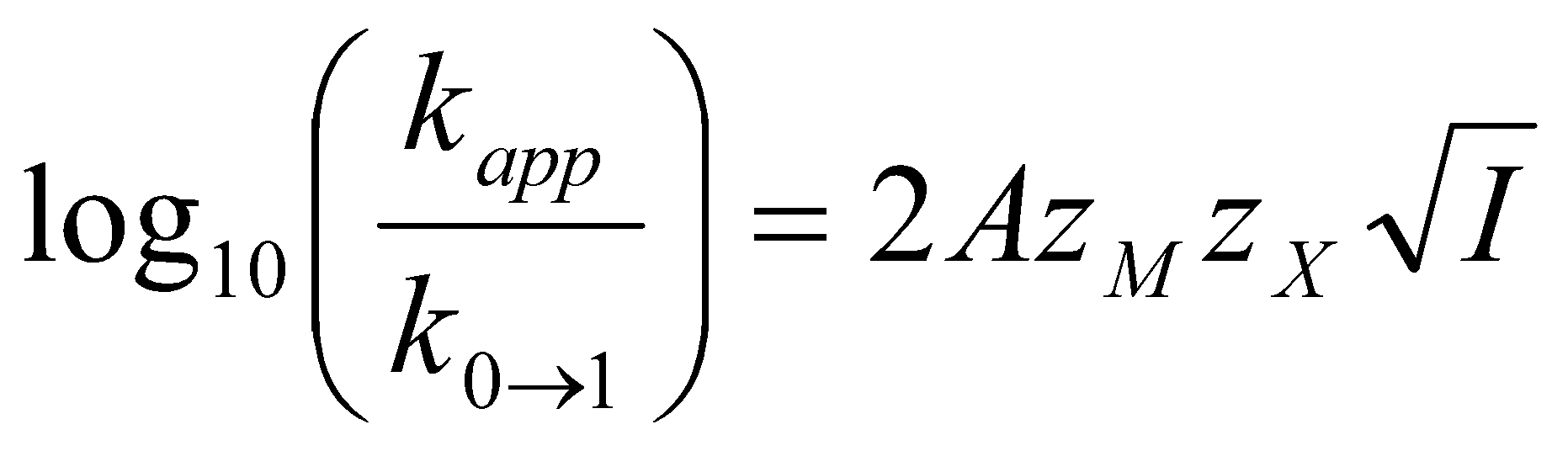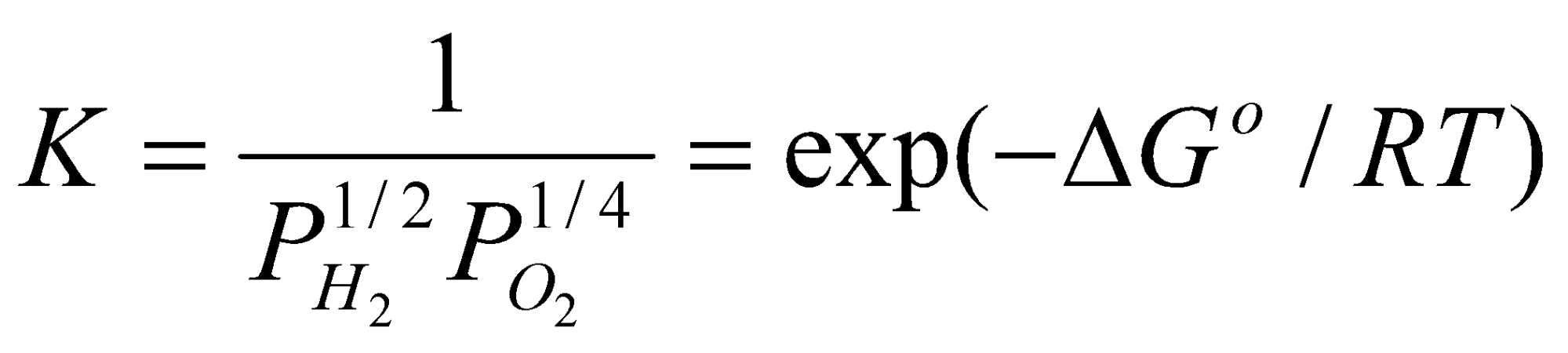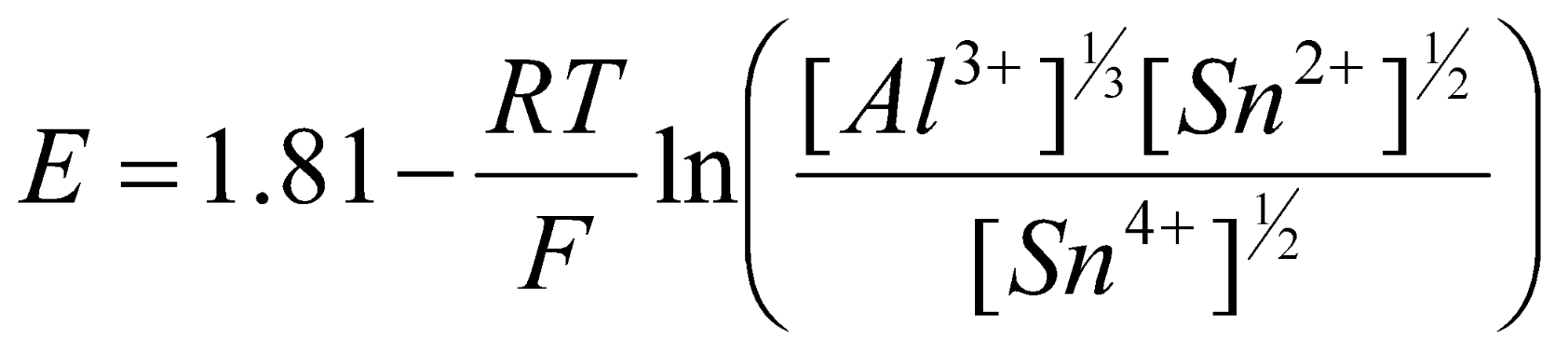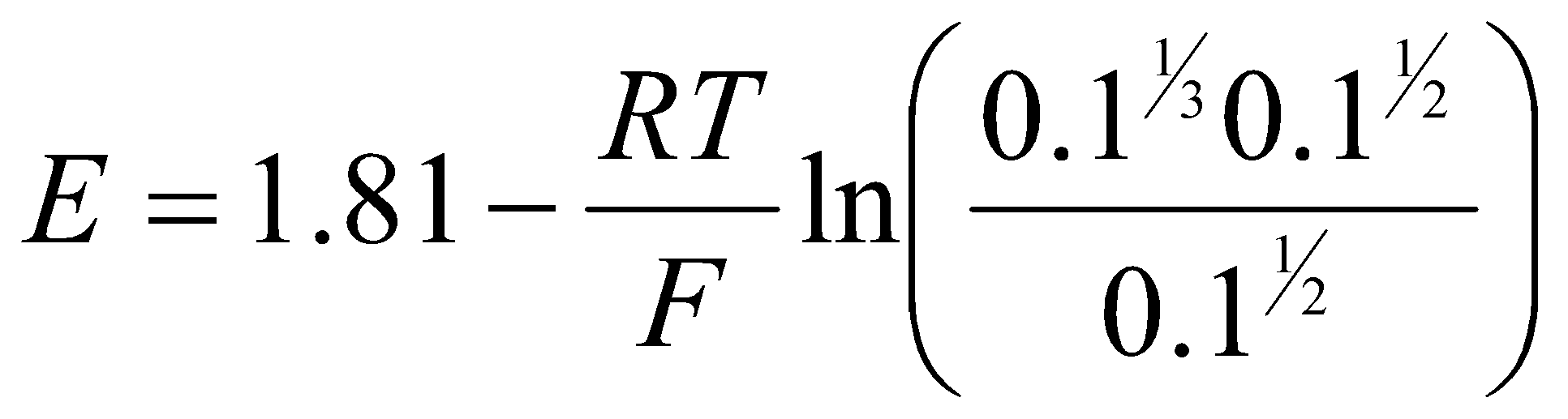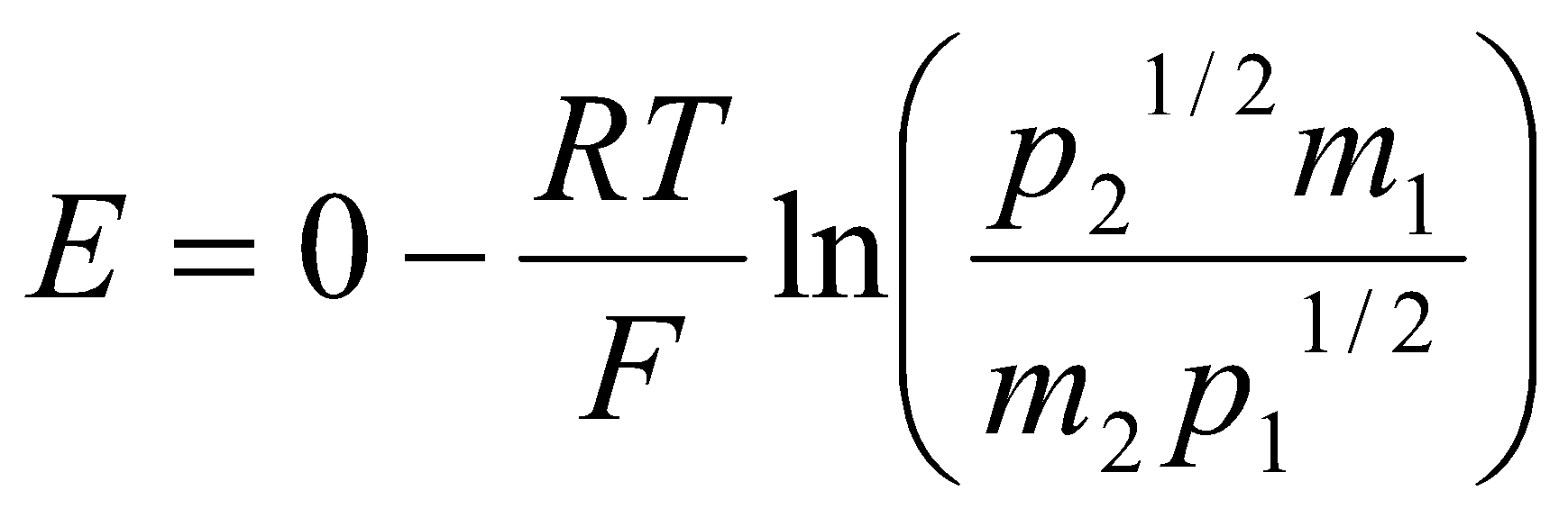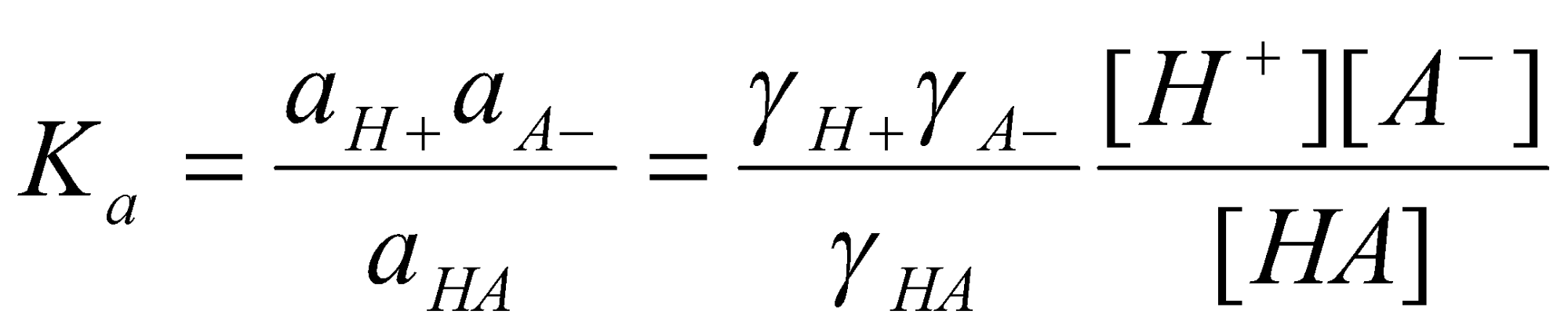Electrochemistry Notes

The Origin of Electrode Potentials

An equilibrium of reduction and oxidation is set up in a solution of Mn+ and Mm+ when a source of electrons (e.g. metal wire) is introduced.

e.g. Fe3+(aq) + e-(metal) ⇌ Fe2+(aq)

Regardless of the favoured direction, it is expected that at equilibrium there will exist a charge separation between the electrode and solution, and hence a potential difference between the two will exist.

Using Le Chatelier’s Principle, we can expect that the concentration of metal ions will influence the equilibrium, and hence the potential. In fact, that ratio of the concentrations of e.g. Fe3+ and Fe2+ is crucial:

φM - φS = constant – RT/F ln ( [Fe2+]/[Fe3+] )

Where φ denotes the electrical potential, and F is the Faraday Constant.

This is the Nernst Equation.

Thermodynamic Description of Equilibrium

Consider the gas phase reaction:

A(g) ⇌ B(g)

The simplest way of keeping track of this system is to note that at equilibrium the reactants and products must have identical chemical potentials:

μA = μB

These can in turn be related to partial pressures, as:

μA = μAo + RT ln pA

At equilibrium:

Kp = pB/pA = exp [ (μAo - μBo)/RT ]

Applying this now to the case where A and B are in solution:

μA = μAo + RT ln xA = μAo + RT ln [A]

where the solutions are assumed to be ideal. Also,

xA = nA/(nA+nB) and [A] = nA/V

This gives rise to two alternative standard states:

1. when mole fractions are used, μo is the chemical potential when x = 1 and so relates to a pure liquid, and
2. when considering concentrations, μo is the chemical potential of a solution of A of unit concentration.

Thermodynamic Description of Electrochemical Equilibrium

The above must be modified for two phases (solution and electrode). Also, it involves the transfer of a charge particle (electrical energy must also be considered). The latter adds a factor of zAFφ to the chemical potential, where zA is the charge on the molecule A.

Deriving the Nernst Equation for the Fe2+/Fe3+ system above, the starting point for this is that at equilibrium, total electrochemical potential of reactants = total electrochemical potential of products. This gives us:

(μFe3+ + 3Fφs) + (μe- - FφM) = (μFe2+ + 2Fφs)

From the revised equation for chemical potential. Rearranging, and applying:

μFe3+ = μoFe3+ + RT ln [Fe3+] (and similar for Fe2+)

we obtain:

φM - φs = Δφo – RT/F ln ( [Fe2+]/[Fe3+] )

Δφo is a constant, containing the two standard chemical potentials + the chemical potential of an electrode in the electrode.

The Nernst Equation and some other electrode/solution Interfaces

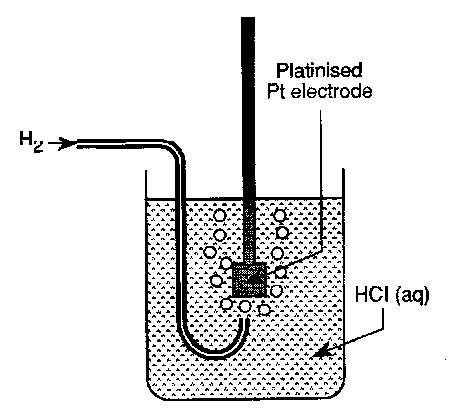
The Hydrogen Electrode

H+(aq) + e-(metal) ⇌ ½H2(g)                        (1)

 

We can derive the Nernst Equation as above:

(μH+ + Fφs) + (μe- - FφM) = ½ μH2

Rearrangement as above gives:

φM - φS = Δφo + RT/F ln ([H+]/pH21/2)

where pH21/2 is equivalent to the “concentration” of H2 gas in terms of chemical potentials.

The Nernst Equation thus predicts that increasing [H+] should make the electrode more positive relative to the solution. This is exactly what we would predict on the basis of the potential determining equilibrium written for this electrode above (i.e. equation (1) is the right way round). Applying Le Chatelier’s Principle, adding H+ shifts the equilibrium to the right. This removes electrons from the electrode, so makes it more positively charged.

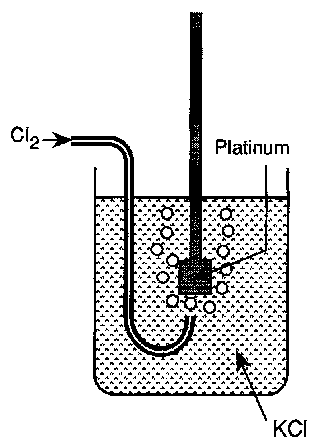
The Chlorine Electrode

½ Cl2(g) + e-(metal) ⇌ Cl-(aq)

Deriving the Nernst Equation exactly as above gives:

½ μCl2  + (μe- - FφM) = (μCl- - Fφs)

i.e.

φM - φS = Δφo + RT/F ln (pCl21/2/[H+])

This predicts that the quantity φM - φs becomes more positive if the partial pressure of chlorine gas is increased, or if the concentration of Cl- is decreased (i.e. the opposite way round to the Hydrogen Electrode).

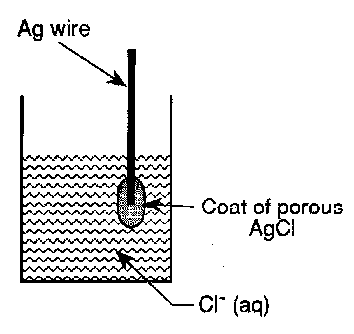
The Silver/Silver Chloride Electrode

AgCl(s) + e-(metal) ⇌ Ag(metal) + Cl-(aq)

The equilibrium is established at the silver/silver chloride boundary. It is therefore important that the silver chloride coat is porous so that the aqueous solution containing the chloride ions penetrates to the boundary to establish equilibrium. We obtain:

(μAgCl) + (μe- - FφM) = (μAg) + (μCl- - Fφs)

Both AgCl and Ag are present as pure solids, hence no terms of the form RT ln [A] appear in their chemical potential equations (only for solutions / gases). This gives:

φM - φS = Δφo – RT/F ln ([Cl-])

Concentrations or Activities?

Activities are introduced to account for non-ideality. More on this below. For now, we can say that activities approximate to concentrations in chemical potential terms, i.e.

φM - φS = Δφo – RT/F ln ([aCl-])

is the most accurate way to express the above. The activity terminology will be used from now on.

Generalising the Nernst Equation for arbitrary potential determining equilibria

For any electrode process:

vAA + vBB + … + e-(metal) ⇌ vCC + vDD + …

The vJ terms are the stoichiometric amounts of each component.

Using the same methodology as for the Fe2+/Fe3+ (and subsequent examples) we find that the Nernst Equation generalises to:

φM - φS = Δφo – RT/F ln (aAvAaBvB…/aCvCaDvD…)

For gaseous components, the activity is replaced by the partial pressures, pJ as above.

Measurement of Electrode Potentials: The Need For A Reference Electrode

Impossible to measure an absolute value for the potential drop at a single electrode solution interface. Need a test electrode and a reference electrode to compare to (to complete the circuit). This is depicted in shorthand notation as:

Reference Electrode | Solution | Test Electrode

The vertical line notates a boundary between two separate phases. The measured potential by the cell is then given by (φtest - φs) – (φref - φs). This works best when (φref - φs) is constant. We can then measure any changes in measured potential directly.

A successful reference electrode must display the following properties:

• The chemical composition of the electrode and the solution to which the electrode is directly exposed must be held fixed. This is because the reference electrode potential will be established by some potential-determining equilibrium and the value of this potential will depend on the relative concentrations of the chemical species involved. If these concentrations change the electrode potential also changes.
• One very important consequence of the requirement for a fixed chemical composition is that it would be disastrously unwise to pass a large electric current through the reference electrode since the passage of this current would induce electrolysis to take place and this would inevitable perturb the concentrations of the species involved in the potential-determining equilibrium.
• It is also experimentally desirable that potential term (φref - φs) attains its thermodynamic equilibrium value rapidly. In other words the potential determining equilibrium should display fast electrode kinetics.

The Standard Hydrogen Electrode

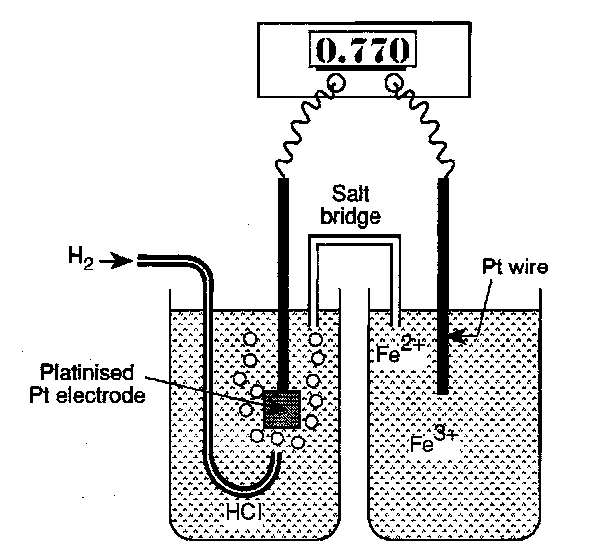
The standard Hydrogen Electrode (SHE) fits the above well. For example, to measure the Fe2+/Fe3+ potential we would use:

The Salt Bridge – tube containing KCl which places the two half cells in electrical contact. One purpose of this is to stop the two different solutions required for the two half cells from mixing. Otherwise, for example, the Pt electrode forming part of the SHE would be exposed to Fe2+/Fe3+ and its potential accordingly disrupted.

• In the SHE the pressure of hydrogen gas is fixed at one atmosphere and the concentration of protons in the aqueous HCl is exactly 1.18M (unity activity of H+). The temperature is fixed at 298K.
• The digital voltmeter draws negligible current so that no electrolysis of the solution occurs during measurement.
• The reference electrode is fabricated from platinised platinum rather than bright platinum metal to ensure fast electrode kinetics. The purpose of depositing a layer of fine platinum black onto the surface is to provide catalytic sites which ensure that the potential determining equilibrium is rapidly established.

Using the Nernst Equation we obtain:

φPt - φS = ΔφoFe2+/Fe3+ – RT/F ln (aFe2+/aFe3+)

φref - φS = ΔφoH2/H+ – RT/F ln (aH+/pH21/2)

The measured potential is:

Δφ = φPt - φref

And can be obtained from the above by simple subtraction:

Δφ = (φPt - φs) - (φPt - φs)

Δφ =ΔφoFe2+/Fe3+ - ΔφoH2/H+ + RT/F ln (aFe3+pH21/2/aFe2+aH+)

Which is often written as:

E = Eo + RT/F ln (aFe3+pH21/2/aFe2+aH+)

The value of Eo is known as the “standard electrode potential” of the Fe2+/Fe3+ couple. This is the measured potential with the SHE (aH+ = 1, pH2 = 1atm) when all the chemical species contributing to the potential determining equilibrium are present at unity activity.

Standard Electrode Potentials (SEP)

A further example is the Cu/Cu2+ couple.

Pt | H2(g) (p = 1atm) | H+(aq) (a=1) || Cu2+(aq) (a=1) | Cu

(The symbol || denotes the salt bridge).

The SEP of the Cu/Cu2+ couple is given by:

EoCu/Cu2+ = φCu - φPt

When measured the potential difference between the copper and platinum electrodes is found to be 0.34V with the copper electrode positively charged and the platinum negatively charged. In writing down potentials a convention is essential so that the correct polarity is assigned to the cell. This is done as follows: with reference to a cell diagram, the potential is that of the right hand electrode relative to that of the left hand electrode, as the diagram is written down. Thus for:

Cu | Cu2+(aq) (a=1) || H+(aq) (a=1) | H2(g) (p=1atm) | Pt

Ecell = -0.34V = φPt - φCu

Pt | H2(g) (p = 1atm) | H+(aq) (a=1) || Cu2+(aq) (a=1) | Cu

Ecell = +0.34V = φCu - φPt

Tabulated values allow the prediction of the potential of any cell formed from any pair of half cells. For example, the cell,

Cu | Cu2+(aq) (a=1) || Zn2+(aq) (a=1) | Zn

Ecell = φZn - φCu

Eocell = EoZn/Zn2+ - EoCu/Cu2+

Note also that it is possible to calculate cell potentials when the activity is non-unity. For example,

Cu | Cu2+(aq) (aCu2+) || Zn2+(aq) (aZn2+) | Zn

Ecell = φZn - φCu = (φZn - φs) – (φCu - φs)

Ecell = (ΔφoZn/Zn2+ + RT/F ln aZn2+1/2) - (ΔφoCu/Cu2+ + RT/F ln aCu2+1/2)

Ecell = (ΔφoZn/Zn2+ - ΔφoCu/Cu2+) + RT/F ln (aZn2+1/2/aCu2+1/2)

Ecell = EoZn/Zn2+ - EoCu/Cu2+ + RT/2F ln (aZn2+/aCu2+)

This is the Nernst Equation for the cell.

The Nernst Equation Applied to General Cell

Following the procedure below (generalised strategy of preceding section):

1. Write down the cell in shorthand notation.
2. Write the reactions at the two electrodes as reductions involving one electron only. Writing the reaction as a reduction means that the electron appears in the left hand side of the equation in each case.
3. Subtract the reaction at the left hand electrode (in the cell as written down) from the reaction at the right hand electrode to find a “formal cell reaction”:

where Ri represents the reactants, Pj the products, and vi and vj are their stoichiometries.

4. The resulting Nernst Equation is given by:

Where Eocell = Eoright + Eoleft (the SEPs of the half-cell reactions as drawn).

Next we illustrate the above procedure for the cell:

Cd | Cd2+(aq) (aCd2+) || Pb2+(aq) (aPb2+) | Pb

Step (ii) gives the reaction at the right hand electrode as:

½Pb2+(aq) + e- → ½Pb(s)

At the left hand electrode the reaction is:

½Cd2+(aq) + e- → ½Cd(s)

Step (iii) and subtracting gives:

½Pb2+(aq) + ½Cd(s) → ½Pb(s) + ½Cd2+(aq)

This is the formal cell reaction.

Step (iv) gives:

Where Eocell = EoPb/Pb2+ + EoCd/Cd2+.

Tables give EoPb/Pb2+ = -0.126V and EoCd/Cd2+ = -0.403V:

Eocell = (-0.126) – (-0.403) = +0.277V

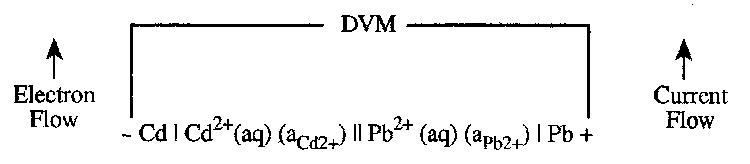
It should be noted that the formal cell reaction, as introduced in step (iii), depends on how the cell is written down in step (i). For example, the cell:

Cd | Cd2+(aq) (aCd2+) || Pb2+(aq) (aPb2+) | Pb

½Pb2+(aq) + ½Cd(s) → ½Pb(s) + ½Cd2+(aq)

Eocell = +0.277V

In contrast the cell:

Pb | Pb2+(aq) (aPb2+) || Cd2+(aq) (aCd2+) | Cd

½Cd2+(aq) + ½Pb(s) → ½Cd(s) + ½Pb2+(aq)

Eocell = -0.277V

It is thus helpful to distinguish the formal cell reaction from the spontaneous cell reaction. The latter is the reaction that would occur if the cell were shortcircuited. That is, the two electrode were directly connected to each other.

The nature of the spontaneous reaction can be readily deduced since in reality, electrons will flow from a negative electrode to a positive electrode through an external circuit as is illustrated:

Notice that this predicts the Cadmium electrode to be negatively charged and the Lead to carry a positive charge. Electrons therefore pass from the Cd to the Pb. This implies that oxidation occurs at the right hand electrode:

½ Cd → ½ Cd2+ + e-

And reduction at the left hand electrode:

½ Pb2+ + e- → ½ Pb

It follows that the spontaneous reaction is:

½Pb2+(aq) + ½Cd(s) → ½Pb(s) + ½Cd2+(aq)

In general, the spontaneous cell reaction that occurs when the two electrodes are shortcircuited may be established using the protocol set out earlier, and tables of electrode potentials decide which electrode is positive charged and which negatively charged. Electron flow in the external current will always be from the negative to the positive electrode so that an oxidation process will occur at the former and a reduction at the latter.

The relation of Electrode Potentials to the Thermodynamics of the Cell Reaction

Due to the negligible current, electrons are transferred under essentially thermodynamically reversible conditions.

Consider,

If dn moles of electrons flow from the negative electrode, then dn moles of the following reaction will occur:

 ½Pb2+(aq) + ½Cd(s) → ½Pb(s) + ½Cd2+(aq)

Associated with this will be a change dG in the Gibbs Free Energy of the cell.

dG = dwadditional

where dwadd corresponds to the work done (other than pdV work) in the process. In the above scheme the only contribution to this quantity is the work done in transferring the charge (-Fdn Coulombs) through the external circuit across a potential difference of Ecellvolts. It follows that:

dG = dwadd = (-Fdn)Ecell

For each mole transferred:

ΔG = - FEcell

Where ΔG refers to the reaction:

½Pb2+(aq) + ½Cd(s) → ½Pb(s) + ½Cd2+(aq)

If the cell components are at unit activity, then:

ΔGo = - FEo

It can therefore be seen that the measurement of cell potentials provides information about free energy changes. Furthermore, since:

dG = Vdp – SdT

It can be concluded that:

Combining this with ΔHo with ΔGo + TΔSo gives:

ΔHo = - FEo + TF

i.e. the entropy and enthalpy of a cell reaction can be obtained from the cell potential and its variation with temperature.

Standard Electrode Potentials and the Direction of Chemical Reactions

Eocell = Eoright + Eoleft

ΔGo = - FEo = - RT ln K

Hence we obtain,

Eo = (RT/F) ln K

We can thus conclude that if Eo is greater than zero K will be greater than one, and if Eo is negative K will be less than unity for the cell reaction. For example, we consider the SEP of a metal/metal ion couple as noted:

Pt | H2(g) (p=1atm) | H+(aq) (a=1), Mn+(aq) (a=1) | M

The formal cell reaction will be:

1/n Mn+(aq) + ½H2(g) → 1/n M(s) + H+(aq)

 and so the SEP of the metal/metal ion couple indicates whether or not the metal will react with H+(aq) to give hydrogen gas. Thus for example in the case of gold, we consider have a SEP for the above of +1.83V and so ΔGo = - 1.83F. It follows that gold will not react with acid under standard conditions to form H2.

Conversely, considering the reaction with Li+, the SEP is -3.04V so that for the above reaction ΔGo = +3.04F, showing reaction of Li with acid is strongly favoured in thermodynamic terms.

The inertness of gold and the reactivity of lithium in aqueous acid predicted in this way is well known.

Generalising the above, it can be seen that if a metallic element M has a SEP for M/Mn+ couple which is negative, then it is possible for M to react with acid under standard conditions to evolve hydrogen. If the SEP is positive then it will be impossible thermodynamically.

A further useful example is seen when taking Cu+ and Cu2+ in aqueous solution. If we consider the disproportionation reaction of Cu(I):

2Cu+(aq) ⇌ Cu(s) + Cu2+(aq)

This can be broken down into two separate reactions:

Cu+(aq) + e- → Cu(s)

Cu2+(aq) + e- → Cu+(aq)

We find that Eo for the former reaction is +0.52V and for the latter is +0.16V. It follows that for the reaction:

Cu+(aq) + ½ H2(g) ⇌ Cu(s) + H+(aq)

ΔGo = -0.52F

Likewise,

Cu2+(aq) + ½ H2(g) ⇌ Cu+(aq) + H+(aq)

ΔGo = -0.16F

The two reactions may be subtracted to give the disproportionation reaction:

Cu+(aq)         +         ½ H2(g)         ⇌         Cu(s)                 +         H+(aq)

minus         Cu2+(aq)         +         ½ H2(g)         ⇌         Cu+(aq)         +         H+(aq)

gives                        2Cu+(aq)                         ⇌         Cu(s)                 +         Cu2+(aq)

For which ΔGo = (-0.52F) – (-0.16F) = -0.36F

And so:

K = aCu2+/aCuaCu+ = 1.2 x 106 mol dm-3

We conclude that the disproportionation reaction is very likely to occur. Indeed Cu(I) disproportionates very rapidly in water, with a lifetime typically of less than one second, forming metallic copper and copper(II) ions.

Standard Electrode Potentials and Disproportionation

Extending the above Copper example to generalise for the reaction:

(a+b) Mx+(aq) ⇌ aM(x+b)+(aq) + bM(x-a)+(aq)

If we consider the separate reactions:

1/b M(x+b)+(aq) + ½ H2(g) ⇌ 1/b Mx+(aq) + H+(aq)        ΔGo = - FEo(Mx+/M(x+b)+)

1/a Mx+(aq) + ½ H2(g) ⇌ 1/a M(x-a)+(aq) + H+(aq)        ΔGo = - FEo(M(x-a)+/Mx+)

Thus,

(ab) times:                1/a Mx+(aq) + ½ H2(g) ⇌ 1/a M(x-a)+(aq) + H+(aq)

minus (ab) times:        1/b M(x+b)+(aq) + ½ H2(g) ⇌ 1/b Mx+(aq) + H+(aq)

gives:                        (a+b) Mx+(aq) ⇌ aM(x+b)+(aq) + bM(x-a)+(aq)

So that:

ΔGo = -abF [ Eo(M(x-a)+/Mx+) – Eo(Mx+/M(x+b)+) ]

It follows that the ΔGo will be negative and the disproportionation favourable if:

Eo(Mx+/M(x+b)+) < Eo(M(x-a)+/Mx+)

In the case of copper, Eo(Cu+/Cu2+) < Eo(Cu/Cu+), and thus disproportionation is favourable.

Standard Electrode Potentials and pH

pH = -log10aH3O+

Consider the disproportionation of bromine:

2Br2(aq) + 3H2O(l) → BrO3-(aq) + 6H+(aq) + 5Br-(aq)

Since Eo(Br2/BrO3-) = +1.48V and Eo(Br-/Br2) = +1.06V, it follows that ΔGo = +2.10F kJ mol-1.

Hence,

Thus, at pH = 0, where aH+ = 1 the disproportionation is unfavourable. However, at pH = 9, we can deduce that:

So that in weakly basic solution the disproportionation becomes thermodynamically possible. Whenever protons or hydroxide ions appear for particular redox couples, the equilibria involved in these couples will be sensitive to the solution pH and by varying this quantity the equilibrium may be shifted in favour of products or reactants.

Thermodynamics vs. Kinetics

We have illustrated the use of electrode potentials in predicting the position of chemical equilibria. The predictions are subject, however, to kinetic limitations.

A classic example of this is Mg(s) dipped in water. Calculations predict this is favourable by -1.53F kJ mol-1, but in practice little or no reaction is observed since a thin film of MgO on the metal surface prevents the reaction taking place. This is also seen for Titanium and Aluminium in water.

Electrode Potentials tell us nothing about the likely rate of the reaction.

Allowing for Non-Ideality – Activity Coefficients

Non-ideal solutions have a chemical potential given by μA = μAo + RT ln aA, where aA is the effective concentration of A in the solution or the activity of A. It is related to the concentration of the solution by the coefficient γ, such that aA = γA[A].

Clearly, if γA is unity, then the solution is ideal. Deviations from unity by γA are a measure of non-ideality. For dilute electrolytic solutions it is possible to calculate γA, involving the use of the Debye-Huckel Theory.

In approaching this topic, it is useful to have some grounding in the Thermodynamics of Solutions, found in the Thermodynamics Notes.

Debye Huckel Theory

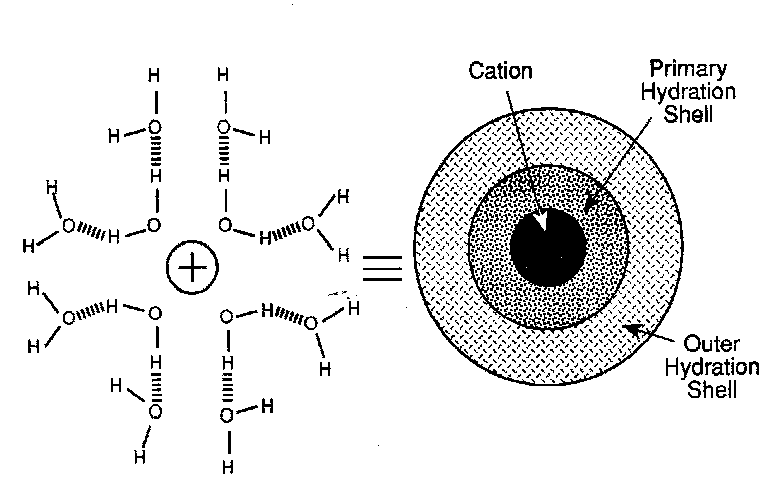
For a dilute electrolytic solution the activity coefficient, γ, is usually less than 1. This implies that the solution is more stable, by an amount RT ln γI, as compared to the hypothetical situation where the ionic charge is “off”. The physical origin of this stabilisation arises from the fact that the anion “sees” more oppositely charged ions than like-charged ions as it moves about in solution. Let us consider the distribution of charge around an ion.

On a time average this must be spherically symmetrical and reflect the fact that there will be a build up of opposite charge around the ion. The magnitude of the opposite charge decreases in a radial direction away form the ion in question. Far away from the ion the charge becomes zero corresponding to bulk solution, sufficiently remote that the ion’s electroneutrality is unperturbed. These are referred to as ionic atmospheres.

We can calculate the charge distribution in the ionic atmosphere around a particular ion, j, and then use this to quantify the stabilisation of the ion. When scaled up for one mole of ions this should be equal to RT ln γj.

This turns out to be a straightforward but tedious exercise in electrostatics, provided some assumptions are made. The result is quite simple.

The deviation from ideality depends on a quantity known as the ionic strength, I, of the solution. This is defined as:

where the sum is over all the ions, i, in solution, ci is the concentration of ion i and zi its charge.

For example, consider a 0.1M solution of MgCl2:

I = ½ [ 0.1 x (+2)2 + 0.2 x (-1)2 ] = 0.3M

The ionic strength here is greater than the concentration.

As a second example consider a 0.1M solution of NaCl:

I = ½ [ 0.1 x (+1)2 + 0.1 x (-1)2 ] = 0.1M

In this case the ionic strength equals the concentration. This is a general result for species of the formula M+X-.

The basic equation of Debye-Huckel Theory is:

log10 γj = - Azj2 √I

where zj is the charge on the ion and A is a temperature and solvent dependent parameter. For water at 25oC, A ≈ 0.5.

In calculating the electrostatic stabilisation conferred on an ion by its atmosphere so as to establish this equation, several assumptions are made:

1. The cause of the solution non-ideality resides exclusively in coulombic interactions between the ions, and not at all, for example, in ion-solvent interactions.
2. The ionic interactions are quantitatively described by Coulomb’s Law for point charge. This presumes that the effects of the solvent is solely to reduce inter-ionic forces by means of the dielectric constant.
3. The electrolyte is fully dissociated and no significant numbers of ion pairs exist. This implies that the external forces between the ions are weaker than the thermal forces in the solution moving ions around, together and apart.

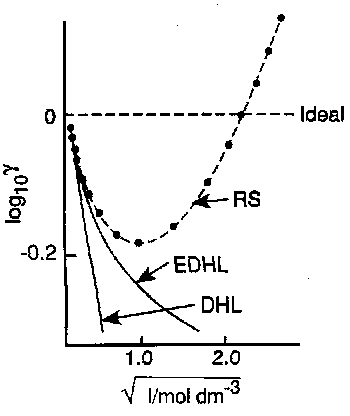
These assumptions work well in dilute solutions, so that for ionic concentrations below ~ 10-2 M the Debye-Huckel Limiting Law works quantitatively.

The Debye-Huckel Limiting Law predicts that the deviation from ideality increases with the square root of the ionic strength, I. It is interesting to consider why this should be, and to focus on the size of the ionic atmosphere. The effective size is the latter is measured by its Debye length, which gives an indication of the distance between any ion and the average location of the charge in its ionic atmosphere. The higher the concentration, the shorter the Debye length, i.e. Debye length 1/√I.

It follows that as the ionic strength increases the distance between the central ion and the charge in the ionic atmosphere shrinks. Accordingly Coulomb’s Law leads us to expect that the electrostatic stabilisation of the ion conferred by the ionic atmosphere increases so that γj becomes smaller and the solution more non-ideal.

Limits of Debye-Huckel Theory

Works well in dilute solution – up to concentrations around 10-2M, but overestimates the deviation from ideality at higher concentrations.

The Extended Debye-Huckel Law is given by the equation:

The constant B is, like A, a solvent and temperature specific parameter, whilst a is the radius of the ion, j. Hence, it is derived without the need to assume point charges (uses spheres of radius a instead). This works at higher concentrations.

Neither of these laws can predict the upturn seen at higher concentrations however. Physically this is because both equations attribute the deviation from ideality to electrostatic forces stabilising each ion and these increase – and the ionic atmospheres shrink – as the ionic strength increases. Some new factor must become important at higher concentrations.

This is because the y-axis no longer relates to the activity coefficient of a single ion, but is the mean activity coefficient, γ±, defined as γ± = (γ+γ-)1/2 for an electrolyte of stoichiometry MX.

It can be seen that the deviation of experiment from the Debye-Huckel Limiting Law is faster for e.g. LiCl when compared to KCl. This implies that the new factor influencing deviation is greatest for Li+. This can be attributed to charge density, which is higher on Li+. As a consequence, Li+ is more strongly hydrated in solution, i.e. deviation from the Debye-Huckel Limiting Law at higher concentrations is due to ion-solvent effects.

Can actually add a cI term to the Extended Debye-Huckel Law to account for this, where c is a solute and solvent specific parameter characterising the salvation of the ions.

Applications of the Debye-Huckel Limiting Law

Solubilities

The solubility of sparingly soluble salts can be slightly enhanced by an increase in ionic strength. For example the solubility product of silver chloride is Ksp = aAg+aCl- = 1.7x10-10 mol2 dm-6 so that in pure water the solubility is approximately 1.3x10-5 mol dm-3. The solubility of AgCl is promoted, a little, by the addition of KNO3.

Mz+Mz-(s) ⇌ Mz+(aq) + Mz-(aq)

Ksp = aMaX = γM[Mz+].γx[Xz-]

= γ±2[Mz+][Xz-]

The cation and anion concentrations will equal one another (=c), so that:

log10 Ksp = 2 log10 γ± + 2 log10c.

Applying the Debye-Huckel Limiting Law then gives:

log10c = ½ log10Ksp + z2A√I.

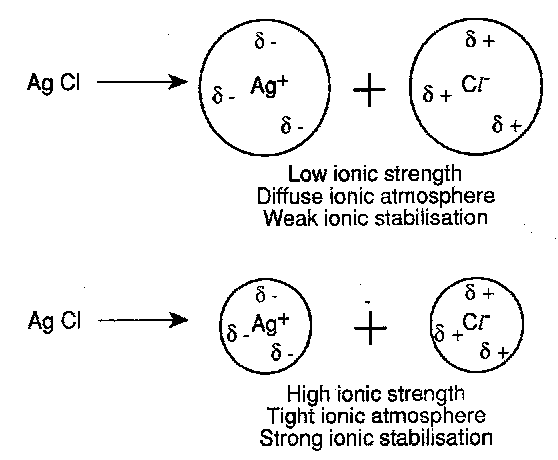
This shows that as the ionic strength is increased the solubility of MX is promoted. It is helpful to ask the physical reason for this, and to focus on the specific case of silver chloride. When AgCl is dissolved into a solution to which KNO3 is progressively added, the Ag+ and Cl- ions will develop ionic atmospheres around themselves which will serve to stabilise the ions. Considering the equilibrium, stabilisation will pull it to the right hand side, so promoting solubility of the silver halide. As the ionic strength of the solute rises, the Debye length of the ionic atmosphere will shrink so that each ion will become closer to the (opposite) charge surrounding it and so the stabilisation is enhanced. Remember though that it will only apply quantitatively to dilute solutions.

The Kinetic Salt Effect

Consider the reaction between two charged species, M and X:

M + X ⇌ { M,X } → products

Where { M,X } is an activated complex or transition state denoted ‡ below. Assuming a pre-equilibrium with reactants M and X prior to reaction to the former with rate constant k, then:

K = a‡ / aMaX = (γ‡/γMγX)([‡]/[M][X])

The rate of reaction will be given by rate = k[‡]

Combining gives:

rate = kK(γMγX/γ‡)

Or,

log10kapp = log10kK + log10γM + log10γX – log10γ‡

When expanding taking into account the Debye-Huckel Limiting law this gives:

log10kapp = log10kK  - AzM2√I – AzX2√I + A(zM+zX)2√I

log10kapp = log10kK + 2AzMzX√I

Or,

where k0→1 is the measured second order rate constant at infinite dilution.

This equation predicts that if we change the ionic strength, I, of a solution by adding an inert electrolyte containing no M or X, and which plays no part in the reaction other than to change the ionic strength, nevertheless the rate of the reaction between M and X can be altered. Bizarrely, if M and X have the same charge, increasing the ionic strength is predicted to increase the rate, while opposite charges gives an anticipated decrease in rate!

The clue to this behaviour lies in the effect of ionic atmospheres, not just on the reactants M and X, but also now on the transition state.

Considering a pair of divalent anions and cations reacting, adding an inert salt supplies ions which provide the reactants with an ionic atmosphere. This will stabilise the ions. In contrast, the transition state, which is neutral, will have no ionic atmosphere and hence its energy will be essentially unchanged. The barrier to the reaction is thus increased.

Two divalent cations reacting, however, means that the transition state carries charge. In this case both the reactants and transition state are stabilised by the ionic atmosphere, and the reaction barrier is now lowered.

More on Electrode Potentials

Suppose we wanted to obtain the value of the standard electrode potential of the cell:

Pt | H2(g) (p=1atm) | H+(aq) (a=1) Cl-(aq) (a=1) | AgCl | Ag

This cell is know as the Harned Cell.

That is equivalent to investigating the standard electrode potential of the Ag/AgCl couple:

EoAg/AgCl = φAg - φPt

In order to proceed with measurement we need to know how to obtain the concentration for unit solution activity. It is necessary to proceed as follows:

The potential of the cell is given by:

E = EoAg/AgCl – (RT/F) ln [ aH+aCl- ]

Where the activities are related to the concentrations by means of activity coefficients γ. If the solution is suitably dilute the Debye-Huckel Limiting Law can be used to predict the ionic activity coefficients:

log10 γ+ = - A z+2 √I

In our example z+ = z- = 1 and A = 0.509, which gives:

E = EoAg/AgCl – (RT/F) ln [HCl]2 – (RT/F) ln γ±2

On relating the activity coefficient to the ionic strength we finally obtain:

E + (2RT/F) ln [HCl] = EoAg/AgCl + (2.34RT/F) √[HCl]

Consequently if we measure the cell potential, E, as a function of the HCl concentration in the region where the Debye-Huckel limiting law applies, a plot of E + (2RT/F) ln [HCl] against √[HCl] should give a straight line with an intercept equal to the standard electrode potential of the Ag/AgCl couple.

The above experiment is a little special in the sense that both electrodes dip into the same electrolyte solution. The latter contains H+ ions which participate (with the hydrogen gas) in establishing the potential at the platinum electrode and also Cl- ions which help produce the potential on the silver/silver chloride electrode. In other cases it is simply not possible to use a single solution. For example, suppose we wished to measure the standard electrode potential of the Fe2+/Fe3+ couple. A single solution cell,

Pt | H2(g) (p=1) | H+(aq) (a=1), Fe2+(aq) (a=1), Fe3+(aq) (a=1) | Pt

is inappropriate since both platinum electrodes are exposed to the Fe2+ and Fe3+ ions. Thus at one of the two electrodes both the Fe2+/Fe3+ and the H+/H2 couples will try to establish their potentials. This is why salt bridges are used.

Worked Examples

Equilibrium Constants

Calculate the equilibrium constants for the following reactions at 25oC in aqueous solutions,

1. Sn(s) + CuSO4(aq) ⇌ Cu(s) + SnSO4(aq)
2. 2H2(g) + O2(g) ⇌ 2H2O(l)

Given the following standard electrode potentials:

½ Sn2+(aq) + e- ⇌ ½ Sn(s)                -0.136V

½ Cu2+(aq) + e- ⇌ ½ Cu(s)                +0.337V

¼ O2(g) + H+(aq) + e- ⇌ ½ H2O        +1.229V

We consider first equilibrium (a) and begin by noting that definition of the standard electrode potential of the Sn/Sn2+ couple implies for the following cell:

Pt | H2(g) (p=1atm) |H+(aq) (a=1) || Sn2+(aq) (a=1) | Sn

the cell potential is EoSn/Sn2+ = -0.136V = φSn - φPt

The strategy from earlier allows us to associate a formal cell reaction with the above cell as follows. The potential determining equilibrium at the right hand electrode is:

½ Sn2+ + e- ⇌ ½ Sn(s)

And at the left hand electrode:

H+(aq) + e- ⇌ ½ H2(g)

Subtracting gives:

½ Sn2+(aq) + ½ H2(g) ⇌ ½ Sn(s) + H+(aq)

For this last reaction:

ΔGo = - FEoSn/Sn2+ = +0.136F

Likewise for the Cu cell,

Pt | H2(g) (p=1atm) |H+(aq) (a=1) || Cu2+(aq) (a=1) | Cu

EoCu/Cu2+ = +0.337V

The potential determining equilibria at each electrode are:

Right Hand Electrode:                 ½ Cu2+(aq) + e- ⇌ ½ Cu(s)

Left Hand Electrode:                H+(aq) + e- ⇌ ½ H2(g)

This enables the formal cell reaction to be deduced:

½ Cu2+(aq) + ½ H2(g) ⇌ ½ Cu(s) + H+(aq)

For which:

ΔGo = - FEoCu/Cu2+ = -0.337F

From these two reactions, subtracting:

½ Cu2+(aq) + ½ Sn(s) ⇌ ½ Cu(s) + ½ Sn2+(aq)

For which,

ΔGo = (-0.337F) – (+0.136F) = -0.463F

and ΔGo = -RT ln Kc

Kc here = [Sn2+]/[Cu2+] = 1x108, so for the original question (1 mol, not ½), the equilibrium constant = 1x1016.

Next we turn to equilibrium (b).

Pt | H2(g) (p=1atm) | H+(aq) (a=1), H2O (a=1) | O2(g) (p=1atm) | Pt

The formal cell reaction can be deduced by subtracting the potential determining equilibria at each electrode, as follows:

Right Hand Electrode:                ¼ O2(g) + H+(aq) + e- ⇌ ½ H2O(l)

Left Hand Electrode:                H+(aq) + e- ⇌ ½ H2(g)

To Give:                        ¼ O2(g) + ½ H2(g) ⇌ ½ H2O(l)

For this reaction, ΔGo = -1.229F

And the associated equilibrium constant:

= 6 x 1020 atm-3/4

Note that the activity of water is absent from the definition of K.

The Nernst Equation

For the following cell:

Al | Al3+(aq) || Sn4+(aq), Sn2+(aq) | Pt

State or calculate at 25oC:

1. the cell reaction
2. the cell EMF when all concentrations are 0.1M and 1.0M (ignore activity coefficients).
3. ΔGo for the cell reaction in (a)
4. K for the cell reaction in (a)
5. The positive electrode and the direction of electron flow in an external circuit connecting the two electrodes.

The standard potentials are EoSn2+/Sn4+ = 0.15V and EoAl/Al3+ = -1.61V

The potential determining equilibria are:

Right Hand Electrode:                ½ Sn4+(aq) + e- ⇌ ½ Sn2+(aq)

Left Hand Electrode:                ⅓ Al3+(aq) + e- ⇌ ⅓ Al(s)

Formal cell reaction:                ½ Sn4+(aq) + ⅓ Al(s) ⇌ ½ Sn2+(aq) + ⅓ Al3+(aq)

When all the potential determining species in the cell are present at unit activity the cell potential is:

Eocell = EoSn2+/Sn4+ - EoAl/Al3+ = (0.15) – (-1.66) = 1.81V

So that for the reaction above: ΔGo = -1.81F = -175kJ mol-1

It follows that the reaction is thermodynamically downhill and is the process which would occur if the cell was short-circuited.

The cell EMF will be given by the appropriate Nernst Equation:

So that when all the concentrations are 1.0M the cell EMF is 1.81V.

When the concentrations are 0.1M,

= 1.81 + 0.02 = 1.83V

The equilibrium constant for the reaction is:

K = [Al3+]⅓[Sn2+]½/[Sn4+]½ = exp (1.81F/RT) = (4x1030 mol dm-3)1/2

 

Last we note the cell polarity will always be:

(-) Al | Al3+(aq) || Sn4+(aq), Sn2+(aq) | Pt (+)

unless tremendous extremes of concentration ratios occur ([Al3+] >> [Sn4+] and [Sn2+] >> [Sn4+]). It follows that if the cell is short-circuited then electrons would leave the aluminium, which would oxidise, and that at the platinum electrode Sn4+ ions would be reduced.

Concentration Cells

Consider the following cell:

Pt | H2(g) (p1) | HCl(aq) (m1) || HCl(aq) (m2) | H2(g) (p2) | Pt

Where the hydrogen gas pressures are p1 and p2 atmospheres respectively and the two hydrochloric acid concentrations are m1 and m2 in mol dm-3. At 25oC calculate or state:

1. an expression for the cell EMF in terms of m1, m2, p1 and p2 (ignoring activity coefficients).
2. The cell EMF when m1 = 0.1M, m2 = 0.2M and p1 = p2 = 1 atm.
3. The cell EMF when the hydrogen pressure p2 is increased to 10atm, all other concentrations remaining the same
4. The cell reaction

As in the previous examples the strategy is first to identify the potential determining equilibria which in this case are:

Right Hand Electrode:                 H+(aq, m2) + e- ⇌ ½ H2(g, p2)

Left Hand Electrode:                H+(aq, m1) + e- ⇌ ½ H2(g, p1)

Formal Cell Reaction:                H+(aq, m2) + ½ H2(g, p1) ⇌ H+(aq, m1) + ½ H2(g, p2)

The Nernst Equation is therefore:

When p1 = p2 = 1, and m1 = 0.1 but m2 = 0.2:

E = (-RT/F) ln (0.1/0.2) = 0.018V

It p2 is changed to 10 atm we have:

E = (-RT/F) ln (0.1x101/2/0.2) = -0.012V

The formal cell reaction in this example was established above. The spontaneous cell reaction – that occurring when the cell is short-circuited – can be seem from the above to depend on the cell concentrations. When p1 = p2 = 1 then the spontaneous reaction is the same as the formal cell reaction since:

ΔG = -0.018F < 0

When p2 is increased to 10 atm, ΔG = +0.012F > 0, so that the direction of the spontaneous cell reaction is reversed.

Solubility Products

Given the standard electrode potentials:

EoAg/Ag+ = +0.799V and EoAg/AgI = -0.152V

Calculate the solubility product, Ksp, and solubility of silver iodide at 25oC.

The first SEP quoted relates to the cell:

Pt | H2(g) (p=1atm) | H+(aq) (a=1) || Ag+(aq) (a=1) | Ag(s)

For which the formal cell reaction is:

Ag+(aq) + ½ H2(g) ⇌ Ag(s) + H+(aq)

ΔGo = -0.799F

Likewise the second SEP is that of the cell:

Pt | H2(g) (p=1atm) | H+(aq) (a=1), I-(aq) (a=1) | AgI | Ag(s)

The potential determining equilibria at the two electrodes are:

RHS:                AgI(s) + e- ⇌ Ag(s) + I-(aq)

LHS:                H+(aq) + e- ⇌ ½ H2(g)

Formal:                AgI(s) + ½ H2(g) ⇌ Ag(s) + I-(aq) + H+(aq)

Which has ΔGo = +0.152F

Subtracting the two reactions gives:

AgI(s) ⇌ Ag+(aq) + I-(aq)

For which:

ΔGo = (+0.152F) – (-0.799F) = 0.951F = -RT ln Ksp

Ksp = 8.5x10-17 mol2 dm-6.

Weak Acids

The EMF of each of the following Harned cells is measured at two temperatures:

Pt | H2(g) (p=1atm) | HCl (10-5M) | AgCl | Ag (E1)

Pt | H2(g) (p=1atm) | HA (10-2M), KA (10-2M), KCl (10-5M) | AgCl | Ag (E2)

Where HA is a weak acid and KA is its potassium salt. The results are as follows:

	293K	303K
E1   / V	0.820	0.806
E2   / V	0.878	0.866

Calculate Ka and ΔHo for the dissociation of the weak acid, pointing out any assumptions you make. Do not ignore activity coefficients, but assume in the second cell that [HA] >> [H+].

We start by identifying the potential determining equilibria in the two cells. In both cases these are:

RHS:                AgCl(s) + e- ⇌ Ag(s) + Cl-(aq)

LHS:                H+(aq) + e- ⇌ ½ H2(g)

Formal:                AgCl(s) + ½ H2(g) ⇌ Ag(s) + Cl-(aq) + H+(aq)

The corresponding Nernst Equation is:

E = Eo – (RT/F) ln [aH+aCl-]

This applies to both cells although the a-values will differ.

Now,

aH+ = γH+[H+] and aCl- = γCl-[Cl-]

Consider the first cell and apply the Nernst Equation at the lower temperature:

0.820 = EoAg/AgCl – (293R/F) ln [ γH+γCl-10-5.10-5 ]

At concentrations as low as 10-5M the solutions are effectively ideal to a high degree of approximation. Physically this arises since the ions are so far apart that the ion-ion interactions are negligible. We can therefore put: γH+ = γCl- ≈ 1, and so deduce that:

EoAg/AgCl = 0.240V (at 293K)

At the higher temperature, but the same method:

EoAg/AgCl = 0.206V (at 303K)

We next turn to the second cell and note that the hydrogen ion activity, aH+, “seen” by the hydrogen electrode will be governed by the dissociation of the weak acid,

HA(aq) ⇌ H+(aq) + A-(aq)

For which we can write the acid dissociation constant:

Now HA is uncharged so that we can safely assume γHA ≈ 1 is a very good approximation.

However, the ionic strength, I, of the solution is in excess of 10-2 mol dm-3 so we expect that γCl- < 1 and γA- < 1.

Returning to the Nernst Equation:

E2 = EoAg/AgCl – (RT/F) ln [aH+γCl-10-5]

At the lower temperature of 293K:

0.878 = 0.240 – 0.058 log [aH+γCl-10-5]

So that:

log [aH+γCl-] = -6.00 (at 293K)

At the higher temperature,

log [aH+γCl-] = -6.00 (at 303K)

it follows that at both temperatures:

aH+γCl- = 10-6

Now,

Ka = aH+aCl-(γA-/γCl-)([A-]/[HA])

= 10-6(γA-/γCl-)(10-2/10-2) = 10-6M

(if γA- = γCl-)

The last assumption is a good one since the Debye-Huckel Limiting Law predicts the same value for the activity coefficients of ions with the same charge experiencing the same ionic strength.

We have shown that Ka has the same value at both 293 and 303K. We can find ΔH for the acid dissociation by using the Van’t Hoff Ischore:

d ln K / dT = ΔHo/RT2

Which shows that ΔHo ≈ 0.

Thermodynamic Quantities

The EMF of the cell

Ag | AgCl | HCl (10-5M) | Hg2Cl2 | Hg

is 0.0421V at 288K and 0.0489V at 308K. Use this information to calculate the enthalpy, free energy and entropy changes that accompany the cell reaction at 298K.

The potential determining equilibria at the electrodes are:

RHS:                ½ Hg2Cl2(s) + e- ⇌ Hg(l) + Cl-(aq)

LHS:                AgCl(s) + e- ⇌ Ag(s) + Cl-(aq)

Formal:                ½ Hg2Cl2(s) + Ag(s) ⇌ Hg(l) + AgCl(s)

ΔGo = - FEo

So,

ΔGo288 = -0.421F = -4.062 kj mol-1 at 288K.

While

ΔGo308 = -0.0489F = -4.719 kJ mol-1 at 308K

Linearly interpolating between 288K and 308K we find:

ΔGo298 = -4.390 kJ mol-1 at 298K

Note that the reaction involves the pure solid metal chlorides and pure elements in their standard states so that the free energies evaluated above are standard free energies, regardless of the concentration of HCl in the cell – the latter does not enter the net formal cell reaction, or influence the cell EMF. It does however play the vital role of establishing the potentials on the two electrodes through the potential determining equilibria given above.

The entropy change be found from:

ΔSo298 = F

= F [ (-0.0489 – 0.0421)/20 ]

= 32.8 J K-1 mol-1 at 298K

The enthalpy change may be readily estimated from ΔHo = ΔGo + T ΔSo

ΔHo298 = -4.390 + [298x32.8/103] = +5.387kJ mol-1 at 298K.

It is apparent that the cell reaction is thermodynamically downhill, but that it is entropy drive, the process being enthalpically unfavourable (ΔH > 0). The positive ΔS value reflects the increase in disorder in converting the solids Hg2Cl2 and Ag into solid AgCl and liquid Hg.