COORDINATION CHEMISTRY NOTES

Hard Soft Acid Base Principle

The earliest evidence of this concept is the Irving-Williams Series of stability of metal complexes. This states simply that for a given ligand, stability of the +2 ion is in the order:

Ba²⁺ < Sr²⁺ < Ca²⁺ < Mg²⁺ < Mn²⁺ < Fe²⁺ < Co²⁺ < Ni²⁺ < Cu²⁺ > Zn²⁺

This is essentially due to decreasing size, and in the case of the Transition Metals, also Ligand Field effects.

It is also noted that certain ligands prefer certain metals, for example Al³⁺, Ti⁴⁺ and Co³⁺ favour one type of ligand while Ag⁺4+>, Hg²⁺ and Pt^2_ another. These were then classified as type-a or type-b. Type-a was largely the metal ions of Group 1,2 + lighter Transition Metals in high Oxidation States, + H⁺. Type-b were the heavier Transition Metals and lower Oxidation State metals. Ligands can also then be classified based on their preference for a or b.

Tendency for a	Tendency for b
N >> P > As > Sb	N << P > As > Sb
O >> S > Se > Te	O << S < Se = Te
F > Cl > Br > I	F < Cl < Br < I

These were later classed Hard (a) and Soft (b). Thus a Hard Acid is a type-a metal ion, while a Hard Base is e.g. NH₃ or F^-, while a Soft Acid is a type-b metal ion, and a Soft Base is e.g. phosphine, iodide.

• Hard - tend to be small, slightly polarisable
• Soft - tend to be larger, more polarisable

Pearson Principle for predicting stability: Hard Acids prefer to bind to Hard Bases, and Soft Acids prefer to bind to Soft Bases. It should be noted though that this is a simple rule, and not an explanation. Thus any acid/base can be classed as hard or soft based on its preference for hard or soft reactants. For example,

BH⁺ + CH₃Hg⁺ ⇔ CH₃HgB⁺ + H⁺

H⁺ is the hard acid, Hg⁺+> the soft acid. For a Hard Base B, the reaction goes to the left, while for a Soft Base B the reaction goes to the right. However the borderline between hard and soft is relative, and so there is no sharp divide. For example, all alkali metals are "hard", but Cs⁺ is significantly softer than Li⁺. Similarly R substituents on the ligands greatly influence the hardness/softness, e.g. for PR₃ when R is electron-withdrawing the softness is reduced. Borderline acids are typically 1^st row Transition Metals from Iron to Zinc, Pb²⁺, NO⁺, while bases are typically Br^-, N₂, SO₃^2-. There are plenty of others.

Limitations of HSAB Principle:

• Hardness and softness has to do with competition and says nothing about the strength of a donor or acceptor (see below).
• The HSAB Principle is descriptive, not explanatory. Generally it is assumed that hard-hard interactions are more electrostatic in nature (involving smaller, more highly charged ions, and/or more polar molecules) and that HOMO/LUMO overlap is more important in soft-soft interactions. Thus soft donors should have a relatively high HOMO and soft acceptors a relatively low LUMO, so that efficient mixing can occur.
• However, other factors may be involved. Soft-soft interactions may have a significant contribution from dispersion forces between polarisable atoms. In some cases, π- backbonding may also be important.

It is important to make the distinction between Hardness and Softness and Acid/Base Strength. Hardness/Softness has already been defined as the special stability of hard- hard and soft-soft interactions, but Acid Base Strength must also be defined.

Acid Base Strength measures the inherent acidity/basicity of a given acid or base. Measurement requires non-competing solvent effects and therefore is best done in the gas phase.

The inherent basicity is the base’s proton affinity, and this is the energy released from the reaction: B + H⁺ → BH⁺. This can be measured using Born-Haber cycles, and the largest known to date is that for N^3-.

The inherent acidity is thus proton loss, that is HF → H⁺ + F^-. The more endothermic this reaction is, the weaker the acid. For Lewis Acids, proton’s must be disregarded and the obvious quantity to use instead is electron affinity (same value). Thus a large electron affinity means a strong acid. The E_A of a monopositive cation is equal to the E_I of the metal atom. Thus it makes sense that Group 1 & 2 metals are weak Lewis Acids, while the Transition Metals are stronger.

The measurement of acid base strength can be converted to solution chemistry by instead considering the enthalpies, as -∆H_f = E_AE_B + C_AC_B. E corresponds to the susceptibility of the acid/base to electrostatic forces, while C to the susceptibility to covalency. Thus electrostatic acid & base is stable, while a covalent acid & base also form stable. This allows for the prediction of those complexes not measurable. It also usefully contrasts ionic and covalent tendencies for acids and bases.

This simple estimation was later modified to include a -W term, which was R_AT_B and measures the charge transfer occurring as well (receptance / transferance). This takes into account the variation of H⁺ acid strength in solution / gas phase. As a gas, H⁺ accepts a great amount of electron density, while solvated H⁺ is expended this energy already and so the transfer energy is lowered.

With these definitions considered, we can look now at the distinction between Hard/Soft and Strength. A good example are the bases ^-OH and F^-. They are both hard and form stable complexes with hard acids, but the hydroxyl is 10¹³ times as basic.

The key concept here is that stronger softer bases can displace weaker harder bases from a hard acid like H⁺, i.e. strengths of base forces reaction in spite of hard-hard considerations. The trend of the Irving-Williams series shows this well, as it is essentially a measure of increasing acidity of M²⁺ and superimposed upon this is a hard-soft factor. The hard-hard factor only tends to be favoured for acids/bases closely related in strength, and is just a general trend due to the extra stability it confers.

As such, it is important to consider how this extra stability comes about.

The theoretical basis for the hard-hard interaction is taken primarily from an electrostatic viewpoint. Typical hard acids/bases such as Li⁺ and F^- are all typically classed as ionic compounds, so this is valid. The electrostatic (or Madelung) Energy of an ion pair is inversely proportional to the interatomic distance, so smaller ions have greater attractions. Thus, hard-hard favours small ions such as Li⁺ and F^-.

The electrostatic argument cannot be used for soft-soft interactions as the Madelung Energy would be weak. Thus, it can be extrapolated as a covalent factor, so polarizing power and polarizability of the electrons becomes important. Thus soft transition metal acids with dn electrons where n >= 6 show soft-soft interactions (particularly d¹⁰). The polarisation effects here resemble Fajans’ ideas.

Fajans’ Rules - originally came about to consider partial covalent character in ionic compounds. They consider the effect of a small highly charged cation on an anion. A large soft anion means the cation polarises it. The extreme of this is the cation penetrates the anion’s electron cloud to share electrons in a covalent bond. There are 3 rules to estimate the extent of polarisation:

1. Polarisation increases due to high charge / small size of cation. This brings about the ionic potential of the cation, φ = ^Z/_r. Interestingly this property illustrates the diagonal relationship of Periodicity well.
2. Polarisation increases due to high charge / large size of anion. Polarisability is related to softness as softness depends on how deformable the electron-cloud is (which in turn depends on size).
3. Polarisation depends on electron configuration of the cation. The ionic potential results from total positive charge of the cation, which depends on the degree of shielding of the electrons present. Ionic charge alone as considered in (1) would mean perfect shielding was present, and it is known that this is not the case, particularly for Transition Metals were d-electrons shield poorly. Hence, they favour softness.

Electronegativity is another property that is considered when looking at the basis of hard/soft acid/base. High electronegativity usually corresponds to hardness. It is important here to remember to consider the ion in question, not the atom. For example, Li has low electronegativity, but Li⁺ is very high due to a very large second ionisation energy. Transition Metals on the other hand have low electronegativity due to variable oxidation states (although in high oxidation states it will increase in value). They are thus soft when in low oxidation states.

The combination of factors above give rise to the Hard-Soft Acid-Base (HSAB) Theory. Attention was then given to the frontier orbitals (HOMO and LUMO) in order to better develop the understanding of the bonding involved.

Using Koopmans Theorem: Energy of the HOMO corresponds to the Ionisation Energy, and the Energy of the LUMO corresponds to the electronegativity and HSAB, it was realised that a Hard acid or base must have a large HOMO-LUMO gap, while the gap for Soft was smaller.

Presence of low-lying unoccupied Molecular Orbitals capable of mixing with the ground state accounts for the polarisability of soft atoms. The consequence of polarisability was distortion of the electron cloud occurring to reduce repulsions and enhanced σ-donation and π-backbonding. Thus soft acid/bases better at π-bonding. Note that longer σ/π bonds are not as strong, hence Se, As, Te, Sb are not as soft as S, P. This is because they need overlap. This is also why CO is so good, being small.

Bonding of Nitric Oxide

NO contains unpaired electron, and bonding to metal involves:

• Donation of the electron to the metal - bonds as NO⁺ cf. CO
• Donation of electron from metal to NO - bonds as NO^-
• With additional electrons, N rehybridises to sp² with lone pair and M-NO bent
• Formation has implications for metal oxidation state (difference of 2)
• Bonding type difficult to assign by IR although v(NO) lower for bent form - considerable overlap of regions
• MO theory overcomes formalism problems
• Levels obtained for metal-NO complex and NO and metal electrons fed in. If HOMO π-bonding wrt N-O, then linear
• If more electrons added to antibonding orbitals, N-O bond weakens, lower energy when bent (Walsh Diagram)
• Analogues of M-NO, M-NS also known

Other M-N bonded ligands show electronic behaviour.

If NO bends then metal can accommodate additional 2 electron donor ligand. The 18 Electron Rule can be used to rationalise the geometry for coordinated NO and related ligands.

Common Coordination Geometries

Octahedral:

The most common geometry for transition metal complexes.

• But frequently distorted - steric effects, ligand constraints and electron configuration of metal, e.g. Jahn-Teller for Cu(II)
• For kinetically inert complexes, e.g. Co(III) possibility of isomers

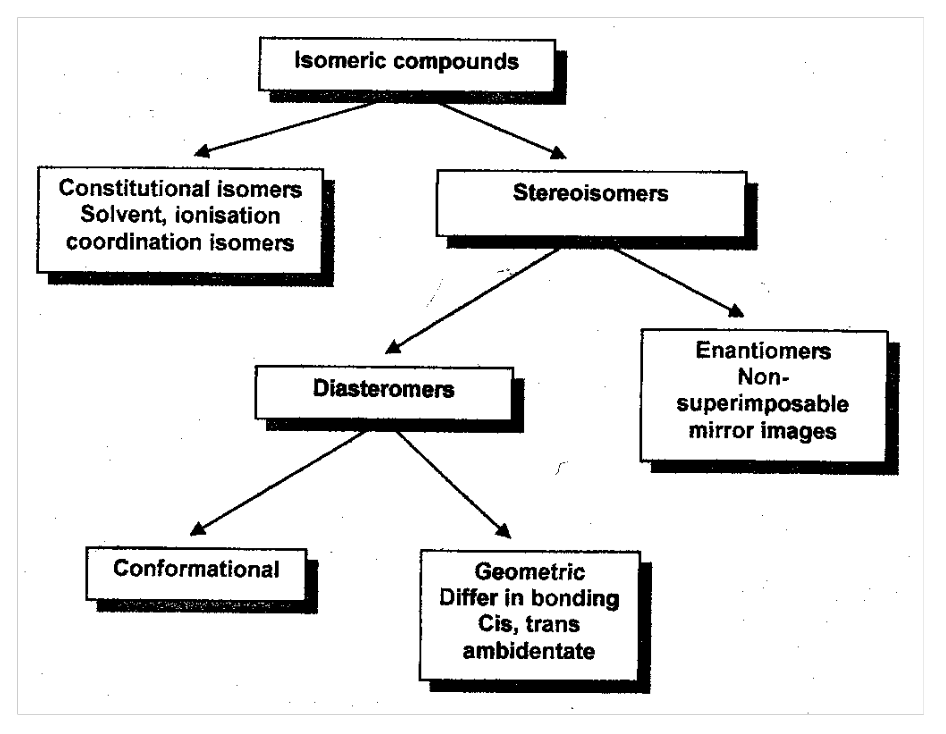
Enantiomers and Diastereomers

Complexes of the type ML₄L₂ exist as cis or trans isomers. Trans [CoCl₂(en)₂]⁺ shown:

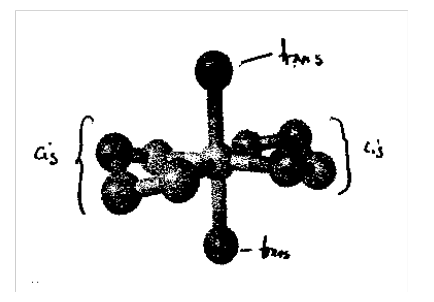
Trans green, cis violet. [Co(NH₃)₃(NO₂)₃] - fac and mer isomers, fac shown:

[Co(en)₃]³⁺ looking down threefold axis - enantiomeric (left).

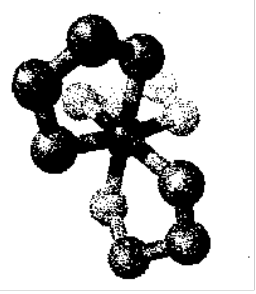
Note that the molecule Mabcdef (i.e. 6 different ligands around M) has 30 stereoisomers and 15 enantiomeric pairs!

Enantiomers are also found for Mabc₂d₂, Mabcd3 and Mabcde₂.

Separation of optical isomers by chromatography using chiral column.

For cations separate using optically active tartrate anion, fractional crystallisation.

Anions resolved using brucine or other optically active cations.

Absolute configurations by X-ray crystallography.

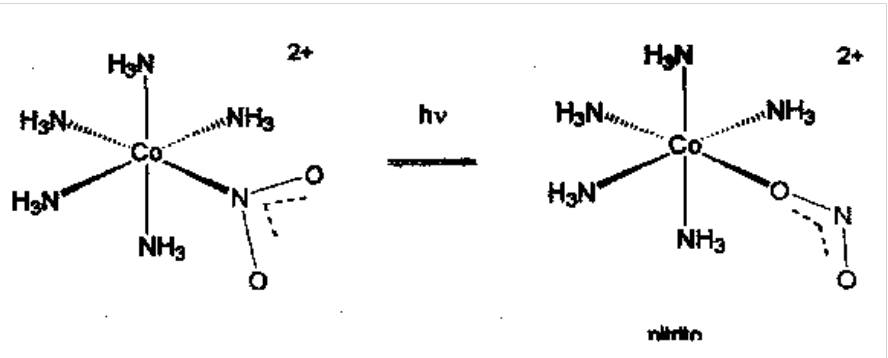
Ambidentate Ligands - two isomers possible for nitrite when coordinated:

Constitutional Isomerism

Hydrate Isomerism

Three different forms for CoCl₃.6H₂O.

[Cr(H2O)6]Cl3	violet
[CrCl(H2O)6]Cl2.H2O	blue-green
[CrCl2(H2O)6]Cl.2H2O	green

Ionisation Isomerism

Different anionic ligands bound.

[Co(NH3)5SO4]NO3

[CO(NH3)5NO3]SO4

Coordination Isomerism

Ligand to metal ratio remains constant, but metal-ligand combinations change. Three compounds with empirical formula PtCl₂(NH₃)₂ -

[PtCl2(NH3)2]
[PtCl(NH3)3][PtCl3(NH3)]
[Pt(NH3)4][PtCl4]	Magnus green salt

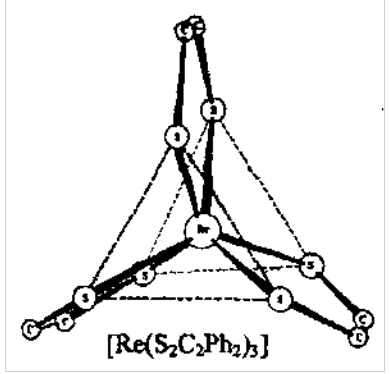
Trigonal Prismatic Geometry:

Some 6 coordinate complexes, especially with dithiolene S ligands, have alternative trigonal prismatic geometry.

S-S interactions play a role in stabilisation, but d-electron population also important.

Dithiolenes are examples of “suspect” ligands - can be viewed as neutral or 2-ligands.

WMe₆ is another example.

Square Planar Geometry:

Tetrahedral geometry most common for 4 coordination. Can be distorted for same reasons as octahedral.

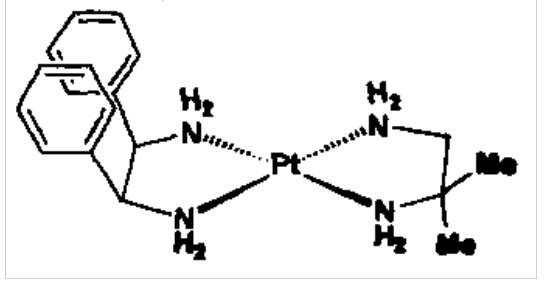
Square planar geometry is favoured by many d8 complexes, e.g. Rh(I), Pt(II), Au(III).

Can have optical and geometric isomers.

Diamine complex on the right is enantiomeric:

Other Geometries:

Factors affecting shape:

• Repulsion between atoms and bonds - steric and packing effects
• Electron-configuration of atoms / ions
• Other electronic factors, e.g. trans effect

Five Coordination

Trigonal Bipyramidal and Square Based Pyramidal. The energy difference between the two forms is often small.

The latter often has multiply bonded ligand in the axial site, with high trans effect.

Seven Coordination

Capped trigonal prism (e.g. [NbF₇]^2-, or pentagonal bipyramidal (e.g. [UO₂(H₂O)₅]²⁺). The latter is most common.

Eight Coordination

e.g. [Zr(oxalate)₄]^4-. Square antiprismatic structure. Favoured by bidentate ligands with small bite angles and small charged ligands with larger early TMs.

Nine Coordination

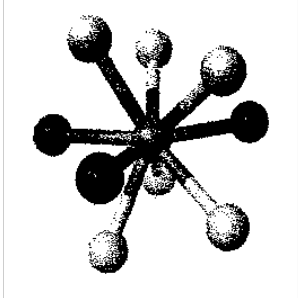
Found for [ReH₉]^2-

Tricapped trigonal prism.

Also for lanthanides with bidentate ligands with small bite angles.

Two and Three Coordination

Many compounds that appear to have low coordination such as CoCl₂ are in fact polymeric with halide bridges (or the structure can be viewed using a close packing model).

Two Coordination is common for d¹⁰:

• Shielding by inner d and f orbitals - poor, and high Z_eff → d-orbitals high in energy, and high s-p energy difference disfavours s-p hybridisation. LINEAR coordination using d-s hybrids
• Large numbers of anionic ligands cannot be accommodated due to small ionic charges
• Achieved for other metals by extreme steric crowding

Three Coordination is often of the trigonal planar geometry. Groups 11 and 12 again favour low coordination, and 3 coordinate complexes are known for Cu and Au, e.g. [Au(PPh₃)₃]⁺.

Also, steric crowding can lead to this coordination number, e.g. in complexes of the type [M{N(SiMe₃)₂}₃].

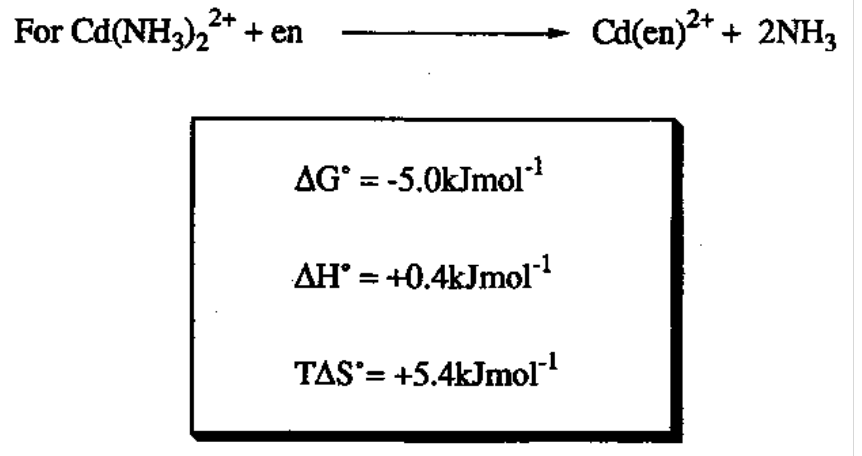
Complex Stability

[M(H₂O)₄]ⁿ⁺ + 4L ⇔ [ML₄]ⁿ⁺ + 4H₂O

Overall stability constant,

β_n = [ML_n]/[M][L_n]

Stability Constant implies the strength of species as ligands relative to the strength of H₂O.

K₁ > K₂ > K₃ > … > K_n

This can be explained statistically, as:

ML₆ + L’ ⇔ ML’L₅ + L

ML₄L’₂ + L’ ⇔ ML₃L’₃ OR ML₄L’₂

Depending on which is displaced, i.e. fewer ligands available for displacement with each step.

Also, thermodynamically, entropy causes the decrease as free ligands are immobilised.

Steric factors - L’ may be bigger than L.

Any deviation from that trend is usually the result of a major change in the electronic structure of the complex, e.g. change of geometry.

Some anomalies

Copper(II) - Ammonia. Consequences on K5 and K6 of the Jahn-Teller effect - unusually weak bonding at the 5th and 6th coordination positions. Hence, Cu(NH₃)₆²⁺ can only be obtained in liquid ammonia

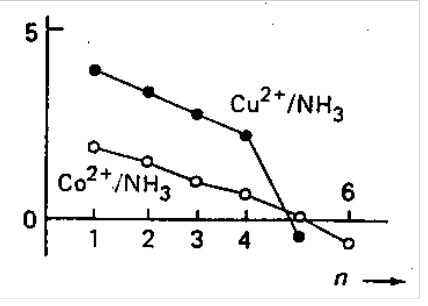
Cadmium(II) Iodide. Stereochemical change from CdI₂(OH₂)₄ (octahedral) to CdI₃(OH₂)^- (tetrahedral). This causes release of additional water molecules.

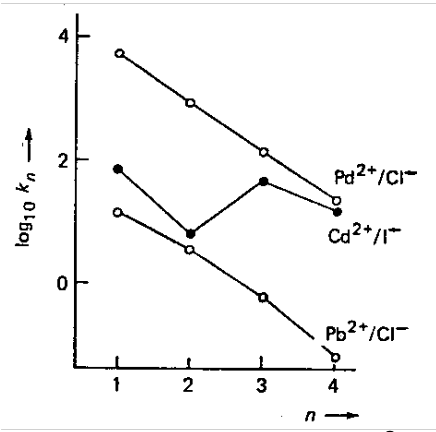
Similarly, stepwise stability constants for Cd²⁺ with Br^- would be expected to decrease from K₁ to K₂ to K₃ to K₄. However, there is an increase from K₃ to K₄. This is because of adoption of the tetrahedral [CdBr₄]^2- as water ligands are ejected from [CdBr₃(OH₂)₃]^- (entropy driven).

Iron(II)-1,10-phenanthroline. Magnetism change: [Fe(phen)₂]²⁺ is high spin, while [Fe(phen)₃]²⁺ is low spin.

Similarly, for Fe²⁺ and bipy, moving from K₂ to K₃ sees a large increase as [Fe(bipy)₂(OH₂)₂]²⁺ forms [Fe(bipy)₃]²⁺. The key change here is not structural, but a change from t_2g⁴e_g² (high spin) to t_2g⁶ (low spin), and a gain in CFSE. Presumably the 3 bipy ligands is sufficient to stabilise the low spin form, but 2 is not.

Crystal Field Effects on Stability Constants

Metal	V2+	Cr2+	Mn2+	Fe2+	Co2+	Ni2+	Cu2+	Zn2+
Config	d3	d4	d5	d6	d7	d8	d9	d10
CFSE	12Dq	6Dq	0	4Dq	8Dq	12Dq	6Dq	0
Log K1 (en)	4.6	5.2	2.7	4.3	5.9	7.6	10.7	5.9
Log K1 (edta)	12.7	12.8	12.3	14.2	16.1	18.5	18.8	16.5

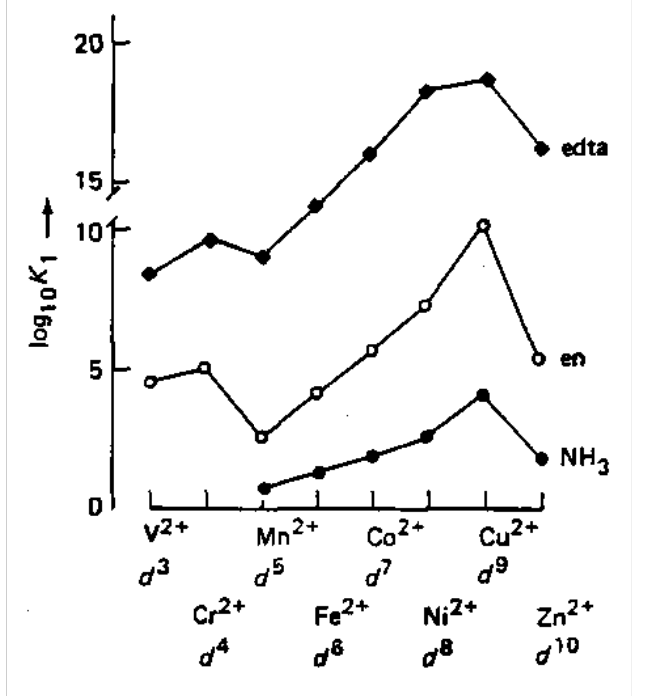
Also see a similar trend in -∆H, i.e. the trend is insensitive to the nature of the ligand. Peaks at Cu²⁺ are due to Jahn-Teller distortions (destabilising). Ligands in the plane are stabilised, while axial often do not bind at all.

Across the period, Z_eff increases, radii decrease, Lewis Acidity increases, and stability as a result increases. This all implies a stronger M-L bond.

This is known as the Irving-Williams Series - the dependence of stability constants and formation enthalpies on d electron configuration for high-spin complexes of first row transition metal 2+ cations.

Smaller r = bigger K_f.

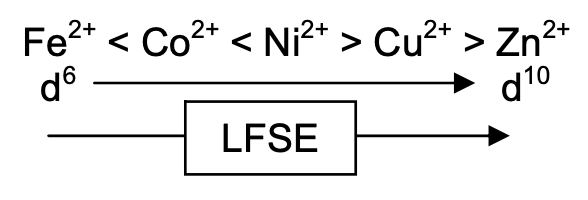
Also, Electronic Factors - ligand binding governed by charge and MOs:

σ-donor - favoured

π-acceptor - favoured

π-donor - unfavoured

High spin / low spin important for d⁶. Low spin stabilises by 12Dq.

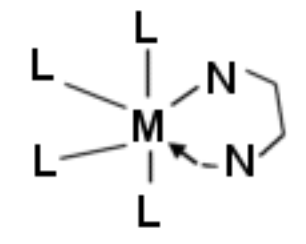
The Chelate and Macrocyclic Effects

Chelate Effect

Enhanced stability of chelate rings as compared to a similar monodentate system. Both entropic and enthalpic contributions:

Entropy driven as more free molecules in solution as each ligand displaces 2.

Localised concentrations can also favour:

The other N is now nearby to M despite many solvent molecules - intramolecular faster. Relatively, it is highly concentrated.

Hence, we can expect ring size to matter. As the ring increases in size, log K decreases, as once one ligand point is bound, the second is less likely to attach when the chain is longer (further away). They are however notable exceptions seen with 5 and 6 membered chelate rings.

Enthalpy is also favourable because generally polar groups are brought together - part of mutual dipolar repulsions are overcome in forming a ligand.

The chelate effect is also magnified when there are multiple chelating rings, e.g. in EDTA^4-.

When relating these to different metals, we must consider the concept of “bite size” of the chelating ligand. In general, this is larger for 5 membered rings than 6, so then 6- membered favours larger metal ions. Also, the bond angle for 5 membered rings (N-M- N) is smaller, so a small metal ion can get closer to the smaller ring.

Macrocyclic Effect

Macrocyclic ligand complexes are more stable than open chain analogues. Depending on the system, can have favourable ∆S and/or ∆H, although enthalpy generally dominates.

Major contributing factors to favourable ∆H are:

1. Greater basicity of donor atoms due to increased alkylation
2. Macrocyclic ligands are frequently less strongly solvated than acyclic analogues (fewer ligand-solvent bonds to break on complexation)

Overcomes repulsive forces between polar donor groups.

Favourable ∆S results from macrocycles which are less conformationally flexible, i.e. lose fewer degrees of freedom on complexation.

Concept of Preorganisation:

"The more highly hosts and guests are organised for binding and low salvation prior to their complexation, the more stable will be their complex."

e.g. Crown ethers are more preorganised than acyclic ethers, Cryptands are more preorganised than crown ethers.

Generally,

Spherands > cryptands > crown ethers > polands

↓ thermodynamic stability →

↓ degree of preorganisation →

Spherands = ligands that are completely preorganised for complexation during synthesis.

• 6 MeO in an octahedral array. Shielded from salvation by 6 aryl and 6 methyl groups. Solid state structures of ligands + Li⁺ complex are very similar
• Stability constants are highest known for group 1 metal cations
• Amazing selectivity, based on size
• Kinetics of complexation / decomplexation are extremely slow for spherands. Cannot be used in chemical sensors - response time too slow. Used in extractions for purification of M⁺ salts

The Template Effect

Metal Ion Template Reactions

One in which coordination of L to at least one metal ion is necessary, either for the reaction to proceed, or to change product distribution in favour of specific compound, e.g. pthalocyanines.

Schiff-Base Condensations

R₂C=N-R’ formation.

A carbonyl is attacked by an amine, which then loses water.

Metal is coordinated to N.

Control of the reaction is by the size of the template metal-ion used. Small metal cations lead to [1+1] condensations (e.g. Mn²⁺, Fe²⁺). Large metals such as Ba²⁺ give [2+2] macrocyclic products.

Equilibrium Template Effect

Complexation to a metal ion stabilises one component of an equilibrium mixture, shifting the equilibrium to favour formation of the metal complex:

Kinetic Template Effect

Coordination of the reactive groups to a metal ion which holds these groups (template) in the proper geometry to favour a particular macrocycle. Ring closing reaction:

Orientation by metal template favours cyclic product formation.

Freeing ligand is hard. Either:

1. Reduce Imine Linkage
2. Addition of competing ligand

Template reactions leading to macrocyclic ligands - Encapsulation Reactions.

Non-Template Synthesis of Macrocycles

High dilution conditions. Simultaneous drop-wise addition of reactants A + B to a vigorously stirred large volume solvent over hours/days. Always a low concentration of reactants → cyclisation rather than polymerisation.