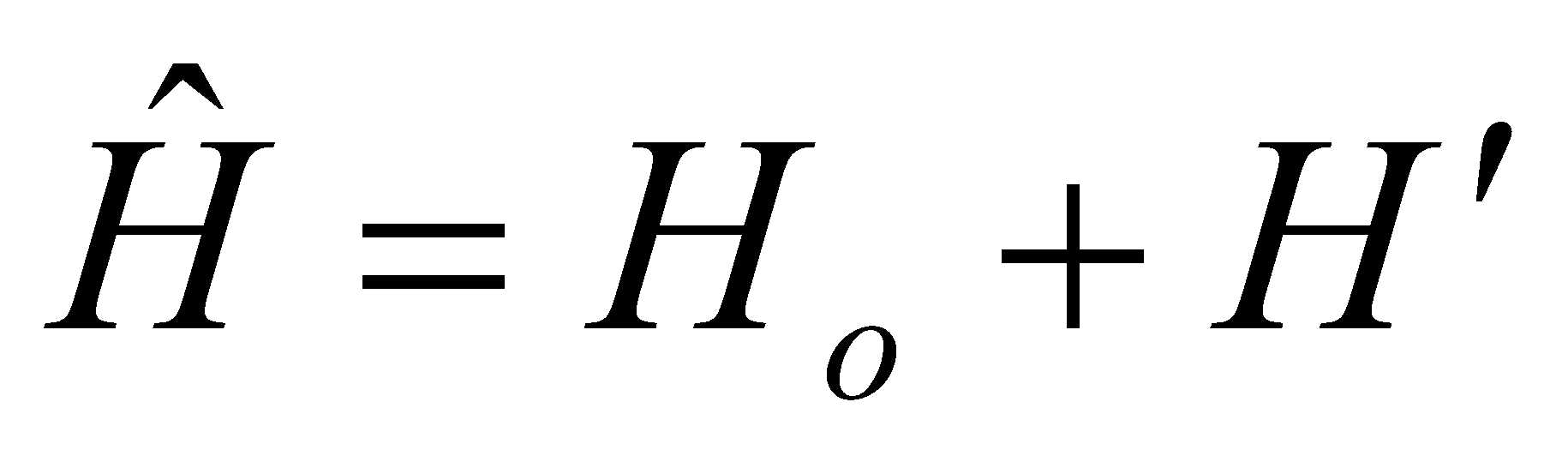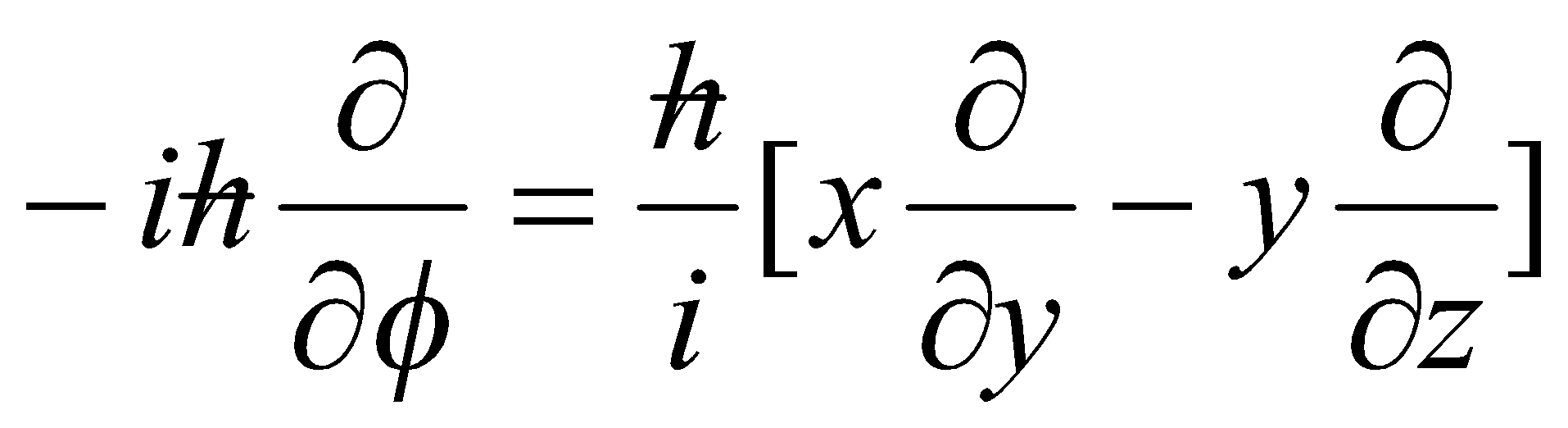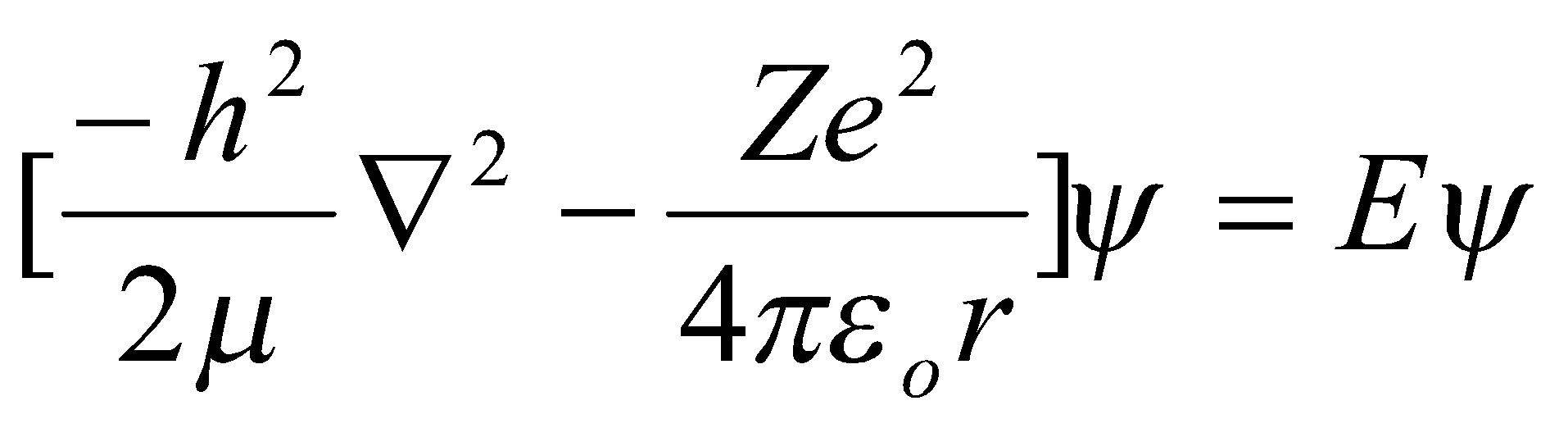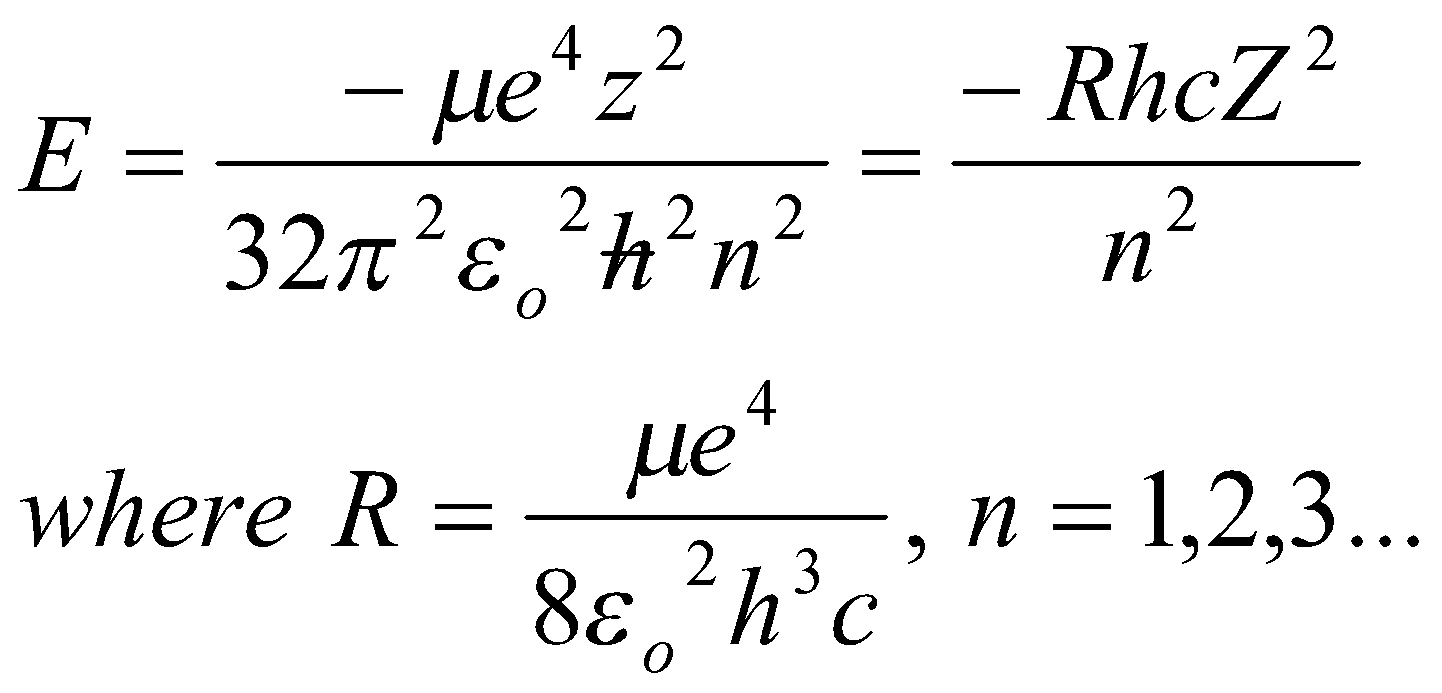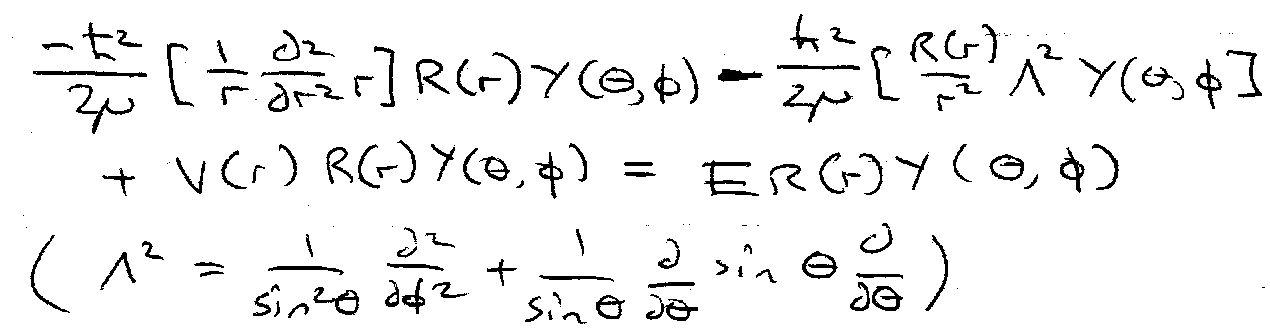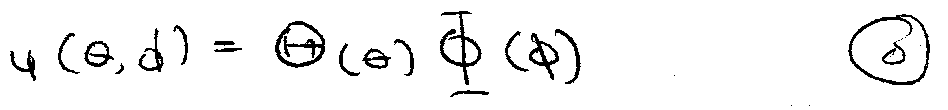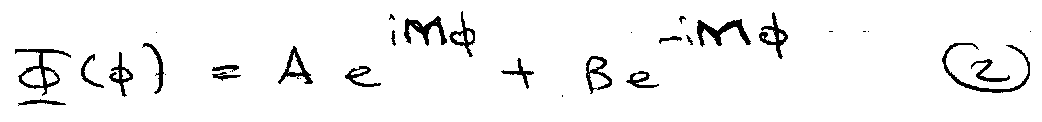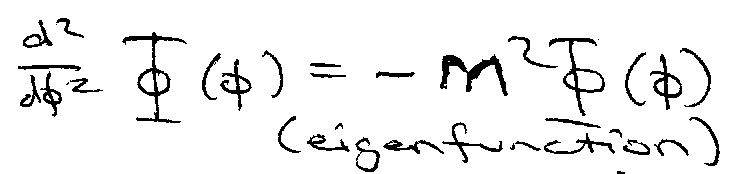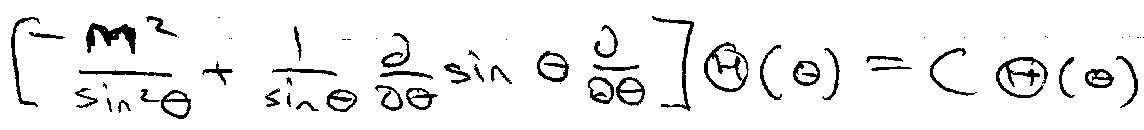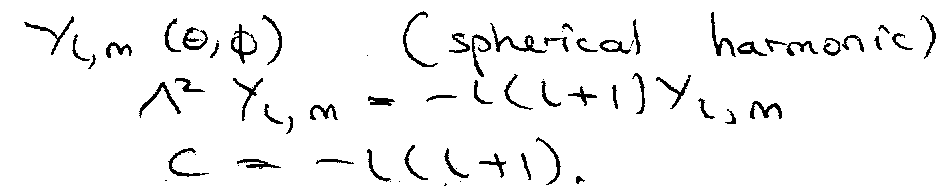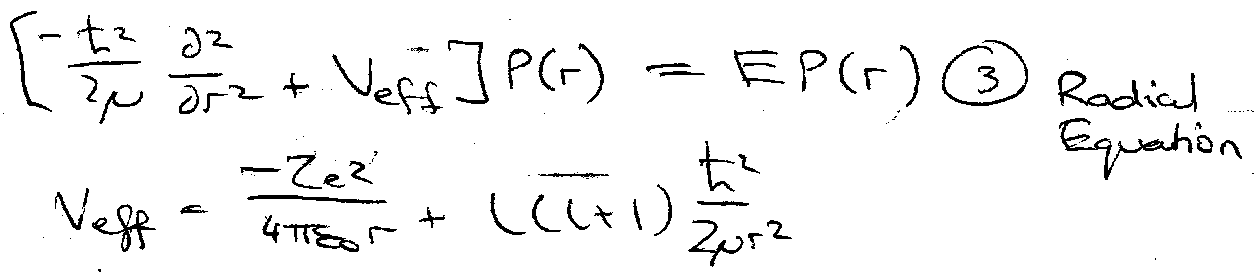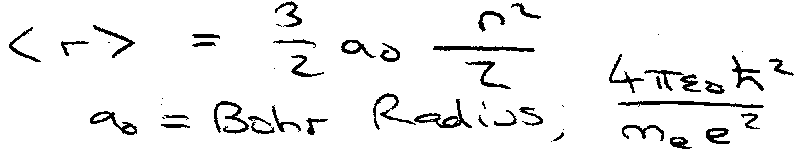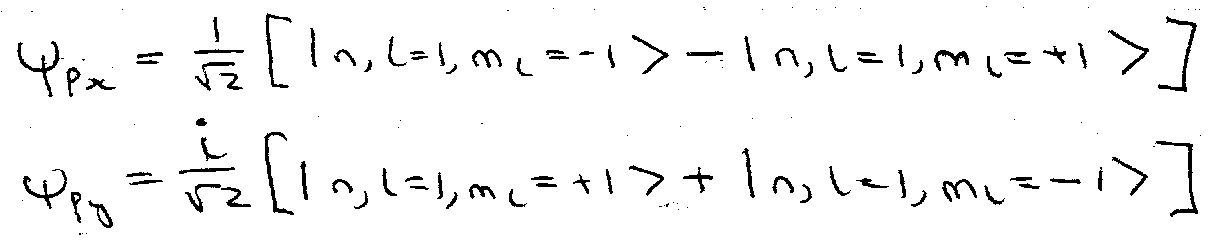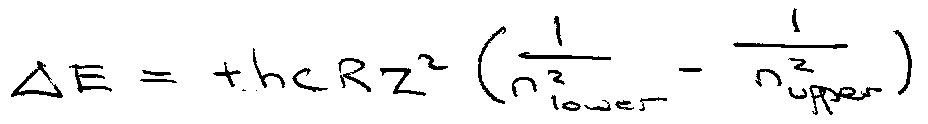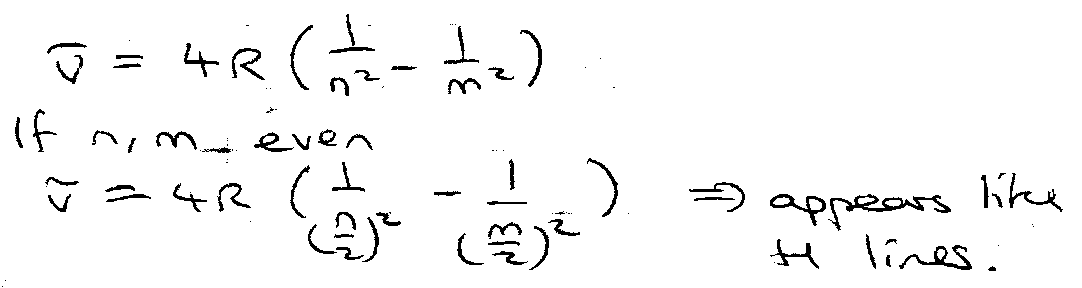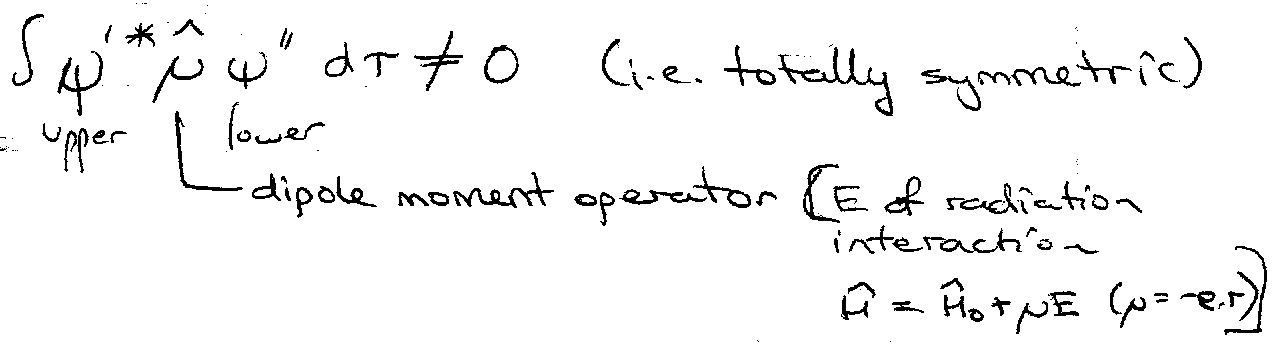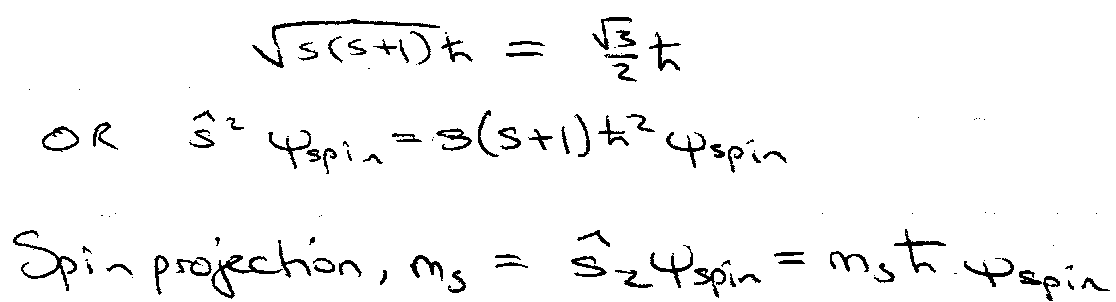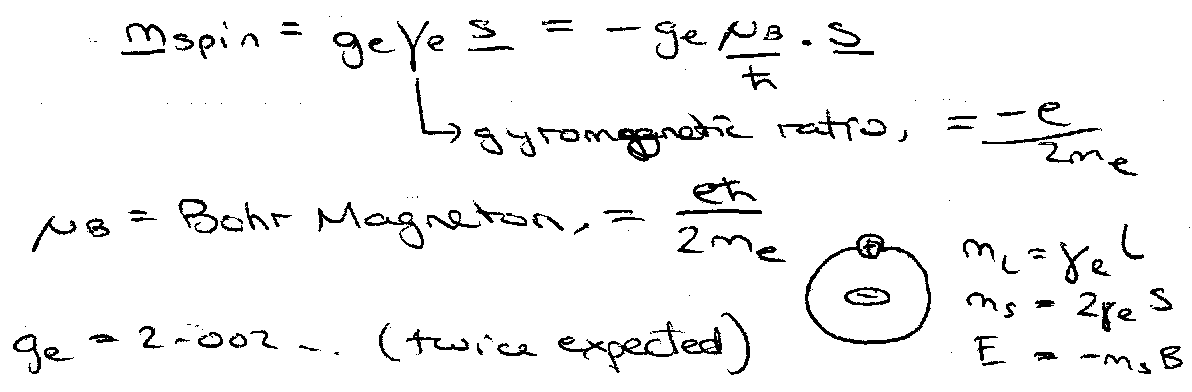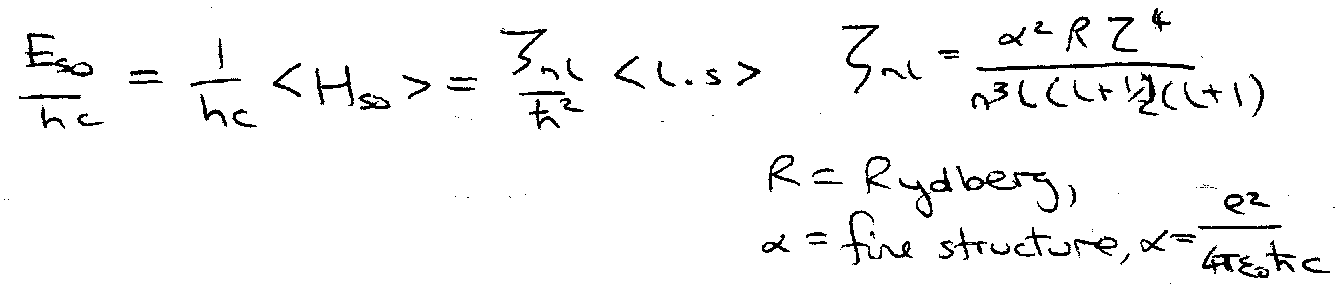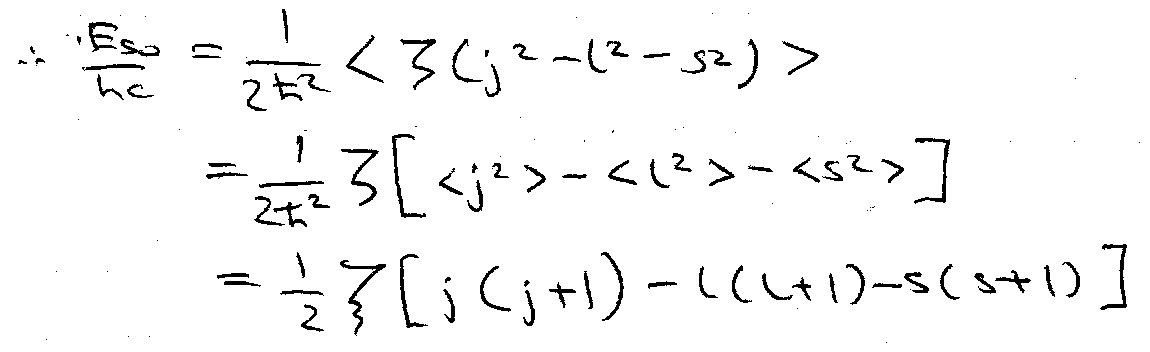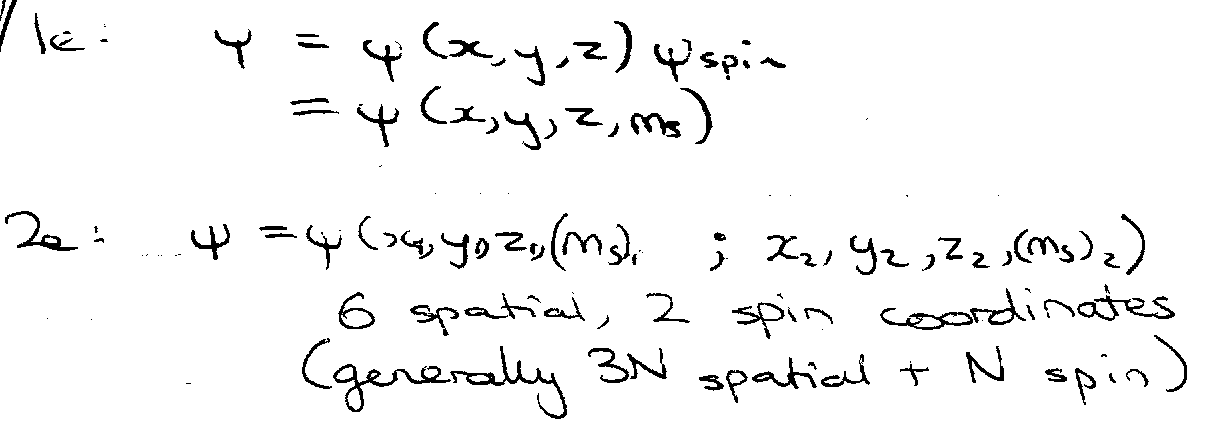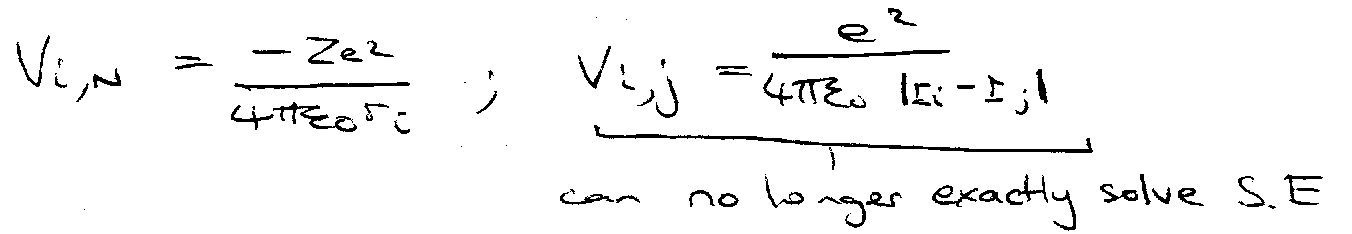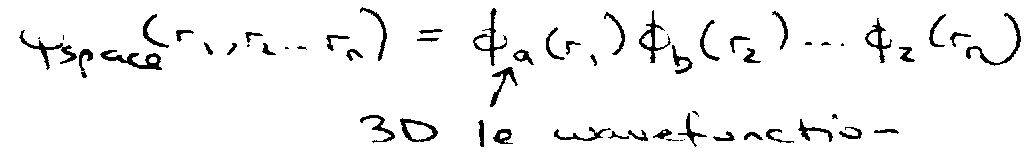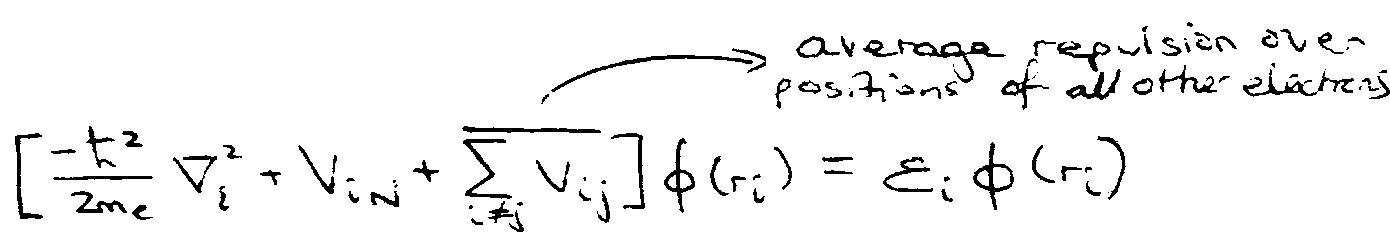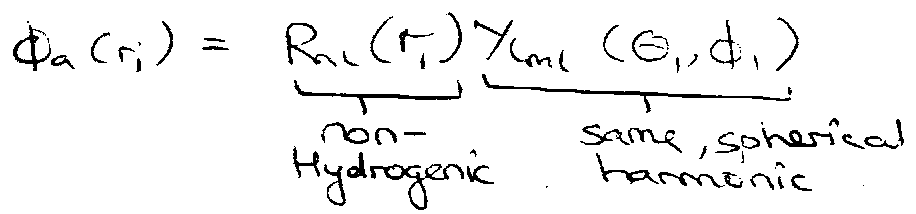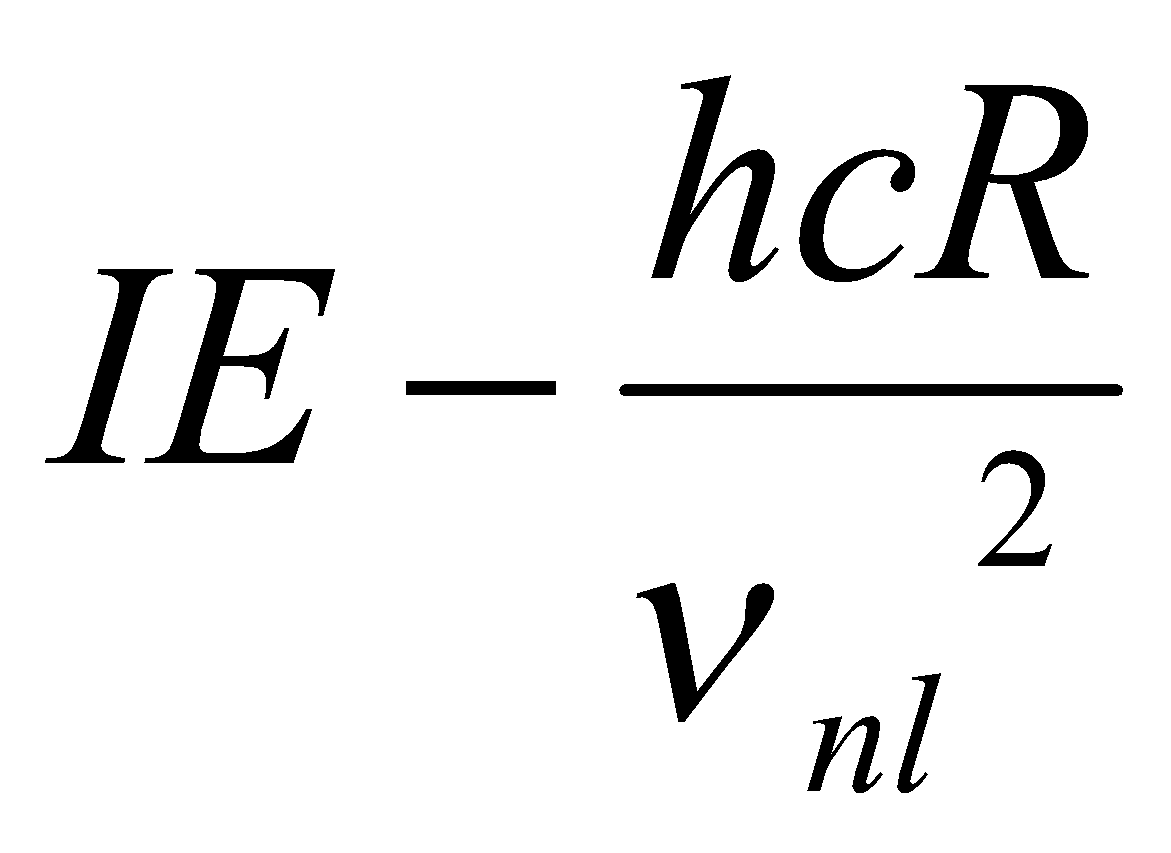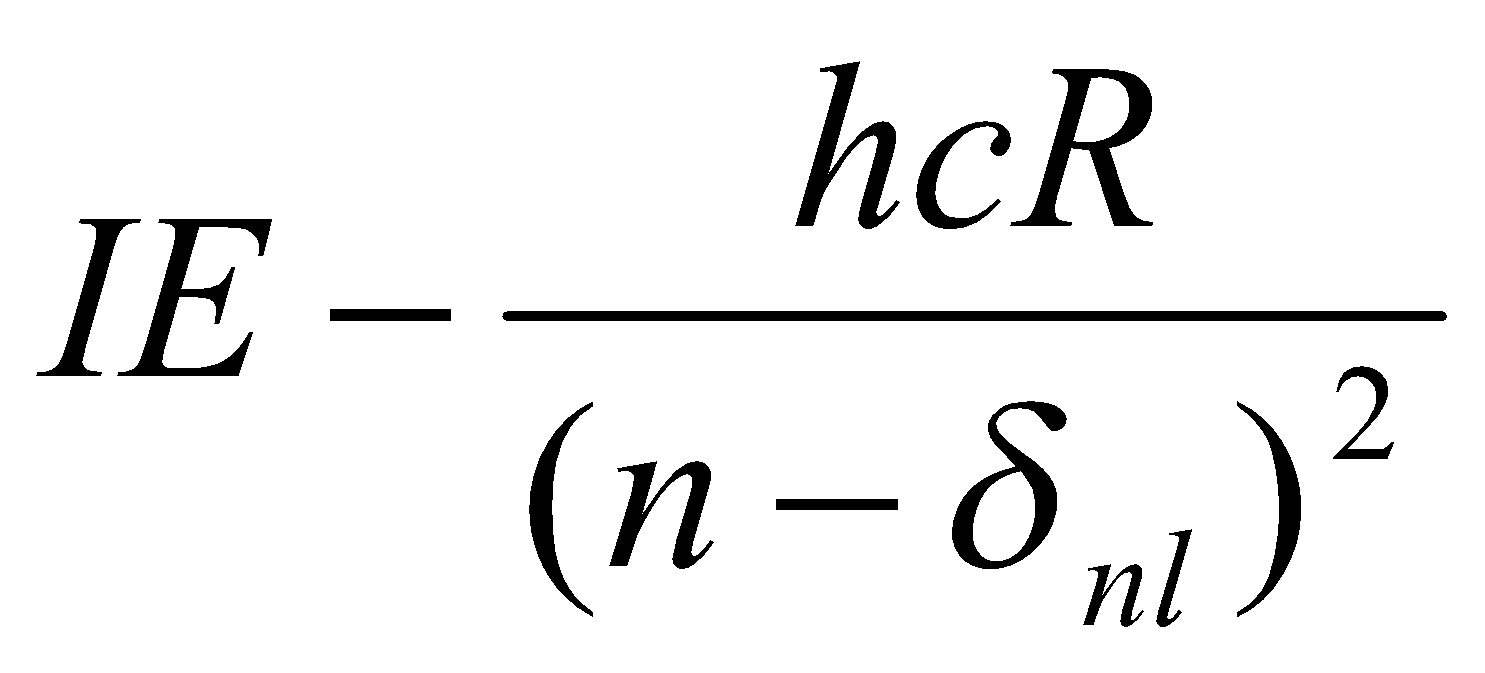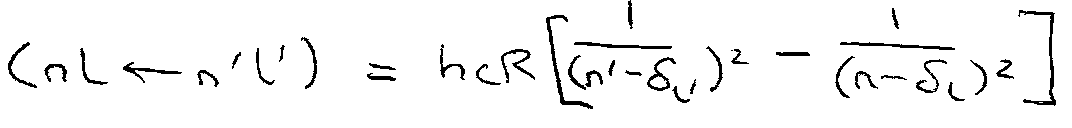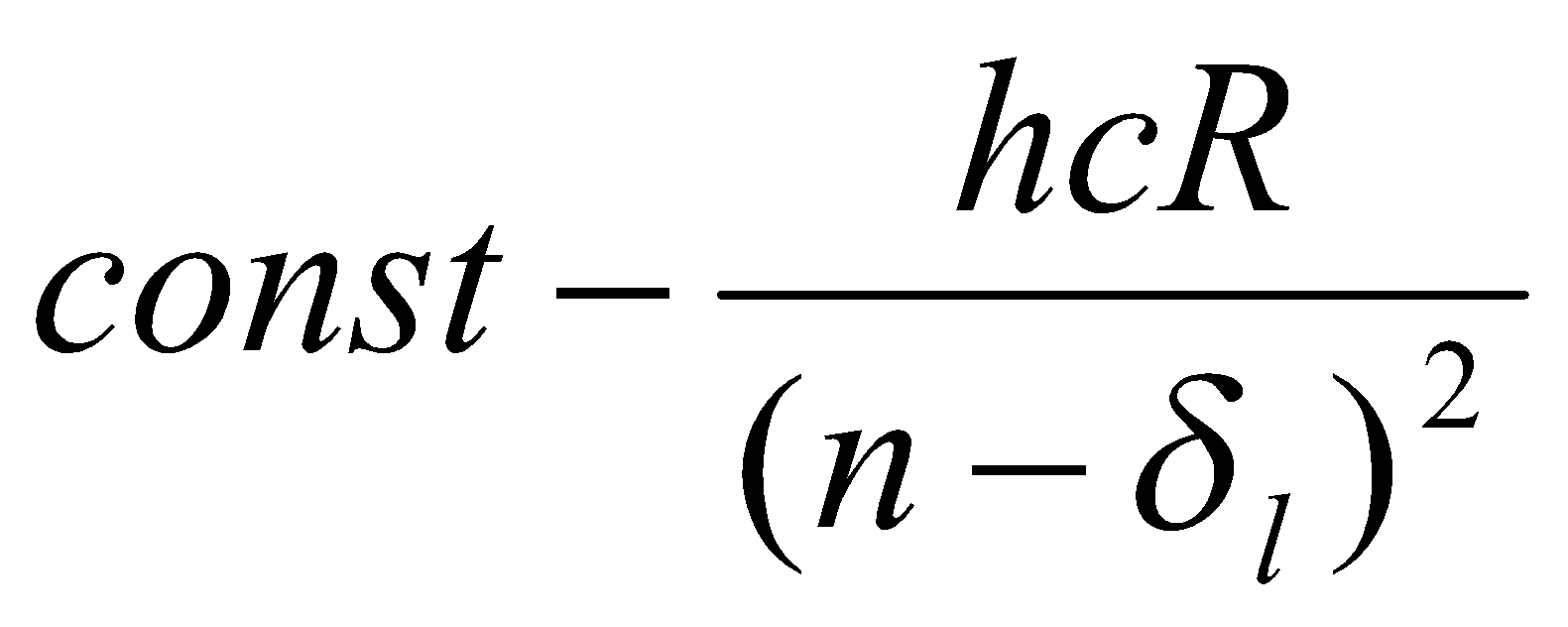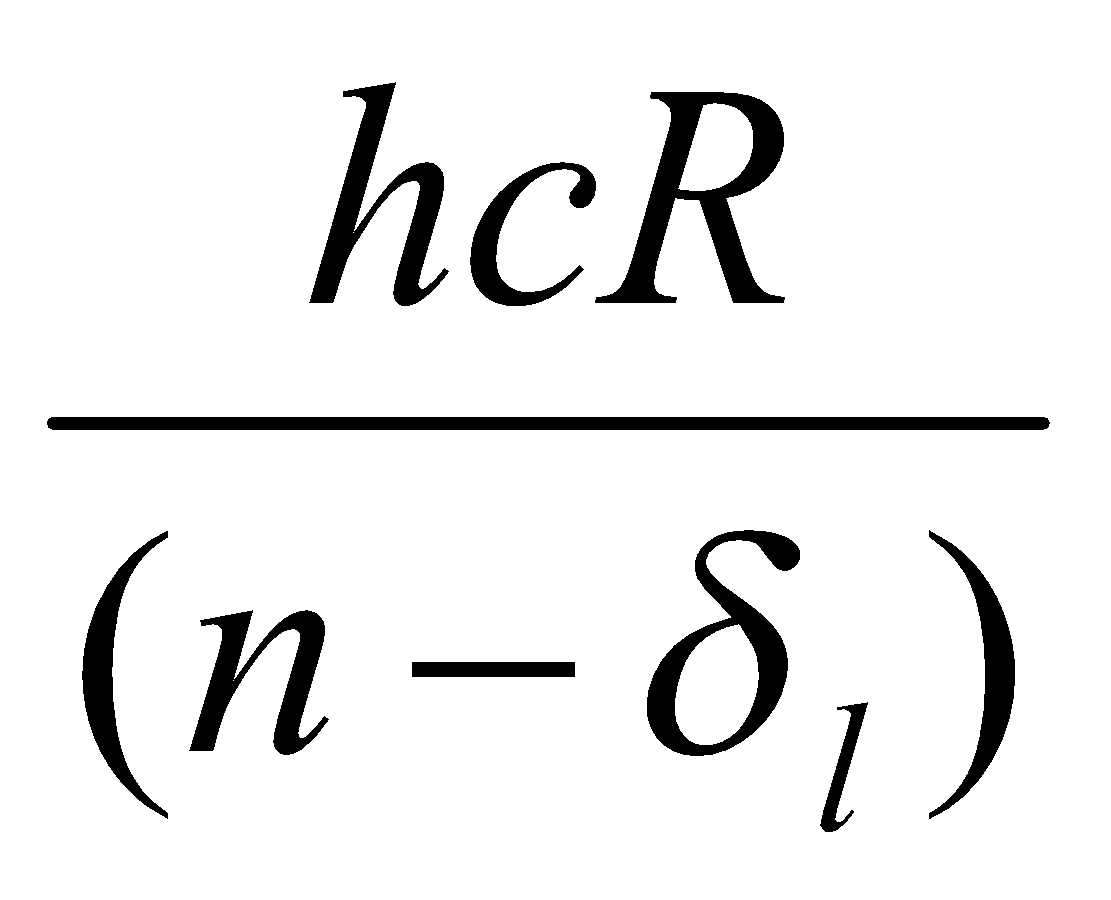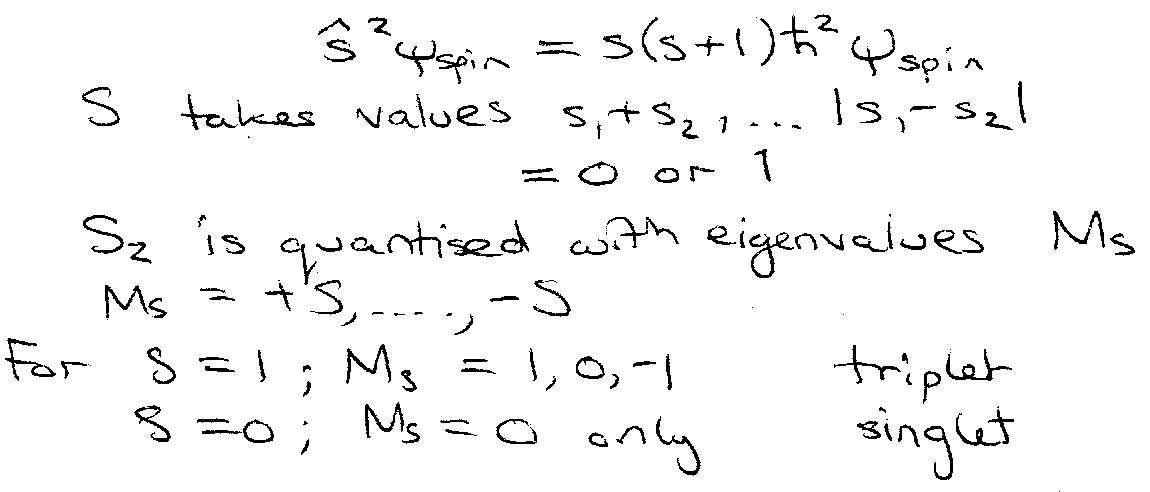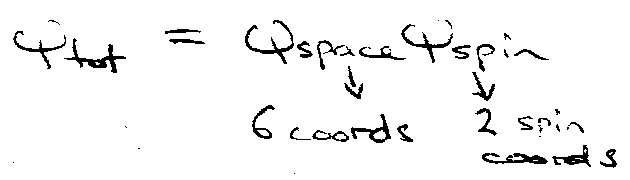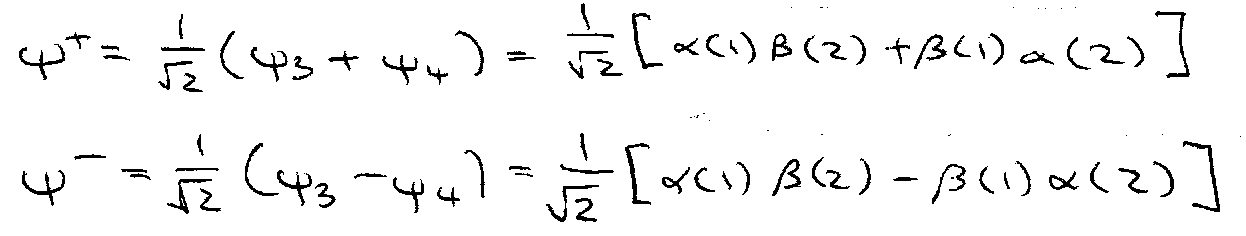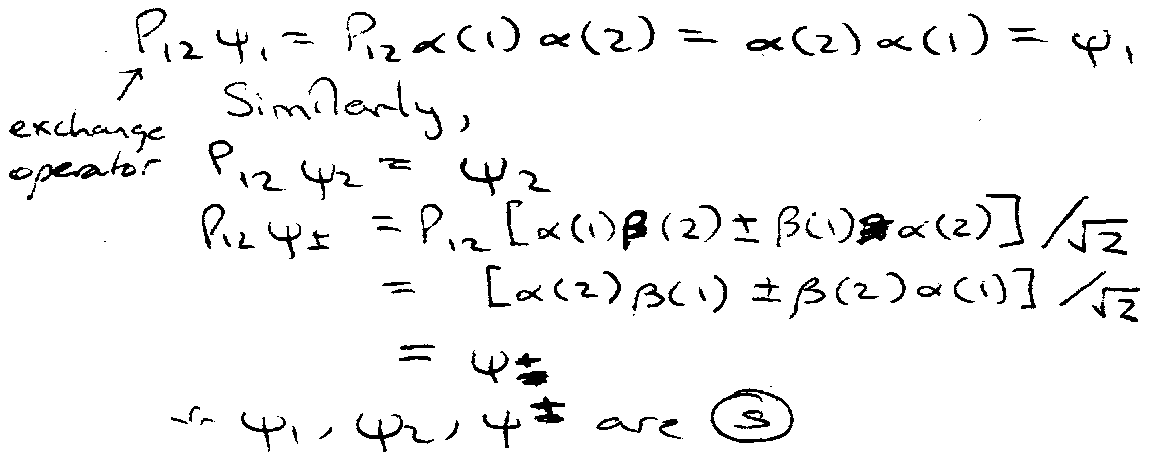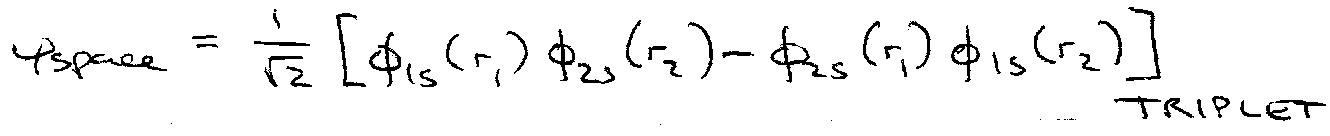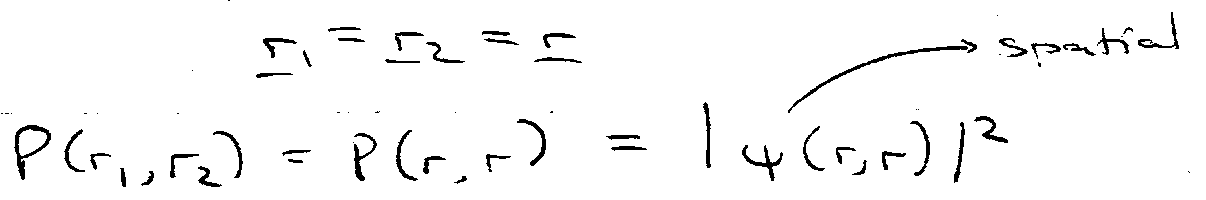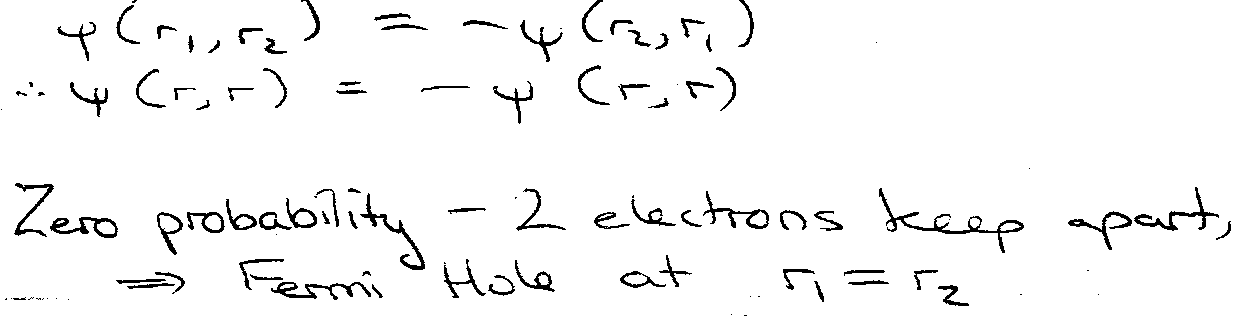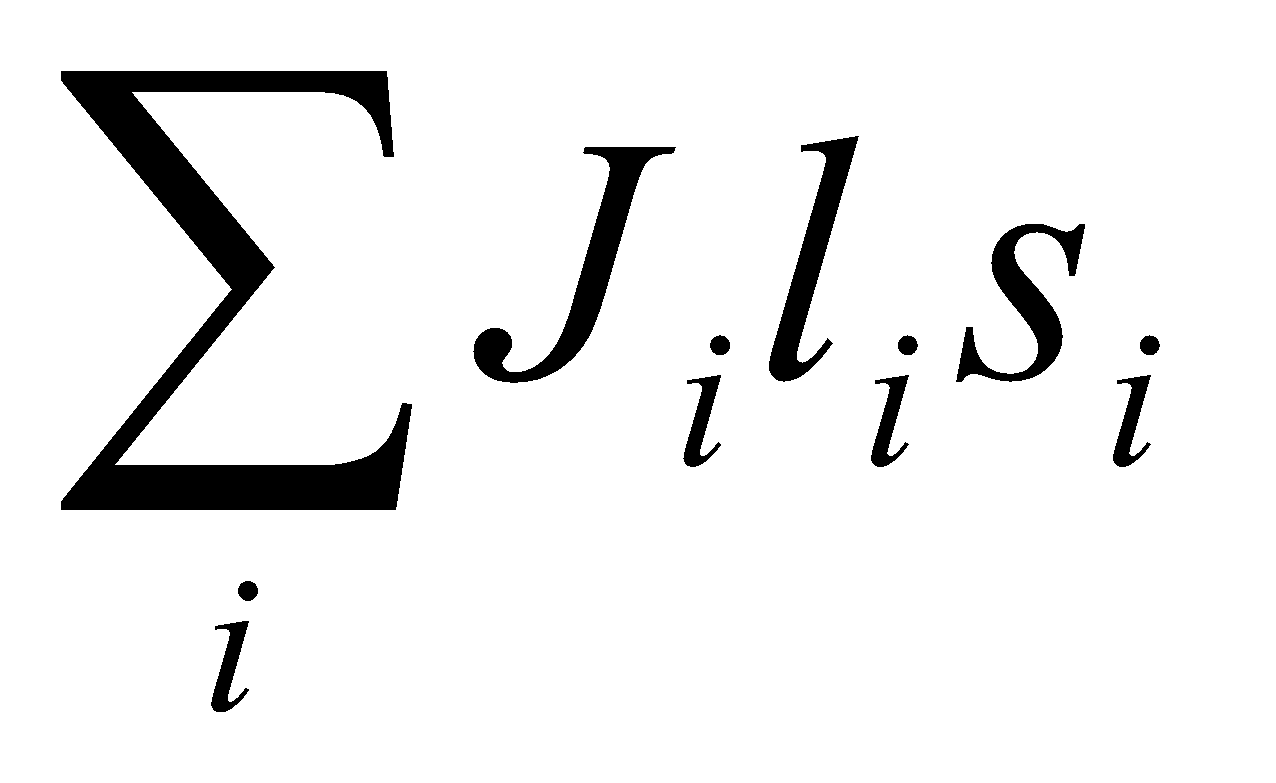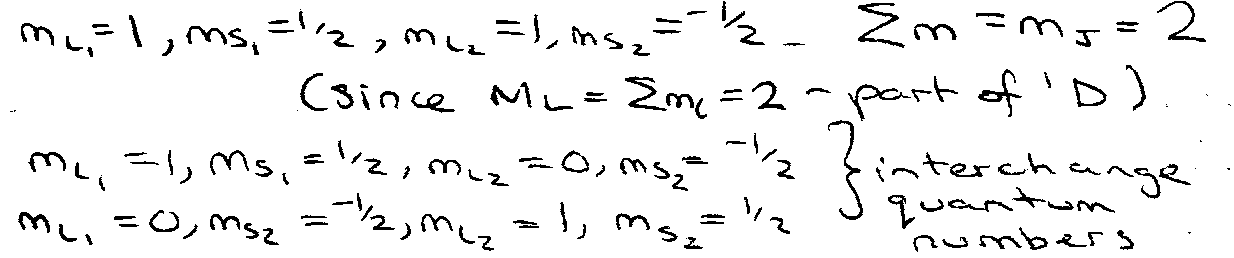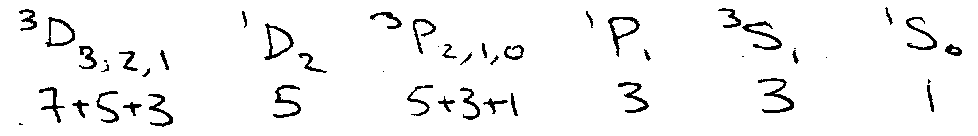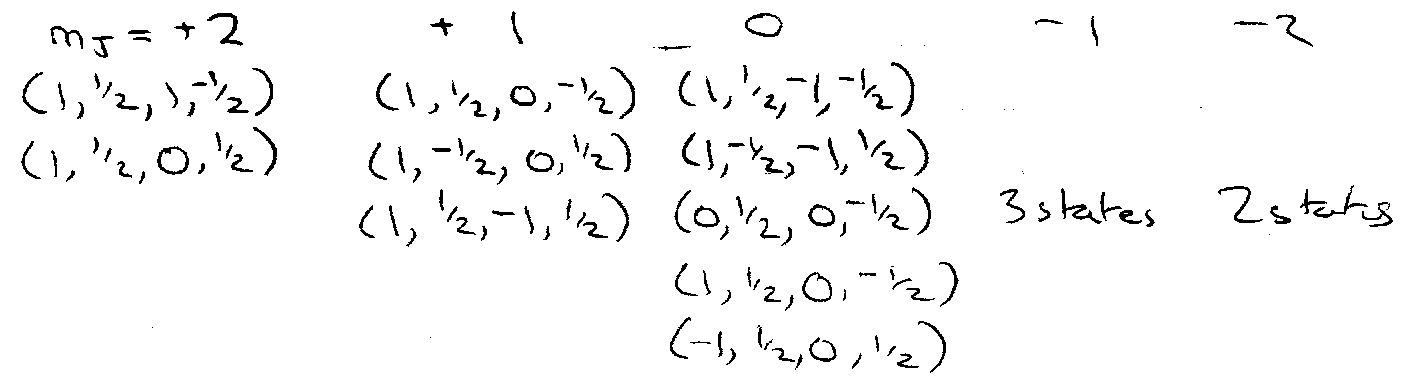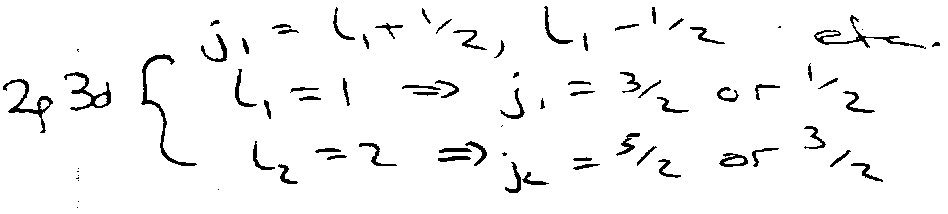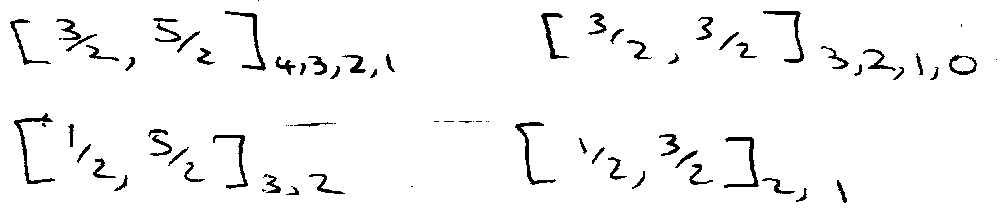Atomic Spectroscopy Notes

Expected: knowledge of Quantum + Perturbation Theory: calculating eigenfunctions that are difficult by using:

where H’ is a perturbation on Ho (zeroth order wavefunction). 1st Order:

E = Eo + <H’>

Angular Momentum –

Measure of torque required to stop a body rotating.

Single particle: l = r^p, where l is vector perpendicular to plane of rotation.

| l2 | = lx2 + ly2 + lz2

lz =

l2 = - h2 Λ2                 

Commutation –

[ l2, lz ] = [ l2, lx ] = [ l2, ly ] = 0

[ lx, ly ] = ihlz

[ ly, lz ] = ihlx

[ lz, lx ] = ihly

Electrons in atoms:

[ l2, H ] = 0 and [ lz, H ] = 0

Thus, energy, square of orbital angular momentum and one of its components can all be simultaneously specified (eigenvalues).

Hydrogenic (1e) Atoms –

Spherical Symmetry → polar coordinates preferred.

Boundary Conditions,

ψ finite for all r (including origin).

ψ→0 as r→∞.

ψ(r,θ,φ) = ψ(r, [θ+2nπ], [φ+2mπ])        n, m integers.

Separate,

ψ = R(r) Y(θ,φ)                        Radial and Angular components

Solutions as,

ψn,l,ml = Rn,l(r) Yl, ml (θ, φ)

 Quantisation,

Solving,

Only Λ2 can change Y(θ,φ) variables, therefore for a valid solution it is implied that this does not happen, i.e.

Λ2Y(θ,φ) = C Y(θ,φ)                [ C = constant ]

Make substitution to remove angular parts:

Angular ψ identical to particle on a sphere, i.e.

Treat θ as constant,

This is a particle on a ring,

Subbing 2 into 1,

Choose A = 1/√2π and B = 0 (Normalised).

Subbing in (1) & (2) into (0):

Solve to give Associated Legendre Functions. Boundary Condition gives rise to l quantum numbers.

Sub this into A and let P(r) = r[R(r)]:

Veff – effective potential energy → true V + correction for centrifugal E(l).

Solve (3) as R(r) → 0, r → ∞ and R(r) finite.

Quantum Numbers –

1. Principle Quantum Number, n.

Determines energy. Determines mean radius of electron orbital. For l = 0,

2. Orbital Angular Momentum, l

Determines “shapes” – angular distribution. Angular momentum.

L is a vector of length [ l(l+1) ]1/2 h, where l has integral values o → n-1.

Electrons with different l have different radial wavefunctions, because of centrifugal effect.

3. Magnetic Quantum Number, ml

Projection of orbital angular momentum on a given axis → Direction of orbital.

<lz> = mlh

ml takes values –l, -l+1, …, +l

i.e. (2l+1) values in total.

Eigenvalues and Eigenfunctions

For H atom, E is independent of l and ml. Note: for p orbitals, l = 1. px, py, pz ≠ ml = 0, ±1.

Real linear combinations:

ψpz = | n, l=1, ml=0 >

For degenerate orbitals, any linear combination is a solution of the Schrodinger Equation.

Solutions to the Schrodinger Equation (1 electron)

R almost constant (depending on atomic number).

Yl, ml (θ,φ) – complex, but independent of n.

Rnl(r) – near nucleus varies as rl, but large distances varies as exp [ - Zr/nao ]

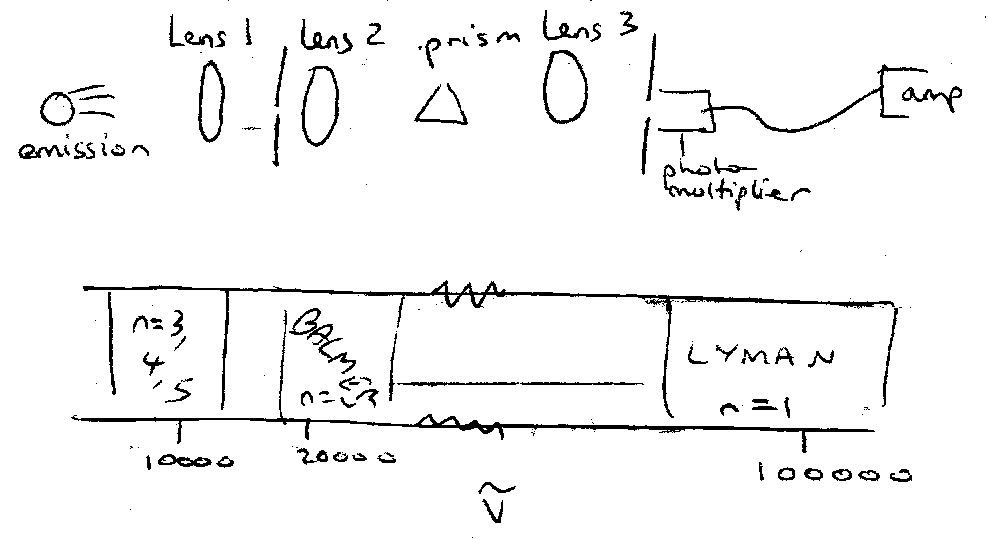
Spectrum of a Hydrogen Atom

Experimental – low pressure electric discharge in H2

• accelerated electrons / ions cause dissociation, ionisation and excitation.
• Electron / proton recombination also important.

Light emitted by excited H atoms analysed by spectrometer. Observe distinct series:

	Lyman (UV)	Balmer (vis)	Paschen (IR)
Emit down to:	n=1	n=2	n=3

(in absorption observe Lyman only).

Transition Energies:

Wavenumber, v = ΔE/hc.

Note the dependence on R, and also the slight isotope dependence of R.

He+ -

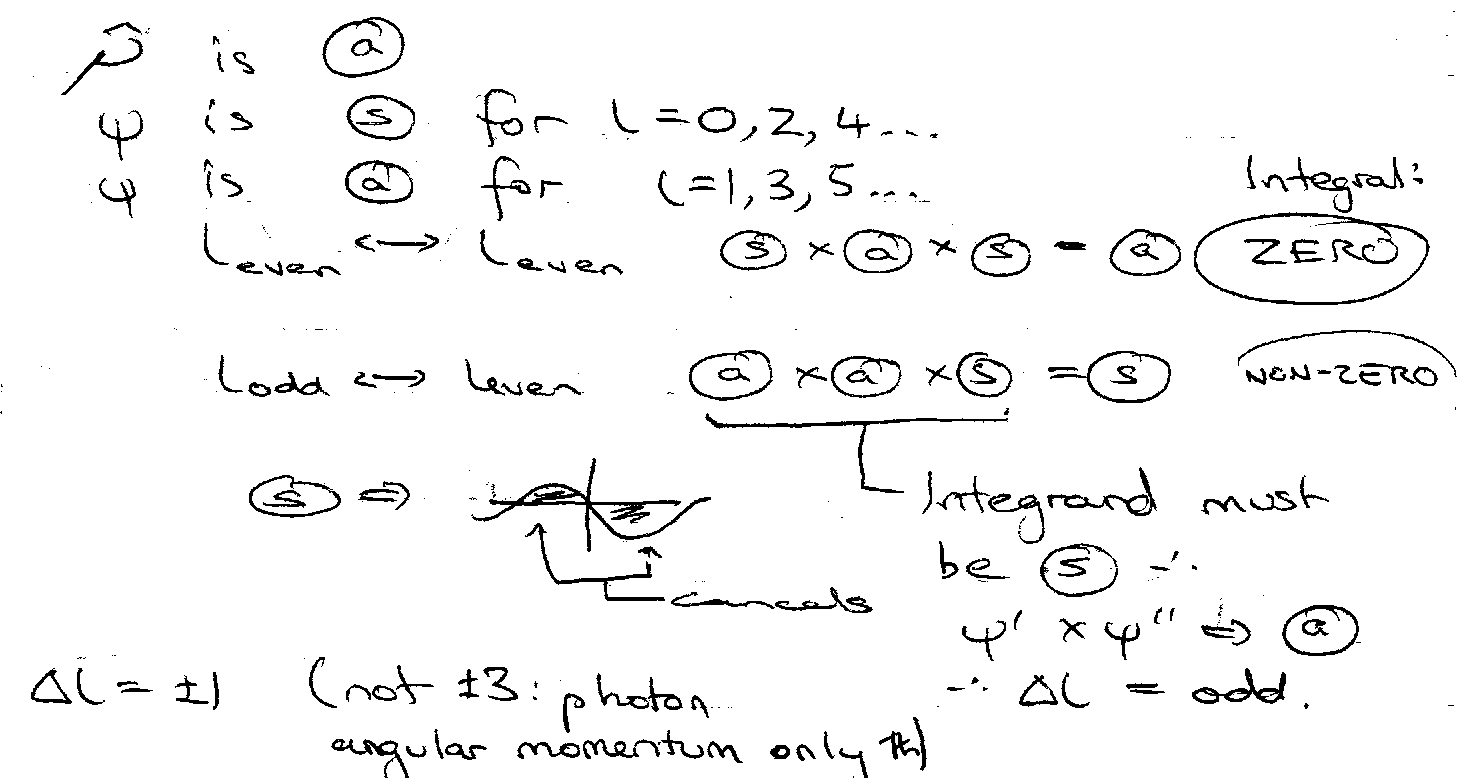
Selection Rules – which transitions are allowed.

Δn = anything integral.                Δl = ±1.                        Δml = 0, ±1.

This comes from:

Consider symmetry wrt inversion:

x,y,z → -x,-y,-z

Electron Spin –

Inferred empirically from very high resolution spectra.

• splittings due to extra degree of freedom.
• Intrinsic angular moment of electron “spin”.
• Quantum number s = ½ only.

Spin Angular Momentum =

Degeneracy –

For each n → n values of l, l = 0, 1, … (n-1)

For each l → (2l+1) values of ml, ml = -l, -l+1, … +l.

Implies total degeneracy of n2 for each. Including spin → 2n2 degenerate.

Spin-Orbit Coupling

Spin possesses a magnetic moment.

Orbiting electron creates a magnetic field “seen” by the electron spin. Field due to relative motion of charges – nucleus orbits electron!

Causes coupling of l and s to give total electronic angular momentum, j = l + s.

j2, jx2, jy2, jz2 – same commutation properties as l equivalent.

j2ψ = j(j+1)h2ψ

jzψ = mjhψ

For one-electron case, j is half-integral = l ± ½. mj takes values j, j-1, … -j, i.e. (2j+1) degenerate.

< l.s > is evaluated using j = l + s, j2 = l2 + s2 + l.s

Term Symbols

2S+1Lj , e.g. 3d → 2D5/2, 2D3/2

Spectrum Including S-O Coupling

New selection rules –

ΔJ = 0, ±1

Δmj = 0, ±1

Δn = anything        

Δl = ±1

Lamb Shift – quantum field effect. Also relativistic increase in mass with velocity.

Alkali Metals – many electron atoms

Schrodinger –

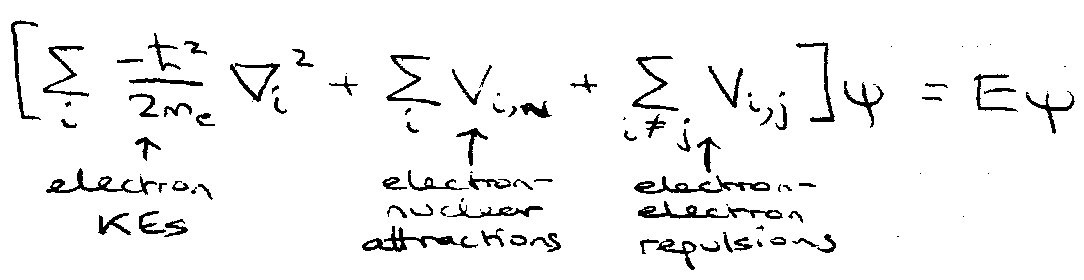
Energies, E, include the energies of all electrons and all interactions:

Orbital Approximation –

Assume,

1e equation solved by numerical method using self-consistent field approach:

• each electron moves in an orbital in the average field of the other electrons.
• Energies = “orbital energies”.

Not quite true, should obey Pauli Exclusion and be linear combination, e.g.

φa(r1) φb(r2) ± φa(r2) φb(r1)

Total wavefunction has to be antisymmetric with respect to interchange of electron coordinates.

Self-Consistent Field Approach

Total Energy is not just sum of orbital energies, i.e. ΣεI because e-e repulsion is counted twice.

NB: as for H atom:

Electron Configuration – which orbitals occupied and how many electrons (Pauli).

Use orbital approximation.

Determine Ground State by Aufbau and Pauli Exclusion Principles

Li: 1s22s1                Na: 1s22s22p63s1

etc.

Spectra of Many Electron Atoms

Within Orbital Approximation, can only change orbital of 1 electron during transition, e.g.

Main concern is valence electron excitation. Core electrons can be excited, but much higher energy (ionisation may occur).

Selection Rules for Alkali Metals

Closed shell core – no resultant spin or orbital angular momentum.

Alkali Metals → pseudo-1s atom, so same selection rules as for Hydrogenics.

Comparison with H-atom –

1. different l-states of same n are non-degenerate, due to effects of e-e repulsion (penetration and shielding).
2. Bigger spin-orbit coupling (low resolution spectra → observable).

Penetration and Shielding –

Effects of valence electron ↔ core electron repulsion.

Consider Li,

In 1s23d excited configuration, 3d orbital is almost completely outside the core.

• experiences attraction to +3 nucleus
• but repulsion due to core electrons
• act like a -2 point charge “shielding”.

Net Effective Nuclear Charge ≈ +1.

In 1s22s1 configuration, substantial penetration of 2s electron inside 1s2 core → incomplete shielding, Zeff ≈ + 1.28.

1s22p – 2p electron less penetrating. Zeff ≈ + 1.02.

Therefore 2s electron is more tightly bound than 2p, therefore lower in energy.

NB: also 2s orbital in Li lower in energy than in H-atom. Same true for 2p, but not as different.

In general, ns < np < nd < nf, etc.

Sodium Atom Spectrum

1. 3s → 3p – lowest energy transition in absorption.

cf. H atom 3s and 3p approximately degenerate.

2. Several series:

ns → 3p                SHARP

np → 3s                PRINCIPAL – also present in absorption

nd → 3p                DIFFUSE

nf → 3d                FUNDAMENTAL – almost same E as H-atom transitions

3. Spin-Orbit Splitting –

Same j states obtained as in H-atom but hydrogenic theory does not work.

Splittings larger. Increase with Z (not as rapidly as Z4).

cf. spin-orbit coupling constants:

Li(2p)	0.3 cm-1	H (2p)	0.243 cm-1
Na (3p)	17.2 cm-1	H (3p)	0.072 cm-1
K (4p)	57.7 cm-1	H (4p)	0.031 cm-1

Quantum Defect –

For H-atom, E = IE – hcR/n2

For alkali metals, effects of e-e repulsion means energies lower than predicted by Rydberg formula (above).

Enl =

Where νnl is effective principal quantum number.

Define the quantum defect,

δnl = n - νnl

Enl =

For a given l, it turns out that δnl is almost independent of n → δl.

Electrons spend such short time close to the nucleus that its behaviour is almost independent of n. Therefore transition energies:

For a given series (common n’ l’):

ΔE =

A plot of ΔE against 1/(n-δl)2 gives straight line (adjust δl for best fit).

NB: Ionisation Energy = where nl is the lowest state.

Helium Atom

New Features – 2e in unfilled shells (except Ground State) → 2 sources of orbital and spin angular moment. New important effects on energy levels and degeneracies.

Orbital Angular Momentum –

Primarily concerned with configurations 1snl. Doubly excited states are unstable wrt ionisation.

1s electron has l = 0, therefore total orbital angular momentum is the angular momentum of the excited electron, l. Total orbital angular momentum L = l.

Spin Angular Momentum –

Both electrons have s = ½, ms = ½ or -½ (α or β).

Ground State (1s2)

Pauli → ms1 = ± ½ and ms2 = ½

Spin paired (antiparallel) → “singlet” state.  

Resultant s = 0, ms = 0.

Excited Configurations, 1snl

- no restrictions on ms1, ms2 from Pauli.

Spin Parallel → resultant magnetic moment.

Spin Paired (opposed) → no resultant magnetic moment.

Define total spin angular momentum, S = s.

| S | = √(s(s+1)) h.

- shows same commutation relationships as other angular momentum operators.

→ quantisation.

In general triplet state has lower energy than singlet state from same configuration.

Selection Rules –

New rule, ΔS = 0.

Therefore singlet ↔ triplet is forbidden.

In Absorption:

Observe 1s2 (1S0) → 1snp (1P)

In Emission:

Use discharge lamp – ionisation followed by recombination

He+ + e- → He* → emission

Excited atoms formed in configurations.

1snl (1L) or 1snl (3L)

As ΔS = 0, two sets of transitions observed.

Singlet ↔ singlet or triplet ↔ triplet.

1s electron shields outer electron from nucleus.

Penetration effects → different l states have different energy.

ns < np < nd < nf etc.

Spin-Orbit Coupling in many electron atoms –

J = L + S → J2 and Jz quantised.

Quantum Numbers:

J = L + S, … , | L-S |

MJ = J, J-1, …, -J.

NB: can only occur for triplet states in Helium.

e.g. S = 1, L = 1 → 3P         “Term”

J = 2,1,0 → 3P2, 3P1, 3Po        “Level”

Additional Selection Rules:

ΔJ = 0, ±1                                ΔMJ = 0, ±1

NB: in He, spin-orbit interaction is very strong → very small splittings.

Spin Wavefunctions and Pauli Principle

For a 2e system:

For Helium excited states, each electron can have ms = ± ½ (represent ψ by α and β).

This suggests 4 possibilities:

ψ3 and ψ4 have Ms = 0.

Neither singlet nor triplet – electrons are indistinguishable.

Wavefunction must contain both possibilities with equal weighting. Two ways:

Equal probability of electron 1 or 2 being in spin state α or β.

Pauli Principle –

Total ψ must be antisymmetric wrt exchange of any 2 electrons (applies generally to all identical half-integral particles).

Therefore ψtot = ψspaceψspin = antisymmetric wrt interchange.

Consider spin, ψ1ψ2ψ±

Hence, ψspace must be antisymmetric.

e.g. 1s2s configuration with ψspin symmetric.

Conversely,

Why is Triplet Lower in Energy than Singlet?

“Fermi Hole”

Probability of finding both electrons at same point in space.

For Triplet –

For Singlet –

Therefore for triplet state electrons must stay further apart → less repulsion.

Not whole truth though, as in triplet state, 1s electron is less shielded, therefore nl orbital is slightly more compact than corresponding orbital in singlet state.

Angular Momentum Coupling in many electron atoms

General atom – more than 1e with both orbital and spin angular momentum.

e.g. C – 1s22s22p2. Excited states: 1s22s22p3d, etc.

Configuration split into energy levels by 3 types of interaction –

1. spin correlation (couples spins, electrostatic).
2. Orbital electrostatic interaction.
3. Spin-Orbit Coupling (magnetic).

Pattern of energies, quantum numbers, etc – depend on which effect is largest.

Russell-Saunders Coupling (L-S Coupling)

1. >~ (b) >> (c) – common for light elements.

a) Define S = Σsi –sum of spin angular momenta.

e.g. S = s1 + s2, … | s1 – s2 | for 2 electrons.

b) L = Σli – resultant orbital angular momentum.

e.g. L = l1 + l2, l1 + l2 – 1, … | l1 – l2 |

Good quantum numbers L & S → ψtot is eigenfunction of L2 and S.

e.g. for a 2p 3d configuration:

l1 = 1, l2 = 2, → L = 3,2,1 (F, D, P)

s1 = ½, s2 = ½ → S = 1, 0.

→ Terms are 3F, 1F, 3D, 1D, 3P, 1P.

Singlet-Triplet Splitting – due to spin correlation.

Splitting of different L values – due to different electrostatic repulsions (different orbitals).

For max L – electrons “orbit” in same direction.

For min L – electrons “orbit” in opposite directions (→ more repulsions).

If spin-orbit interaction small – spin and orbital angular momenta couple → Total Angular Momentum J = L + S.

Hence Quantum Number J = L + S, L + S -1 …

e.g. 3F: S=1, L=3 → J = 4,3,2.

Degeneracies –

Each state J is (2J+1) degenerate.

MJ = J, J-1, .. –J.

For 2p 3d configuration there are 60 states.

Lande Interval Rule –

Spin-orbit Hamiltonian, HSO =

Approximate by hcA L.S

Terms from Configurations with Equivalent Open-Shell Electrons

e.g. for 2p2 configuration two equivalent 2p electrons.

Pauli Principle → restrictions

Would expect l1 = 1, l2 = 1, s1 = ½, s2 = ½.

→ 3D, 1D, 3P, 1P, 3S, 1S.

In fact only get 1D, 3P, 1S – why?

Microstates in decoupled representation

Consider 2p3d configuration again.

In limit when all couplings → 0, the defined quantum numbers would be:

l1, ml1, s1, ms1, l2, ml2, s2, ms2.

The 2p3d configuration would then be:

(2l1+1)(2s1+1)(2l2+1)(2s2+1) = 3 x 2 x 5 x 2 = 60-fold degenerate.

NOTE: Couplings do not create any new states – they only lift degeneracies.

Furthermore, number of states with given value of ml1 + ms1 + ml2 + ms2 = # of states (in L-S coupling) with same value of mJ.

Returning to 2p2 configuration, consider possible microstates, can have situation with both electrons have same n, l, ml – NOT ALLOWED

Electrons indistinguishable → 1 microstate.

Consider all possibilities:

Total number of microstates only 15 (not 60).

NB: Degeneracies in L-S representation.

Group Microstates according to Σm (obeying Pauli Principle)

No Σm = ±3 states → no 3D3 → no 3D.

2 Σm = ±3 states → both 1D2 and 3P2.

1D requires 1mJ=2, 1mJ=1, 1mJ=0, 1mJ=-1 …

3P requires 1mJ=2, 2mJ=1, 3mJ=0, 2mJ=1 …

After counting all these states, leaves one other → 1So.

(See Tutorial Question)

Order of Quantum States – Hund’s Rules

For a given configuration with LS coupling – order of states normally given by:

1. Terms with largest S, i.e. lie lowest in energy.
2. For given S, terms with largest L are lowest, e.g.

3. For less than half full shells lowest J-value has lowest energy.

For more than half full shells highest J-value has lowest energy.

(S.O constant. A is negative).

Note – p4 has same terms as p2, therefore O similar to C, but J order reversed:

For d2, obtain 3F2 < 3F3 < 3F4.

For d8, obtain 3F4 < 3F3 < 3F2.

Spectra of L-S Coupled Atoms

Selection Rules:

Δn = anything                                Δl = ±1                                ΔS = 0

ΔJ = 0, ±1 (but not J=0 ↔J=0)        ΔL = 0, ±1                        ΔMJ = 0, ±1

NB: heavier elements show “intercombination” lines e.g. 5S → 3P (ΔS = 1)

Spin-Orbit coupling can weakly mix states of different S = breakdown of L-S Coupling scheme.

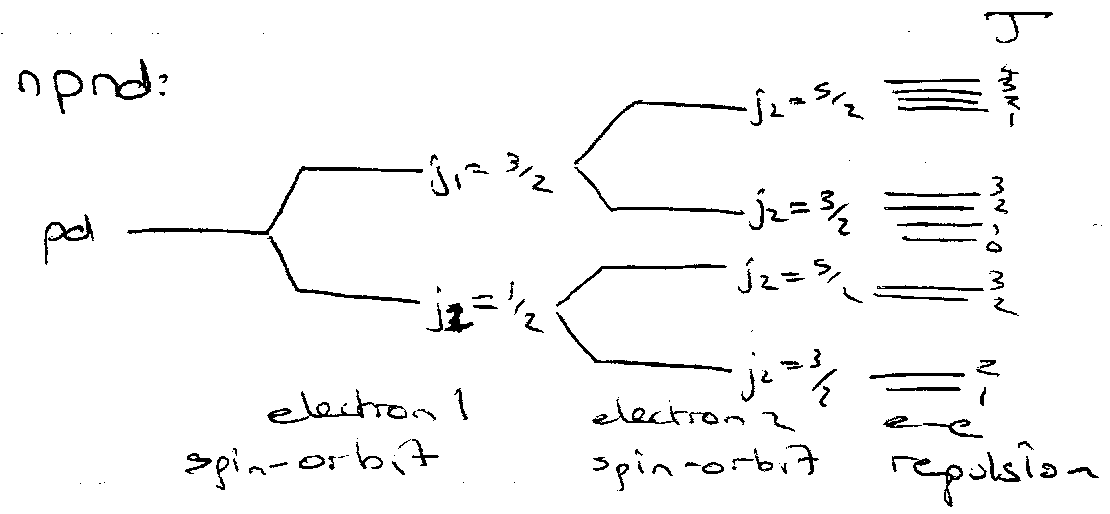
j-j Coupling

Occurs when spin orbit coupling is large compared to spin correlation or orbital/orbital interaction.

NB: spin-orbit coupling is a magnetic interaction and magnetic fields are relativistic electric fields, therefore coupling large for heavier atoms.

If spin-orbit coupling sufficiently large, the spin and orbital angular momentum of each electron coupled → j.

e.g.

l1 + s1 = j1        MAGNETIC

l2 + s2 = j2        MAGNETIC

j1 + j2 = J        ELECTROSTATIC

Quantum Numbers,

Now couple j1 and j2 to give J states, written as:

Note: L & S no longer defined – no 1P, 3P, etc.

Spectra in j-j Coupling

Selection Rules:

Δl = ±1, Δj = 0, ±1 for 1 electron and Δl = Δj = 0 for other electrons.

ΔJ = 0, ±1                                        ΔMJ = 0, ±1

Energy Levels (j-j) –

Determined by j1 and j2:

No L or S, therefore no S/L selection rules.

j-j coupled states are a mixture of singlet and triplet components.

Some atoms show intermediate behaviour, therefore neither L-S or j-j selection rules are obeyed.

Group IV Atoms –

C = L-S Coupled

Si

Ge        intermediate

Sn
Pb = j-j Coupled