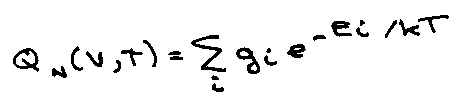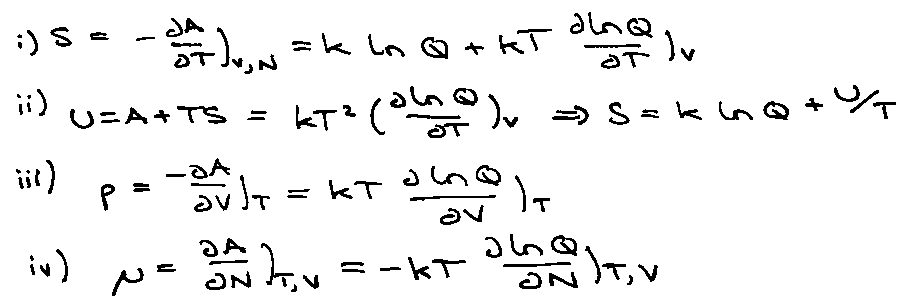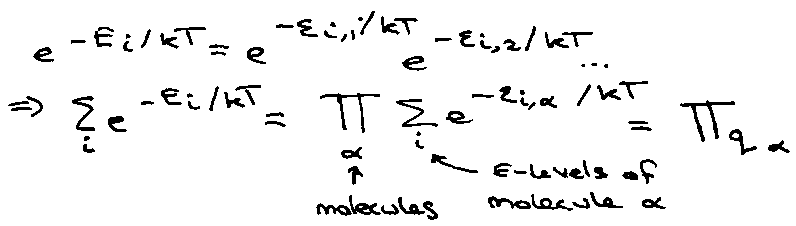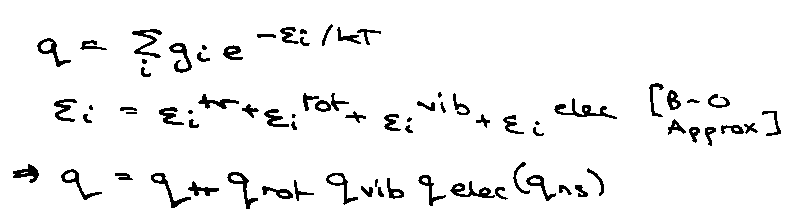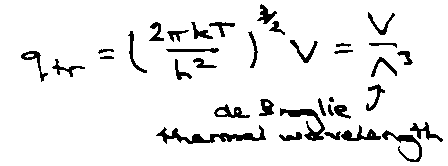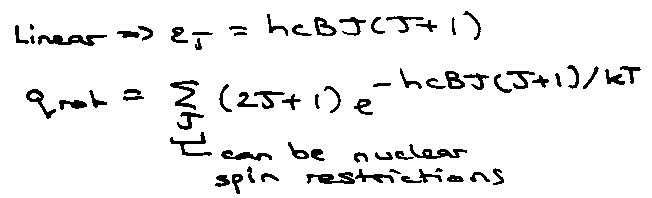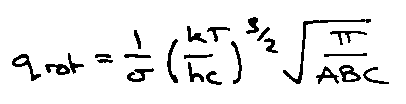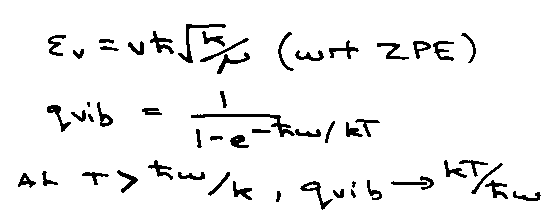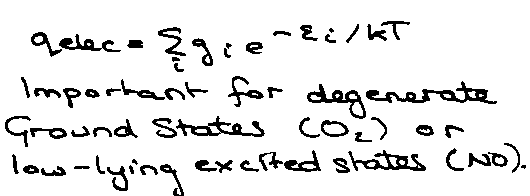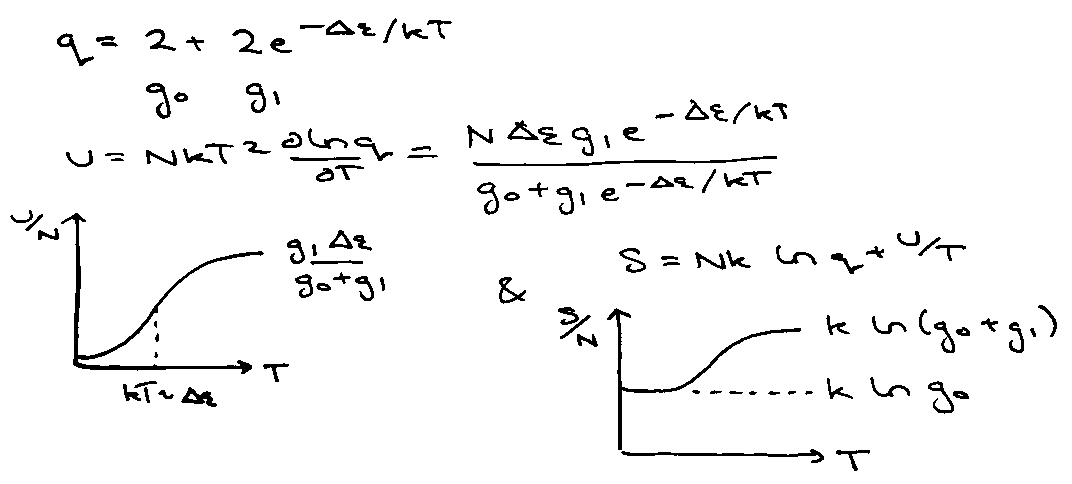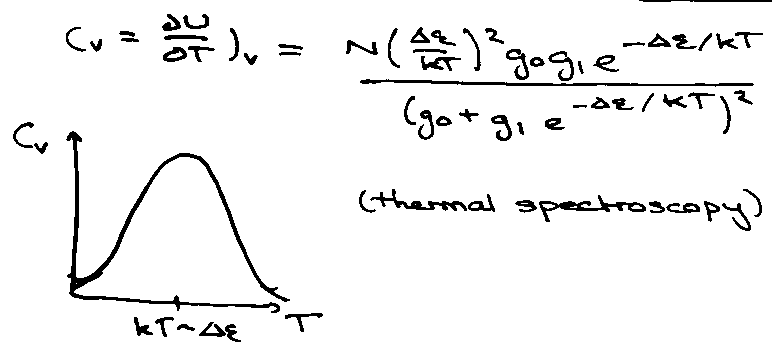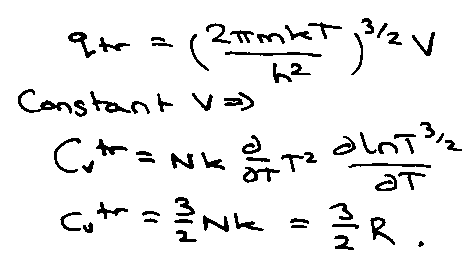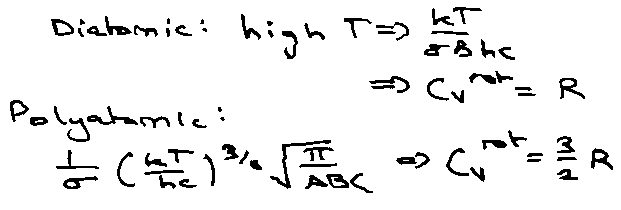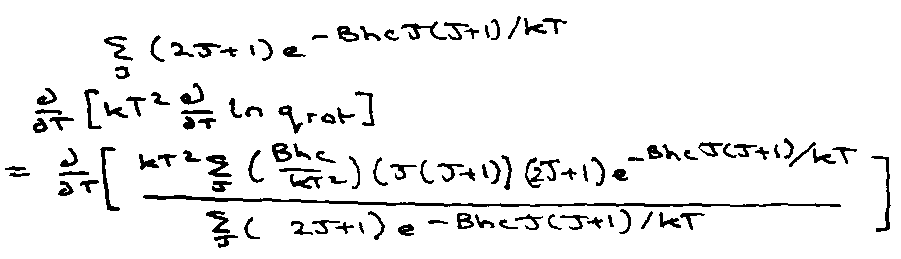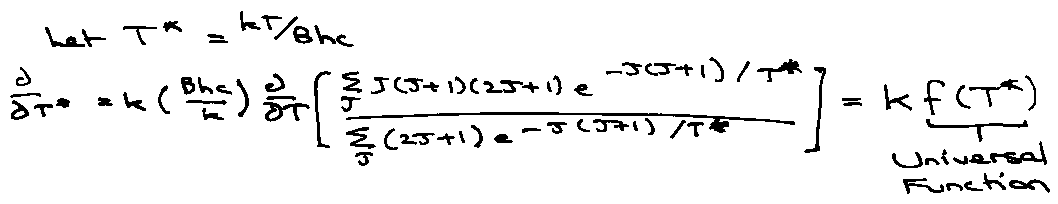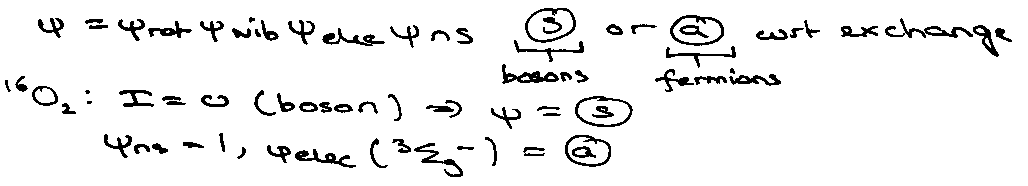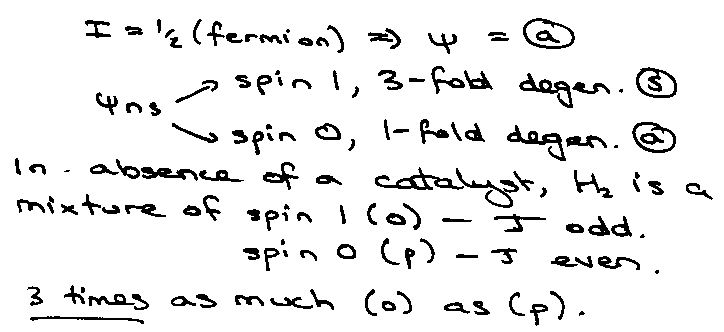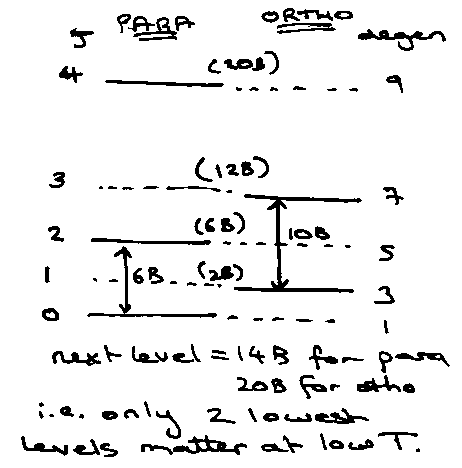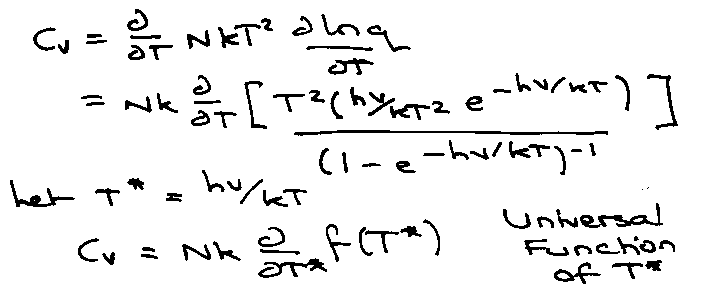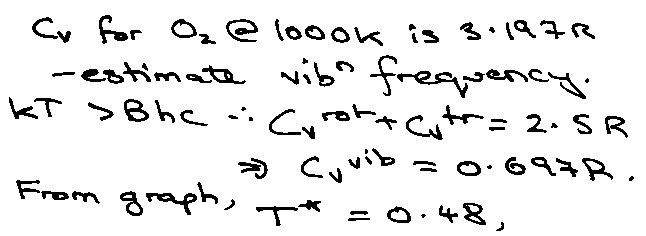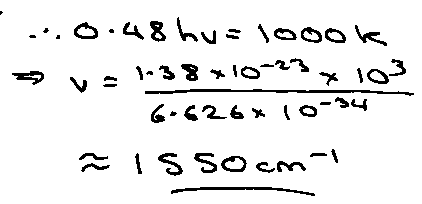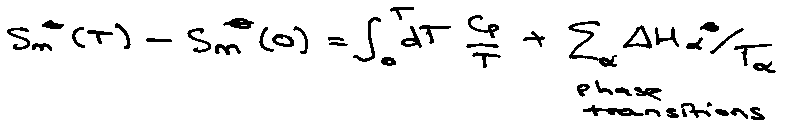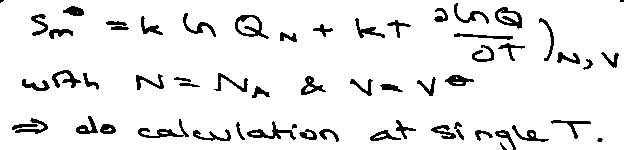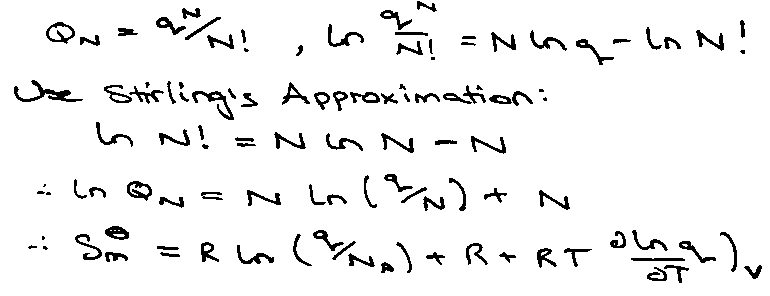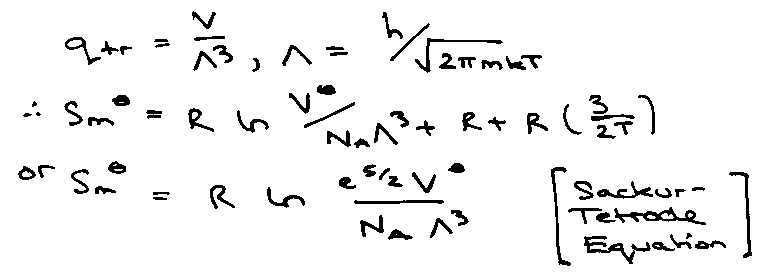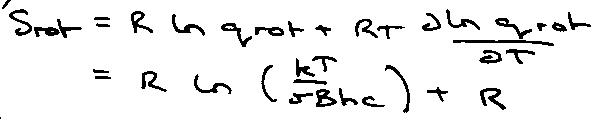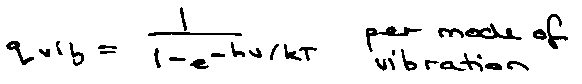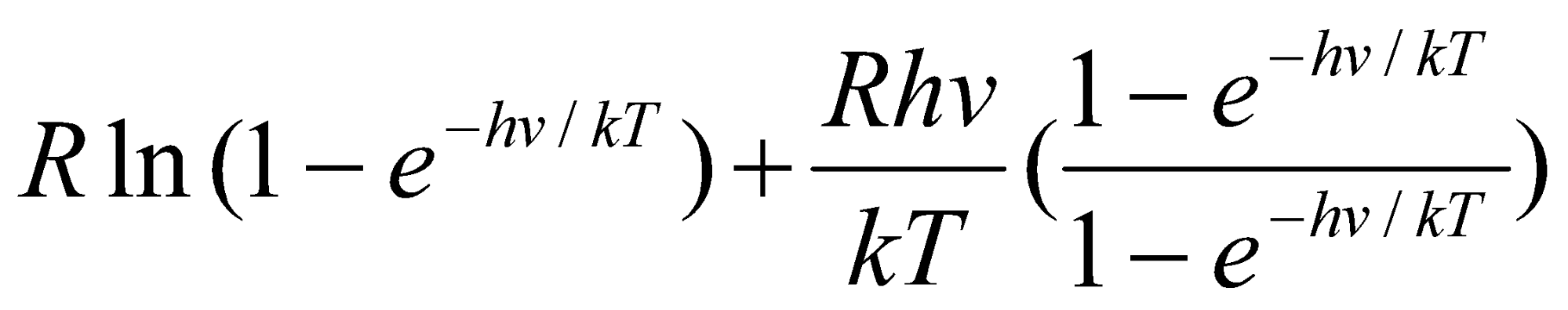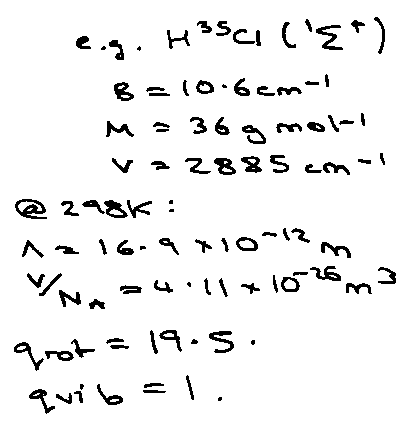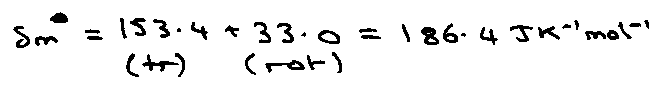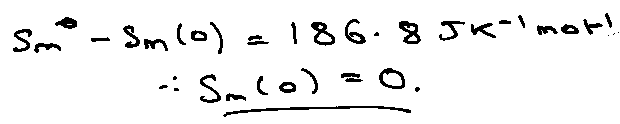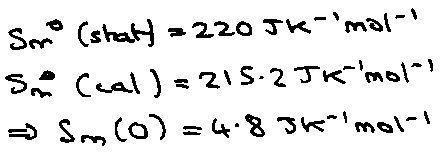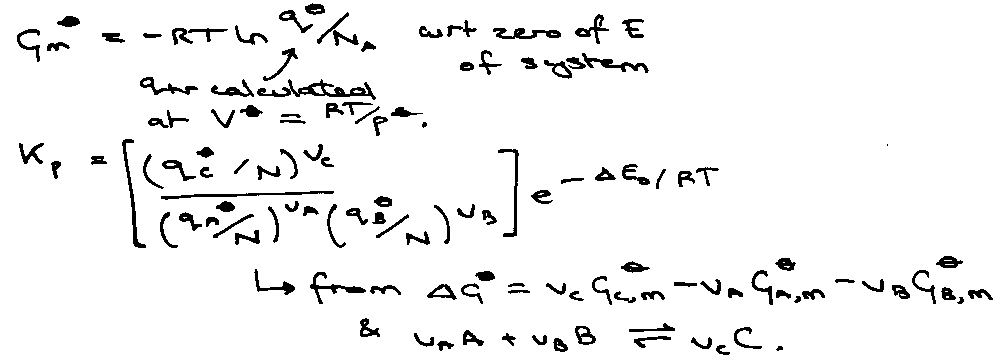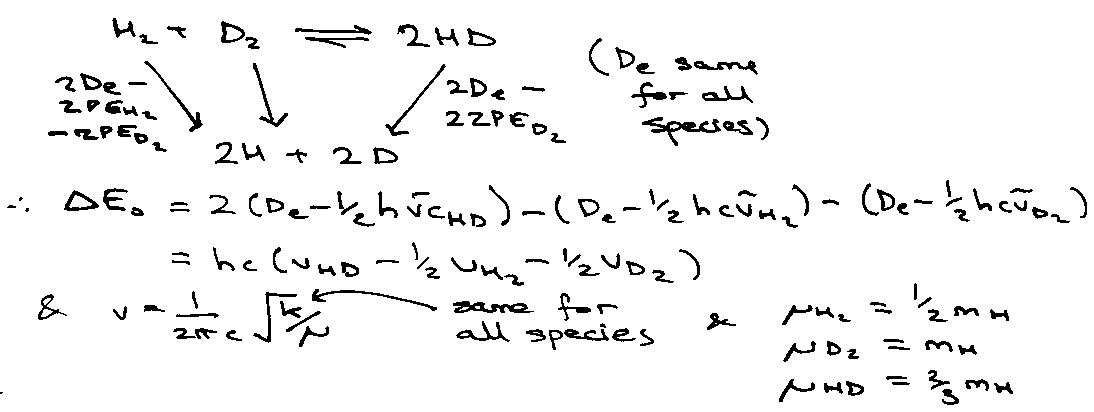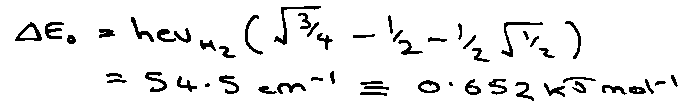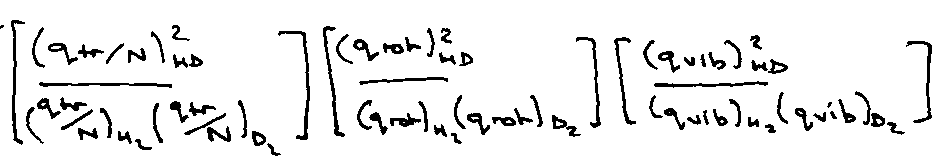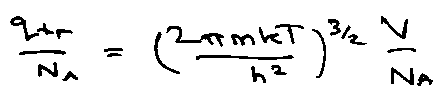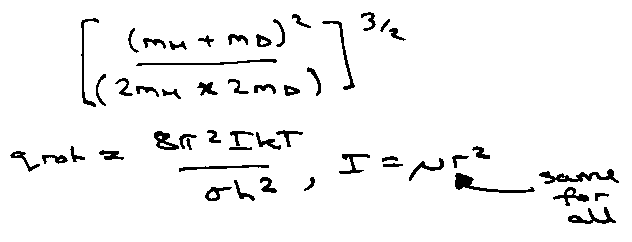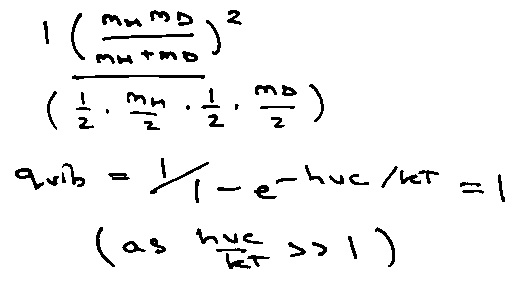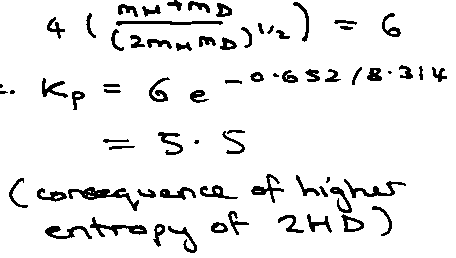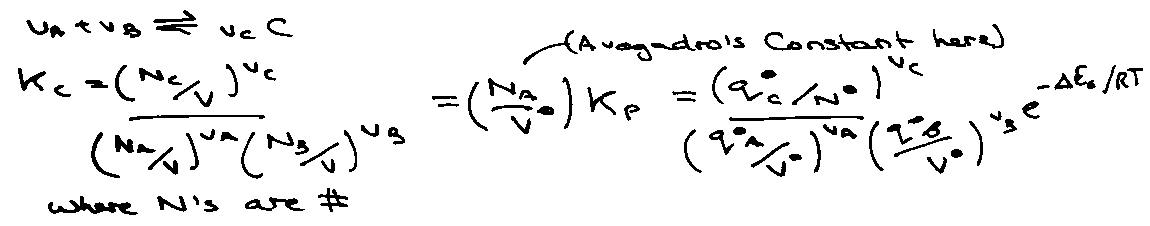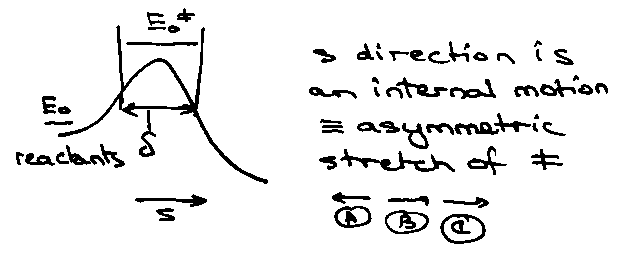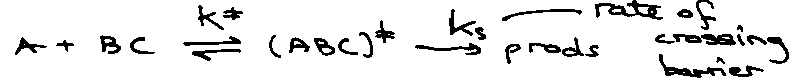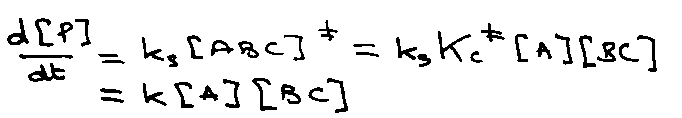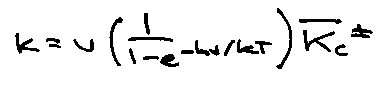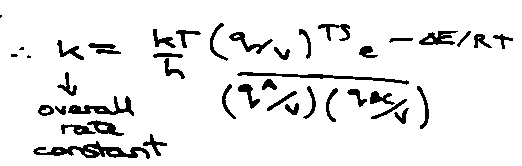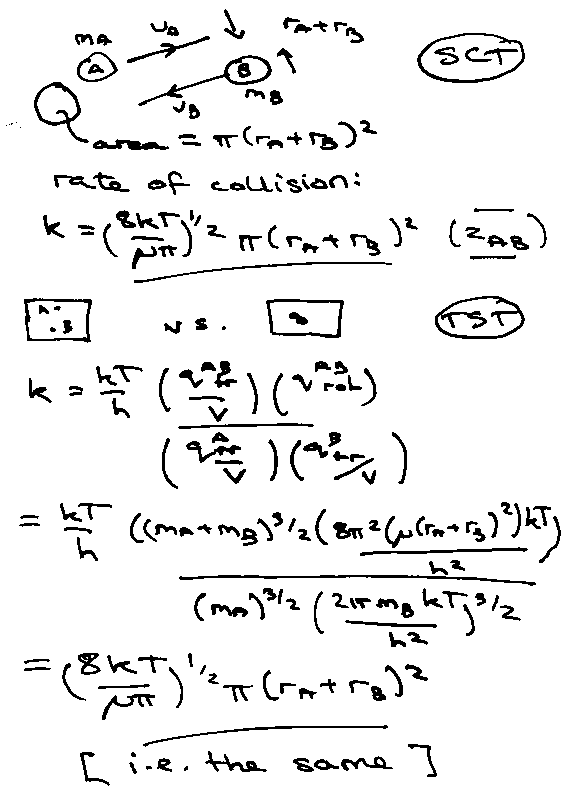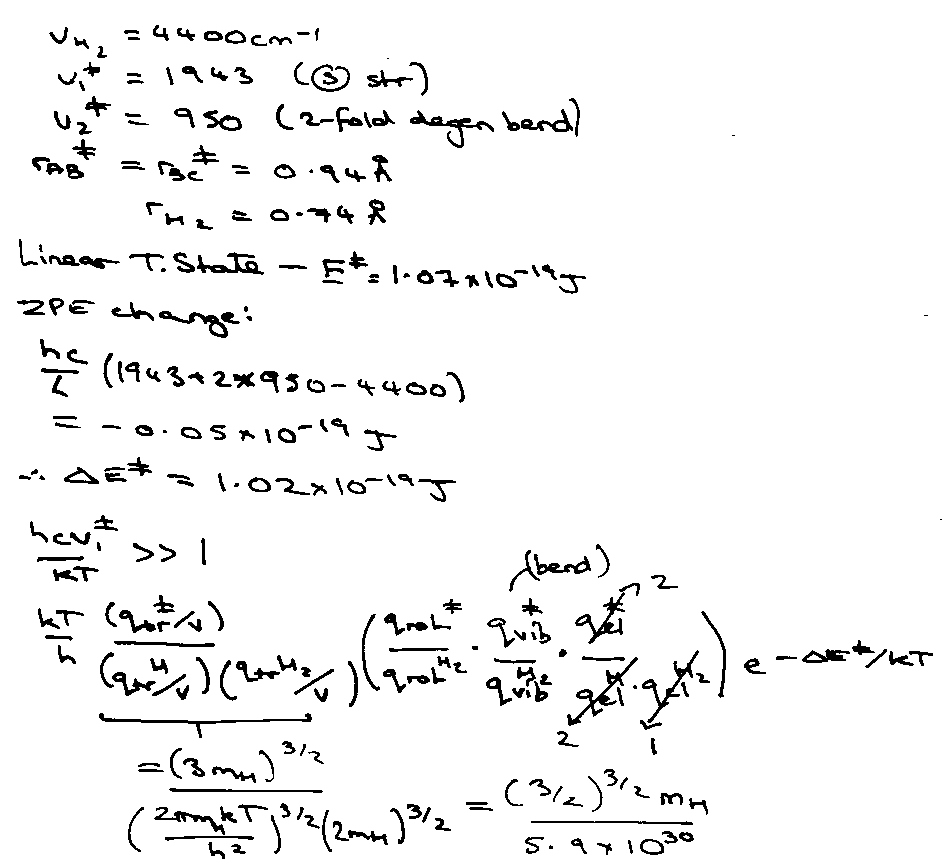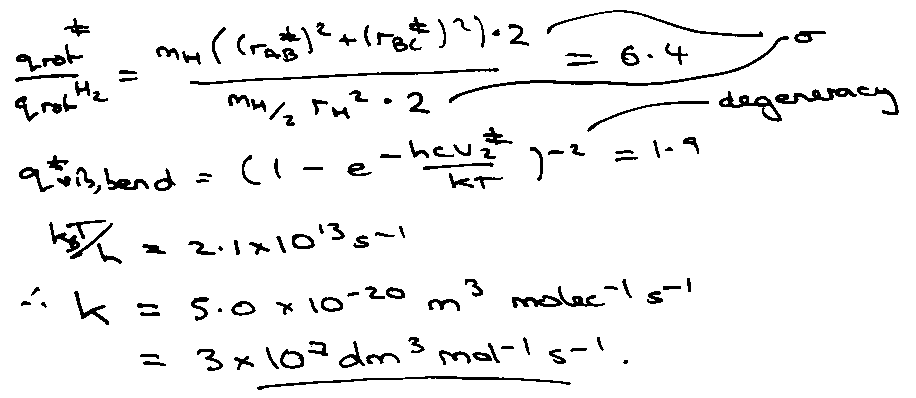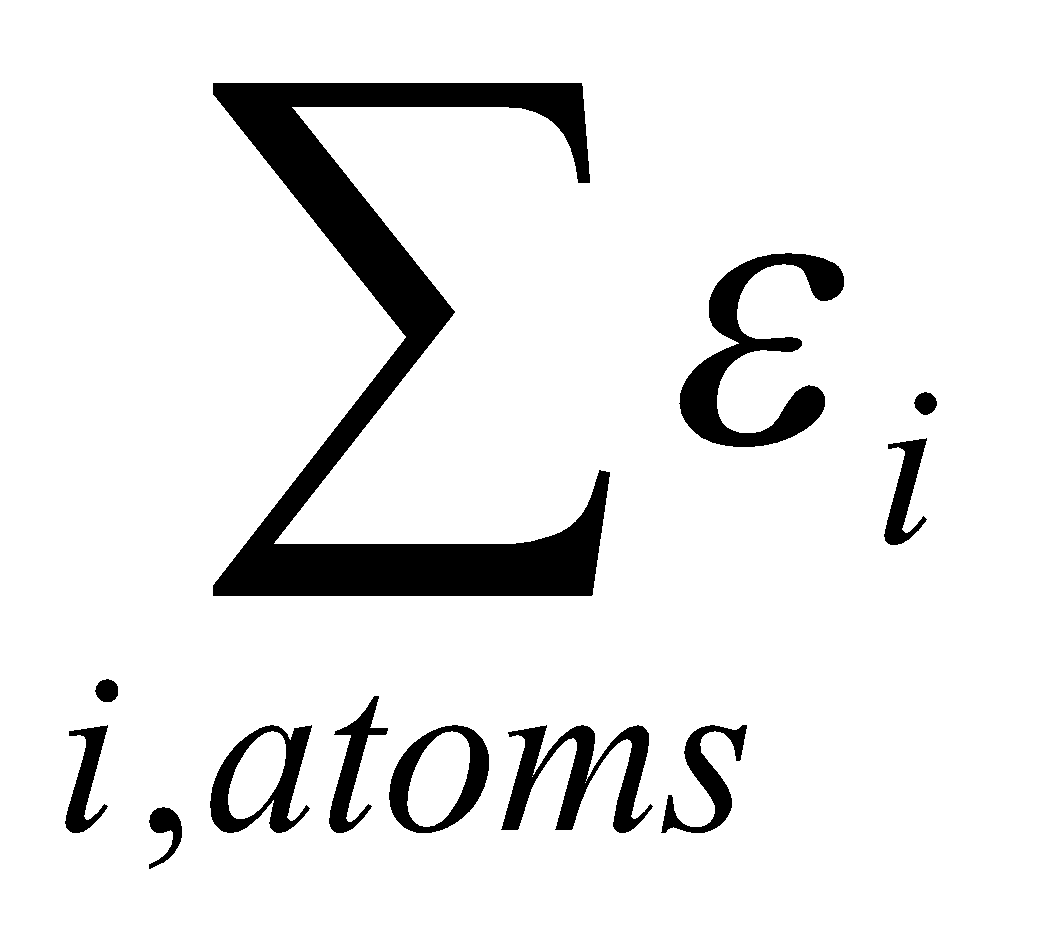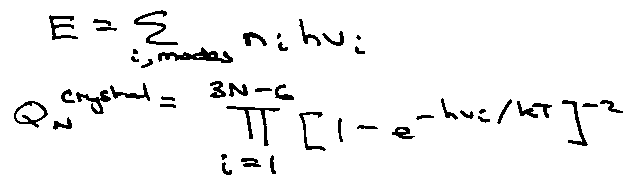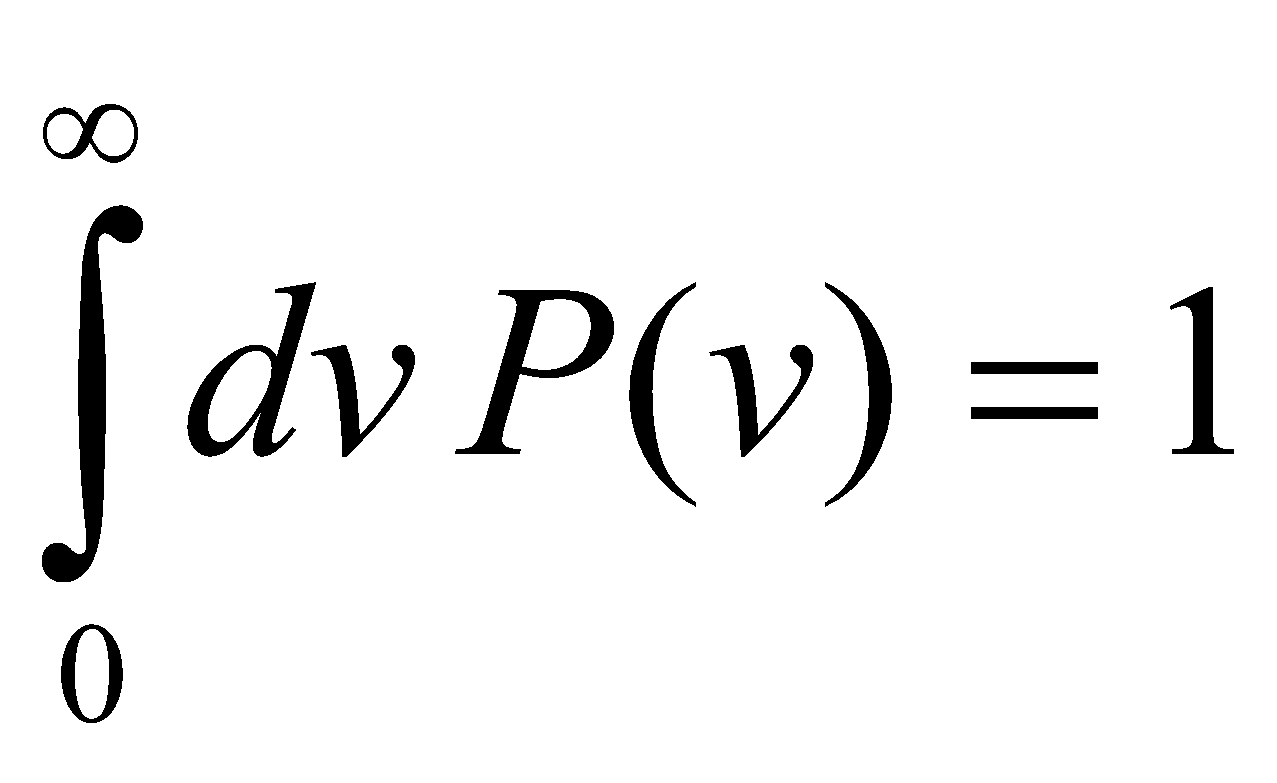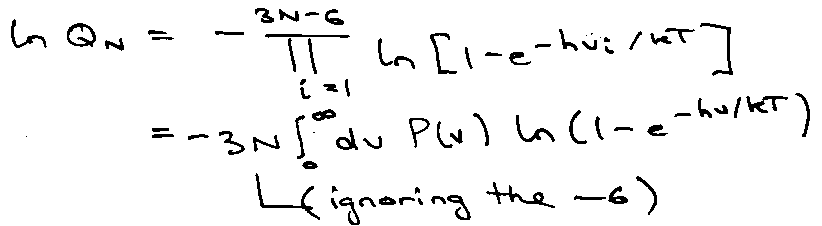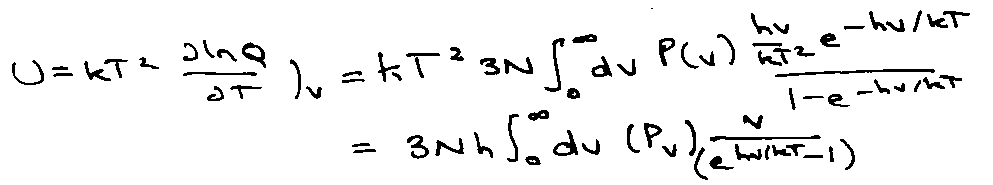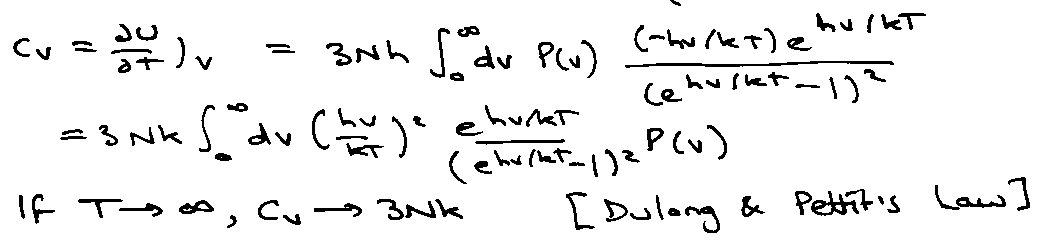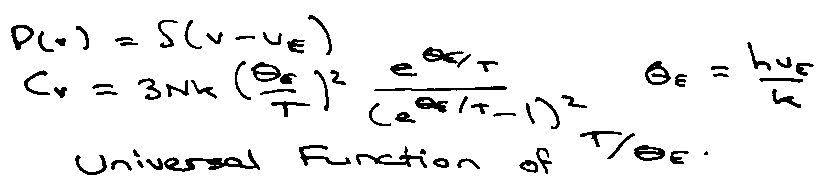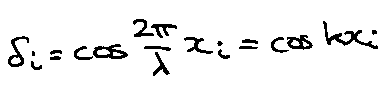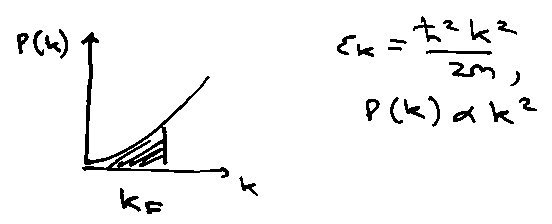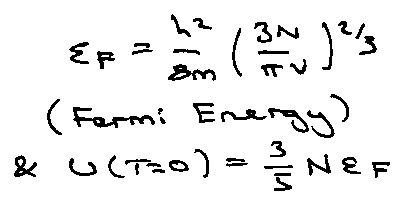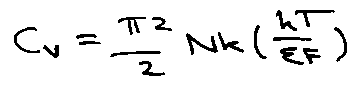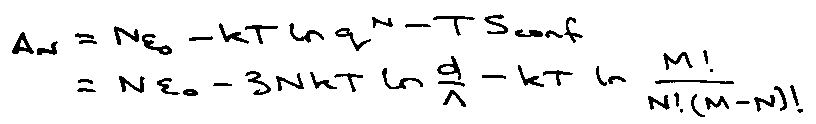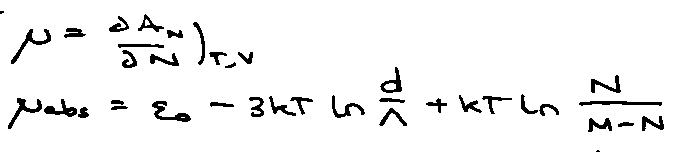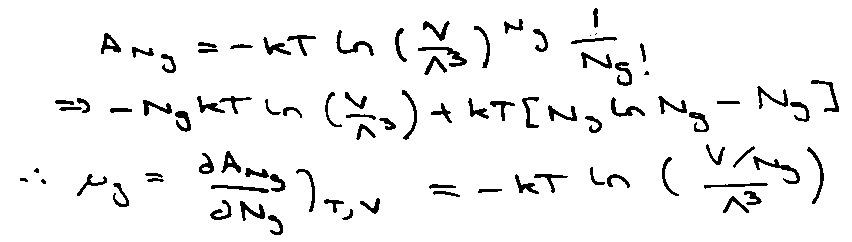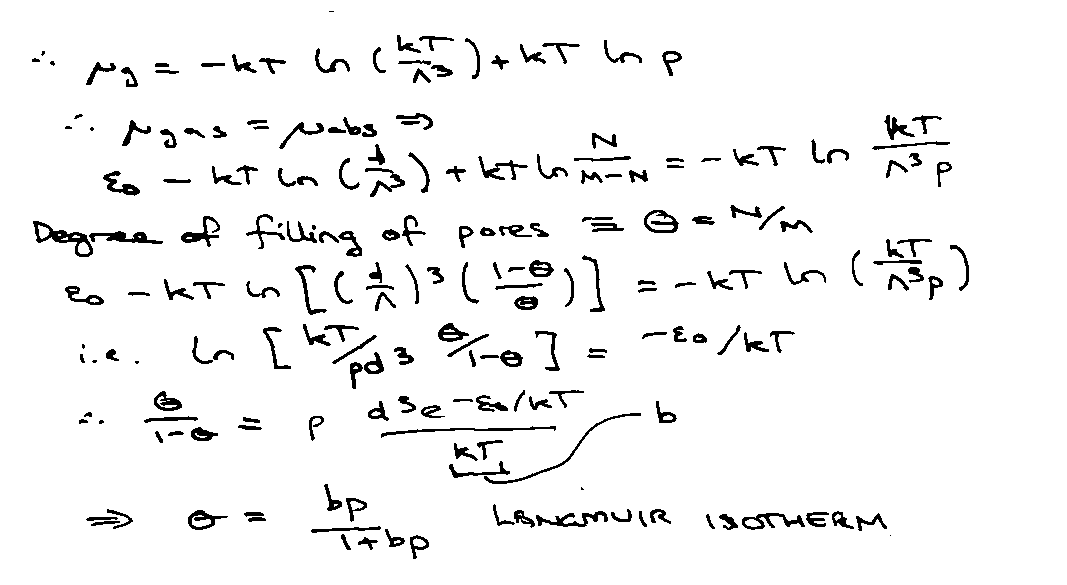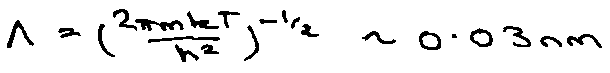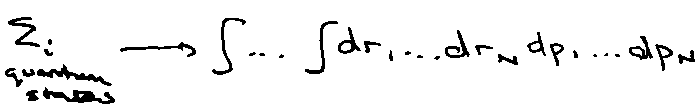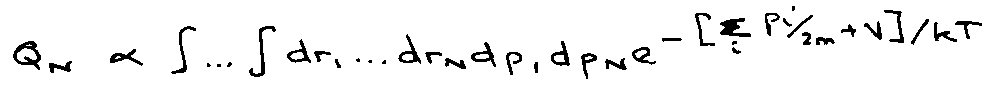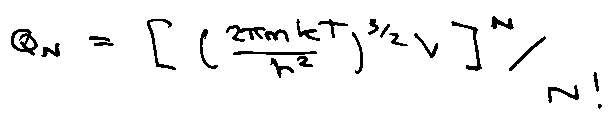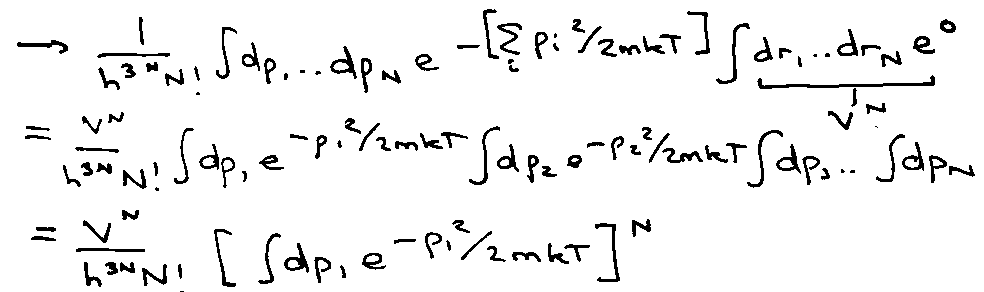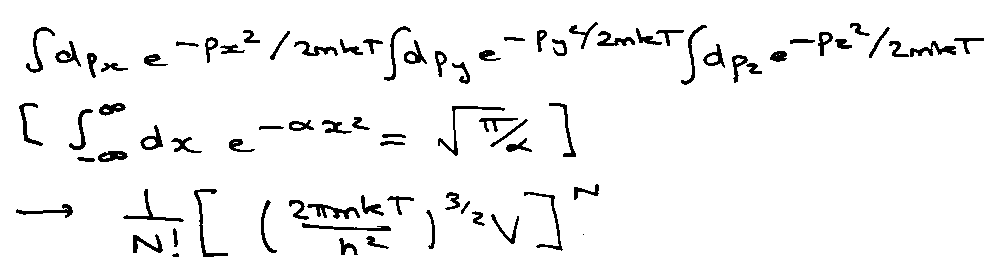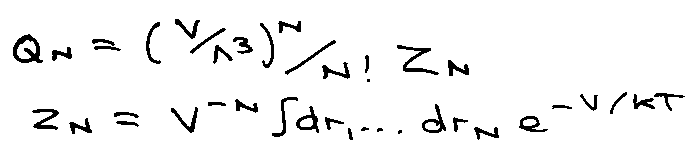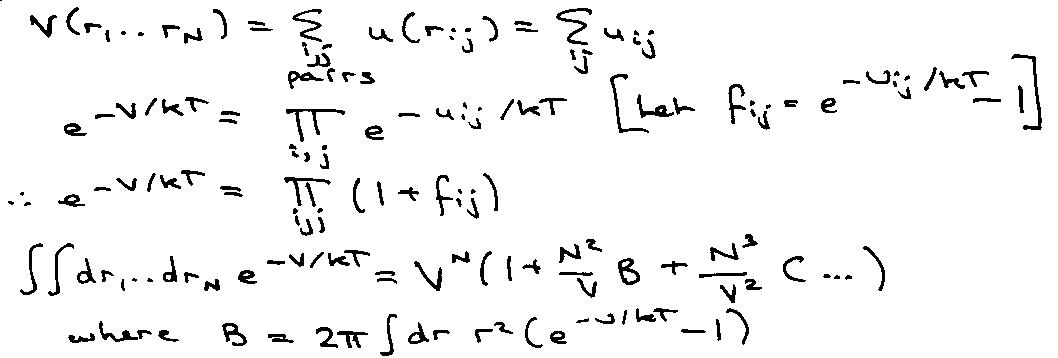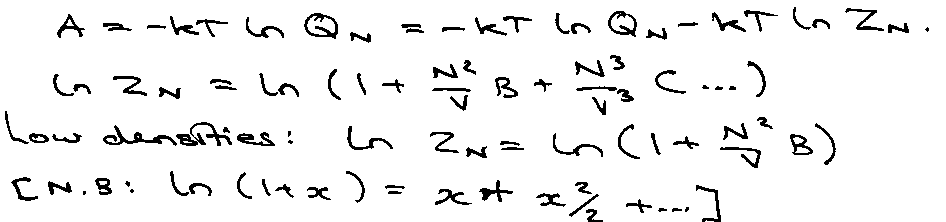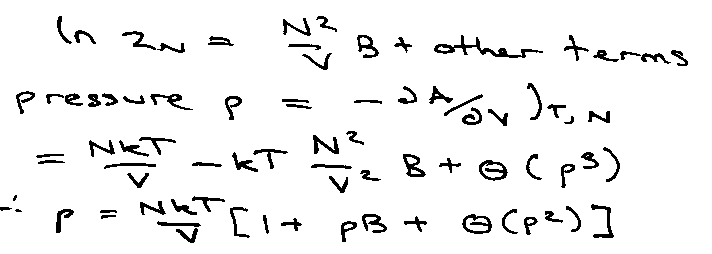Applications of Statistical Mechanics Notes

Statistical Mechanics links Energy-Levels (Quantum) to Macroscopic Properties (Thermodynamics).

Partition Function

For N molecules in volume V and temperature T,

Helmholtz Free Energy:

AN = -kT ln QN

Links to other thermodynamic quantities using this relation.

dA = - pdV – SdT

Therefore,

Calculating the partition function much simpler if can divide into non-interacting parts (e.g. independent molecules).

Total Energy, Ei = εi,1 + εi,2 + … εi,N

Therefore,

If molecules are identical and indistinguishable:

QN = qN/N!

But QN = qN if e.g. on lattice sites.

Molecular Partition Function (Revision)

Translation:

Rotation:

At high T: (kT > 2Bhc)                [ ~ 15K for HCl where B ~ 10cm-1 ]

qrot = kT/σBhc

where σ = symmetry number.

More generally for 3 moments of inertia (A,B,C):

Vibration:

Electronic:

2-Level Non-interacting System

e.g. lattice of immobile molecules with low-lying electronic energy levels.

e.g. crystal of NO        [ Ground State 2Π1/2 with low-lying 2Π3/2 ]

QN = qN

Both are 2-fold degenerate,

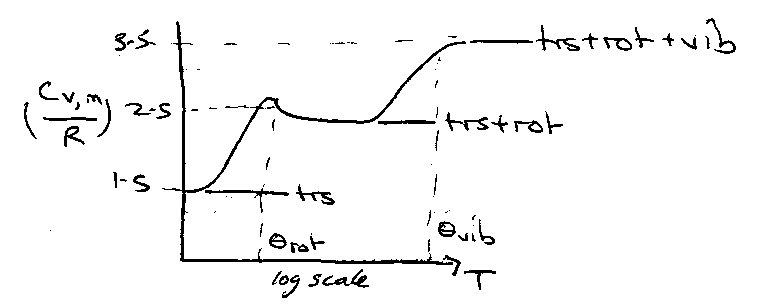
Heat Capacities of Gases

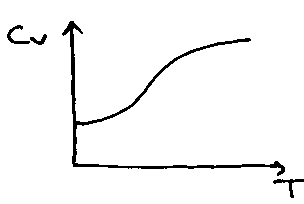
Heat Capacity as a Function of T:

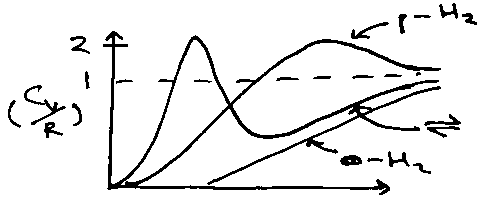
Little maximum present in Crot due to isolation of the bottom two levels at low temperature. High T → Ground → 1st → 2nd …

(also degeneracies).

qtr:

qrot:

Transition Regime → kT ~< Bhc –

Need full qrot:

Let T* = kT/Bhc

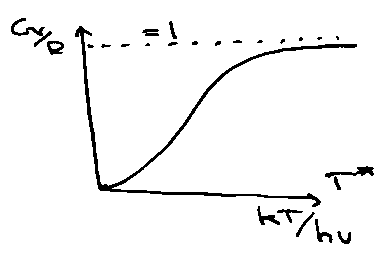
i.e. Cvrot for different diatomic systems is identical if plotted versus T*, the reduced temperature.

Nuclear Spin Effects (identical nuclei)

Implies only odd J allowed, i.e. half the states are missing, consistent with:

qrothomo = qrothetero / 2

H2:

Can interpret the behaviour from the two-level system results:

Para:         g1/go = 5, at kT ~ 0.3 x 6Bhc, Cvmax ~ 1.5R.

Ortho:         g1/go = 7/3, at kT ~ 0.35 x 10Bhc, Cvmax ~ 0.8R.

Equilibrium, go = 1, g1 = 3 x 3, so g1/go = 9, kT ~ 0.25 x 2Bhc, Cvmax = 2R.

qvib:

Since E-levels equally spaced, can’t use 2-level system results.

At high T, qvib → kT/hv, i.e. Cv → R x no. of normal modes.

Can thus measure vibration spectrum from the heat capacity.

The form of the Universal Function is:

EXAMPLES:

Absolute Gas-Phase Entropies

Thermodynamics:

Calorimetric Entropy.

Area under Graph of Cp vs. T.

Statistical Mechanics:

Spectroscopic Entropy

Difference in the calorimetric and spectroscopic entropies: Sresid = Sspec – Scal.

Sresid ≠ 0 → complications!

• Undetected low temperature phase transition.
• Use of wrong low-T degeneracy.
• Disorder in the crystal at low T, such that So > 0.

Gas:

→ trans, rot, vib, etc give additive contributions.

Monatomic Gas:

NOTE: Substances only distinguished by mass (at same T), and Smo = constant + R ln m3/2.

Rotational Entropy –

Linear diatomic – kT > Bhc.

qrot = kT/σBhc

NOTE: The role of symmetry number (CO = 214 while N2O = 220 despite similar m & I).

Vibrational Entropy –

If kT << hv, qvib → 1 and Svib = 0.

Generally,

Svib =

Electronic Entropy –

Only important for degenerate g-states, e.g. O2 – go = 3, or low-lying states, e.g. NO.

Verification of the 3rd Law –

Compare Calorimetric (assuming Smo (0) = 0) and spectroscopic entropies.

Statistical:

Thermodynamic:

But for N2O:

If random orientations → R ln 2 ( = 5.8 J K-1 mol-1)

Transition to fully ordered state occurs at such low temperature (due to very small ΔH from ordering) that kinetics so slow that transition is not seen.

Chemical Equilibrium

Kp = e-ΔG/RT

i.e. the different of molar Gibbs Energies at T of interest where p = po.

Link to statistical mechanics:

G = A + pV.

Gm = A + RT (non-interacting).

Gm = - kT ln (qN/N!) + RT

Using Stirling’s Approximation:

- kT [ N ln q – N ln N + N ] + RT

Illustration – isotope exchange reaction –

H2 + D2 ⇌ 2HD

T = 1000K, vH2 = 4400cm-1

Establish common energy zero by atomising reactants and products.

Ratio of Partition Functions –

qel = 1 for all.

Often high degree of cancellation when moles on left hand side of reaction equation equal the moles on the right hand side.

All factors cancel from this except masses.

All cancel except μ and σ 

Total gives:

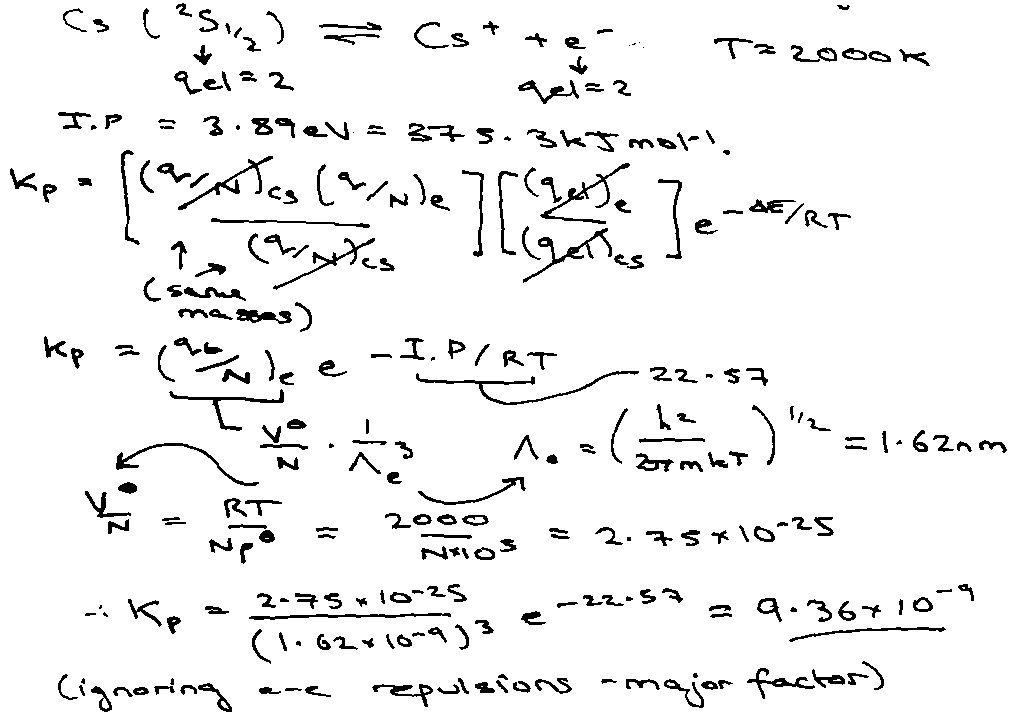
Illustration 2 – Thermal Ionisation

Fraction of ionised Cs atoms at p/po = 10-4.

Statistical Mechanics expression for Kc:

Transition State Theory

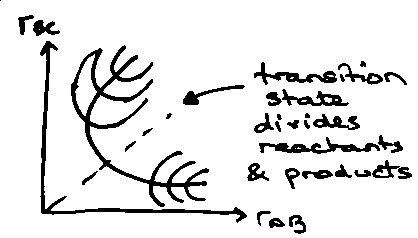
A + BC → AB + C

Profile:

Quasi-Equilibrium Assumption:

Kc because equilibrium in concentration.

ks = rate of passing through transition state = a velocity.

Alternatively, can think of vibrational motion along s.

Asymmetric stretching frequency v – assume transition state breaks up each time bond is stretched, i.e. ks = v.

Kc‡ includes vibrational and rotational partition functions of ‡, but factor qvib for asymmetric stretch. Therefore,

Since v very low (weak bond) → kT/hv. Therefore,

Check that Transition State Theory gives same rate constant as Simple Collision Theory when applied to collision of structureless spheres:

Transition State Rate Constant for:

H + H2 → H2 + H @ 1000K.

Experimental of ~ 109 at these temperatures (accuracy in barrier height).

Interacting Systems

So far, have written QN = qN.

But for e.g. atomic solid cannot write E =

Implies must effect a transformation to new variables which do not interact.

e.g. thermal properties of an insulating crystal.

Crystal is harmonic, i.e. for small displacements E is proportional to (δri)2.

Transform from atomic to normal coordinates (normal modes) – phonons.

Each modes has a frequency vi and is independent of degree of excitation of other modes,

Since N ~ NA, spectrum is dense and continuous. Let P(v) be probability of finding mode frequency v [

Internal Energy (wrt ZPE) –

Heat Capacity –

But Cv only 5.4J K-1 for diamond at 298K (one of “failures of classical physics”).

Einstein’s Theory of Heat Capacity

Data appears to be Universal but functional form is not correct. Einstein → exponential at low T.

DeBye Model

Improved the model of vibrational spectrum. Normal modes characterised by the wavelength λ.

1. For small k (large λ) behaves like a continuum (v = c/λ = ck/2π).
2. Cut-off wavevector, k = π/a (λ = 2a) – zone boundary.
3. P(v)? Consider chain, length L

So for low T, Cv T3.

[ Integrand → 0 for x << xmax → integral is T-dependent ].

Heat Capacity of Metals

Cv for metals looks DeBye-like. What about free electrons?

Free Electron Model – e-e interactions screen e-ion interaction. Electrons move independently in a smeared out 3D particle-in-a-box like-potential.

Energy Levels are filled according to the Aufbau Principle.

At T = 0, highest occupied level is:

NB: Huge contribution to pressure balanced by electron-ion interaction.

Only a few electrons near to εF can be excited thermally. Distribution described by Fermi-Dirac (not Boltzmann).

Therefore negligible except for very low T (all other contributions → 0).

Absorption of Gas in a Porous Material

Example of Phase Equilibrium.

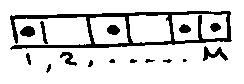
Consider N immobile atoms absorbed in M sites.

With no 2 atoms in a single site – allows for interatomic repulsion.

Number of configurations = M(M-1) … (M-N-1). = M!/(M-N)!

But it atoms indistinguishable = M!/(M-N)!N!

Therefore neglect atom motion:

Sconf = k ln [M!/(M-N)!N!]

Each pore is of side d. Absorption energy εo. Model motion of absorbed atom as translation in volume V = d3.

Partition Function = d3/Λ3 = q.

Provided box is big enough that quantum effects not important,

Δε ~ h2/8md2.

Therefore the Helmholtz Free Energy:

Absorbed atoms in equilibrium with gas at pressure p when μabs = μgas.

For Ng gas-phase molecules,

Also, pV = NgkT.

Provides a microscopic interpretation for the empirical parameter b.

Classical Interacting Systems (fluid)

For most liquids, can treat system classically, e.g. for Ar at 84K (triple point):

i.e. thermal de Broglie wavelength << interatomic separation, therefore classical.

How do we get a classical partition function? Expressed in terms of particle positions and momenta. A point in “phase-space” is specified by all molecular positions and momenta.

R, P = [ r1, r2, … rN ; p1, p2 … pN ]

Expect,

Energy at R, P = H(R,P) and probability of being at R, P:

What is constant –

1. Need 1/N!                 (indistinguishability)
2. ΔxiΔpi ≥ h                (HUcP)

i.e. each point in phase-space only distinguishable from another if drdp > h.

Therefore overall need 1/h3N factor.

Check, do we get same value as classical limit of quantum partition function.

e.g. ideal gas (quantum):

Classically V → 0:

Integral is:

Generally,

Application: Low Density Interacting Gas (Virial)

Suppose atoms of a gas interact via a pair potential:

Consider,

i.e. Virial Expansion, B is the Virial Coefficient.